计及噪声激励的模态参数识别方法
2018-07-05夏遵平
夏遵平, 王 彤
(南京航空航天大学机械结构力学及控制国家重点实验室,江苏 南京,210016)
引 言
振动模态参数识别被广泛应用于结构动态分析领域,如航空航天、大型船舶、高速列车及其他重型装备的研制与生产、大型桥梁的验收与监测等,是结构产品从动态设计到生产和维护过程中不可或缺的技术[1-3]。一般可将基于测试的模态参数识别方法归纳为二大类[4]:一是基于结构激励和响应的传统试验模态分析(Experimental Modal Analysis,EMA)法[5];二是仅基于结构响应的运行模态分析(Operational Modal Analysis,OMA)法[6-7]。EMA方法虽然参数识别的可靠性较高,但通常需要机械结构处于非工作状态和较小噪声环境中测得激励与响应数据[8-9]。OMA方法不需要测得系统的输入数据,利用机械结构自身运行或周围环境噪声激励下的响应数据识别结构模态参数[10]。但OMA方法依然存在一些不足,如:由于采用自然激振,不能控制激振力的频谱成分和施加位置,可能导致某些模态不能被很好地测试出来,存在模态遗漏的风险[11];激振力无法测得,没有很好的办法对模态振型进行归一化。
近年来,一种机械结构工作状态下的试验模态测试技术逐渐发展起来。例如,飞机飞行颤振试验中,除未知的气动力激励外,再施加可测的舵面激励[12],将EMA方法与OMA方法结合起来,形成了含已知激励的运行模态分析(Operational Modal Analysis in presence of eXogenous inputs,OMAX)法[13]。该方法被认为结合了EMA和OMA优点,既可识别出机械结构真实工作状态下的模态参数,又可弥补OMA方法可靠性差的缺陷。目前,一种实现OMAX的方法是基于频响函数(Frequency Response Function, FRF)和噪声响应的半功率谱密度(Half Power Spectral Density,HPSD)函数[14]来识别结构模态参数。该方法通过获取功率谱密度(Power Spectral Density,PSD)函数的正频率部分,使得到的HPSD函数与FRF函数具有相同的极点数,认为两者可以融合。OMAX的另一类实现方法是基于FRF和传递率函数(Transmissibility Function,TF)[15]来识别结构模态参数,该方法试图通过计算各点响应PSD比值之差的倒数来构造可以与FRF融合的函数。目前研究表明,该法虚假极点较多,有时阻尼比和振型识别容易失效[4, 16]。
本文提出一种计及噪声激励的试验模态分析(Experimental Modal Analysis with consideration of noise eXcitation, EMAX)方法。根据含噪声激励的无参数模型估计出仅含噪声响应的功率谱函数,并对其进行Hilbert变换估计出噪声响应的类频响函数(Analogous FRF,AFRF)。研究表明,AFRF具有与传统FRF一致的系统极点和相似的数学表达[17-18],可以与FRF融合,采用EMA方法识别出模态参数[19]。以弯扭二自由度机翼的数值仿真和GARTEUR飞机模型试验为例,分析所提AFRF的性质。通过与仅EMA法、仅OMA法和OMAX法对比,验证本文方法的可靠性和有效性。
1 理论背景
1.1 类频响函数估计
结构系统同时含有已知激励和未知激励的输入-输出模型如图1所示。

图1 含未知激励的输入-输出模型Fig.1 Input-output model with ambient excitation
图中,fk和yk分别表示可测激励及其产生的系统响应,fu和yu分别表示不可测激励及其产生的系统响应,y表示测得的系统的响应。H′和H″分别表示可测力与不可测力对应的频响函数,可能只是总体FRF的一个元素或一行或一列。上述各变量的频谱关系可表示为
Y=Yk+Yu=H′Fk+H″Fu
(1)
式中Y,Yk,Yu,Fk和Fu分别为y,Yk,yu,fk及fu的傅里叶变换,且只有Y和Fk已知(试验测得)。根据上式,未知响应可表示为
Yu=Y-H′Fk
(2)
则得到其功率谱函数为
(3)
式中 上标H表示复数矩阵的共轭转置,Sff和Syy分别表示测得的激励与响应的自功率谱,而Syf表示测得的响应与激励的互功率谱。对于响应中含噪声的情况,公式(3)中的频响函数可采用H1估计[20]方法获得,即
(4)
将式(4)代入公式(3)得到基于输入输出的噪声响应功率谱函数为
(5)
由于频响函数的相位与幅值存在Hilbert变换的对应关系[15-16],进而可得到原点频响函数的真实相位与该点响应自谱的关系为
(6)
式中 H为Hilbert变换符号。得到未知激励下的原点AFRF为
(7)
同时注意到,第i点激励、第j点响应的跨点与原点AFRF的关系为
(8)
(9)
式中 上标T,H及*分别表示转置、共轭转置及共轭;Nr为系统的极点数;r为系统极点的阶次;Φr为第r阶振型;Kr为第r阶模态参与向量或含有比例常数的模态参与向量;λr为系统的第r阶极点。
1.2 参数识别
(10)
式中Ωr=exp(-jωrΔt)为多项式基本项,r为模型阶次,αr和βr为参数向量。设αr和βr的集合为
θr=[αrβr]T
(11)

(12)
式中Wo(ωk)为加权函数。Xo和Yo分别为:
(13)
(14)
式中 ⊗表示Kronecker乘法。
对公式(12)求平方和并取其实部的迹,得
(15)
式中 Re(·)表示取实部,上标H表示共轭转置。参数向量α可由最小二乘解出,然后求得其伴随矩阵的特征值为
(16)
式中Λ即为系统的极点组成的对角矩阵,据此可求出系统的固有频率和阻尼比;V为参与向量,据此便可求出振型。
(17)

2 算例分析
2.1 仿真算例
图2所示的弯扭二自由度机翼模型被广泛应用于飞机飞行颤振分析的仿真验证。该模型的平动和转动可模拟真实机翼的弯曲和扭转两种振动模态。设机翼质量m=5 kg,转动惯量JG=3.34 kg·m2,平动弹簧刚度为k1=3.6×104N/m,转动弹簧刚度为kr=2.0×104N/m;偏心距e= 0.05 m,两测点分别位于l1=0.8 m,l2=1 m;两阶模态分别加入阻尼比为1.2%和0.86%的结构阻尼。在图中的1号点和2号点处施加随机噪声激励,同时在1号点处施加0~40 Hz的线性扫频激振。设扫频激励和仿真响应的采样率为102.4 Hz,采样时间为800 s,得到时域激励与响应如图3所示。根据上节中的Hilbert变换理论,估计出未知噪声激励下的AFRF,并将其与理论FRF比较,如图4所示。

图2 机翼物理模型Fig.2 The physical model of the aircraft wing

图3 时域激励与响应(局部)Fig.3 Input and output signal (zoom in)
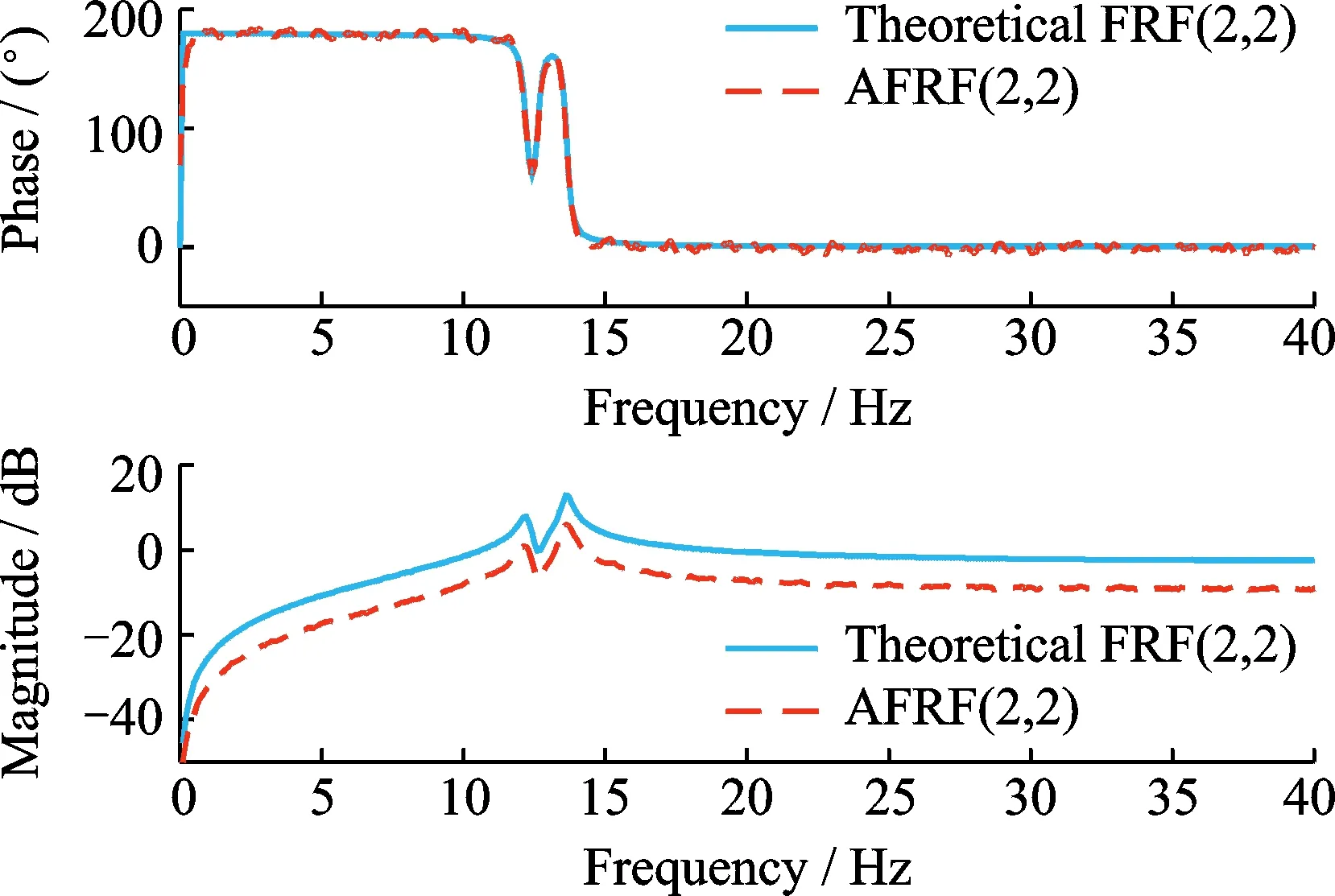
图4 理论频响函数与类频响函数Fig.4 The theoretical FRF and analogous FRF
由图4可知,根据公式(7)和(8)估计出的噪声激励的AFRF与理论FRF具有相同的相位,且两者的幅频曲线也保持着一致性,仅相当于在数值上相差一个比例常数。因此,可认为仅根据噪声响应功率谱估计出的AFRF与理论FRF有相同的性质及相似的表达形式。分别基于EMA (仅FRF)法[5,19]、OMA (仅HPSD)法[19]、OMAX (FRF+HPSD)法[13-14]和本文提出的EMAX法识别出结构的模态频率与阻尼比,如表1和2所示。
表中结果表明,在本算例中,各方法识别出的固有频率均具有较小的相对误差,而前3种传统方法对阻尼比的识别误差较大。这是因为阻尼参数比固有频率参数更为敏感,易受信噪比、测试的完备性等因素影响。由误差对比可知,EMAX方法识别参数的精度明显高于其他方法。这是因为与EMA方法相比,EMAX方法采用噪声响应扩充了频响函数,使其更完备;与HPSD函数相比,基于Hilbert变换的AFRF不仅具有相同的极点数,零点-极点的组成也近似(曲线形状相似)。各方法计算过程中的稳态图如图5所示,图中曲线为复模态指示因子曲线。其中,EMA方法由于人工激励的不完备,仅能得到一列频响函数,即仅有一条复模态指示因子曲线。
尽管我国“保基本、强基层、建机制”的医疗体制改革已使基层医疗卫生机构硬件设施明显改善,但是,国家卫计委发布的公报显示,2015年,全国医疗卫生机构总诊疗人次达77.0亿人次。其中,三级医院的诊疗人次和入院人数增长分别为7.14%和8.55%,而基层医疗卫生机构出现了负增长,增长率分别为-0.46%和-1.39%[11]。

表1 估计出的固有频率比及相对误差

表2 估计出的模态阻尼比及相对误差

图5 模态稳定图Fig.5 Modal stabilization diagrams
2.2 实 验
如图6所示的GARTEUR (Group of Aeronautical Research and Technology in EURope)飞机模型是欧洲航空科技研究集团于20世纪90年代中期设计制造的。该模型具有真实飞机的主要振动模态特征,因此,在航空界得到广泛应用。

图6 实验装置Fig.6 Experimental setup
将基于GARTEUR的振动测试分成两组:第一组,作为参考,在无噪声激励的情况下,利用脉冲激励测得加速度FRF;第二组,在脉冲激励的同时,用激振器模拟环境噪声激励。测试过程中采样频率均设为128 Hz,每个测点实施8次锤击脉冲激励,每次脉冲触发采样时间为16 s(即频率分辨为0.0625 Hz),得到典型的加速度响应信号如图7所示。

图7 响应信号Fig.7 Output signals
由公式(6)~(8)估计出测得的噪声响应的类频响函数,并将其与真实频响函数对比,如图8所示。由图中两种曲线对比可知,AFRF的相位与真实FRF的相位一致(部分频段相位相反),并且注意到两者的幅频曲线形状也相似,即在数值上仅相差一个比例常数。基于第一组实验数据,采用多参考点的最小二乘复频域法(polyLSCF)[19]识别出的模态参数作为参考值,其计算稳态图如图9所示;基于第二组实验数据,分别采用EMA法、OMA法、OMAX法和EMAX法识别出结构50 Hz内的结构模态频率(如表3所示)和阻尼比(如表4所示),各方法的计算稳态图如图10所示。

图8 GARTEUR模型的频响函数与类频响函数Fig.8 The FRF and AFRF of GARTEUR

图9 PolyLSCF识别的稳态图(基于第一组测试数据)Fig.9 Stabilization chart of polyLSCF(based on the first test data)

参考频率/Hz(第一组实验)EMA方法/Hz相对误差%OMA方法/Hz相对误差/%OMAX法/Hz相对误差/%EMAX方法/Hz相对误差/%6.126.120.006.120.006.120.006.130.1616.1216.11-0.0616.09-0.1916.11-0.0616.11-0.0635.7435.740.0035.740.0035.73-0.0335.750.0339.5539.550.0039.550.0039.550.0039.550.0039.94--39.940.00--39.93-0.0347.2347.21-0.0447.230.0047.240.0247.20-0.0648.3848.420.0848.390.0248.410.0648.40-0.08

表4 估计出的模态阻尼比及相对误差
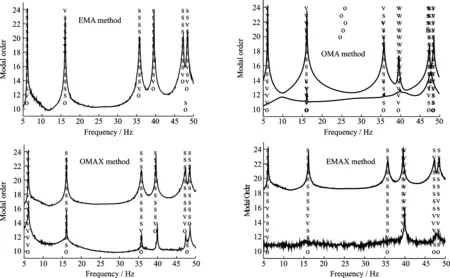
图10 4种参数识别方法的稳态图(基于第二组测试数据)Fig.10 Stabilization charts of four methods (based on the second test data)
对比表3和4中的参数识别结果发现,由于施加的人工激励不完备,使得激励出的第5阶模态较弱,同时基于HPSD的OMAX方法并未有效改善这一问题,进而导致EMA法和OMAX法仅识别出了6阶模态参数,漏掉了第5阶模态。此外,注意到OMA方法和OMAX方法识别出的阻尼比误差较大,这是由于相比于频率,阻尼参数更为敏感,对识别方法、测试数据质量等有较高要求,而本实验的响应数据中含有脉冲和随机两种不同属性的成分,而且数据长度有限,因而影响上述方法对模态阻尼比的识别精度。与之相比,EMAX法不仅识别出了全部的结构模态,而且提高了模态阻尼比的识别精度。EMAX法识别出的50 Hz内的模态振型如图11(a)~(g)所示。

图11 识别出的模态振型及其MAC值Fig.11 Estimated mode shapes and MAC values
图11(h)为振型与参考振型的模态置信准则(Modal Assurance Criterion,MAC)矩阵,其对角值均接近于1,非对角值均小于0.3,说明两者具有较好的匹配度,即采用EMAX方法识别出的振型是可靠的。综上结果表明,本文提出的EMAX方法是有效且可靠的。
3 结 论
(1)基于噪声响应估计出的类频响函数与真实频响函数具有相同的性质,当噪声激励的频域特性满足平直谱时,两者仅相差一个常数,因而更适于联合。
(2)与OMAX方法依据OMA理论不同,本文提出的参数识别方法立足于EMA,利用结构自身工作或周围环境激励,弥补由于人工激励不完备而可能存在的问题。
(3)该方法可用于机械设备的工作状态或桥梁的交通状态的试验模态分析,测试过程中实施较少的人工激励也能得到较可靠的数据,节省了试验成本。
需要说明的是,本文中基于功率谱Hilbert变换的类频响函数的推导要求环境或结构工作提供的噪声激励近似满足随机分布。对于多数模态测试情况,考虑较窄的识别频带,这种近似条件是合理的。
[1] Reynders E. System identification methods for (operational) modal analysis: Review and comparison [J]. Archives of Computational Methods in Engineering, 2012, 19(1): 51—124.
[2] Pintelon R, Schoukens J. Vandersteen G, Frequency domain system identification using arbitrary signals [J]. IEEE Transactions Automatic Control, 1997, 42(12): 1717—1720.
[3] Cheung Y K, Leung A Y T. Finite Element Methods in Dynamics [M]. Kluwer Academic Publishers, Dordrecht, 1991.
[4] Wang T, Celik O, Catbas F N. Damage detection of a bridge model based on operational dynamic strain measurements [J]. Advances in Structural Engineering, 2016, 19(9): 1379—1389.
[5] Verboven P, Cauberghe B, Guillaume P. Improved total least squares estimators for modal analysis [J]. Computers and Structures, 2005, 83: 2077—2085.
[6] Brincker R,Zhang L M, Anderson P. Modal identification from ambient response using frequency domain decomposition[C]. Proceeding of the 18th IMAC, 2000:625—630.
[7] Reynders E, Maes K, Lombaert G, et al. Uncertainty quantification in operational modal analysis with stochastic subspace identification: validation and applications [J]. Mechanical Systems and Signal Processing, 2016, 66-67: 13—30.
[8] 孙鑫晖, 郝木明, 李振涛, 等. CMIF方法中模态参数不确定性的计算[J]. 振动工程学报, 2013, 26(3): 380—386.
Sun X H, Hao M M, Li Z T, et al. Uncertainty calculation in complex modal indictor function identification method [J]. Journal of Vibration Engineering, 2013, 26(3): 380—386.
[9] 王 彤, 张令弥. 多频段拟合的正交多项式方法及其Matlab工具箱[J]. 振动工程学报, 2003, 16(4):493—497.
Wang T, Zhang L M. FA Multiple frequency band fitting method using orthogonal polynomials and corresponding matlab toolbox [J]. Journal of Vibration Engineering, 2003, 16(4): 493—497.
[10] Schoukens J, Pintelon R. Measurement of frequency response functions in noisy environments [J]. IEEE Transactions on Instrumentation and Measurement 1990, 6(6): 373—377.
[11] Brinker R, Ventura C E. Introduction to Operational Modal Analysis [M]. John Wiley & Sons Ltd., 2015, 10—11.
[12] Zhang L M, Brincker R, Andersen P. An overview of operational modal analysis: major development and issues[C]. Proceedings of the 22nd International Modal Analysis Conference, 2004: 179—190.
[13] Vanlanduit S, Guillaume P, Cauberghe B,et al. On-line identification of operational loads using exogenous inputs [J]. Journal of Sound and Vibration, 2005, 285(1-2): 267—279.
[14] Troyer T D, Runacres M. Frequency-domain modal analysis in the OMAX framework[C]. Proceedings of the 28th International Modal Analysis Conference, Jacksonville, Florida USA, February, 2010: 465—476.
[15] Devriendt C, Troyer T D, Sitter G D, et al. Transmissibility-based operational modal analysis for flight flutter testing using exogenous inputs[J]. Shock and Vibration, 2012, 19(5): 1071—1083.
[16] 张永年. 基于传递率函数的运行状态模态分析方法及软件实现[D]. 南京: 南京航空航天大学,2014.
Zhang Y N. Transmissibility-based operational modal analysis and software implementation [D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014.
[17] Agneni A, Crema L B, Coppotelli G. Output-only analysis of structures with closely spaced poles [J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1240—1249.
[18] 夏遵平, 王 彤, 张永年. 基于Hilbert谱变换函数的运行模态分析方法[J]. 地震工程与工程振动, 2014, 34(6): 97—102.
Xia Z P, Wang T, Zhang Y N. Operational modal analysis based on hilbert transformation [J]. Earthquake Engineering and Engineering Dynamics, 2014, 34(6): 97—102.
[19] Peeters P, Van Der Auweraer H, Guillaume P, et al. The PolyMAX frequency-domain method: a new standard for modal parameter estimation [J]. Shock and Vibration, 2004, 11(3-4): 395—409.
