多孔壁面槽道湍流中的流动阻力和传热

张一凡,刘财喜,董宇红

(上海大学上海市应用数学和力学研究所,上海200072)

多孔介质是自然界和工业领域中普遍存在的一种物质,其内部具有大量相互贯通的、向外敞开的微孔,具有较大的比表面积、吸附容量等特征.作为一种多功能的材料,多孔介质可实现诸如过滤、分离、吸附、吸声、热传输和调节流动等功能[1].由于具备这些特性和功能,使得其具有较强的应用性,故对多孔介质中流体流动及传热传质的研究在工农业生产领域具有非常广阔的应用前景.例如,随着人类社会对自然资源需求的日益增加,日益减少的自然资源使得对地下资源,如石油、天然气等的开发利用难度加大,因此当务之急是提高油藏采收率,以及加大天然气在惰性多孔基质中的提取.在更广泛的意义上,多孔介质的研究涉及到流体和传热科学、材料、化学、地热、石油和燃烧工程等,如流化床燃烧、地下化学废物的扩散、化学催化反应器等.为了解决这些工程问题,需要对多孔介质中流体流动及传热等方面展开深入研究.

对于多孔介质的理论研究历史悠久,最早的研究是在1856年,法国人Darcy Herry经过长期实验总结出了水在砂土颗粒的间隙中流动的规律,发现渗透速度与水力坡度成线性关系,即著名的Darcy定律.Darcy定律奠定了渗流计算理论的基础,随后渗流力学研究取得了较大进展.1889年,茹可夫斯基首先推导出了渗流的微分方程;1922年,巴蒲洛夫斯基提出了求解流场的电模拟法,为解决比较复杂的渗流问题提供了一个有效工具,并由电模拟法逐步发展到电网模拟法;1931年,Richards[2]将Darcy的线性渗流理论推广应用到非饱和渗流中,并建立了Richards水流控制方程;随后Fredlund[3]基于Richards控制方程,将渗流进行更深入的研究,并成功应用到许多实际工程中.

经过不断的探索和发展,目前解决多孔介质中的流体流动问题主要有如下3类方法.

(1)直接模拟方法.在这种方法中多孔介质内部的每一个复杂几何尺度都被考虑[4].该方法结果精确,但计算量大.

(2)模拟边界条件法.通过设置边界条件来模拟多孔介质界面对流体的影响[5],这种方法适用于边界与流场之间作用关系确定、信息详细的环境中.

(3)宏观流动模型法.引入“容积平均”的概念,把多孔介质看作为一种在大尺度上均匀分布的虚拟连续介质[6].如今研究人员大多引用“容积平均”的概念对实际工程应用进行模拟,并通过对控制方程进行修正,添加作用力项来模拟多孔介质中流动[7-9].

多孔介质中传热现象普通存在于地球物理和工业生产的各个领域,如多孔固体干燥、保温、提高石油采收率等[10],已引起研究人员的高度重视.目前,最常用2种方法建立多孔介质渗流的热量方程[11].①局部热平衡法.认定多孔骨架的温度与对应点的流体温度相等,采用单能量模型进行模拟计算,如Alazmi等[12]在2000年对可渗透多孔介质和纯流体复合系统的传热研究中,在多孔介质区域的模拟计算中采用了局部热平衡法.②非热平衡法.认定多孔骨架的温度与任何对应点的流体温度不相等,采用宏观2个能量模型来模拟多孔介质骨架和其中的流体,如Saito等[13]在2010年对高孔隙率的多孔介质渗流模型中的流动和传热进行了模拟,其热场部分就采用了宏观2个能量模型分别对多孔介质骨架和流体进行了模拟.

近年来,研究人员对丰富多样的含有多孔介质壁面的模型进行了深入的探讨和研究.2002年,Hahn等[14]对含有多孔墙体的槽道湍流进行了模拟研究,发现多孔介质削弱了湍流强度,速度脉动和雷诺应力也都有所减弱,产生了一定的减阻效应;2012年,Nimvari等[15]分别研究了2种多孔介质填充槽道湍流(中心填充和近壁区填充)的传热问题,发现当多孔介质层厚度及达西数改变时,热场统计信息与Nusselt数发生了明显的变化;Sueki等[16]和Naito等[17]分别从实验和数值模拟的角度对多孔壁面圆柱绕流问题进行研究,探讨了多孔介质壁面对流动和噪音方面的影响,发现多孔介质削弱了速度脉动和压力脉动,产生了一定的减阻效应.

含多孔壁面的剪切湍流问题一直广受关注,通过添加多孔介质壁面可以对流动阻力、噪声、传热等方面产生影响,在工程应用中意义较大.本工作针对该问题进行研究,选取经典槽道壁湍流模型,在壁面处加入多孔介质层,流场方面采用宏观流动模型,热场方面采用局部热平衡法对多孔介质壁面进行数值模拟,以多孔介质孔隙率、达西数等为控制参数,分析了在不同工况下流场和热场的数值结果,并研究了多孔介质壁面对槽道湍流流动和传热等方面的影响.

1 数值模拟

1.1 动量方程

本工作假设2个无穷大平板之间的槽道湍流模型在压力驱动下流动(见图1),其中x,y,z分别为流向、法向和展向坐标,H为半槽道宽度.在上下壁面内侧设置多孔介质层,其厚度δ=H/30.对应坐标轴(x,y,z)的速度分量用(u,v,w)或(u1,u2,u3)表示.本工作计算在定压力梯度下进行,计算域为2πH×2H×πH.

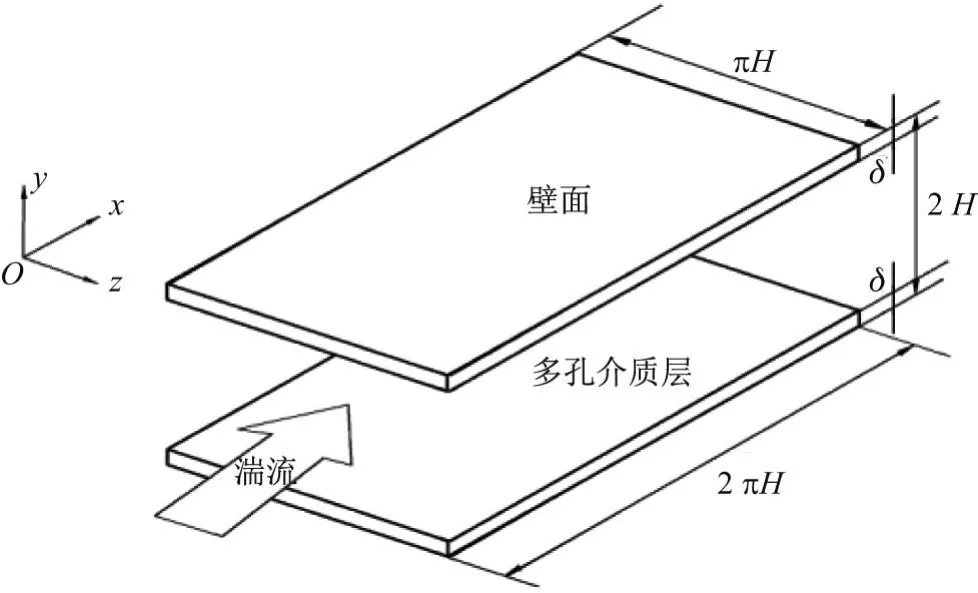
图1 多孔壁面湍流模型Fig.1 Sketch of porous wall-bounded channel f l ow

在对多孔壁面剪切湍流进行数值模拟时,需要对自由流体区域及多孔介质流动区域进行耦合.一些研究人员仍基于N-S方程与达西方程进行耦合来实现流动模拟,如Hahn等利用达西定律构造了适用于多孔结构与流体区域过渡层的界面条件,但是这种耦合处理往往比较困难.本工作采用Breugem等[18]提出的在N-S控制方程中引入体积平均化的概念描述多孔介质壁面对内部流动的影响,根据Nithiarasu等[19]修正的Brinkman-Forchheimer方程,设置多孔介质内部区域的流体运动控制方程:

式中,i,j为流体运动的方向;t为时间;p为压力;雷诺数Reτ=uτH/ν,在本工作中雷诺数Reτ=180;v为流体运动黏度;物理量均为无量纲,由壁面摩擦速度uτ和半槽道宽度H对控制方程进行无量纲化;壁面摩擦速度为壁面剪切应力;作用力F项为介质阻力[20],

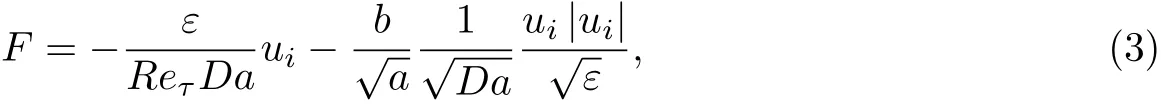
根据Ergun[21]的经验取a=150,b=1.75,用无量纲特征参数达西数Da=K/H2代替了渗透率K;ε为孔隙率.

1.2 能量方程

本工作假定多孔介质中流体和固体之间满足局部热平衡条件,那么多孔介质内热流动的控制方程除式(1)～(3)给出的质量和动量方程外,还包含如下能量方程:

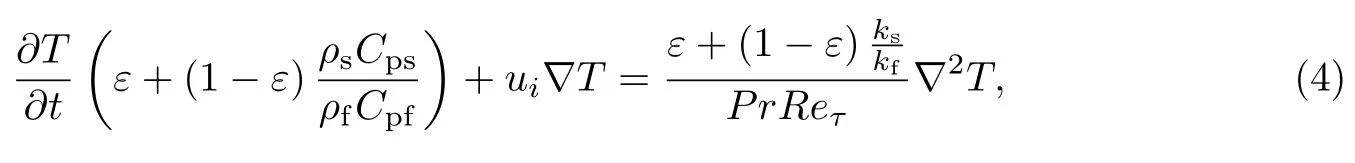
式中,T为温度,ρs和ρf分别代表固体和流体的物理密度,Cps和Cpf分别为固体和流体的定压比热,ks和kf为二者的导热系数,普朗特数Pr=ν/κ,在本工作中设Pr=0.71.

1.3 初边界条件

本工作在流场方面,流向和展向采用周期性边界条件,法向采用无穿透无滑移边界条件.

根据数值实验设定的研究目的不同[22],热场方面采取2种不同的温度边界条件:①上下壁面恒定温度值:y=−1,T=−0.5;y=1,T=0.5,初始温度场设置为T=y/2;②上下壁面恒定热通量:y=−1,∂T/∂y=2;y=1,∂T/∂y=−2,初始温度场设置为T=1−y2[23].

1.4 数值方法及验证

本工作选用容积平均作用力模型对多孔壁面槽道湍流进行数值模拟,流向和展向采用均匀网格,法向采用近壁区加密网格,壁面区域最小网格尺寸=0.425.本工作控制方程的离散基于交错网格,在时间离散上采用混合3步Runge-Kutta/Crank-Nicholson格式:①对流项的时间推进采用3阶精度的显式Runge-Kunta法;②粘性项采用2阶精度的隐式Crank-Nicholson格式;③在空间离散中采用2阶精度的中心差分格式.

为了验证上述离散方法在数值模拟中的有效性和程序的可靠性,本工作首先对无多孔材料的光滑壁面槽道湍流进行了直接数值模拟,分别选取网格数为65×129×65以及129×129×129,将结果与Kim等[24]的直接模拟结果及经Kim修正的Echelmann[25]实验结果进行比较,结果如图2所示.本工作2种分辨率的计算结果与Kim等的结果符合得较好,与Echelmann实验结果也比较接近,精度足以满足计算要求.

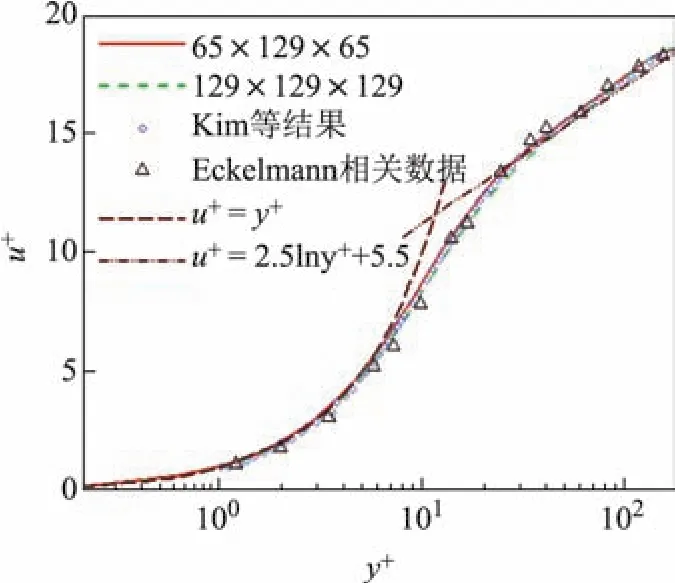
图2 流向平均速度Fig.2 Streamwise mean velocity

2 分析与讨论

2.1 多孔介质壁面对湍流统计量和阻力系数的影响

壁湍流流动中产生阻力的方向主要是流向(x方向),流向的雷诺平均方程为

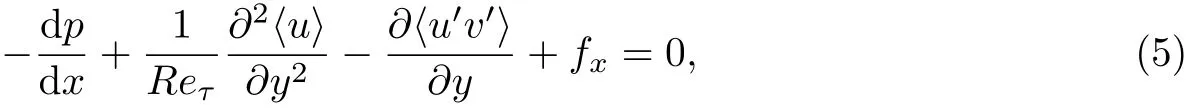
式中,〈u′v′〉为雷诺应力,fx为由流向多孔介质引起的阻力,

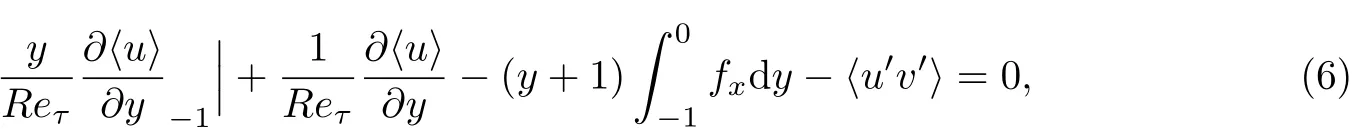
设初始阻力系数最后推导出流体区域流动阻力系数:

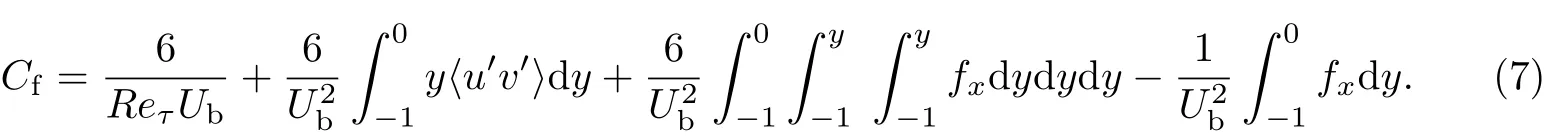
由于多孔介质壁面非常薄,在流场区域内外力项fx=0,本工作认定dy为非线性小量(可以忽略),阻力系数主要来源于层流产生项CL和湍流产生项CT两部分.

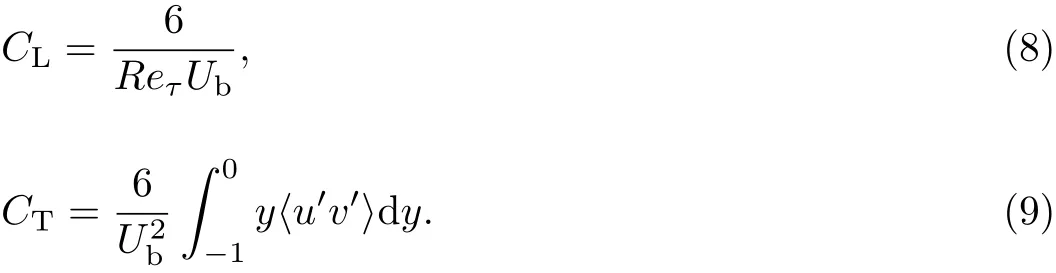
为了验证在分解阻力系数后计算结果的可靠性,本工作将该结果与初始阻力系数公式的计算结果进行比较.

2.1.1 达西数对流场的影响

首先,研究在不同达西数下的阻力系数和湍流脉动量的变化情况(见表1).可以看出,随着达西数的增大,层流产生项CL变化不明显,而湍流产生项CT逐渐减小.这意味着多孔介质层主要通过抑制(增强)湍流脉动强度及雷诺应力来获得减阻(增阻)效果.

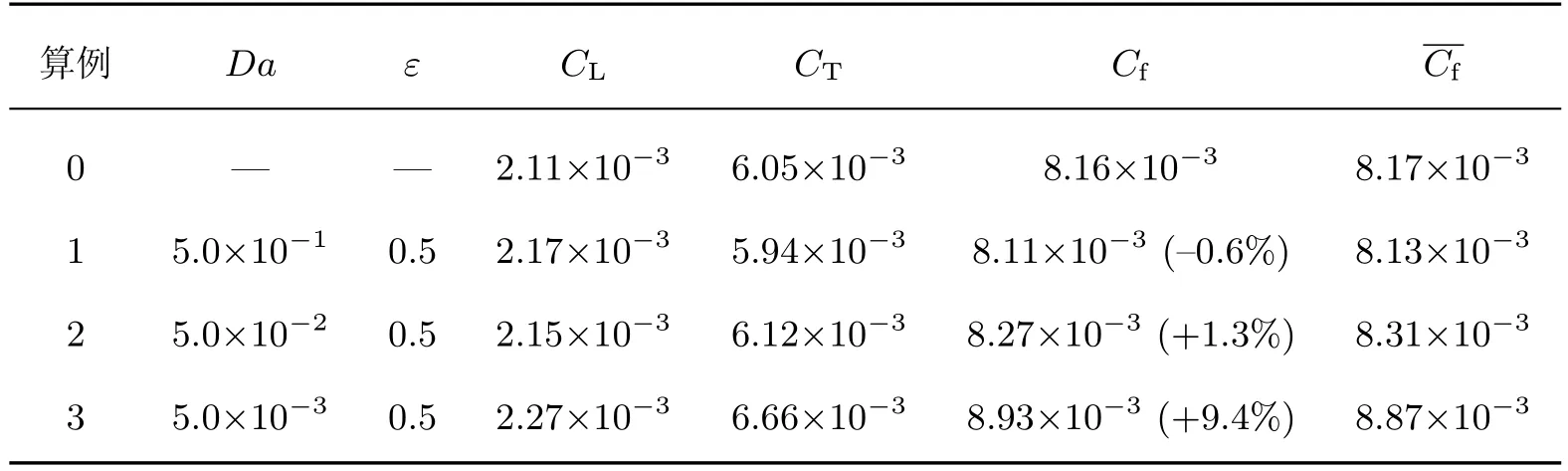
表1 不同达西数下壁湍流阻力系数和湍流脉动量Table 1 Friction coeきcients and turbulence f l uctuation under diあerent Darcy numbers

图3为算例1～3的流向平均速度及3个方向速度脉动均方根分布曲线.随着达西数的减小,近壁区流向平均速度逐渐减小,这是由多孔壁面渗透率减小引起的.然而,在中心区域流向平均速度并非随达西数减小单调递减的.对于流向速度脉动,随着达西数的减小近壁区流向速度脉动减小,峰值向远离壁面方向移动,并且峰值增大中心区域的速度脉动无明显变化;对于法向及展向的速度脉动,随着达西数的减小,整个流场中流向平均速度均有所减小.

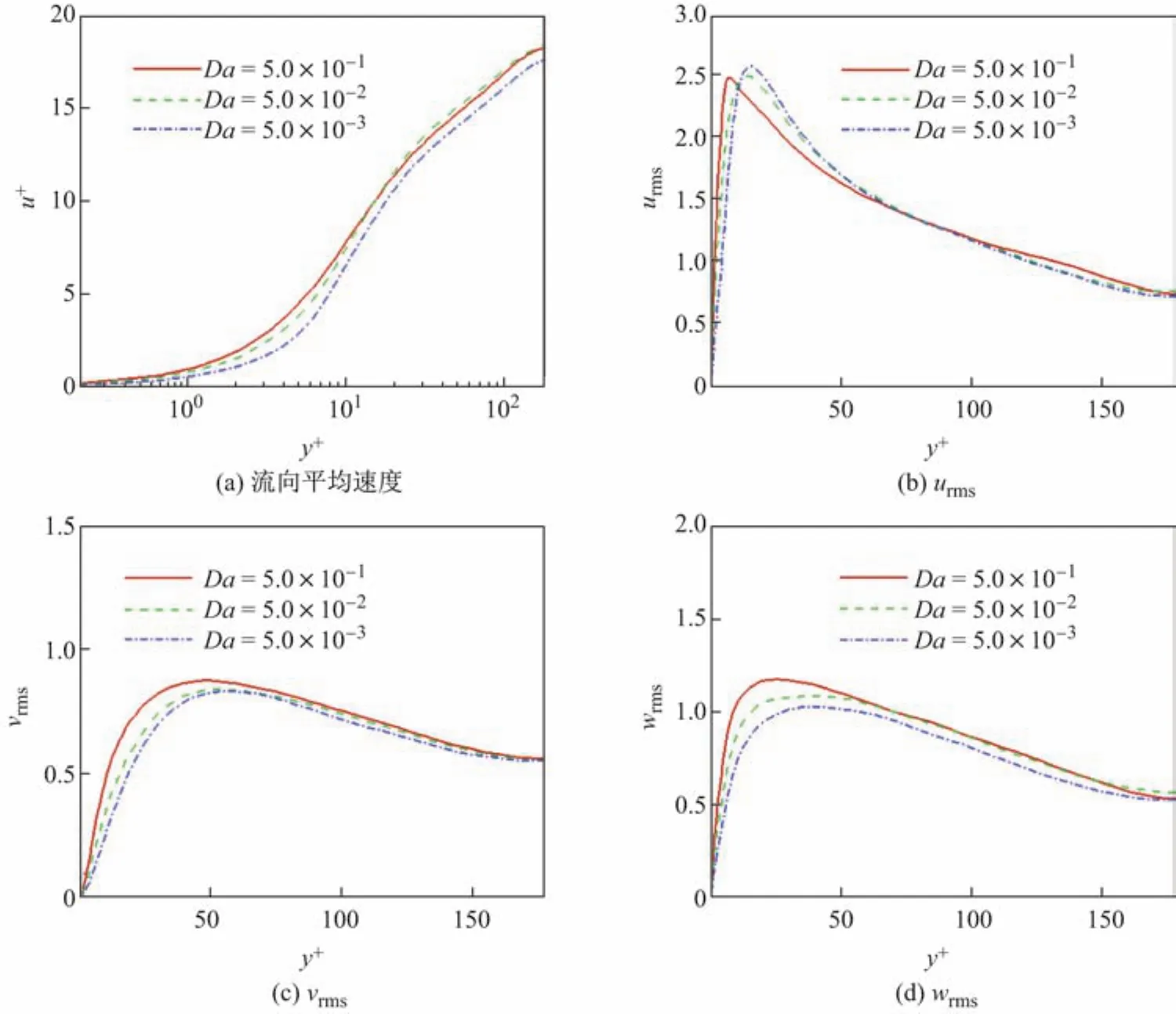
图3 流向平均速度及速度脉动分布Fig.3 Prof i les of streamwise mean velocity and turbulence intensities

2.1.2 孔隙率对流场的影响

为了更进一步探索多孔介质减阻作用,以产生一定减阻效应的算例1为基础,设置了不同孔隙率的算例,以考察孔隙率对流动阻力的影响.当达西数为5.0×10−1时,适当增大孔隙率(ε＞0.5)可以提高减阻效率(见表2).然而,由方程(3)可知,多孔结构内部流体的阻力与孔隙率之间存在复杂的非线性关系,导致阻力系数并非随着孔隙率增大而单调减小.从表中可以看出,当孔隙率大于0.7时,继续增大孔隙率,减阻效率将减小.从图4中可以看出,阻力系数的变化主要受湍流项CT影响,层流项CL变化不明显.

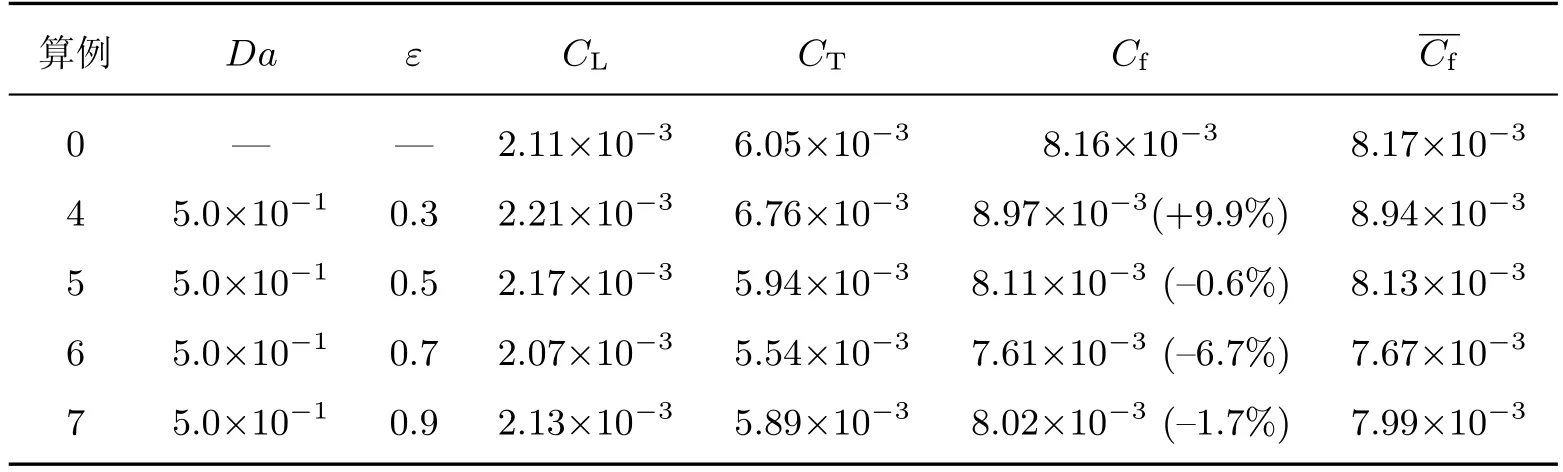
表2 不同孔隙率下壁湍流阻力系数Table 2 Friction coeきcients under diあerent wall-bounded turbulence porosities

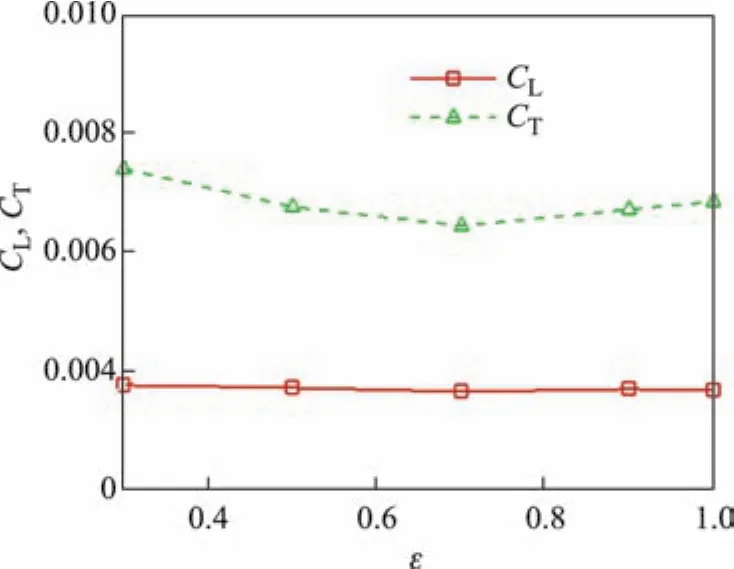
图4阻力系数CL,CT随孔隙率变化Fig.4 Varieties of friction coeきcients CL,CTwith diあerent porosities

图5 给出了当不同达西数时阻力系数随孔隙率变化的曲线图.从图中可以看出,当孔隙率适中(0.5＜ε＜0.7)时,流场阻力减小;而当孔隙率较大(ε＞0.7)或较小(ε＜0.5)时,流场阻力增大.随着达西数的减小,曲线整体上移,阻力系数增大.

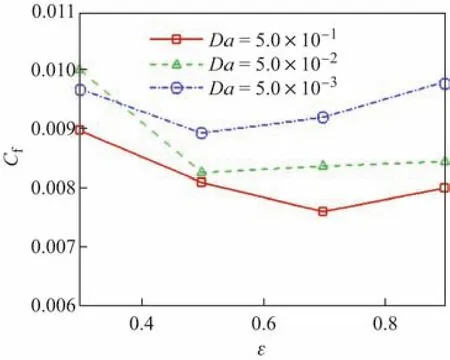
图5阻力系数变化Fig.5 Varieties of friction coeきcients

图6 为不同孔隙率时流向平均速度及速度脉动分布图.从图中可以看出,当孔隙率在0.3～0.7范围内增大时,中心区域流向速度加快,继续增大孔隙率,中心区域流向速度反而下降.图6(b)～(d)中所示的流向速度脉动在近壁区随孔隙率增大而减小,极值点向右移动;而法向和展向速度脉动在整个流场区域均随孔隙率增大而减小.这说明了多孔介质主要通过削弱速度脉动来产生一定的减阻效应.

特别地,选取减阻效应最明显的算例6,给出其与无多孔介质槽道流场在近壁区的流向平均速度对比(见图7).可以发现,在加入多孔介质壁面后,多孔介质壁面附近流向平均速度有所减慢;而在y+＞10的区域,流向平均速度反而加快.这一现象直观地说明了槽道湍流中添加多孔介质壁面提高了湍流输运效率.

图8(a),(b)分别为算例0和算例6的近壁区x-z平面流向瞬时分布图.对比发现,加入多孔介质后低速条纹带数量变多,流向相关性增强,高、低速条带交替变化规律更加明显,这些都是流动减阻的显著特征.

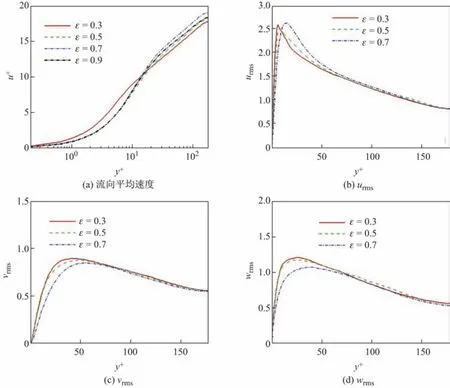
图6 流向平均速度及速度脉动分布Fig.6 Prof i les of streamwise mean velocity and turbulence intensities

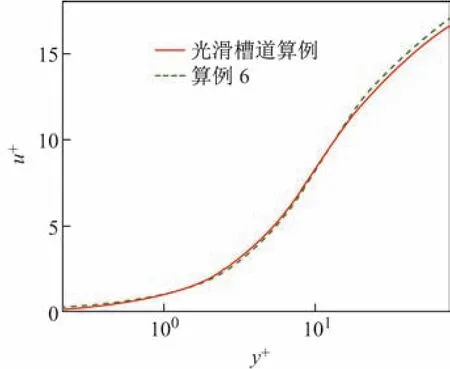
图7 流向平均速度分布Fig.7 Prof i les of streamwise mean velocity

2.2 多孔介质壁面对热场统计量和Nusselt数的影响

2.2.1 上下壁面恒定温度值条件

Nusselt数是湍流传热中表征传热效率的一个重要参量,这里的Nusselt数定义为

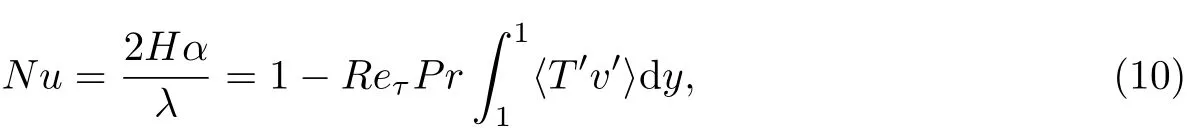
式中,α为热扩散系数,λ为导热系数.为了能更好地对比达西数和孔隙率对热场的影响,本工作定义2组无量纲参数:并结合实际材料(石墨、陶瓷等多孔材料)对其进行赋值(见表3).从表中Nusselt数的变化可以看出,多孔介质壁面既可以增强对流传热强度,也可以削弱对流传热强度,这取决于多孔介质的各项参数.对比算例8～10可以发现,在ε=0.3的情况下,随着达西数的减小Nusselt数减小;对比算例9～13发现,在Da=5.0×10−2的情况下,在一定范围内孔隙率增大Nusselt数减小;当孔隙率大于0.5时,Nusselt数变化不明显.

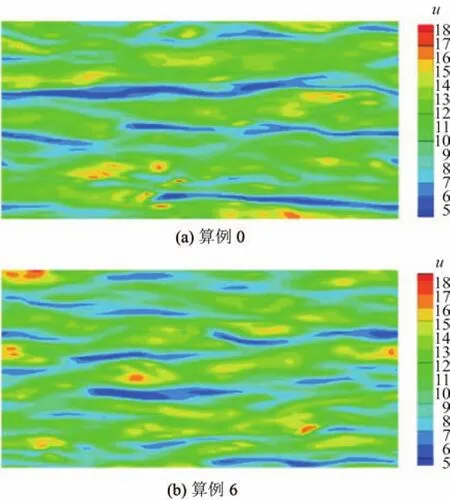
图8 x-z平面流向速度的瞬时分布(y+=15)Fig.8 Instantaneous contours of the velocity f l uctuation in a x-z plane(y+=15)

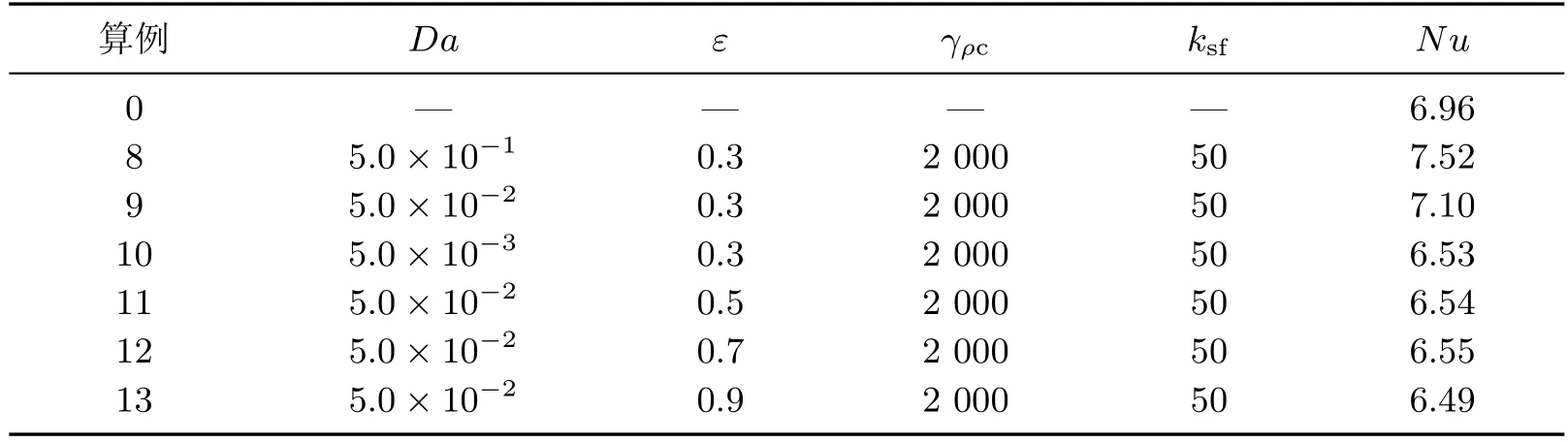
表3 不同参数下壁湍流Nusselt数Table 3 Wall-bounded turbulence Nusselt numbers with diあerent parameters

首先,给出了加入多孔介质壁面前后的平均温度分布曲线(见图9),可以发现在加入多孔介质后中心区域温度变化加快.

图10给出了温度脉动均方根随达西数、孔隙率的分布曲线.在加入多孔介质后近壁区温度脉动均有所减弱,这是因为多孔介质内湍流强度较弱;中心区域温度脉动随达西数的增大而增大,随孔隙率增大而减小.当多孔介质材料孔隙率较大时(ε＞0.5),对温度脉动的影响较小.

图11是平均湍流热通量〈T′u′〉的近壁区图.图中可以看出,在加入多孔介质后,通过改变多孔介质参数,可以增大或减小湍流热通量.在一定范围内有如下规律:随着达西数的增大,平均湍流热通量增大;随着孔隙率增大,平均湍流热通量减小.值得注意的是,和温度脉动变化规律相似,当孔隙率较大时平均湍流热通量无明显变化.

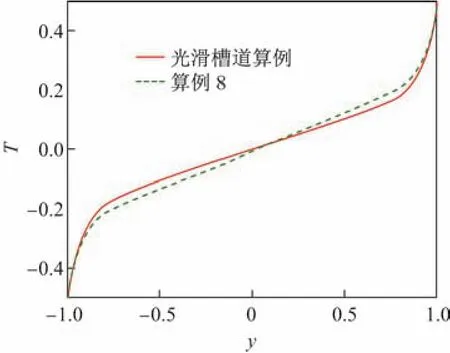
图9 加入多孔介质壁面前后的平均温度Fig.9 Mean temperature before and after the porous wall

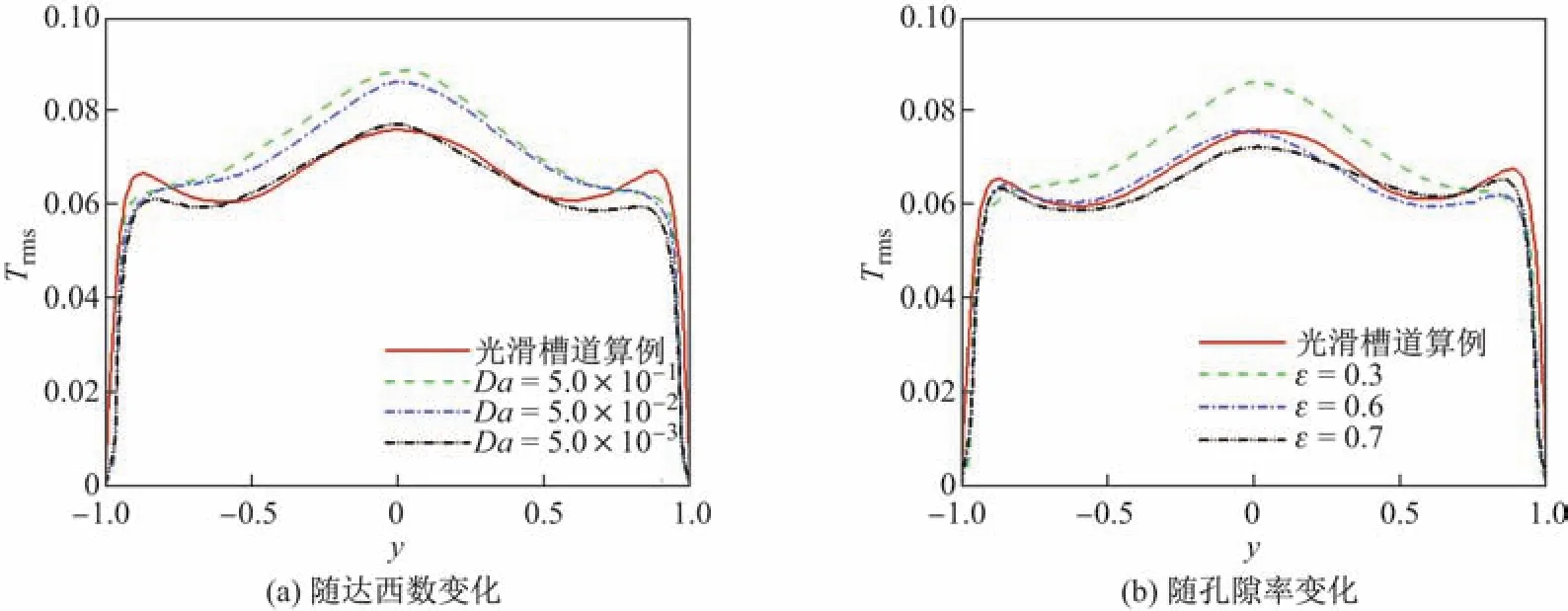
图10 温度脉动均方根分布Fig.10 Prof i les of mean temperature f l uctuation

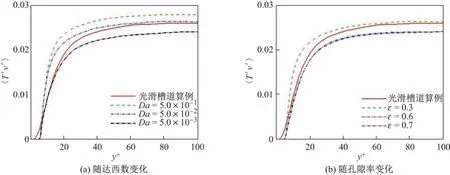
图 11 近壁区平均湍流热通量〈T′u′〉分布Fig.11 Mean turbulent heat f l uxes near the wall

图12(a),(b)给出了算例0和算例8的x-y平面瞬时温度分布.对比可以发现在加入多孔介质后,换热作用更加明显.

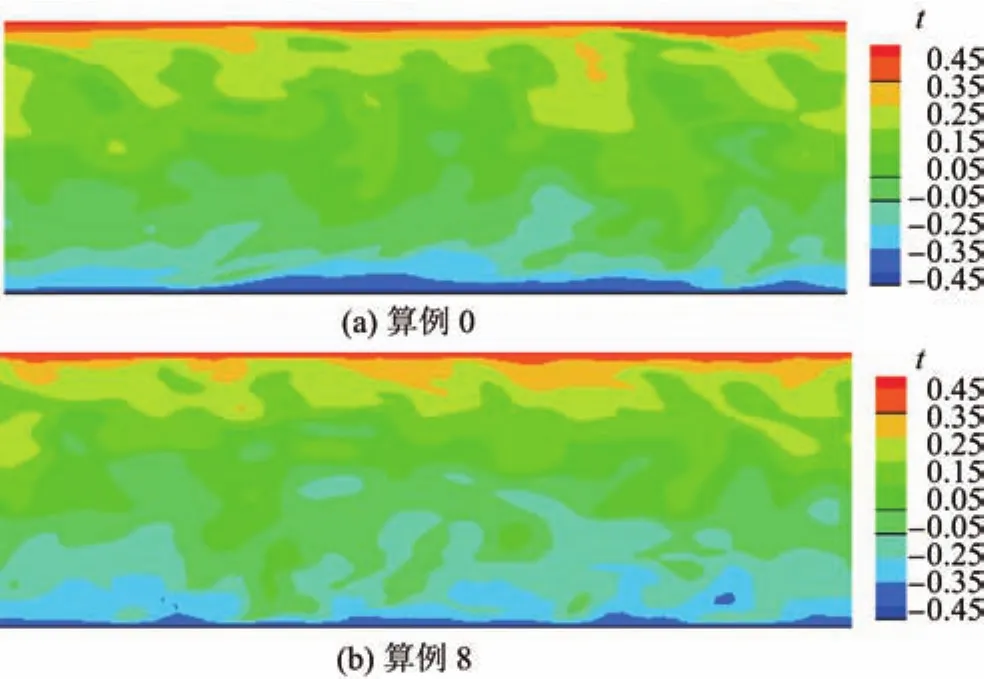
图12 x-y平面瞬时温度分布Fig.12 Instantaneous contours of temperature in x-y plane

表4显示了不同参数下壁湍流Nusselt数.从表4可以看出,虽然设置了不同的孔隙率和达西数,Nusselt数变化仍然符合上述规律.结合速度场可以发现,当流场法向速度脉动降低时,对流传热强度有所减弱;同时,在产生减阻效应时对流传热强度均减弱.

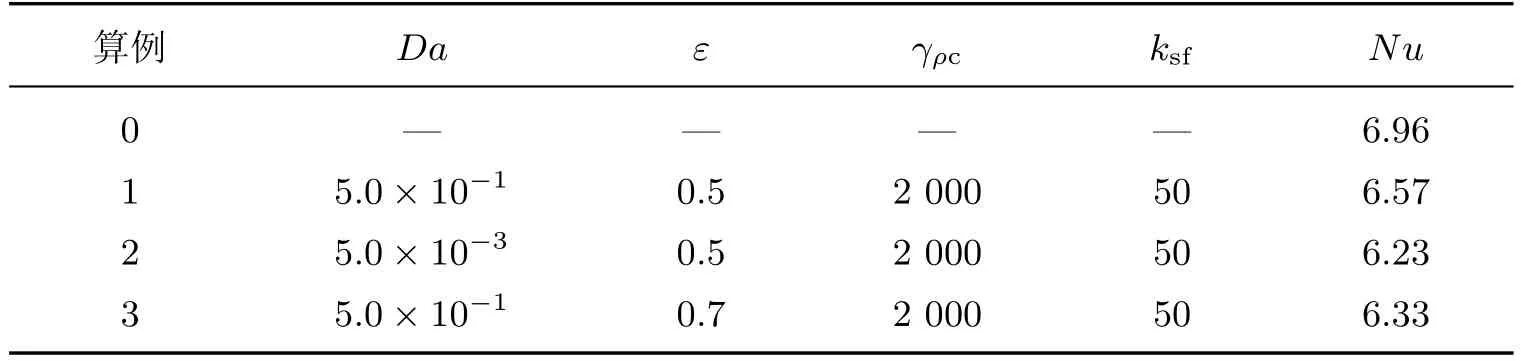
表4 不同参数下壁湍流Nusselt数Table 4 Wall-bounded turbulence Nusselt numbers of diあerent parameters

2.2.2 上下壁面恒定热通量条件

在上下壁面取恒定热通量条件下流场Nusselt数

在这部分研究中,初始时间t=0,由于设置了边界条件和初始条件,随着时间的推进,热量将通过固壁向外界传递,槽道内的平均温度随时间的推移而降低,故通过比较不同参数算例在同一时刻的温度场统计量来比较其传热强度.设置与表3相同参数的算例(见表5),在恒定热通量温度条件下进行模拟计算.从表5中可以看出,与恒定温度值条件类似,设置不同参数的多孔介质壁面,可以增强或减弱传热强度.随达西数的增大,Nusselt数增大;当孔隙率在0.3～0.5范围内增大时,Nusselt数减小;继续增大孔隙率Nusselt数反而增大,这一点与恒定温度值条件有所不同.

表5 不同参数下壁湍流Nusselt数Table 5 Wall-bounded turbulence Nusselt numbers with diあerent parameters

图13(a),(b)分别为平均温度随达西数和孔隙率变化的分布曲线.从(a)中可以看出,随达西数增大平均温度下降,这说明高达西数多孔介质壁面的设置加快了热传递,热量流失更快;与此相反,低达西数可以降低热量的流失速度.这可能是因为随着渗透率的增大,法向速度脉动更剧烈,从而导致热量流失更加剧烈.从图(b)中可以发现,随着孔隙率的增大平均温度升高,当孔隙率较大时这一规律并不明显.

图13不同达西数和孔隙率时平均温度分布Fig.13 Prof i les of mean temperature with diあerent Darcy numbers and porosities

图14 为加入多孔介质壁面前后的温度脉动均方根分布曲线.从图中可以看出,在加入多孔介质后近壁区温度脉动显著减弱,而中心区域温度脉动增强,这一现象与恒定温度值条件类似.

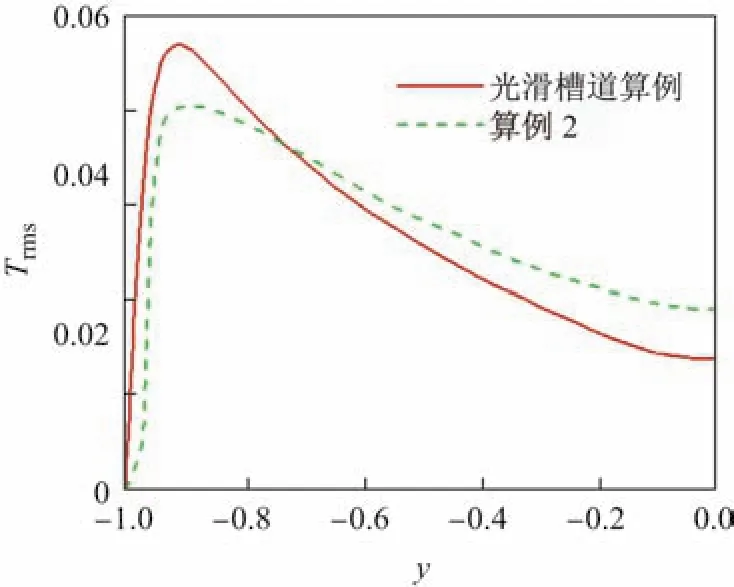
图14 加入多孔介质壁面前后的温度脉动均方根Fig.14 Mean temperature f l uctuation before and after the porous wall

3 结束语

本工作基于体积平均化的概念对含有多孔介质壁面的槽道湍流进行数值模拟,研究了多孔介质壁面对流动和传热的影响.研究发现,加入多孔壁面会影响槽道湍流流动和传热,改变多孔介质参数可以在一定程度上实现减阻,并在一定的参数条件下多孔介质壁面也可以增强对流传热强度.

在本工作范围内,阻力系数随达西数增大而减小;当孔隙率在0.3～0.7范围内增大时,阻力系数减小;继续增大孔隙率,阻力系数增大.另外,阻力系数主要受湍流产生影响,削弱湍流脉动强度可能是导致产生减阻效应的主要原因.在2种不同温度边界条件下,改变多孔介质参数,热场统计信息及Nusselt数变化趋势相似,当达西数增大及孔隙率减小时,对流传热有所增强.同时可以发现,法向速度与传热关系密切,当法向速度脉动较大时对流传热更加剧烈.

在2种温度边界条件下都表现为加入高达西数(渗透率)的多孔介质层,可以有效地增强对流传热强度,这一发现与张红军等[26]研究含多孔介质层的恒温平板在受限层流冲击射流作用下的传热特性时的结论相符合.

综上所述,通过设置高达西数、较大孔隙率(如Da=5.0×10−1,ε=0.7),多孔壁面可以有效增加湍流输运效率,实现流动减阻;设置高达西数、低孔隙率(如Da=5.0×10−1,ε=0.3),多孔壁面会在一定程度上增强对流传热强度,实现传热效率的提高.

[1]BEAR J.Dynamics of f l uids in porous media[M].2nd Ed.New York:Dover Publications Inc,1989.

[2]RICHARDS L A.Capillary conduction of liquids through porous mediums[J].Journal of Applied Physics,1931,1(5):318-333.

[3]FREDLUND D G.Unsaturated soil mechanics in engineering practice[J].Journal of Geotechnical and Geoenvironmental Engineering,2006,132(3):286-321.

[4]MARTYS N S,CHEN H.Simulation of multicomponent f l uids in complex three-dimensional geometries by the lattice Boltzmann method[J].Phys Rev E,1996,53(1):743-750.

[5]JIMENEZ J,UHLMANN M,PINELLI A,et al.Turbulent shear f l ow over active and passive porous surfaces[J].J Fluid Mech,2001,442:89-117.

[6]BRUNEAU C H,MORTAZAVI I.Passive control of the f l ow around a square cylinder using porous media[J].International Journal for Numerical Methods in Fluids,2004,46:415-433.

[7]LU T,JIANG P X,GUO Z J,et al.Large-eddy simulations(LES)of temperature f l uctuations in a mixing tee with/without a porous medium[J].International Journal of Heat and Mass Transfer,2010,53:4458-4466.

[8]MOHAMAD A A.Heat transfer enhancements in heat exchangers f i tted with porous media Part I:constant wall temperature[J].International Journal of Thermal Sciences,2003,42:385-395.

[9]PIVEM A C,DE LEMOS M J S.Turbulence modeling in a parallel f l ow moving porous bed[J].International Communications in Heat and Mass Transfer,2013,48:1-7.

[10]EL SAYED M F,EL DABE N T M,GHALY A Y,et al.Eあects of chemical reaction,heat,and mass transfer on non-newtonian f l uid f l ow through porous medium in a vertical peristaltic tube[J].Transport in Porous Media,2011,89(2):185-212.

[11]KUWAHARA F,SHIROTA M,NAKAYAMA A.A numerical study of interfacial convective heat transfer coeきcient in two-energy equation model for convection in porous media[J].International Journal of Heat and Mass Transfer,2001,44(6):1153-1159.

[12]ALAZMI B,VAFAI K.Analysis of f l uid f l ow and heat transfer interfacial conditions between a porous medium and a f l uid layer[J].International Journal of Heat and Mass Transfer,2001,44:1735-1749.

[13]SAITO M B,DE LEMOS M J S.A macroscopic two-energy equation model for turbulent f l ow and heat transfer in highly porous media[J].International Journal of Heat and Mass Transfer,2010,53:2424-2433.

[14]HAHN S,JE J,CHOI H.Direct numerical simulation of turbulent channel f l ow with permeable walls[J].Journal of Fluid Mechanics,2002,450:259-286.

[15]NIMVARI M E,MAEREFAT M,EL HOSSAINI M K.Numerical simulation of turbulent f l ow and heat transfer in a channel partially f i lled with a porous media[J].International Journal of Thermal Sciences,2012,60:131-141.

[16]SUEKI T,TAKAISHI T,IKEDA M,et al.Application of porous material to reduce aerodynamic sound from bluあbodies[J].Fluid Dynamics Research,2010,42(1):015004.

[17]NAITO H,FUKAGATA K.Numerical simulation of f l ow around a circular cylinder having porous surface[J].Physics of Fluids,2012,24(11):117102.

[18]BREUGEM W,BOERSMA B,UITTENBOGAARD R.The inf l uence of wall permeability on turbulent channel f l ow[J].Journal of Fluid Mechanics,2006,562(1):35-72.

[19]NITHIARASU P,SEETHARAMU K N,SUNDARARAjAN T.Natural convective heat transfer in a fl uid saturated variable porosity medium[J].International Journal of Heat and Mass Transfer,1997,40(16):3955-3967.

[20]TANG Z,LIU N S,DONG Y H.Lattice Boltzmann simulations of turbulent shear f l ow between parallel porous walls[J].Applied Mathematics and Mechanics(English Edition),2014,35(12):1479-1494.

[21]ERGUN S.Fluid f l ow through packed column[J].Chem Eng Prog,1952,48:89-94.

[22]SEKI Y.DNS of turbulent heat transfer in a channel f l ow with diあerent thermal boundary conditions[C]//The 6th ASME-JSME Thermal Engineering Joint Conference.2003.

[23]WANG L,DONG Y H.An investigation of turbulent open channel f l ow with heat transfer by large eddy simulation[J].Computers and Fluids,2005,34:23-47.

[24]KIM J.Turbulence statistics in fully developed channel f l ow at low Reynolds number[J].J Fluid Mech,1987,177:133-166.

[25]ECKELMANN H.The structure of the viscous sublayer and the adjacent wall region in a turbulent channel f l ow[J].J Fluid Mech,1974,65:439-459.

[26]张红军,邹正平.多孔介质中受限层流冲击射流的流动与换热特性[J].化工学报,2012,63(7):2033-2044.本文彩色版可登陆本刊网站查询:http://www.journal.shu.edu.cn