基于模糊C均值改进的粒化特征加权多标签分类算法

柴瑞敏 闫 婷 (辽宁工程技术大学电子与信息工程学院 辽宁 葫芦岛 125105)

0 引 言

传统的监督学习是机器学习研究范畴之一，其中现实世界的每个对象由单个实例表示并与单个标签相关，称作单标签学习。传统监督学习所采用的一个基本假设是，每个例子只属于一个概念，即具有独特的语义意义，然而真实世界的对象可能是复杂的，同时具有多个语义意义[1]。例如，《盗梦空间》这部电影被同时赋予动作、冒险和悬疑三个标签。类似地，在医学诊断中，患者可能同时患有糖尿病和前列腺癌，这些不同于单标签分类，将一个实例同时涉及到多个标签的问题称为多标签学习。近年来，研究者注意到现代智能信息处理越来越多地需要多标签分类方法，如音乐情感分类[2]、文本分类和基因功能组[3]。在音乐情感分类中，歌曲可以属于多种类型，例如，流行摇滚和质朴民谣。在文本分类中，一篇文章可能包含多个领域，如数学和图像分析。

在多标签分类中，每个对象也是由单个实例表示，但它与一组标签而不是单个标签相关，多标签学习的任务就是给定一个未知实例可以正确预测它所属的标签集。从多标签训练集T={(xi,Yi)|1≤i≤m}中学习一个多标签分类器函数h:X→2L。每个多标签实例(xi,Yi)，xi∈X是t维特征向量，Yi∈L是与xi相关的标签集合，其中，F={f1,f2,…,ft}是t维的特征空间，L={l1,l2,…,lq}表示具有q个可能类标签的标签空间，对任意给定的一个未知实例xi∈X，多标签分类器h(·)能够预测h(x)⊆L的正确标签集合。

在学习多标签数据时，随着类标签数量的增加，标签集的数量呈指数增长[1]，使得标签数据复杂多变，增加了标签预测的难度。特征与标签的相关性更为复杂，不同的特征对同一标签的分类有不同的重要度，所以应该根据对标签分类的重要度对不同特征给予相应的权重。

1 相关工作

目前处理多标签分类的方法可归为两类：问题转换法和算法适应法。研究者为了将复杂的问题简单化，利用基于问题转化方法将多标签分类转化为多个单标签分类，如BR(Binary Relevance)二元关系法[1]，该算法的基本思想是将多标签分类问题分解为|q|个二类分类问题，为每一个标签训练一个二分类器，该算法虽然简单、高效，但其忽略了标签间的相关性；ECC(Ensembles of Classifier Chains)集成分类器链[4]，该算法是对BR算法的一种改进，将已训练的样本属性继续代入到下一个分类器中训练，解决了BR算法造成的信息缺失问题，但是随机产生的分类器链组合排序问题会对结果造成不利影响。

LP(Label Powerset)标签密集法[1]，该算法将训练集中样本所属的标签集进行二进制编码，组成新的单标签数据，从而将多标签分类转化成新的多类分类，该算法虽然考虑到了标签间的相关性，但是由于分类器的偏置性使得新的标签组合难以预测且算法复杂度较高；EPS(Ensembles of Pruned Sets)修剪组合算法[5]，该算法根据LP模型中未分类的预测样本用概率分布模型计算标签组合频次，频次较低的将被删除，这样使得算法复杂度降低而且也保证了标签之间的相关性。

算法适应法的思想是改进已经成熟的单标签学习算法，使之去适应多标签数据，如神经网络[6]，该算法考虑了相关标签排序应比不相关标签排序靠前，因此提出了一种排序的误差度量函数。Clare等[7]改进了C4.5用于单标签分类的经典决策树算法，允许叶节点为一个标签的集合，扩展了信息熵的计算公式。Elisseeff等[8]对支持向量机算法改进后提出一种RankSVM算法，其将SVM标签预测模型应用到每个标签上，而后利用排序损失来衡量每个样本的相关标签和不相关标签。

Zhang等[9]提出了ML-kNN，一种多标签懒惰学习算法，先计算测试样本与训练样本间的欧氏距离，从中选取最近的k个近邻样本作为预测标签，通过最大后验概率判断每一个标签的取值，该算法优点是简单、高效，缺点没有考虑多个标签之间的相关性。李峰等[10]提出基于互信息的粒化特征加权多标签学习k近邻算法(GFWML-kNN)，该算法把标签空间粒化，将特征与标签间的相关性融合进特征的权重系数中，考虑了特征和标签之间的关系，但其采用硬划分对标签空间粒化，不能有效表达标签在形态和类属方面的中介性，导致所得的结果偏差较大，而且对于最佳粒化数目没有合理分析。本文提出了基于模糊C均值(FCM)改进的粒化特征加权多标签分类，FCM算法先计算每个样本对所有类的隶属度，得到样本属于各个类的不确定性程度，这种具有样本分类结果可靠性的计算方法，使得聚类结果更加准确灵活。对标签空间进行粒化，用平均信息熵确定最佳粒化数目，平均信息熵能有效衡量某标签的归属程度，其值越小，结果越确定，而后利用信息增益方法对特征进行加权，这样既考虑了标签与特征的相关性，又有效地减少了标签的组合，降低算法复杂度。

2 基础知识

2.1 模糊C划分

本文将模糊C均值(FCM)[11-12]聚类算法应用到标签空间的粒化中，使用隶属度U表示一个标签属于某一标签粒的程度。标签空间L={l1,l2,…,lq}的模糊C划分目标函数为：

(1)

J(U,c1,…,cc,λ1,…,λq)=

(2)

式中:λj=(j=1,…,q)是q个约束式的拉格朗日乘子。对所有输入参量求导，得到隶属度和粒中心的更新公式分别为：

(3)

(4)

2.2 信息增益

定义1信息增益[13]是一种量化随机变量X和Y的关联程度的度量。其值计算如下：

(5)

式中：p(x)表示x的概率密度;p(x,y)是x和y的联合概率密度。

信息增益可由熵和联合熵表示：

IG(X;Y)=H(X)+H(Y)-H(X,Y)

(6)

信息增益能有效描述两个变量之间的关联程度，信息增益越大，关联性越高。

2.3 改进的标签空间粒化及特征加权

本文采用聚类分析中的FCM聚类算法来对标签空间粒化[14]。在问题求解中使用的粒子用Mc表示，标签粒化的过程就是将一系列相似标签划分为一粒，使得相似度大的被划分到同一粒中，不同粒中相似度最小，其中每一个粒是基于相似性或者泛函性聚集得到的一个标签的集合。

在面对具体的复杂问题时，粒化的程度直接影响计算复杂度和效率。既要避免粒度过粗而造成达不到原预计的粒化效果，也要避免粒度过细造成信息的冗余而导致求解效率低下。因此，本文在粒化过程中对于标签粒个数c用平均信息熵来确定。

定义2平均信息熵用来衡量标签空间中的某一标签归属于某一标签粒的程度，该值越小表明归属结果越确定，平均信息熵值可表示为：

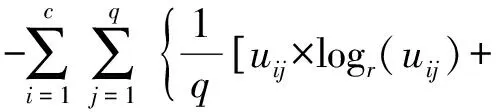
(1-uij)×logr(1-uij)]}

(7)

首先要确定粒化数目的范围，即标签粒的个数，给出最大值和最小值，即k∈[kmin,kmax]，在计算H(k)的过程中使k从kmin增加到kmax，记录下每次变换k所得的平均信息熵值，从中选取使得H(k)最小的粒化数目k作为最终的最佳粒化数c。表1为对emotions[15]数据集的标签空间粒化数目平均熵值表。

表1 emotions的标签空间粒化数目平均熵值表

如表1所示，当粒化数目为2时，平均信息熵取得最小值，因此，在对emotions数据集标签空间粒化时，粒化数目取值为2。

在粒化过程中，FCM算法会根据隶属度的大小分配标签所属的某一标签粒，但这个过程中会出现标签不平衡现象，因此可以采用平衡模糊C均值聚类算法[16]将标签均匀地分配到每个标签粒中，减少标签组合数量，标签粒化过程的步骤如下：

算法1标签粒化过程.

输入：标签空间L={l1,l2,…,lq}，标签粒个数c，训练集T={(xi,Yi)|1≤i≤m}，模糊指数m=2，迭代次数iter;

输出：c个标签粒;

1) 初始化每个标签粒Mi和粒中心ci;

2) Whileiter>0

3) Forlj∈L

4) 计算lj到各个粒中心的欧氏距离dij，将循环变量flag设为真；

5) 根据式(3)计算标签的隶属度值；

6) Whileflag

7) 将lj到各个标签粒的隶属度进行排序，then将lj插入到隶属度最大的中心粒Mi，对标签粒Mi中的标签根据隶属度值的大小进行排序;

8) If |Mi|>「|L|/c⎤ then

9) 将Mi中排在最后的一个标签lk从该标签粒中去除，then把lk插入到其隶属度排名第二的标签粒中，以此类推；

10) Else将循环变量flag设为假；

11) End If

12) End While

13) End FOR

14) 根据式(4)更新各粒中心，迭代次数iter减1;

15) End While

16) 得到标签粒M1,M2,…,Mc.

由算法1得到了C个标签粒，同一特征对不同标签粒的重要性不同，信息增益能有效描述特征与标签粒之间的关联程度，信息增益越大，关联性越高，该特征越重要，相应的权重系数越大，所以标签的分类信息和特征的权重系数是等价的。

(8)

式中：IG(fi;Mc)根据定义1可得：

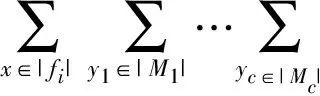
(9)

进而得到加权的欧氏距离，即：

(10)

随后采用经典的kNN算法对未知标签进行预测，该算法是通过计算不同样本之间的距离进行分类，如果一个样本的k个最近邻样本中的大多数属于某一个类别，则该样本也属于这个类别。样本间距离计算常用的就是欧氏距离，本文中加权的欧氏距离包含了特征携带分类信息的多少以及特征与标签之间的相关程度，将特征重要度的差异体现在样本的距离计算中，提高了算法的分类效率及分类结果的准确性。

3 实 验

3.1 数据集

本文采用了来自Mulan[17]平台上的四个公共数据集yeast、medical、genbase、emotions作为实验数据，相关信息如表2所示。

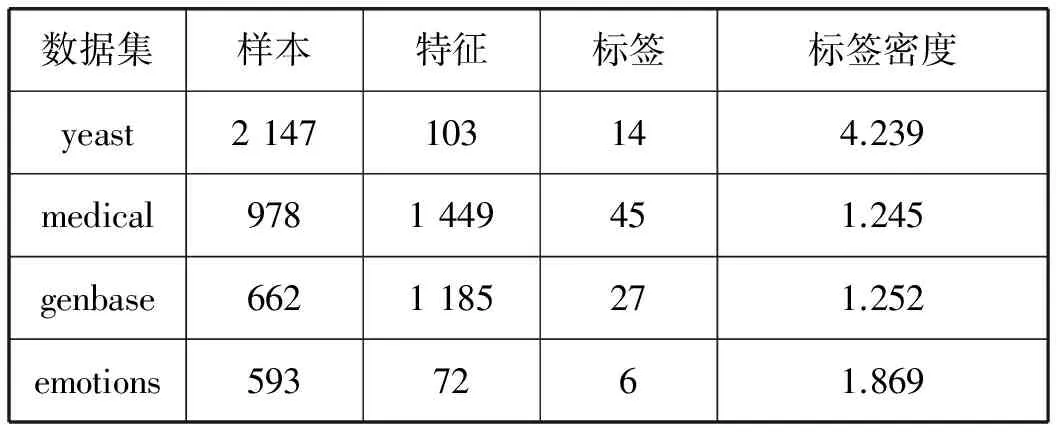
表2 数据集相关信息

3.2 实验结果分析

本文采用多标签分类常用的5大评价指标[9]对实验结果进行分析，5大评价指标分别为HammingLoss、One-Error、Coverage、RankingLoss、AveragePrecision。为了验证所提算法的有效性，本实验将其与经典算法RankSVM[5]、GFWML-kNN[10]、ML-kNN[9]进行了对比，其中近邻数k取值为10、平滑因子取值为1；本实验算法在所给数据集yeast、medical、genbase、emotions的标签粒数目由平均信息熵分别取值为3、8、7、2。如表3-表7所列是各多标签算法在数据集中各项指标的实验结果。其中，表中的粗体字表示各项指标的最优值，(↑)表示取值越大，分类效果越佳；(↓)表示取值越小，分类效果越佳。

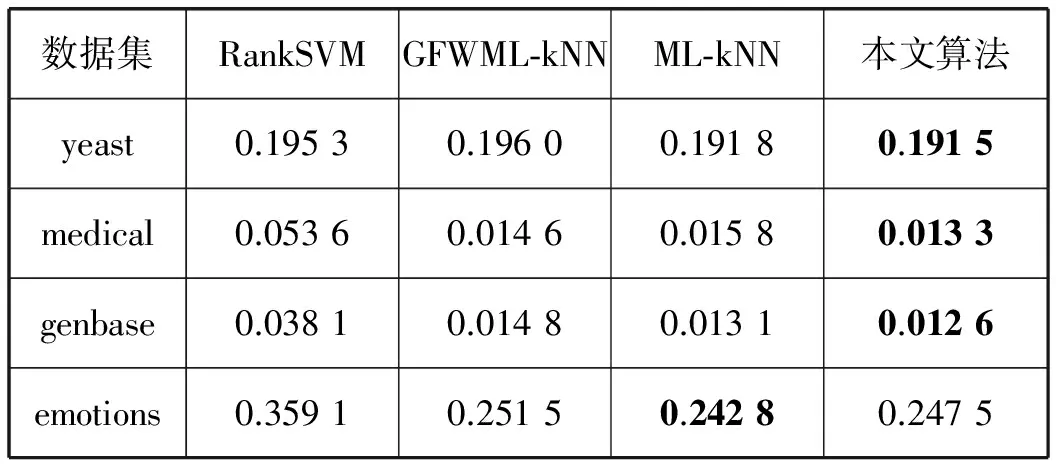
表3 多标签学习算法的HammingLoss(↓)比较

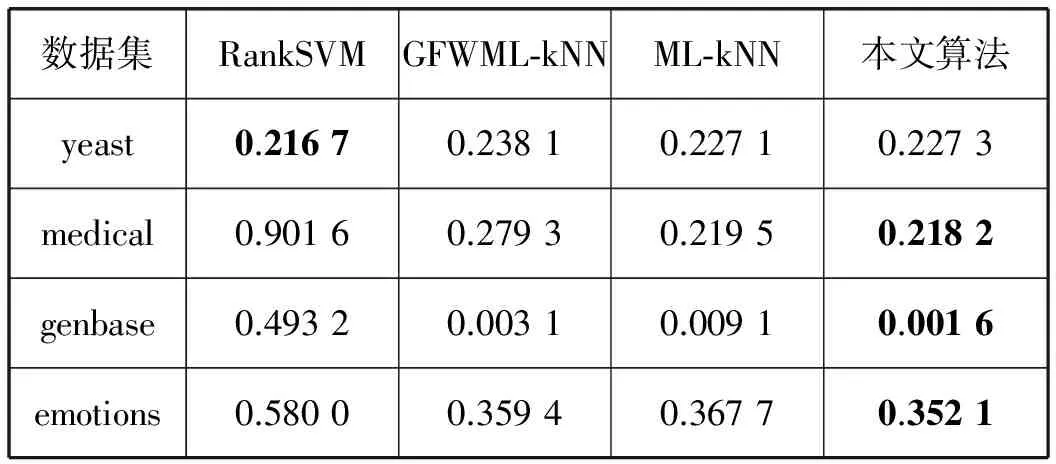
表4 多标签学习算法的OneError(↓)比较

从表3可以看出本文算法在3个多标签数据集上都优于RankSVM和GFWML-kNN；而在数据集emotions中，ML-kNN算法优于其他三个算法取得最优。表4中的数据显示本文算法在多个多标签数据集上效果明显优于其他算法，在yeast数据集上，RankSVM算法算法略优于本文算法。

表5 多标签学习算法的Coverage(↓)比较

表6 多标签学习算法的RankingLoss(↓)比较

表7 多标签学习算法的AveragePrecision(↑)比较

从表5-表7中可以看出，表5中除RankSVM算法外的其他三个算法都在对应数据集中取到过最优值，本文算法分别在数据集medical和emotions上效果明显优于其他算法。表6中除了在数据集yeast中本文算法略低于ML-kNN算法，在其他数据集上本文算法在该项指标中都优于另外三个算法。表7中本文算法和GFWML-kNN算法的效果相当，在不同数据集上都取到过两次最优，其中在yeast数据集上本文算法略高于ML-kNN算法，取得最佳效果。

图1-图3中分别是未粒化的特征加权的ML-kNN[9]算法(①)、本文算法(②)和GFWML-kNN[10]算法(③)随着近邻数k的选择对标签相关性造成的损失，以emotions数据集为例，图中显示了多标签的5项评价指标随着k值增加的变化曲线。

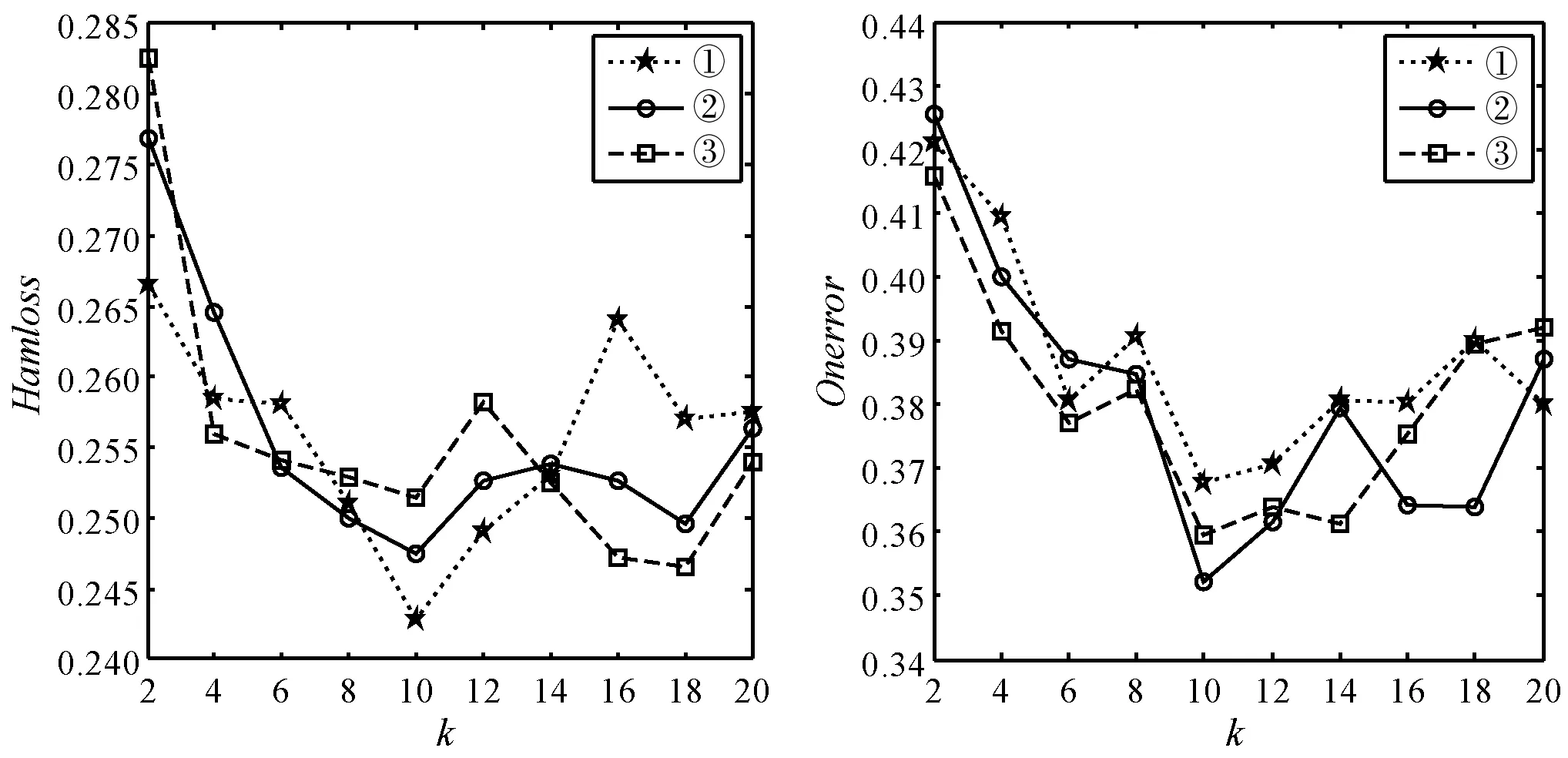
(a) (b)图1 汉明损失和1-错误率随着近邻数k的变化曲线

(a) (b)图2 覆盖率和排序损失随着近邻数k的变化曲线

图3 平均准确率随着近邻数k的变化曲线

从以上三个图中可以看到三个算法随着近邻数k的增加各项损失变化整体趋势很接近，k从2增加到20过程中性能先快速提升，当k=10时达到最优，随后逐渐略微下降。在汉明损失中未粒化的特征加权的ML-kNN算法损失略小于本文算法和GFWML-kNN算法，但在1-错误率、覆盖率、排序损失上，本文算法的性能优于未粒化的特征加权的ML-kNN算法和GFWML-kNN算法，取得最佳；在平均准确率上GFWML-kNN算法略高于本文算法，取得最优值。

4 结 语

针对多标签组合呈指数增长以及特征和标签之间的关系影响分类结果的问题，本文提出了将标签空间利用FCM算法基于平均信息熵进行粒化，形成的标签粒大大减少了标签的组合。而后用信息增益计算特征和标签粒的相关程度，对特征进行加权，使得不同特征携带的分类信息被赋予不同的重要度。在多个数据集上的实验表明该方法在多标签分类问题中取得较好的效果。下一步研究工作将在继续优化该算法使之能处理含有大量标签的数据集上进行开展。

[1] Zhang M L, Zhou Z H. A Review on Multi-Label Learning Algorithms[J]. IEEE Transactions on Knowledge & Data Engineering, 2014, 26(8):1819- 1837.

[2] Sanden C,Zhang J Z. Enhancing multi-label music genre techniques[C]// Proceedings of the 34th International ACM SIGIR Conference on Research and Development in information Retrieval(SIGIR’11). New York, USA, 2011: 705- 714.

[3] Wu J S, Huang S J, Zhou Z H. Genome-Wide Protein Function Prediction through Multi-instance Multi-label Learning[J]. IEEE/ACM Transactions on Computational Biology & Bioinformatics, 2014, 11(5):891- 902.

[4] Read J, Pfahringer B, Holmes G, et al. Classifier chains for multi-label classification[J]. Machine Learning, 2011, 85(3):333- 359.

[5] Read J, Pfahringer B, Holmes G. Multi-label Classification Using Ensembles of Pruned Sets[C]// Eighth IEEE International Conference on Data Mining. IEEE, 2009:995- 1000.

[6] Chen G, Ye D, Xing Z, et al. Ensemble application of convolutional and recurrent neural networks for multi-label text categorization[C]// International Joint Conference on Neural Networks. IEEE, 2017:2377- 2383.

[7] Clare A,King R. Knowledge discovery in multi-label phenotype data[C]//Proceedings of 5th European Conference on Principles of Data Mining and Knowledge Discovery (PKDD). Freiburg,Germany, 2001: 42- 53.

[8] Elisseeff A, Weston J. A kernel method for multi-labelled classification[C]// International Conference on Neural Information Processing Systems: Natural and Synthetic. MIT Press, 2001:681- 687.

[9] Zhang M L,Zhou Z H. ML-kNN: A lazy learning approach to multi-label learning[J]. Pattern Recognition, 2007(40): 2038- 2048.

[10] 李峰,苗夺谦,张志飞,等.基于互信息的粒化特征加权多标签学习k近邻算法[J].计算机研究与发展,2017,54(5): 1024- 1035.

[11] 文传军,汪庆淼,詹永照.均衡模糊C均值聚类算法[J].计算机科学,2014,41(8): 250- 253.

[12] 廖松有,张继福,刘爱琴.利用模糊熵约束的模糊C均值聚类算法[J].小型微型计算机系统,2014,35(2): 379- 383.

[13] Cover T M,Thomas J A. Elements of information theory [M]. John Wiley & Sons, 2012.

[14] 徐计,王国胤,于洪.基于粒计算的大数据处理[J].计算机学报,2015,38(8): 1497- 1517.

[15] Trohidis K,Tsoumakas G,Kalliris G,et al. Multi-label classification of music into emotions[J]. Eurasip Journal on Audio Speech & Music Processing, 2008, 2011(1): 325- 330.

[16] Shannon C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(4):379- 423.

[17] Tsoumakas G, Spyromitros-Xioufis E, Vilcek J, et al. MULAN: A Java library for multi-label learning[J]. Journal of Machine Learning Research, 2012, 12(7):2411- 2414.