基于托轮振动的回转窑故障诊断研究

胡昭中，张 云

(1.武汉理工大学 机电工程学院，湖北 武汉 430070;2.武汉理工大学 建材行业回转窑检测技术中心，湖北 武汉 430070)

回转窑是水泥行业的核心生产设备，它主要由筒体、托轮机和轮带构成。由于回转窑长期处于重载、高温且温度经常变化的工况中，在筒体表面温度分布不均以及内部物料出现“雪球效应”的影响下，筒托会产生弯曲等变形。研究表明：回转窑能否正常运行取决于托轮的运行状况[1]，表1为丹麦Smith公司2009年在丹麦哥本哈根举办的国际设备维护研讨会上提出的回转窑故障模式及危害性分析[2]。由表1可看出，综合考虑故障严重程度和危险系数，筒体热弯曲和窑中心线偏差在回转窑设备各种故障中最为危险。它们会造成托轮过载、托轮接触表面疲劳破坏等问题。如果短时间内筒体突发和持续过度热膨胀可能导致托轮滑动轴承升温，甚至引起“烧瓦”停窑等严重事故。

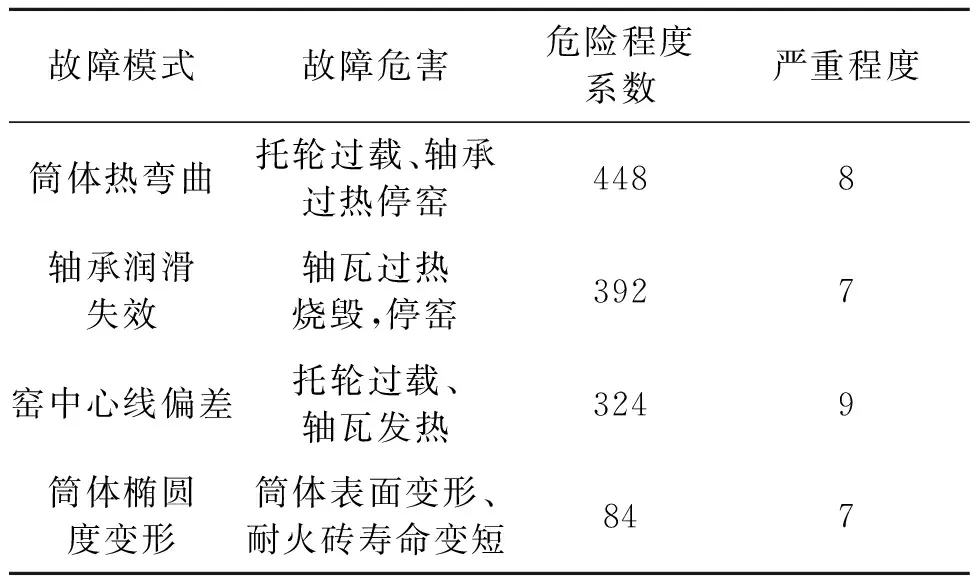
表1 回转窑主要故障模式

筒体弯曲和回转窑中心线偏差产生动态载荷会通过轮带传递到托轮上，即它们可以由托轮的径向位移振动来表征。通过对托轮振动信号分析来提取循环冲击载荷以及托轮挠度变化等特征信息，可判断筒体弯曲特别是热弯曲和托轮承载受力状况。由于受托轮表面凹状变形、表面疲劳裂纹、掉块等因素影响，托轮振动信号在多数情况下呈现非线性非平稳性特征[3]，其中的故障特征信息较微弱，极易被噪音所淹没。因此，选择恰当的信号处理方法从托轮振动信号中降低噪音，准确提取故障特征信息，是判断回转窑运行状态的关键，这对早期诊断筒体弯曲故障原因，保障回转窑正常生产有重要意义。

在回转窑设备的故障诊断研究中，国外Eugeniusz Rusinski等将托轮信号看做平稳信号，采用快速傅里叶变换(fast fourier transformation,FFT)对托轮位移信号处理，发现其主要包括筒体谐波和托轮谐波两个成分，但是实际托轮信号常表现非平稳特性，FFT处理非平稳信号只能得到特征时间历程的平均化，不能得到详细的故障特征信息。国内张云等运用经验模态分解(empirical made decompasition,EMD)方法来直接处理筒体外轮廓信号，分析筒体故障类型[4]。这种故障诊断方法直接从筒体着手，但是对于支撑处的筒体难以直接测量，因此也不能解决全部问题。针对这些问题，笔者提出基于托轮振动的回转窑故障诊断方法。

1 动力学模型建立与仿真分析

1.1 筒体、托轮振动模型建立

在回转窑运转过程中，因为筒体热弯曲变形，在筒体各轮带和托轮处的负载会产生周期性的变化。在建立模型过程中，把筒体及其内部的物料作为一个整体考虑。因为物料的翻滚受本身的质量影响，筒体整体的质心与回转中心不重合，因此将回转窑体内物料等效为质量不均匀的转子模型，如图1(a)所示。筒体转速很低，约3～4 r/min，可视为刚性转子。为方便建模，在轮带与托轮接触的筒体截面处建立如图1所示的坐标系。同理，托轮的转动也视为刚性转子系统，如图1(b)所示。

图1 筒体、托轮振动模型

根据质心运动定理可知，筒体沿着x轴和z轴振动微分方程如式(1)所示。

(1)

同理，建立托轮振动微分方程如下：

(2)

式中：m1为支撑处筒体轮带等效质量；m为托轮等效质量；k1为轮带托轮等效接触刚度；k为托轮轴瓦等效接触刚度；c1为轮带托轮等效接触阻尼；c为托轮轴瓦等效接触阻尼；e为筒体质心与几何中心的偏心距；δ为托轮旋转挠度变化不平衡量；ω1为筒体旋转角速度；ω为托轮旋转角速度；β为筒体托轮中心线方向与竖直方向的夹角；x1和x分别为筒体及托轮沿着x方向的振动位移；z1和z分别为筒体及托轮沿着z方向的振动位移。

1.2 仿真参数设定

建立筒体和托轮的动力学方程后，使用4阶Runge-Kutta数值方法求解式(1)、式(2)，在迭代过程收敛后，可得托轮振动信号的位移变化规律。以实测回转窑为例，窑3档支撑，长度为74 m, 筒体直径为5 m，煅烧产量为5 000 t/d。托轮的基本材料为各向同性的ZG42GrMo，密度为7.8×10-6kg/mm3，半径为1 100 mm。轮带材料为ZG55。根据以上数据，托轮的参数估计值如表2所示。

表2 仿真参数表

1.3 仿真分析及结果

基于所建立的托轮振动模型，对以下两种故障情况下托轮信号进行仿真处理和分析。筒体的偏心距e反映筒体热弯曲变形的程度；托轮不平衡量δ反映托轮径向受力状况，即托轮位置相对窑中心线偏差的程度。当保持筒体偏心距e不变，改变托轮不平衡量δ的大小，仿真分析的时域、频域图如图2(a)和图2(b)所示。某托轮位置相对窑中心线偏差较大时，同档两个托轮中会有一个托轮径向受力较大，即该托轮不平衡量δ就较大。当托轮不平衡量δ不变，改变筒体偏心距e的大小，仿真分析的时域、频域图如图2(b)和图2(c)所示。

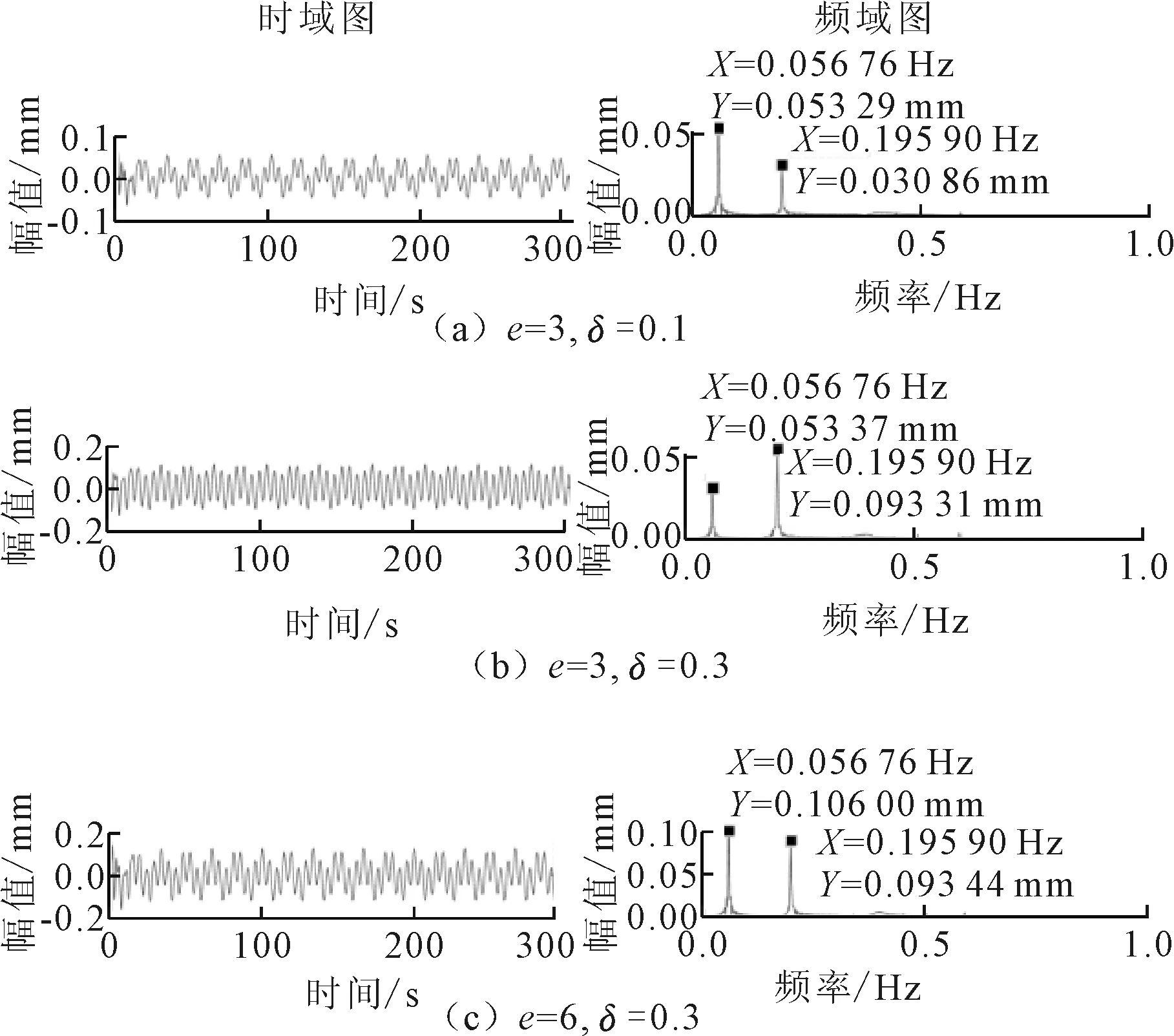
图2 仿真图形

仿真分析建立的动力学模型中，筒体的转速设为0.367 9 rad/s，筒体的特征频率Fs为0.058 55 Hz，与频谱中的0.056 76 Hz吻合，托轮的转速为1.288 rad/s，托轮的特征频率Fr为0.204 9 Hz，与频谱中的0.195 9 Hz吻合。由仿真结果可知，当托轮不平衡量δ不变，筒体偏心距e增大时，筒体特征信号Fs所对应的幅值明显增大，而托轮特征信号Fr所对应的幅值基本不变；当筒体偏心e不变时，托轮不平衡增大时，托轮特征信号Fr所对应的幅值明显增大，而筒体特征信号Fs所对应的幅值基本不变。这说明筒体热弯曲变形故障加深时，托轮信号中Fs所对应的幅值会增大，Fr所对应的幅值基本不变；线偏移加深时，受力增大的托轮其信号中Fr所对应的幅值会增大，Fs所对应的幅值基本不变。

2 托轮信号的时频分析

为验证上述仿真结果的正确性，笔者对四川省某5 000 t/d回转窑托轮挠度变化信号进行了数据采集及处理分析。所测窑筒体转动周期为16 s左右，筒体直径为5 000 mm，1、3档托轮直径为1 800 mm，2档托轮直径为2 100 mm。所用仪器主要包括：数据采集卡、电涡流传感器、霍尔开关、笔记本电脑。数据采集频率为100 Hz。

2.1 小波变换与经验模态分解方法的对比

处理平稳信号最常用的主要方法是傅立叶变换。该方法建立了信号从时域到频域的变换桥梁，但是它只能整体上将信号分解为不同的频率分量，缺乏局域性信息，即对信号的表征或是完全在时域，或是完全在频域，它不能揭示某种频率分量何时出现及随时间变化的情况[5]。托轮的振动位移信号一般是非平稳信号，目前分析非平稳信号使用较广泛的方法包括小波变换和经验模态分解。

小波变换是一种时频分析方法，具有多分辨率分析的特点，在时域和频域都有表征信号局部信息的能力[6]，小波变换对实际托轮信号的分解结果如图3所示。

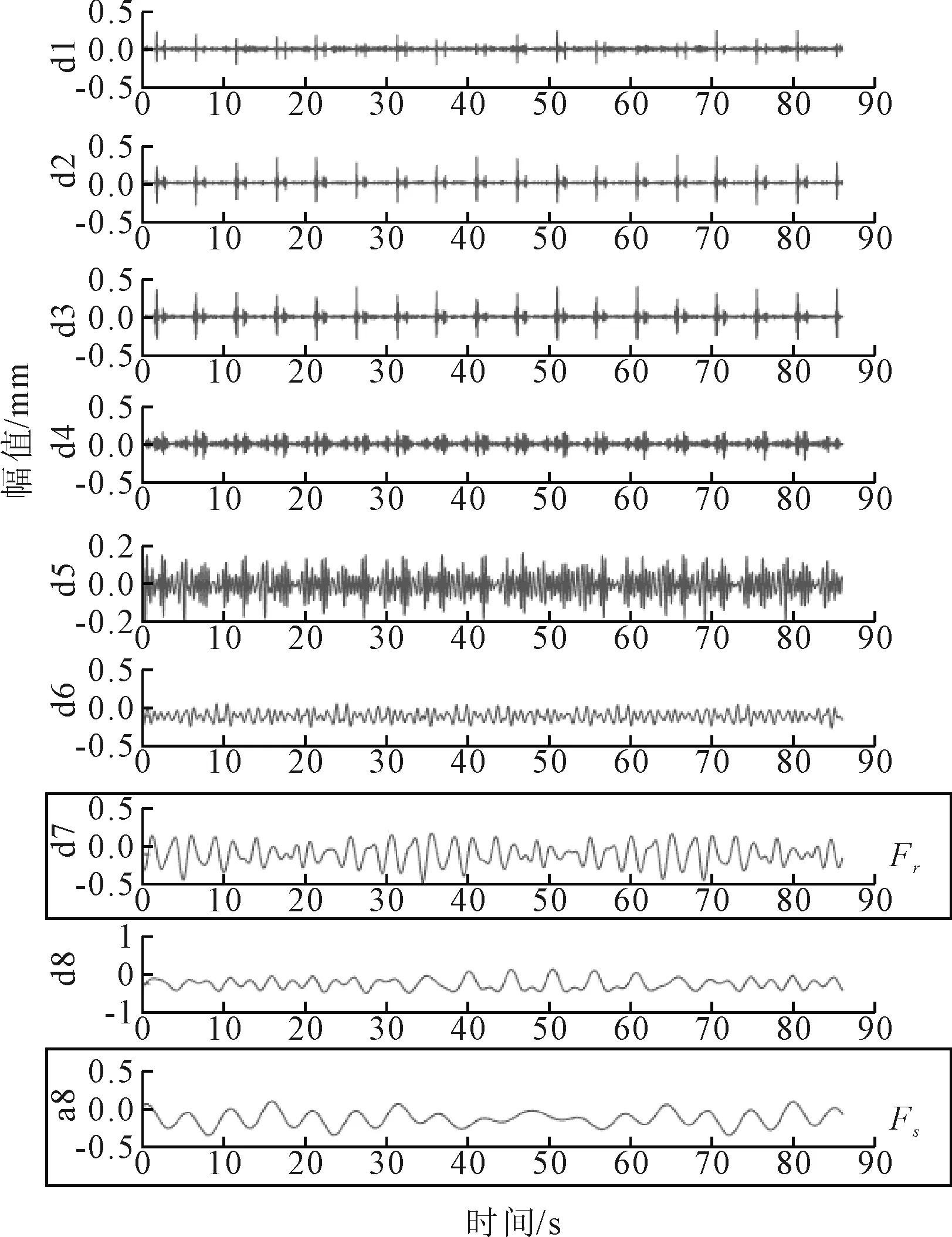
图3 小波变换处理结果

EMD是将信号分解为若干个单分量信号，且每个单分量信号理论上只含有一种振荡模式[7]，EMD对实际托轮信号分解结果如图4所示。

对比图3和图4，EMD得到的IMF6、IMF7相对于小波分析结果中的d7细节信号、a8近似信号更加光滑，表明EMD对托轮信号中的特征振动模式刻画更加清晰、明确。为定量对比小波变换和EMD对托轮信号的处理效果，采取相关系数ρ、均方根误差RMSE和信噪比SNR作为衡量指标。3个衡量指标的计算公式如下：

(3)

(4)

(5)

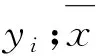
小波变换和EMD得到的相关系数ρ、均方根误差RMSE和信噪比SNR如表3所示。

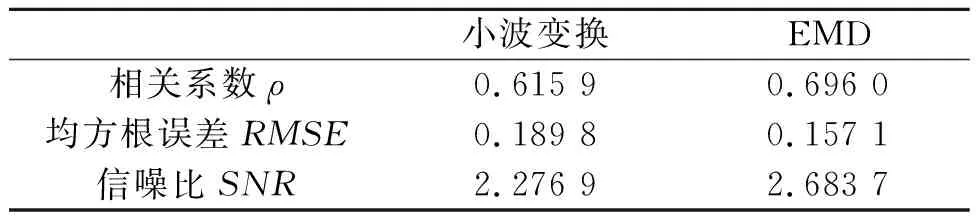
表3 小波变换和EMD的对比结果

由表3可知，EMD处理结果中，特征谐波重构信号的RMSE值相对较小，而SNR值相对较大，表明EMD方法对于托轮信号的故障提取更加精确。而EMD重构信号得到的相关系数ρ更大，说明EMD方法重构的信号与原始信号的相关性更大，表明了EMD提取的谐波成分，更加接近于托轮的实际信号中包含的故障特征信息。

2.2 基于EMD方法的回转窑故障诊断及实验对比验证

EMD方法处理6个托轮信号，所得各托轮信号中Fs所对应的幅值统计如图5所示。在图5中，1档Fs所对应的幅值第二，2档Fs所对应的幅值第一，3档Fs所对应的幅值第三。根据EMD处理结果可以判断2档筒体偏心最大，1档筒体偏心第二，3档筒体偏心最小。

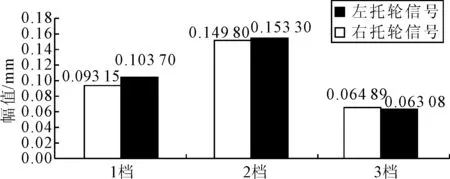
图5 各托轮Fs幅值

文献[8]使用激光测距测量法直接对筒体偏心进行测量，其筒体弯曲变形结果如图6所示。1档筒体偏心最大，3档偏心最小，这与图5的结果一致，符合窑现场实际情况。

EMD方法处理6个托轮信号，所得各托轮信号中Fr所对应的幅值如图7所示。在图7中1档左、右托轮特征频率Fr所对应的幅值比例约4.3倍，即左托轮比右托轮径向受力比例大4.3倍；2档左、右托轮特征频率Fr所对应的幅值基本相同，即两托轮径向受力基本相同；3档的左、右托轮特征频率Fr所对应的幅值比例约0.47倍，即左托轮径向受力小于右托轮0.47倍。

图7 各托轮Fr幅值

文献[9]对该窑使用精度0.001 mm的专利椭圆仪在各轮带旁对筒体椭圆度作在线测量，在测量曲线右边两个相邻的小波谷的幅值比例可以反映左右两托轮径向相对受力的大小,其实际测量曲线如图8所示。1档左托轮波谷幅值约为0.022 mm，右托轮的波谷幅值为0.005 mm，左托轮的幅值是右托轮的4.4倍；2档左右托轮波谷幅值都约为0.011 mm；3档左托轮波谷幅值约为0.009 mm，右托轮的波谷幅值约为0.021 mm，左托轮的幅值是右托轮的0.43倍，这与图7结果基本一致。

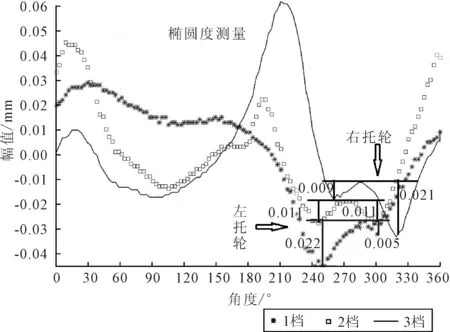
图8 四川省某窑筒体椭圆度测量曲线结果

通过筒体偏心和椭圆度的工程测量数据验证了本处理方法的正确性和有效性。

3 结论

笔者建立了筒体及托轮振动动力学模型，提出了基于托轮振动信号的时域和频域特征的故障诊断方法。通过小波变换与EMD方法对实际数据处理的对比，选择EMD方法进行信号处理。将EMD处理结果与传统测量结果进行对比，结果证明了动力学模型及EMD处理方法的有效性及正确性，为回转窑故障诊断提供了一种新的思路。

参考文献：

[1] 张云,闫东晓.回转窑托轮轴向受力的分析与检测[J].水泥工程,2010(1):51-53.

[2] Rusinski E, Stamboliska Z, Moczko P. Proactive Control System of Condition of Low-speed Cement Machinery[J]. Automation in Construction, 2013,31(3):313-324.

[3] Zheng K, Zhang Y, Zhao C, et al. Rotary Kiln Cylinder Deformation Measurement and Feature Extraction Based on EMD Method[J]. Engineering Letters, 2015,23(4):283-291.

[4] 张云,周达,郑凯.回转窑筒体变形数据的混合编程处理新方法[J].水泥工程,2017(1):21-24.

[5] 葛哲学，陈仲生.MATLAB时频分析技术及其应用[M].北京：人民邮电出版社,2006.

[6] 肖大雪.Matlab小波分析在信号处理中的应用[J].科技广场,2011(1):60-64.

[7] 胡广书.现代信号处理教程[M].北京：清华大学出版社,2015.

[9] 张云,刘圣池.回转窑筒体变形对衬砖影响及其测量曲线的研究[J].水泥工程,2011(3):63-67.