RV减速器的摆线针轮传动齿面接触分析

张月娜

(1.武汉理工大学 汽车工程学院，湖北 武汉 430070；2.武汉理工大学 现代汽车零部件技术湖北省重点实验室，湖北 武汉430070)

由于较大的传动比、较高的回转精度与传动效率等优点，摆线针轮行星传动在多个领域得到了广泛的应用，由其衍生的RV(rotate vector)行星传动也越来越受到人们的重视。摆线针轮行星传动在设计时需要进行强度校核[1-3]，特别是齿面接触强度的校核。采用传统的校核公式计算繁琐，效率低下，而且不能反映实际工况，误差较大。而有限元方法则能够有效简化计算，减小计算误差。

国内外诸多学者采用有限元方法在RV传动接触方面进行了广泛的研究。Manfred等[4]采用有限元法对摆线齿廓的接触力和接触变形进行计算，对载荷分布进行了分析。Bobach等[5]运用有限元法进行了渐开线直齿圆柱齿轮的热弹流摩擦模拟。王文涛[6]利用APDL语言对RV传动进行热—结构耦合分析，对齿面接触应力进行了有限元分析。姚灿江等[7]利用ANSYS仿真摆线轮传动过程，分析其啮合过程的接触应力。

然而，当前的研究主要集中在无误差的摆线针轮传动接触方面，在摆线针轮齿廓误差对其传动接触特性影响的研究方面较为有限，针对齿廓误差因素对摆线针轮副接触的研究基本上处于空白状态。因此，笔者在RV减速器摆线针轮传动的基础上，进行了摆线针轮齿廓误差对齿面接触影响的研究，并得出了一定的规律。

1 摆线针轮副误差模型的建立方法

RV减速器的摆线针轮副的误差因素[8-11]有：针轮(针齿壳)中心圆半径偏差；针齿半径误差；针轮(针齿壳)与针齿的配合间隙；摆线轮齿圈径向跳动；针轮(针齿壳)孔圆周位置度误差；摆线轮齿廓周节误差；摆线轮等距修形误差；摆线轮移距修形误差；针轮单齿距偏差等。误差种类较多，在笔者的研究中，主要考察了摆线轮等距修形误差、移距修形误差、针齿半径误差和针齿中心圆半径误差对摆线针轮副齿面接触的影响。

1.1 摆线轮齿廓曲线方程

摆线轮是RV减速器的核心关键部件，其齿廓形状是影响该类减速器传动性能的关键环节。摆线轮轮齿齿廓曲线一般有两种形成方法，一种为外切外滚法，另一种是内切外滚法。虽然两种形成方法不尽然相同，但是可以通过参数的统一生成一样的摆线轮轮齿外摆线，以此形成相同的摆线轮轮齿齿廓曲线。

根据摆线针轮传动(RV传动)的啮合原理与其展成法切削加工原理，摆线轮的齿形修形方式一般有3种：等距修形、移距修形和转角修形。可以概括3种修形方式的通用摆线轮齿廓曲线方程如下[7]：

(1)

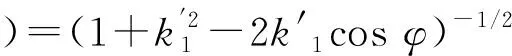
1.2 三维几何模型的建立

使用三维软件Pro/E中的程序设计功能，设计好摆线轮基本参数与各参数之间的关系，通过提前编辑的方程生成摆线轮轮齿齿廓曲线，实现摆线轮轮齿齿廓曲线的参数化建模。摆线轮与针齿的基本参数如表1所示。

表1 摆线轮与针齿的基本参数

生成摆线轮齿廓曲线后，再在齿宽方向拉伸得到完整的摆线轮三维模型，如图1所示。通过修改摆线轮齿廓的相关参数，可以建立不同的摆线轮模型。针轮模型也可以用同样的方法建立。摆线轮与针轮装配后得到的摆线针轮副三维模型，如图2所示。由于本文主要研究的是摆线齿与针齿的齿面接触分析，模型删除了摆线轮中心部分的结构，方便后续有限元计算，减少计算时间。

图1 摆线轮三维模型

图2 摆线针轮副三维模型

RV减速器摆线针轮副的误差因素很多，笔者主要研究了摆线轮等距修形误差、移距修形误差、针齿半径误差和针齿中心圆半径误差对摆线针轮副齿面接触的影响。

先建立7组模型(第一组模型0是标准无误差的)来研究摆线轮两种修形误差对齿面接触的影响，1、2组模型采用“负移距+零等距”修形误差参数组合，3、4组模型采用“零移距+正等距”修形误差参数组合，5、6组模型采用“正移距+正等距”修形误差参数组合，具体误差参数如表2所示。

为了研究针齿销相关的误差对齿面接触的影响，建立6组模型，7、8组模型研究针齿半径误差的影响，9、10组模型研究针齿中心径向误差的影响，11、12组模型研究“负针齿半径误差+针齿中心径向误差”的影响，具体误差参数如表3所示。在设计针轮针齿时，针齿半径上下公差都为负，因此表3中针齿半径误差取负值，针齿中心径向误差取负取正皆可。

表3 针齿销的误差参数

在坐标系xcOcyc中，含有移距修形误差△rp、等距修形误差△rrp和针齿半径误差△rrc的摆线齿廓曲线方程为：

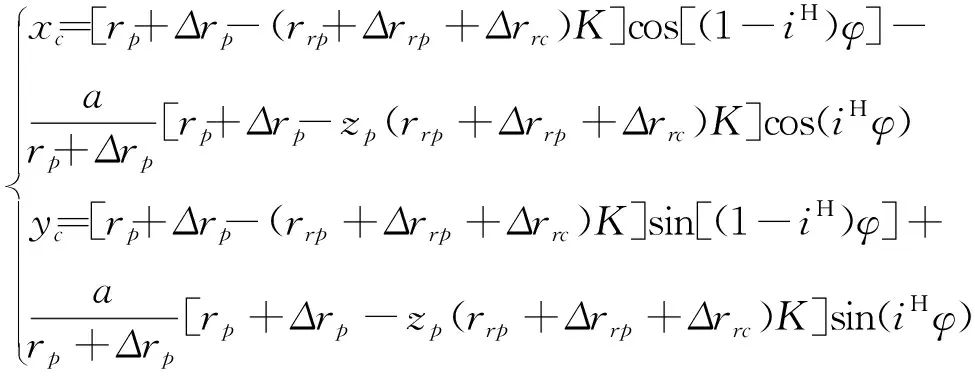
(2)

在坐标系xcOcyc中，含有针齿中心径向误差△rc的针齿中心圆的曲线方程为：

xp=(rp+Δrc)cosγ2-a

yp=(rp+Δrc)cosγ2

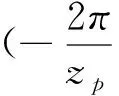
(3)

在式(2)、式(3)中，(xc,yc)为摆线轮齿廓曲线坐标；(xp,yp)为针齿中心圆曲线坐标；其他参数的含义同式(1)。

由上述方程式可以生成含有误差的摆线轮齿廓曲线和针轮中心圆曲线，从而建立摆线针轮副的误差模型。

1.3 有限元模型的建立

将PRO/E中建立的摆线针轮副模型，保存为stp格式导入到ABAQUS中定义接触分析。

定义材料属性，分别对摆线齿、针齿进行网格划分，采用全六面体网格，细化接触区域网格，对每一对齿进行同样操作，网格局部示意图如图3所示。分别定义摆线齿接触面39个，针齿接触面40个，使用面面接触。按照接触主从面的定义原则，面积较小、网格密度小的针齿接触面为从面，而面积较大、网格较粗的摆线齿接触面为主面。所有摆线齿、针齿接触面如图4所示。定义摩擦系数f=0.1，能量转化系数为0.9，能量分配系数为0.5。

图3 摆线轮与针轮局部网格图

图4 所有接触对示意图

针齿外圈施加全约束；摆线轮内圈节点在柱面坐标系下，施加径向(UX)和轴向(UZ)位移约束；将内圈节点与摆线轮内圈圆心耦合，并施加角速度ωH。约束及载荷施加情况如图5所示。

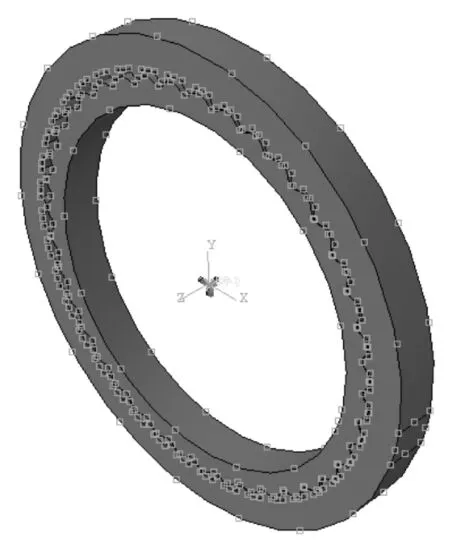
图5 约束及载荷施加情况

2 摆线针轮副接触分析

通过有限元分析，考察参与承载的摆线轮齿的齿面接触应力，传动过程中摆线轮与针轮的温度变化，并与理论计算结果比较，得出一定的规律。

2.1 摆线针轮副接触理论计算

2.1.1 摆线轮与针轮的受力分析

摆线轮针轮副在实际啮合过程中，针齿相对于摆线轮做连续的啮合运动，不仅局限于一个相对位置，而是连续周期性的啮合，每个齿上的啮合作用力均指向瞬心P，其受力如图6所示，理论上摆线轮有一半齿参与啮合。

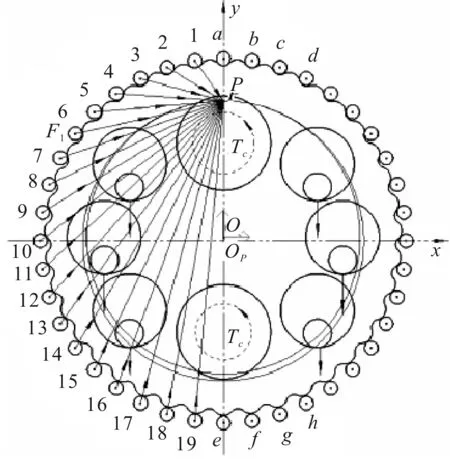
图6 摆线针齿啮合模型

设传递载荷时，对摆线轮所加力矩为Tc。在Tc的作用下，由于摆线轮与针轮齿的接触变形，摆线轮转过一个β角。传统摆线传动中，接触变形与针齿销弯曲变形的总和δi=βli。假定针齿啮合作用力Fi与总变形δi成线性正比关系，每个针齿对应的力臂li可以通过三角函数关系求出，则各齿上啮合作用力为：

(4)

式中：φi为针齿相对于针轮中心圆圆心的转角，即啮合相位角。

2.1.2 摆线齿与针齿齿面接触应力计算

在研究教育财政经费支出对(与)经济增长状况关系中，常用以下3种指标：一是教育财政经费支出占国内生产总值(GDP)的比例；二是教育财政经费支出占国民生产总值(GNP)的比例；三是教育财政支出占财政支出的比重。其中，教育财政经费支出占GDP或GNP的比例是反映和评价一个国家(或地区)高等教育投入水平的通用指标，是高等教育财政支出相对规模的重要标志。本研究选用的指标是教育财政经费支出占地区GDP的比例。

摆线齿齿廓是曲线，针齿齿廓是圆，当摆线齿与针齿啮合传动时，可以近似地看作两个瞬时圆柱体在接触。因此，摆线齿与针齿间的齿面最大接触应力σH、啮合处摆线轮实际齿廓曲线的当量曲率半径以及接触区产生的宽度可以依据赫兹公式近似计算，平均接触应力σp也可以计算出来。

根据赫兹公式，齿面接触应力可按式(5)计算：

(5)

式中：Ec为当量弹性模量，Ec=2E1E2/(E1+E2)，E1、E2分别为摆线轮与针齿的弹性模量，因摆线轮与针齿均为GCr15SiMn，故Ec=206 000 MPa；Fi为针齿与摆线轮某一位置啮合时的作用力，前面已求出；ρi为摆线轮在φi处的实际齿廓曲线的当量曲率半径。

以表1中的参数，设计摆线轮与针轮的标准模型及误差模型并进行计算。将设计参数代入式(4)和式(5)，可得到摆线轮齿与针齿的啮合作用力及摆线轮齿齿面上的最大接触应力。

2.2 无误差摆线针轮副接触分析

(1)摆线轮齿齿面接触应力云图。分别选取了摆线轮3号齿在0.025 s、0.050 s、0.100 s、0.125 s 4个时刻的齿面接触应力云图，如图7所示。

图7 摆线轮3号齿在不同时刻的齿面接触应力云图

从图7中可以看到，摆线轮3号齿在0.025 s时开始进入第一次啮合，0.125 s时进入第二次啮合。在0.025～0.125 s之间，接触区域从左逐渐向右移动，接触区域呈带状，区域中间接触应力较大，摆线齿齿面接触应力先增大后减小，0.100 s时接触应力最大，值为306.6 MPa。

(2)摆线轮某齿齿面接触应力沿齿廓、齿宽方向变化规律。分别沿齿廓、齿宽方向提取摆线轮三号齿在0.100 s这一时刻的齿面接触应力值，如图8所示，以便观察齿面接触应力沿齿廓、齿宽方向的变化规律。

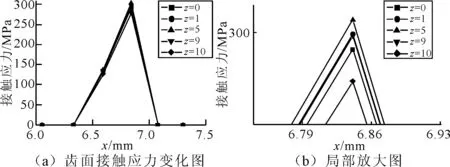
图8 摆线轮3号齿在0.100 s时齿面接触应力沿齿廓方向变化

图9提取了齿廓方向x=6.593 03 mm和x=6.842 06 mm上的齿面接触应力值。由此可以看出，x=6.842 06 mm处的接触应力大于x=6.593 03 mm处的接触应力，接触中间区域的应力大于边缘区域。

图9 摆线轮3号齿在0.100 s时齿面接触应力沿齿宽方向变化

(3)某时刻摆线轮某齿齿面Mises应力沿齿宽方向变化规律。分别选取了摆线轮1、2、3、4、5号齿在0.100 s时沿齿宽方向的齿面Von Mises应力值，如图10所示。

图10 摆线轮齿面Mises应力沿齿宽方向变化

Von Mises应力分布表明，摆线齿两端应力大于中间应力，即应力分布不均。

(4)某时刻针轮某齿齿面Mises应力沿齿宽方向的变化规律。分别选取了针轮1、2、3、4、5号齿在0.100 s时沿齿宽方向的齿面Von Mises应力值，如图11所示。

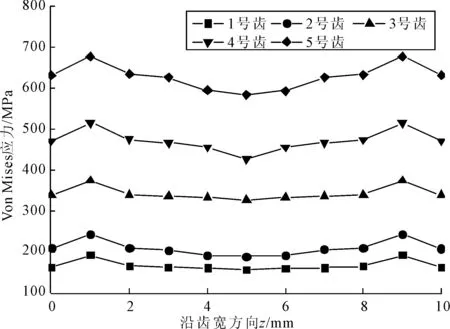
图11 针轮齿面Mises应力沿齿宽方向变化

Von Mises应力分布表明，针齿齿根弯曲应力分布不均，两端呈现骆驼峰分布，两端应力大于中间应力。

(5)某时刻摆线轮19对齿齿面接触应力比较。将摆线轮1～19号齿齿面接触应力的有限元模拟值和理论计算值进行对比，如图12所示。

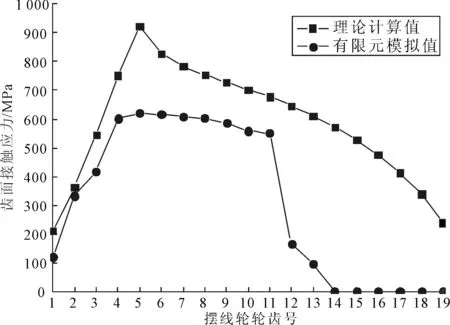
图12 摆线轮1～19号齿齿面接触应力

有限元模拟有13对齿参与承载，曲线整体符合先增后减的规律，最大接触应力发生在5号齿，与理论计算结果的变化规律趋于一致。

(6)摆线轮、针轮最大接触应力随时间的变化规律。从0～0.5 s之间，每隔0.005 s提取摆线轮、针轮轮齿齿面最大接触应力值，结果如图13所示。

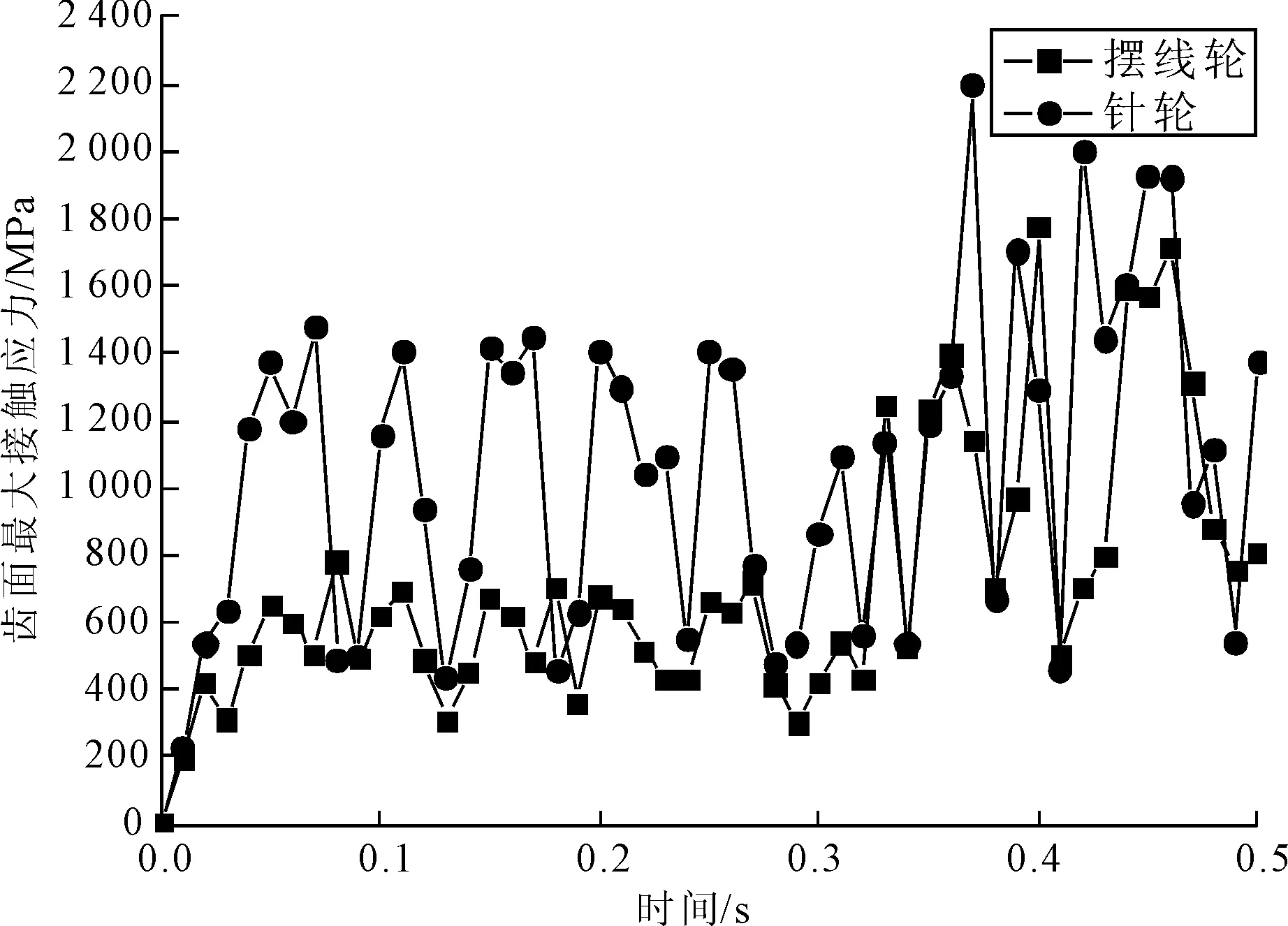
图13 摆线轮、针轮最大接触应力随时间的变化曲线

从图13可以看出，最大接触应力随时间整体呈现增长趋势，针轮接触应力整体大于摆线轮。

2.3 不同误差下摆线针轮副接触分析

2.3.1 不同误差对摆线轮最大接触应力的影响

(1)移距误差。图14为移距误差在0～0.5 s内对摆线轮齿面最大接触应力的影响规律。从图14可以看出，负移距误差的模型相比无误差模型，摆线轮齿面最大接触应力略减小；移距误差越大，摆线轮齿面接触应力越大。

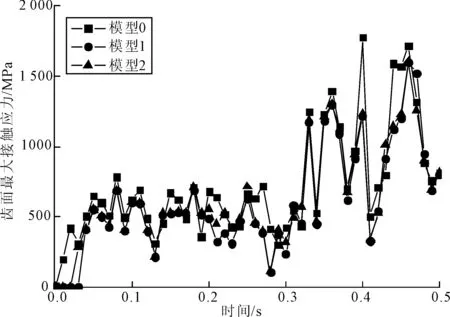
图14 移距误差对摆线轮齿面最大接触应力的影响规律

(2)等距误差。图15为等距误差在0～0.5 s内对摆线轮齿面最大接触应力的影响规律。从图15可以看出，正等距误差的模型相比无误差模型，齿面最大接触应力的变化趋势基本保持一致，并且等距误差的增大也没有使齿面最大接触应力出现明显的增大。

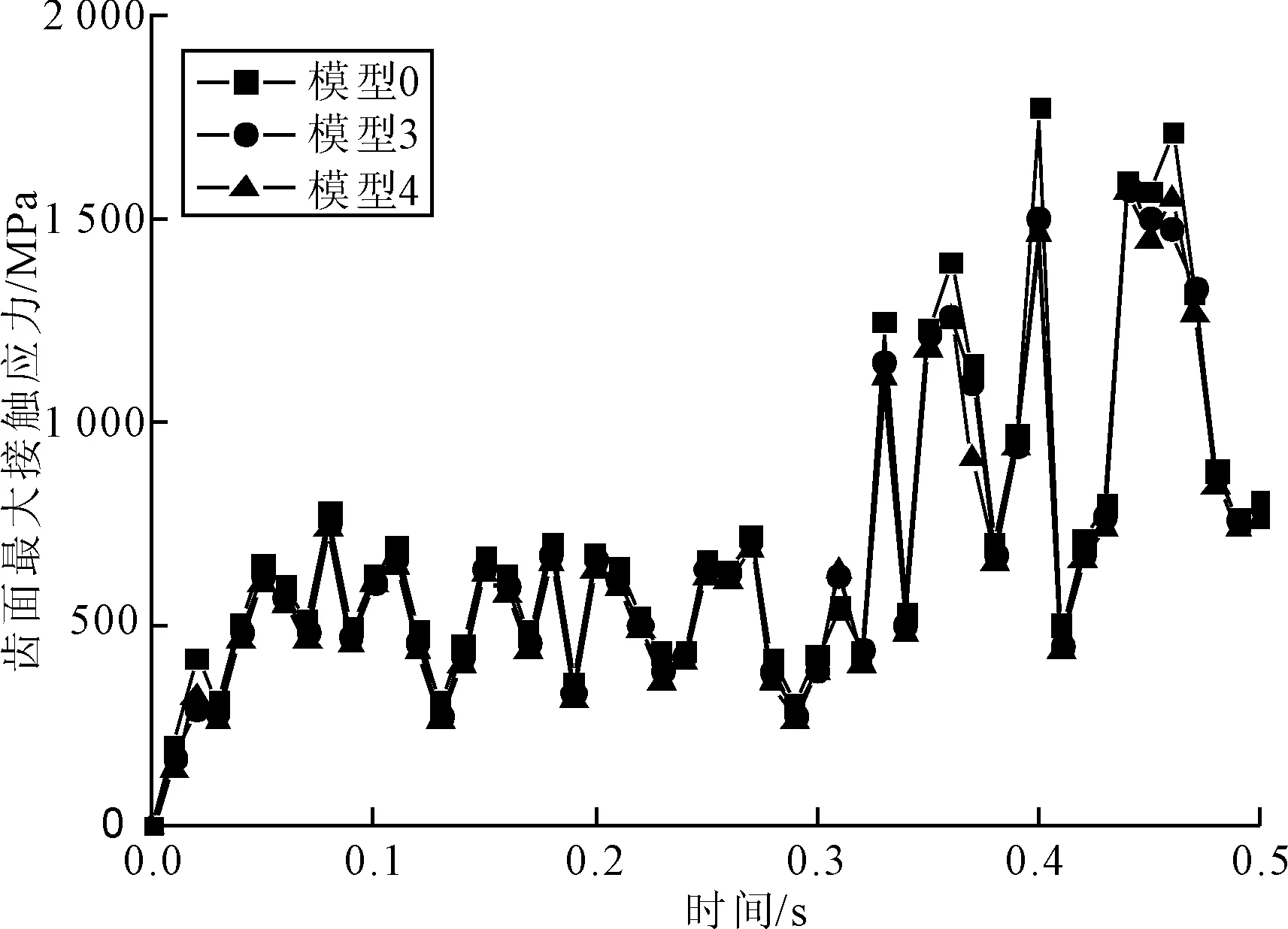
图15 等距误差对摆线轮齿面最大接触应力的影响规律

(3)移距误差+等距误差。图16为移距误差+等距误差在0～0.5 s内对摆线轮齿面最大接触应力的影响规律。从图16可以看出，正移距误差+正等距误差模型相比无误差模型，摆线轮齿面最大接触应力明显减小；等距误差相同的情况下，移距误差增加，摆线轮齿面最大接触应力值增大。

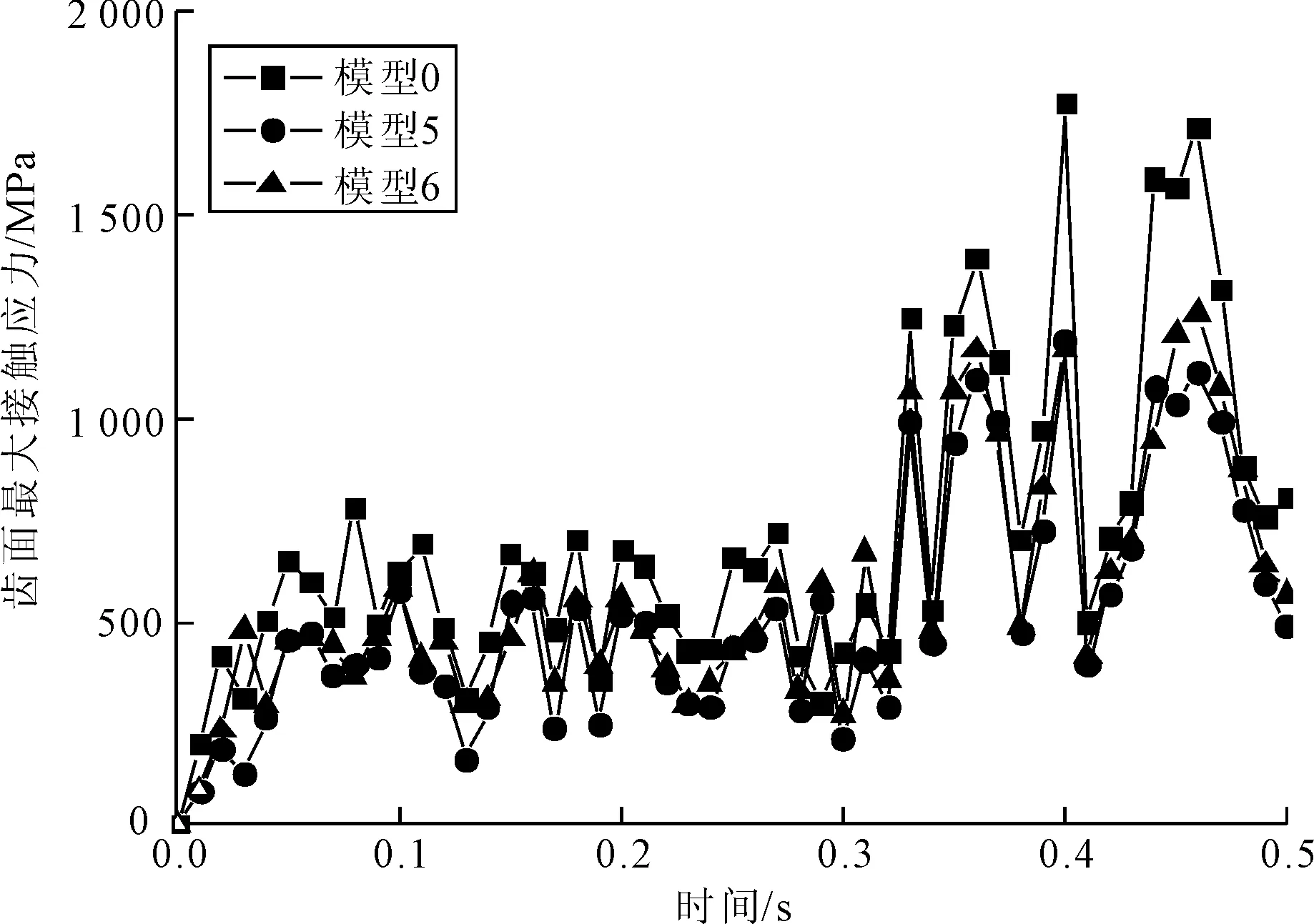
图16 移距误差+等距误差对摆线轮齿面最大接触应力的影响规律

(4)针齿半径误差。图17为针齿半径误差在0～0.5 s内对摆线轮齿面最大接触应力的影响规律。从图17可以看出，含针齿半径误差的模型相比无误差模型，前0.050 s接触区域较大，摆线轮齿面最大接触应力先减小，0.050 s之后接触区域较小，摆线轮齿面最大接触应力而后增大；针齿半径误差越大，摆线轮齿面接触应力反而越小。

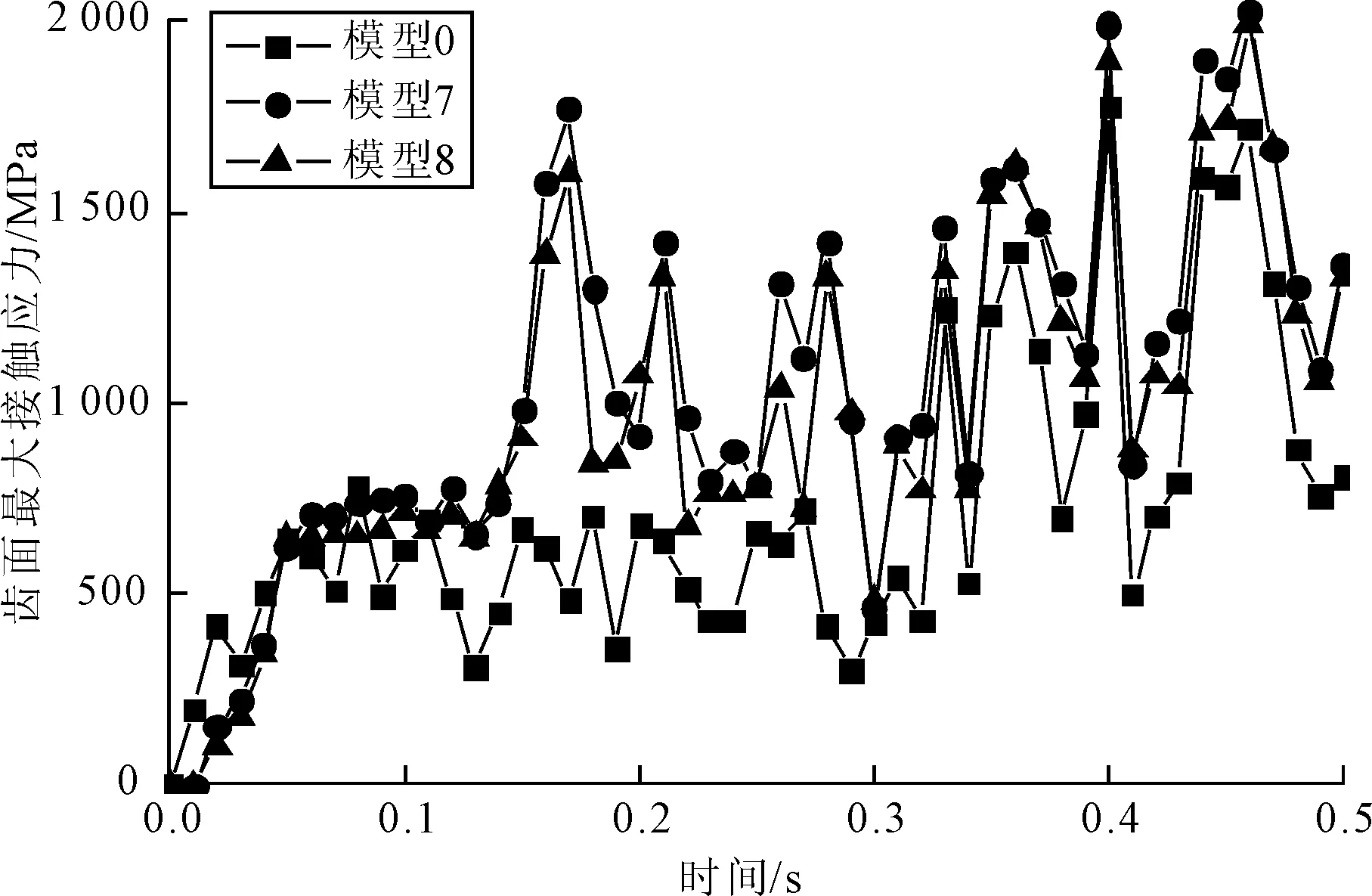
图17 针齿半径误差对摆线轮齿面最大接触应力的影响规律

(5)针齿中心径向误差。图18为针齿中心径向误差在0～0.5 s内对摆线轮齿面最大接触应力的影响规律。从图18可以看出，负针齿中心径向误差的模型相比无误差模型，摆线轮齿面最大接触应力略微减小；正针齿中心径向误差的模型相比无误差模型，摆线轮齿面最大接触应力明显增大。针齿中心径向误差越大，摆线轮齿面最大接触应力值越大。

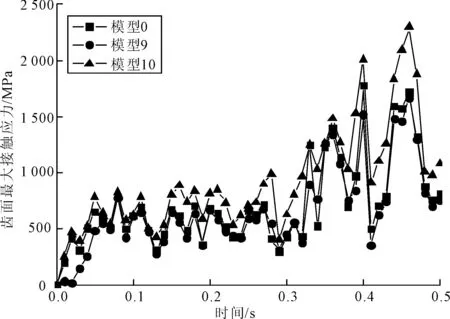
图18 针齿中心径向误差对摆线轮齿面最大接触应力的影响规律

(6)针齿半径误差+针齿中心径向误差。图19为针齿半径误差+针齿中心径向误差在0～0.5 s内对摆线轮齿面最大接触应力的影响规律。从图19可以看出，针齿半径误差+针齿中心径向误差的模型相比无误差模型，前0.150 s摆线轮齿面最大接触应力变化趋势基本一致，0.150 s之后摆线轮齿面最大接触应力明显增大；正针齿中心径向误差的模型相比负针齿中心径向误差的模型，摆线轮齿面最大接触应力值增大。

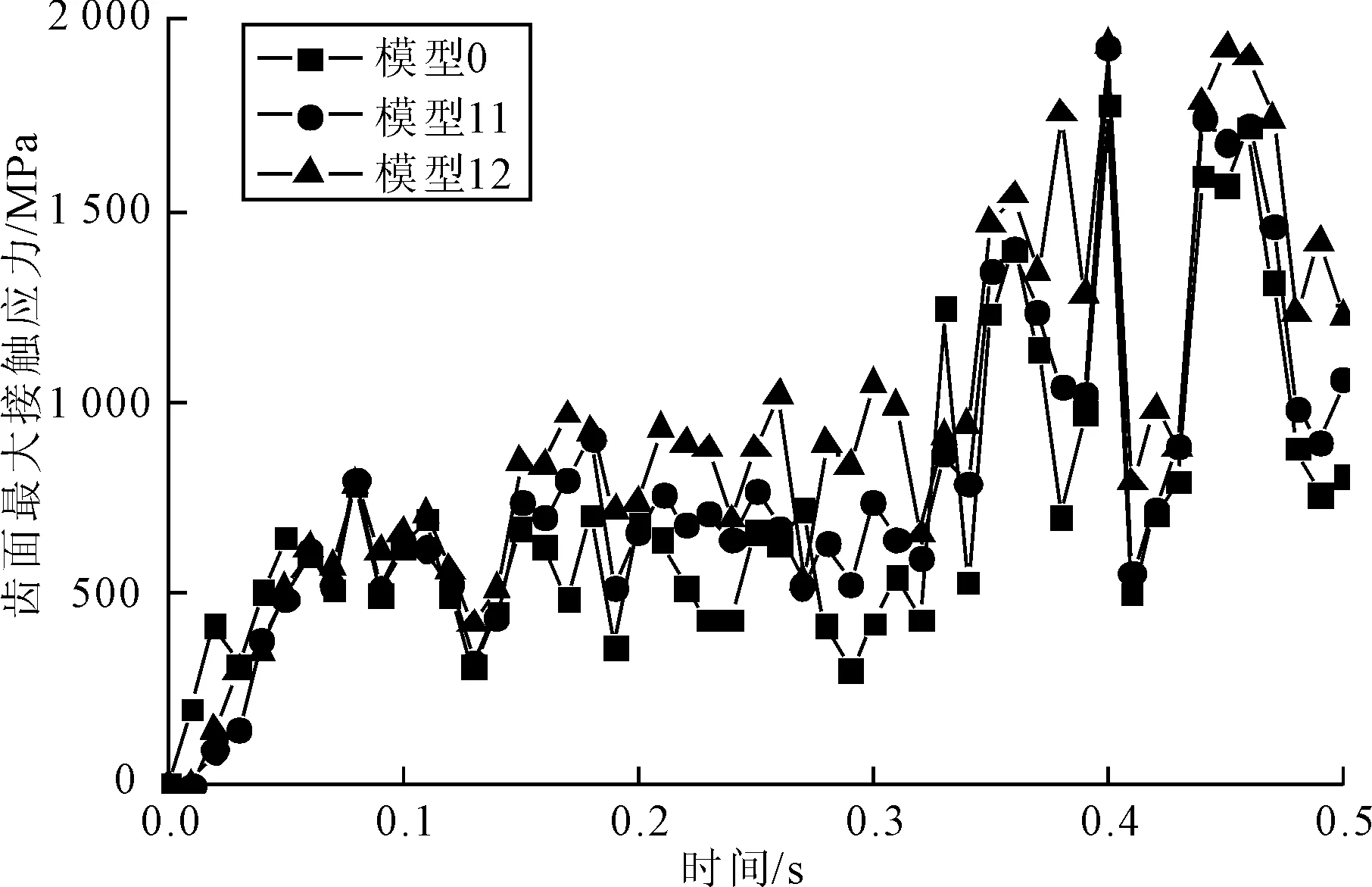
图19 针齿半径误差+针齿中心径向误差对摆线轮齿面最大接触应力的影响规律

2.3.2 不同误差对针轮最大接触应力的影响

(1)移距误差。图20为移距误差在0～0.5 s内对针轮齿面最大接触应力的影响规律。从图20可以看出，负移距误差的模型相比无误差模型，针轮齿面最大接触应力略减小；移距误差越大，相应地针轮齿面接触应力值越大。

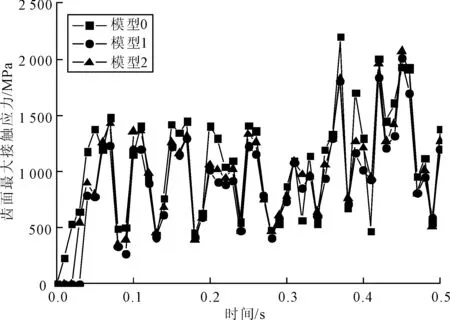
图20 移距误差对针轮齿面最大接触应力的影响规律

(2)等距误差。图21为等距误差在0～0.5 s内对针轮齿面最大接触应力的影响规律。从图21可以看出，正等距误差的模型相比无误差模型，针轮齿面最大接触应力稍减小；等距误差越大，针轮齿面接触应力值越小。

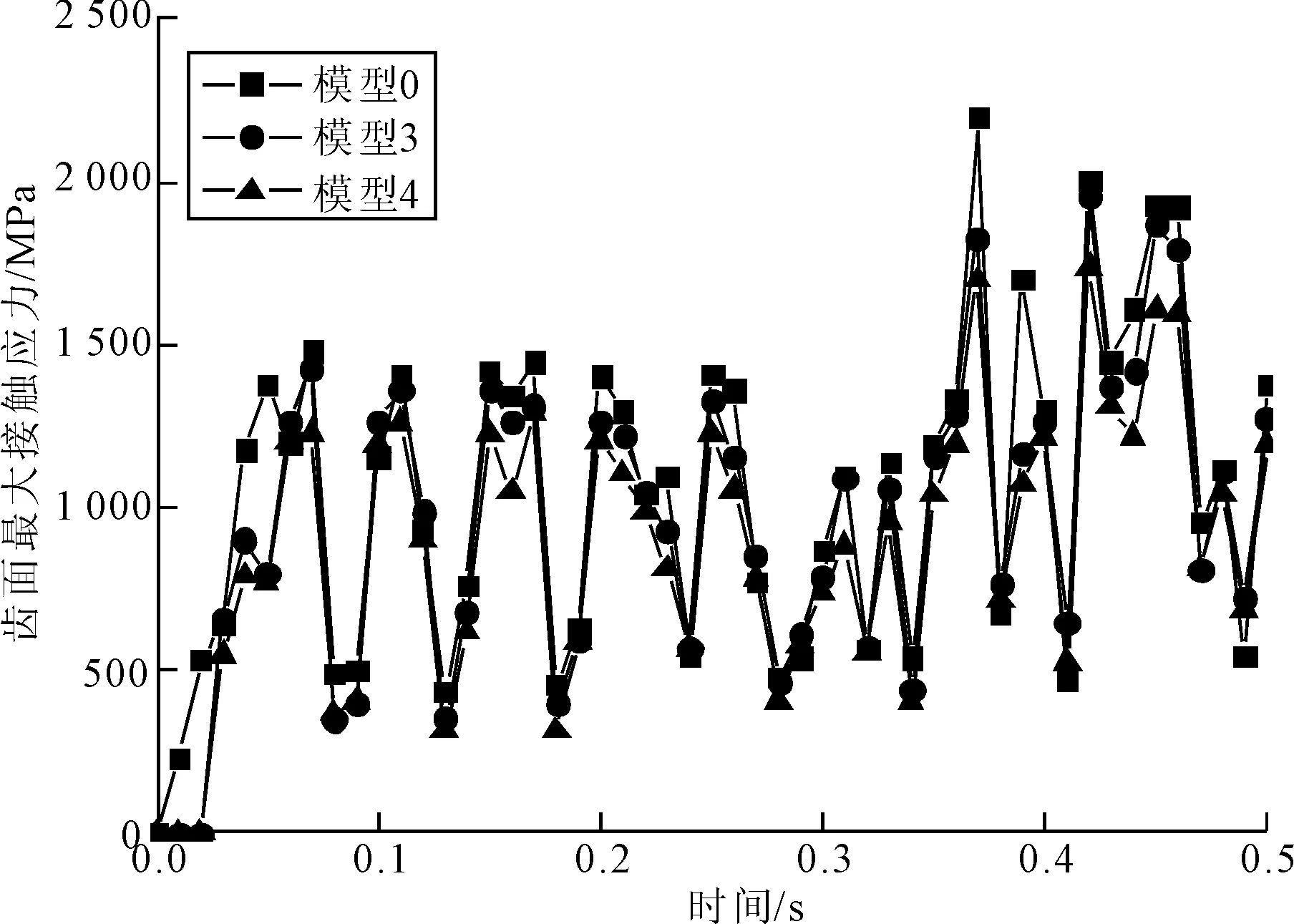
图21 等距误差对针轮齿面最大接触应力的影响规律

(3)移距误差+等距误差。图22为移距误差+等距误差在0～0.5 s内对针轮齿面最大接触应力的影响规律。从图22可以看出，移距误差+等距误差的模型相比无误差模型，针轮齿面最大接触应力明显变小；等距误差相同的情况下，移距误差越大，针轮齿面最大接触应力值越大。

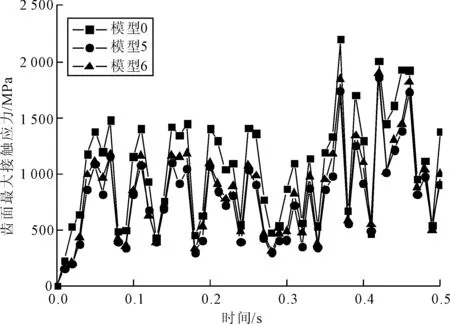
图22 移距误差+等距误差对针轮齿面最大接触应力的影响规律

(4)针齿半径误差。图23为针齿半径误差在0～0.5 s内对针轮齿面最大接触应力的影响规律。从图23可以看出，针齿半径误差的模型相比无误差模型，针轮齿面最大接触应力明显增大；针齿半径误差越大，针轮齿面接触应力值越小。

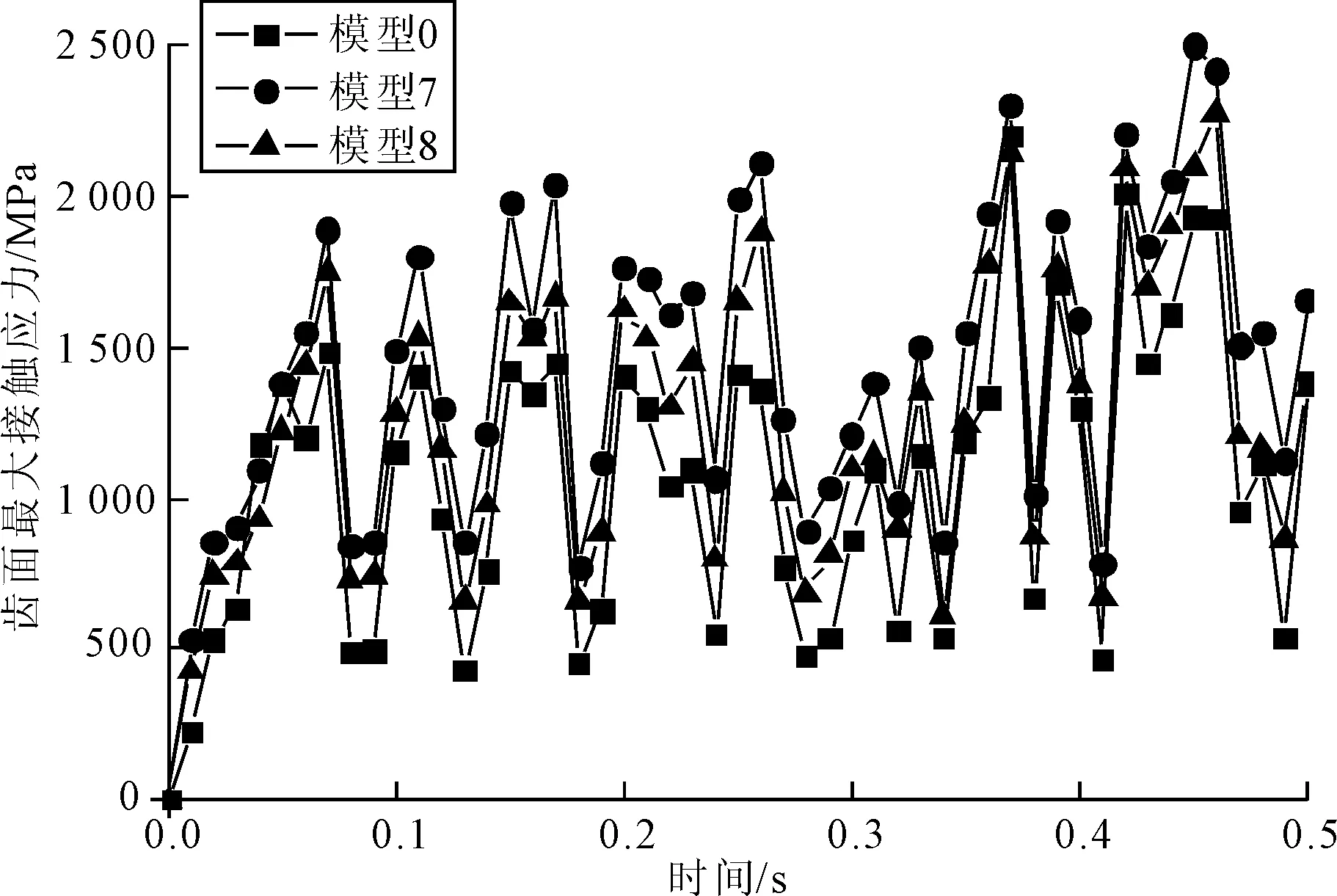
图23 针齿半径误差对针轮齿面最大接触应力的影响规律

(5)针齿中心径向误差。图24为针齿中心径向误差在0～0.5 s内对针轮齿面最大接触应力的影响规律。从图24可以看出，负针齿中心径向误差的模型相比无误差模型，针轮齿面最大接触应力明显变小；正针齿中心径向误差的模型相比无误差模型，摆线轮齿面最大接触应力明显变大。因此，针齿中心径向误差越大，针轮齿面最大接触应力值越大。

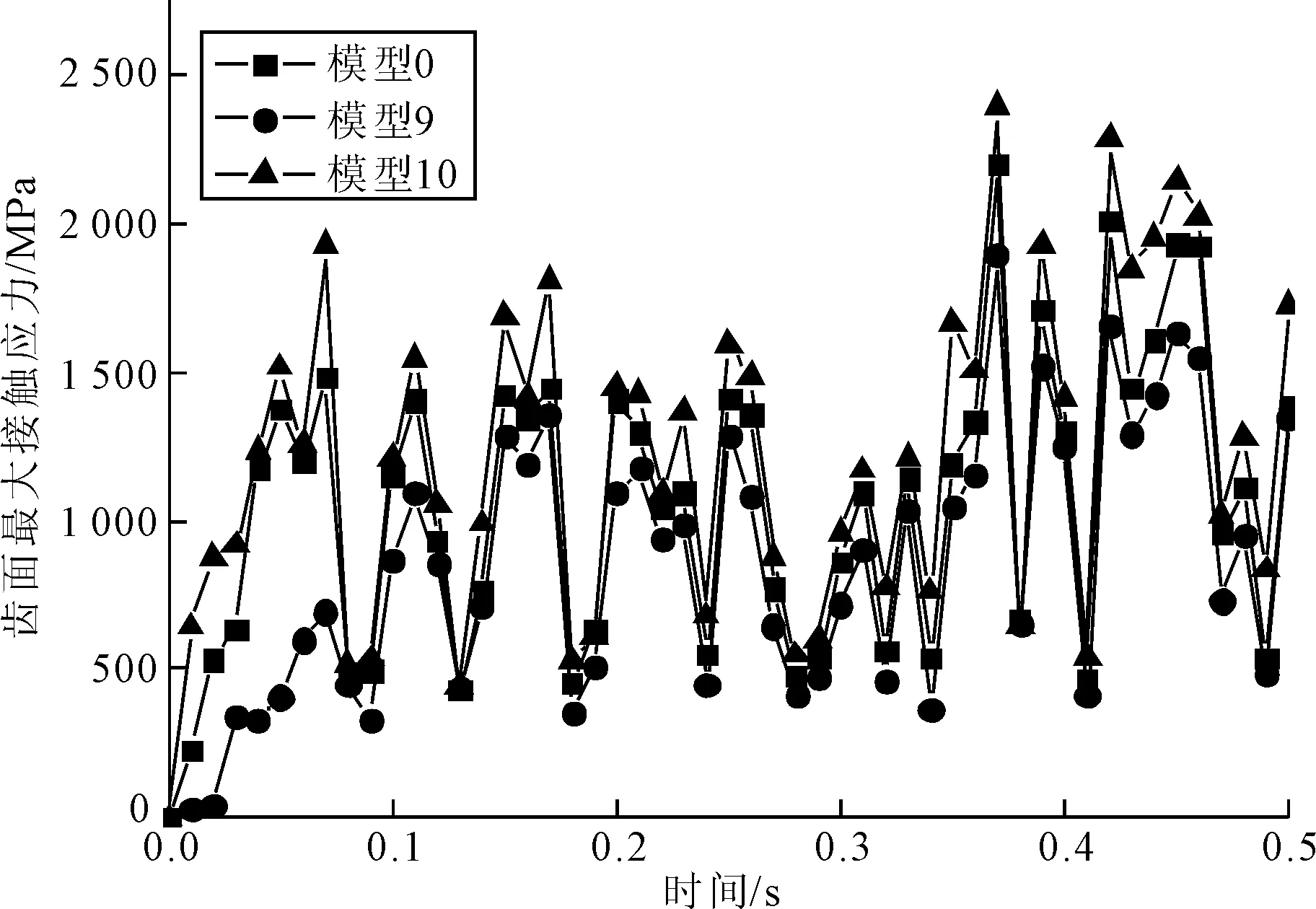
图24 针齿中心径向误差对针轮齿面最大接触应力的影响规律

(6)针齿半径误差+针齿中心径向误差。图25为针齿半径误差+针齿中心径向误差在0～0.5 s内对针轮齿面最大接触应力的影响规律。从图25可以看出，针齿半径误差+针齿中心径向误差的模型相比无误差模型，针轮齿面最大接触应力略大；正针齿中心径向误差的模型相比负针齿中心径向误差的模型，针轮齿面最大接触应力值略大。

图25 针齿半径误差+针齿中心径向误差对针轮齿面最大接触应力的影响规律

3 结论

(1)建立了含摆线轮齿廓误差和针齿销误差的摆线针轮副接触模型，计算了摆线齿齿面接触应力，有限元计算结果和理论计算结果比较吻合，验证了模型的有效性。

(2)通过有限元模拟计算，揭示了同种误差对摆线针轮副接触的影响规律。移距误差越大，摆线轮、针轮接触应力越大；等距误差对摆线轮、针轮接触应力影响较小，等距误差越大，针轮接触应力越小；针齿半径误差越大，摆线轮、针轮接触应力越小；针齿中心径向误差越大，摆线轮、针轮接触应力越大。

(3)通过有限元模拟计算，揭示了不同误差对摆线针轮副接触的影响程度。研究结果表明，针齿半径误差对齿面接触应力的影响最大，针齿中心径向误差的影响较大，移距误差次之，等距误差影响最小。

参考文献：

[1] 日高照晃.サイクロイド歯輪を用いたK-H-V形游星歯輪装置の回転伝運誤差に関する研究(第1報,解析方法)[C]∥日本機械學會論文集,1994,60(570):645-653.

[2] 石田武.サイクロイド歯輪を用いたK-H-V形游星歯輪装置の回転伝運誤差に関する研究(第2報,各种の加工误差·组立误差が回転传达误差に及ぼす影响)[C]∥日本機械學會論文集,1994,60(578):278-285.

[3] 王宏猷.サイクロイド歯輪を用いたK-H-V形游星歯輪装置の回転伝運誤差に関する研究(第3報,各种误差にょる相互影响)[C]∥日本機械學會論文集,1994,60(578):286-293.

[4] Manfred C, Antoni J. FEM in Numerical Analysis of Stress and Displacement Distributions in Planetary Wheel of Cycloidal Gear[C]∥ Numerical Analysis and It’s Applications Second International Conference. [S.l. ]:[s.n.],2000:772-779.

[5] Bobach L, Beilicke R, Bartel D, et al. Thermal Elastohydrodynamic Simulation of Involute Spur Gears Incorporating Mixed Friction[J]. Tribology International, 2012,48:191-206.

[6] 王文涛.RV减速器热-结构耦合分析[D].北京：北方工业大学,2016.

[7] 姚灿江,魏领会,王海龙,等.RV减速器摆线轮动态接触应力有限元分析[J].煤矿机械,2016,37(6):76-78.

[8] 冉毅.RV减速器传动精度分析[D].重庆：重庆大学,2015.

[9] 魏波,周广武,杨荣松,等.RV减速器摆线轮齿廓修形方法对比研究[J].机械设计与研究,2016,32(1):41-47.

[10] 齿轮传动设计手册[M].北京:化学工业出版社,2005.

[11] 机械设计手册[M].北京:化学工业出版社,2002.