特种高效填料用于13C分离的计算传质学研究

田叶盛，李虎林

(上海化工研究院有限公司 上海稳定性同位素工程技术研究中心，上海 200062)

碳-13同位素具有稳定的物理化学性能，广泛应用于生物化学、医药学及临床诊断等领域。随着医疗诊断领域同位素呼吸实验的快速发展，对稳定同位素13C的需求与日俱增。现阶段，低温精馏法是分离制备高丰度13C的唯一工业化方法。国际上普遍采用高比表面积散堆填料进行13C同位素的分离，主要有Dixon环、Heli-pak、前苏联梯比利斯科学研究所采用的三角螺旋圈、美国Cola-Colita装置采用的Propak填料[1-3]等。虽然散堆填料具有比较高的分离效率，但其阻力压降大，操作弹性小，塔内液相流体沿填料表面向下流动时，易形成壁流和沟流，放大效应影响显著，在工业化运用中，装置的实际生产能力低于初始的设计生产能力，美国Los Alamos实验室于1978年建立了一座CO低温精馏分离13C工厂，设计产能达到年产20 kg13C同位素，而实际运行产出13C同位素仅为年产8 kg。随着规整填料塔技术及相关低温科学的长足发展，为13C分离塔的工业放大提供了技术基础。为此，上海化工研究院自主研发了新型高比表面积规整填料PACK-13C[4-5]，兼具散堆填料和规整填料的优点，用于低温精馏分离13C的工业实验。与国外低温精馏塔装置相比，PACK-13C规整填料低温精馏装置具有较低的阻力降、较大的操作弹性，且装置的放大效应远低于散堆填料塔。但如何准确预测低温精馏规整填料塔的传质性能，降低工业化的风险，仍是研究者们亟需探索和十分关注的问题。通常情况下，利用经验和半经验理论，选取基于全塔操作的变量作为预测整塔传质效率的变量因素，如进料量、物料组分、塔顶操作压力、塔釜温度等。在实际操作过程中，规整填料塔内气液传质过程涉及到复杂的多尺度流体流动和传质现象，不同的流动形态和分布也是影响塔传质性能的关键因素，现有的经验、半经验方法无法从气液相互作用的本质进行整塔传质效率的预测，会造成规整填料塔传质性能预测的较大偏差。为实现准确预测13C分离用低温精馏塔的传质效率，减少工业化风险，本文通过对PACK-13C高效填料在低温精馏塔内的计算传质学研究，提出一种耦合传质效率的计算流体力学方法(CFD)，实现由局部精馏单元的传质模拟计算推广到对整塔传质性能的模拟预测，该方法可为解决同位素分离装置的放大效应、实现工程化突破提供理论依据和指导。

1 低温精馏分离13C同位素的流程

低温精馏法分离制备稳定同位素13C的工艺流程示于图1，可分为四个组成部分，除低温精馏塔外，还有原料气净化系统、蒸发系统和冷凝系统。一氧化碳原料气经过净化处理后进入低温精馏塔，在塔顶冷凝器内被液氮冷凝成液体，沿着塔内规整填料表面向下流动，且与上升的气流相互作用，实现同位素的交换和聚集。流到塔底的液体被再沸器系统加热气化，使得塔内形成持续的上升气流与下降的液相进行相互作用，经过不断的气液交换后，其中的重组分13CO同位素分子将在塔底得到富集，而轻组分12CO分子在塔顶实现富集，以此实现同位素的分离。

上海化工研究院先后建立了低温精馏分离13C同位素的小试和中试实验装置[6]，用于各种填料的开发及性能测试。本文通过计算传质学方法进行填料设计，在建立的小试装置上进行实验。

图1 低温精馏分离碳同位素单塔实验流程图Fig.1 Schematic of cryogenic distillation single tower for carbon isotope separation

2 PACK-13C规整填料精馏单元的建立

设计的PACK-13C波纹填料，其规格为波纹倾角45°，峰高2.5 mm，波距4 mm，端面为等腰三角形。实验条件列于表1，塔顶绝对压力60 kPa，塔顶温度为77 K。由于计算传质学相关理论及现有计算机处理能力的限制，目前还无法对整塔，甚至整盘填料进行精确的数值模拟计算。运用多尺度计算传质学方法与局部平均概念，选取精馏塔内的两片填料片，该两片填料构成一组精馏单元，以此进行模拟研究[7-8]。该方法通过模拟更加真实的填料精馏单元内气液两相相互传质行为，由此推广运用于整塔传质，简化过程示于图2。该精馏单元模型由两片规整填料片构成，模型宽0.02 m，高为0.05 m，模型的结构尺寸为上述所述PACK-13C填料尺寸。

表1 低温精馏实验条件表Table 1 Cryogenic distillation experimental conditions

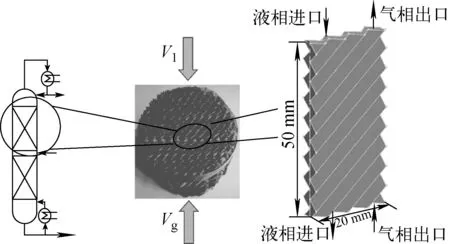
图2 PACK-13C规整填料精馏单元传质计算模型简化过程Fig.2 Simplified process of mass transfer calculation model for PACK-13C structured packing distillation unit

当液相进口为均匀初始分布时，且假设填料内无支撑和分布器等其他元件的影响时，填料内部只存在孔道相互交叉引起的流体局部不均匀分布，以此可认为与该传质计算模型相平行的各流域内的流场分布相同。因此只需计算由两片填料组成的局部单元内部的流场信息，获得规整填料局部液相传质系数和局部气相传质系数。

3 流体力学控制方程

在精馏过程中，气液两相流体在规整填料表面相互作用，实现轻重组分的相互分离。因此为了跟踪考察填料表面上气液两相的相界面，选取两相流模型中的VOF模型对规整填料精馏单元进行非稳态数值模拟。考虑到相界面的湍动效应，该模型选用RNG(renormalization group)k-ε湍流模型(重整化群k-ε模型)描述液相流体在填料空间内的流动过程[9-10]。其控制方程动量源项中主要考虑重力源项和表面张力源项，具体方程如下：

(1)

(2)

(3)

(4)

采用重整化群k-ε双方程湍流模型封闭雷诺时均方程，以下即为k和ε运输方程：

Gk+Gb-ρε-YM

(5)

(6)

上述方程中，Gb表示由于浮力影响引起的湍动能生成项，在等温过程时，Gb=0；YM表示可压速湍流脉动膨胀对总的耗散率的影响，在本文计算中，流体假设为不可压缩，因此此项可忽略不计。C1ε、C2ε、C3ε为RNGk-ε模型常数，C1ε=1.44，C2ε=1.92，C3ε=1.42；Gk表示由于平均速度梯度引起的湍动能生成项，Gk=μtS2，其中S是平均应力张量系数，可表示为：

(7)

(8)

式(1)～(8)中，ρ为流体密度，kg/m3；ui为第i相(气相或液相)速度值，m/s；P为压力，Pa；Fi为第i相的动量源项，N/m3；μ为动力粘度，kg/(m·s)；μt为涡流粘度，kg/(m·s)；k为湍动动能，N·m；ε为湍流耗散率，N/s；μeff为RNG模型中的有效粘度，kg/(m·s)；α为体积分率。

4 规整填料计算传质学分析

规整填料计算传质学分析的基本思路是在流体力学计算的基础上，结合经典的气液传质理论BRF模型，得到一种耦合传质效率的CFD计算方法，具体为：通过对图2所示精馏单元CFD模型进行流体力学模拟计算，获得填料孔道内的局部气、液相流场信息。在此基础上，采用经典的气液传质理论BRF模型预测局部的传质效率，进而估算整塔的传质效率。

4.1 规整填料局部液相传质系数

根据渗透理论，依据BRF模型提出的液相传质系数的计算关系式，运用计算流体力学模拟得到规整填料的局部液相传质系数：

(9)

4.2 规整填料局部气相传质系数

气相传质系数可由舍伍德(Sherwood)准数求得，如公式(10)所示。规整填料单元的局部气相传质系数可由局部的气、液相速度计算，其中，气相速度UGe和液相速度ULe可结合计算流体力学CFD模拟求得。

(10)

(11)

4.3 规整填料等板高度HETP

利用传统的双膜理论，将局部气、液传质系数以及气液流动参数代入公式(12)～(16)中，求取规整填料的局部等板高度HETP。

(12)

(13)

(14)

(15)

(16)

5 边界条件与初始条件

5.1 气液相进口条件

采用速度入口边界，主要设置入口处气液相的速度大小和方向。利用Nusselt理论设置流体的入口速度分布，均为均匀初始分布。给定液相入口速度，流体内不包含气相组分，其湍流强度为0.5%，水力直径为2 mm。气相入口处的流体不包含液相组分，其湍流强度为1%，水力直径为5 mm。

5.2 气液相出口条件

气液相出口处均为完全发展流动，在确定的计算条件下，出流口按正常的大气压力，流体流出的边界条件按零速度梯度假定处理。

5.3 壁面条件

壁面条件用于限定流体的流动区域。本文采用重整化群k-ε模型描述液膜的流动过程，属于低Re数流体流动，且属于近壁流动，整个液膜计算域都受到近壁粘性底层的影响，因此需要修改湍流模型使之适用于近壁区粘性底层的计算。因此选用Fluent中“增强壁面处理法”描述这种受粘性底层影响较大的液膜流动。

5.4 初始条件

该模型初始时，假定计算域内不存在液相，只存在静止的气相，具体的初始条件如下：t=0，αG=1，αL=0。

6 数值求算方法

规整填料片结构复杂，且存在多个相互交叉的通道，生成均匀一致的结构化网格非常困难。将模型中每一个单元通道划分成四面体非结构化网格，采用精度较高的Geo-Reconstruct界面重建格式；将所有的网格设为在整个计算域内连续，网格总数为300 631个。采用有限元分析软件Ansys 19.0进行流体力学数值求解，该模拟过程为非稳态过程，时间项采用隐式格式；压力项采用PRESTO！算法；压力-速度耦合方式采用PISO算法；动量方程的离散格式采用一阶迎风格式；时间步长选取10-5s。

7 结果与讨论

7.1 实验传质性能参数的测定

采用全回流实验条件，通过测定不同喷淋密度及气相负荷条件下低温精馏塔的塔顶和塔底的13C丰度，以此分析研究低温精馏塔内的传质过程。

由于实验在全回流条件下进行，可依据Fenske公式计算全塔的最小理论板数Nmin：

(17)

其中，分离系数α采用温度T(单位K)表示的公式计算：

(18)

根据物料衡算方程，原料气F0(mol/s)、塔顶尾气MT(mol/s)及塔底产品MW(mol/s)满足以下计算关系式：

F0=MT+MW

(19)

(20)

(21)

F0x0=MTxT+MWxW

(22)

HETP=H/Nmin

(23)

Wp=Nmin/H×F

(24)

式中，x0、xT和xW分别为原料气、塔顶尾气和塔底产品的13C浓度值，分别从原料、塔顶和塔底取样毛细管中取样分析所含13CO的丰度；H为填料塔填充的有效填料高度，m；F为气相动能因子，m·s-1·(kg·m-3)0.5；HETP为填料等板高度，m；Wp为填料分离功，s-1·(kg·m-3)0.5；进而求得不同实验条件下的等板高度传质数据，不同实验条件下测定的13C丰度及等板高度实验值列于表2。

表2 不同实验条件下测定的13C丰度及等板高度实验值Table2 The abundance of 13CO and the experimental of HETP on the different conditions

7.2 计算传质学模拟与分析

通过精馏单元传质计算模型(图2)，运用多尺度的计算传质学方法，对分离13C同位素用低温精馏塔进行传质学研究，分别获得了表征低温精馏塔传质性能的等板高度及分离功的模拟计算值。

等板高度(HETP)又称理论板当量高度，指一定高度的填料段分离效果与一层理论塔板或一个理论级相等，是衡量精馏塔传质性能的重要参数。运用式(9)～(16)对低温精馏塔等板高度进行模拟计算，并将模拟值与实验值汇总列于表3。

表3 等板高度模拟计算值与实验值比较Table 3 Comparison between the simulated value of HETP and the experimental value

分离功模拟计算值与实验值比较结果列于表4。在评价填料塔传质特性的研究中，分离功是表征填料分离能力的重要参数指标，综合体现了填料承载负荷的能力和分离效率，其值表明若完成一定分离任务时，所需要的填料体积大小。分离功越大，表明填料的分离能力越强，满足分离一定任务所需的填料体积越少。

由表3和表4结果可知，通过局部精馏单元传质计算推广得到的等板高度和分离功的模拟值与实验值吻合较好，等板高度的平均相对误差为10.15%，分离功的平均相对误差为9.1%。由此说明可以运用局部平均计算传质学方法，对整个精馏填料塔进行传质性能的预测和评估。等板高度模拟值相较于实验值均偏大，分离功模拟值相较于实验值均偏小，主要是由于建立的PACK-13C规整填料精馏单元计算模型的结构尺寸较小，且规整填料内部气液界面波动较为剧烈，这种界面效应能显著强化传质作用，而采用局部单元的传质模拟时忽略了气液界面扰动影响，使得模拟的填料传质性能低于实际情况，从而造成等板高度模拟值偏大，分离功模拟值偏小。

表4 分离功模拟计算值与实验值比较Table 4 Comparison between the simulated value of separation work and the experimental value

8 小结

本文提出了一种耦合传质效率CFD计算方法，运用该方法对自主开发的PACK-13C高效规整填料在低温精馏塔内的传质性能进行模拟研究，实现了由局部精馏单元的传质模拟计算推广到对整塔传质性能的预测，通过对13C分离用低温精馏整塔的等板高度和分离功模拟计算，可以较准确的实现全塔传质性能的预测和评估，该方法也为解决同位素分离装置的放大效应，实现13C同位素规模化生产的工程化突破提供了理论依据和方法指导。

参考文献：

[1] Johns T F, London H. Enrichment of isotopes13C and18O[R]. Harwell: Atomic Energy Research Establishment(AERE), G/R 661, 1951.

[2] Armstrong D E, Briesmeister A C, Mclnteer B B, et al. A carbon-13 production plant using carbon monoxide distillation[R]. New Mexico: Los Alamos National Laboratory, LA-4391, 1970.

[3] 杨国华,曾权兴. 稳定同位素分离[M]. 北京：原子能出版社,1989：212-262.

[4] Li Hulin, Ju Yonglin, Li Liangjun, et al. Separation of isotope13C using high-performance structuredpacking[J]. Chemical Engineering and Processing: Process Intensification, 2010, 49: 255-261.

[5] 李虎林. 低温精馏分离13C的耦合传递理论与试验研究[D]. 上海：上海交通大学，2011.

[6] 田叶盛，李虎林，姜永悦，等. 稳定同位素13C分离二塔级联耦合优化设计与实验研究[J]. 同位素，2016，29(3):152-157.

Tian Yesheng, Li Hulin, Jiang Yongyue, et al. Coupling optimization design and experimental study on stable isotope13C separation of the double-stage cascade[J]. Journal of Isotopes, 2016, 29(3): 152-157(in Chinese).

[7] 谷芳. 规整填料局部流动与传质的计算流体力学研究[D]. 天津: 天津大学,2004.

[8] Van Baten J M, Krishna R. Liquid-phase mass transfer within KATAPAK-SR structures studied using computational fluid dynamics simulations[J]. Catalysis Today, 2001, 69: 371-377.

[9] Petre C F, Larachi F, Iliuta I. Pressure drop through structured packings: Breakdowninto the contributing mechanisms by CFD modeling[J]. Chem Eng Sci, 2003, 58: 163-177.

[10] 王瑞金,张凯,王刚. FLUENT技术基础与应用实例[M]. 北京:清华大学出版社,2006.

[11] Bravo J L, Rocha J A, Fair J R. A comprehensive model for the performance of columnscontaining structured packings[J]. Inst Chem Eng Symp Ser, 1992, 128: A489.