基于H∞鲁棒控制的电动叉车稳定性研究

曹 勇， 肖本贤(1.合肥工业大学 工业与装备技术研究院，合肥 230009；2.合肥工业大学 电气与自动化工程学院，合肥 230009)

汽车在转弯时，由于内外轮转弯半径不一样，内外轮必须以不同的角速度旋转，传统车辆使用机械差速器实现这一功能[1]，而电动叉车作为工业搬运车辆的一种，广泛地应用在狭窄的车间、港口、车站等地方，相对于传统的汽车来说，对转向的要求更高.对于电动叉车来说，使用电子差速器来代替机械差速器，完成叉车的转向任务.

文献[2]采用阿克曼转角关系来约束左右车轮的转速，说明了转弯时转弯半径应该满足的几何关系;文献[3]采用了神经网络控制策略，根据获得的车速和转向角对左右轮进行转速控制，通过该方法提高了汽车的转向稳定性;文献[4]从垂直载荷的角度出发，以驱动轮附着率相等为目标，提出了基于垂直载荷的电子差速控制策略,并且在MATLAB下验证了该算法的有效性;文献[5]以无刷直流轮毂电机驱动后轮为研究对象，设计了一种鲁棒控制器，通过试验车验证了该控制器的有效性;文献[6]根据车辆纵向动力学模型,建立包括制动监视器、滑移率调节器, 并在MATLAB/Simulink和Car Sim进行联合仿真，仿真结果表明该方法有效地使滑移率确定在期望值,制动力矩输出连续,提高了电动汽混合制动的性能.电动叉车由于载货质量大，工况更复杂，外界干扰多，对于整车稳定性要求更高[7].由于鲁棒控制具有在一定的参数摄动下，维持系统某些性能的特性，这里对整车模型进行混合灵敏度H鲁棒控制设计，设计了一种鲁棒电子差速控制器，并在MATLAB/SIMULINK下进行了仿真验证，仿真结果表明，叉车在工况下的行驶稳定性得到了提高.

1 电动叉车七自由度整车模型

1.1 车体动力学模型

1.1.1 车辆坐标系

当叉车在平整的路面上保持静止时，以叉车的质心为坐标原点；X轴方向为叉车车头方向；Y轴方向为驾驶员左侧方向；Z轴方向是垂直于地面的方向，且方向向上，并通过质心[8].

1.1.2 整车动力学方程

在建立的整车模型中，为了达到尽量简便和突出研究重点的目的，忽略了叉车复杂的悬架系统，将叉车视为刚体，并且路面为正常行驶的路面.基于以上假设，建立了如图1所示的整车7自由度动力学模型，其中包含横向运动，纵向运动，绕Z轴运动以及4个车轮的旋转.由力学公式得到以下方程.

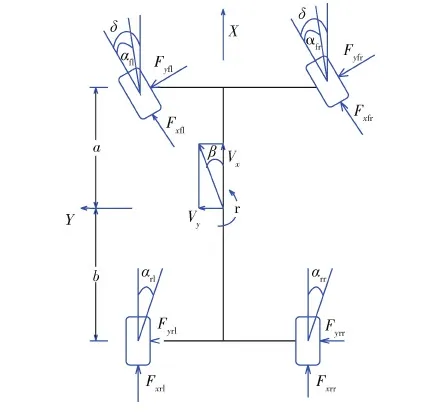
图1 七自由度车辆动力学模型

纵向力平衡方程：

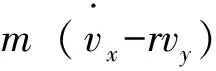
(1)

侧向力平衡方程：

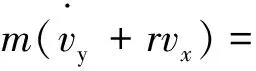
(2)

绕Z轴力矩平衡方程：

(3)

上述方程中：σ为前轮转角；vx、vy分别为纵向、横向车速；β为质心侧偏角；r为横摆角速度；Fxi、Fyi、Fzi分别为轮胎纵向力、侧向力、垂向力；m为整车质量；Iz为整车绕Z轴的转动惯量；a、b为前后轴到质心的距离.

1.2 车轮模型

车轮模型包括车轮动力学模型、轮胎的垂直载荷模型以及侧偏角计算模型.

1.2.1 车轮动力学模型

对叉车行驶时的状态进行受力分析，主要是轮胎与地面的作用力，该作用力直接提供叉车前进的动力.其次是空气阻力对车的影响.4个车轮的力矩平衡方程如下：

(4)

其中，i=左前轮fl、右前轮fr、左后轮rl、右后轮rr.

1.2.2 车轮的垂直载荷

叉车在正常运行情况下，叉车轮胎所承受的垂直载荷在运行期间会不断变化，比如在转向的时候，内侧轮胎所受垂直载荷会变小，而外侧刚好相反.其垂直载荷的计算如下.

各轮胎垂向载荷公式：

(5)

(6)

(7)

(8)

式中：l=a+b为前后轴距；hg为质心到地面的距离；tw1为前轴轮距；tw2为后轴轮距.

1.2.3 车轮的侧偏角

车轮侧偏角指的是车轮的行驶方向与车轮旋转平面之间的夹角，各轮胎侧偏角公式如下.

(9)

(10)

(11)

(12)

1.2.4 滑移率的计算

各车轮轮心在车轮坐标系下的纵向速度：

(13)

(14)

(15)

(16)

式中：vt_fl、vt_fr、vt_rl、vt_rr为轮胎坐标系下的轮胎纵向速度.

各车轮滑移率的计算：

(17)

(18)

(19)

(20)

1.3 电机方程

电机电枢回路电压平衡方程为

(21)

转矩平衡方程：

(22)

其中:

Ed=Ce·n;

(23)

Te=Cm·Id.

(24)

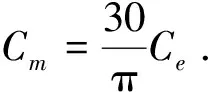
2 H鲁棒控制器设计

γ=min‖P(s)‖.

(25)

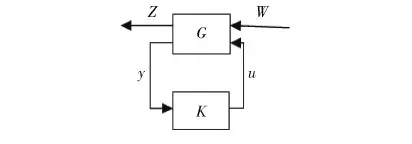
图2 广义反馈系统

在实际控制系统中，外界干扰和叉车本身的不确定性都会影响系统稳定性.对这两者同时进行控制称为H控制的混合灵敏度问题.为了提高系统的性能，要用混合灵敏度来设计控制器，系统框图如下.

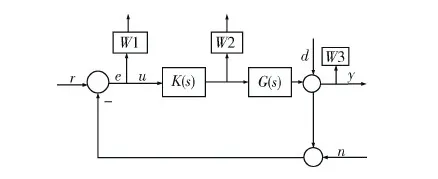
图3 混合灵敏度设计系统

图中：r、e、n、d和y分别表示参考输入、跟踪误差、测量噪声、干扰输入和系统输出；W1、W2，W3分别为系统的为性能权、控制器输出约束权和鲁棒权[10].

设从r到e，u，y，的传递函数分别为

U=(1+GK)-1,

(26)

V=K(1+GK)-1,

(27)

Q=GK(1+GK)-1,

(28)

式中：U是灵敏度函数，而Q是补灵敏度函数.现在我们要选择加权函数W1，W2，W3使之满足：

(29)

加权函数的选择

加权函数的选择至关重要，它的效果好坏会对系统最终的性能有着严重的影响.某种程度上说，对U,V,Q的选择是设计过程中最核心、最关键的一环，且需要满足以下关系[11].

1)灵敏度函数U是闭环系统对干扰抑制的度量，由式(28)得

(30)

2)若加性摄动Δa和乘性摄动Δm满足：

(31)

(32)

3)在低频区有：

U=(1+GK)-1≈(GK)-1,

(33)

V=KU≈G-1.

(34)

4)在高频区有：

U=(1+GK)-1≈I,

(35)

V=KU≈K,

(36)

Q=GKU≈GK.

(37)

以上的几个条件中，4)是最简便的.因此，文中以关系4)为标准来决定加权函数，并用其中的结果对其它指标进行检验.

电子差速系统加权函数的选择

电子差速系统的特性决定了W1具有积分特性或者高增益低通特性，一般取W1(s)=1/(s+1)；W2由系统参数的摄动范围决定，对控制器的输出有很强的制约.在设计系统中，我们在一定范围内选取不同的W2值从而限制控制信号的幅值.为了保持系统阶次的稳定，通常取W2为一常数k2.具体数值应能满足系统的频宽要求，取W2=0.000 05；随后，W3的选取也至关重要.W3一般具有高通性质，取W3(s)=k3s/(s/ω3+1).W3也影响系统频宽，系统频宽与ω3的取值成正比，与k3的取值成反比.为了满足系统的频宽要求，我们取W3(s)=s/(s+1 000).将表1中的参数带入叉车的模型中，得到系统的传递函数. 对被控系统的标称模型进行加权，求解H鲁棒控制器并进行降阶，得到的控制器模型为

(38)

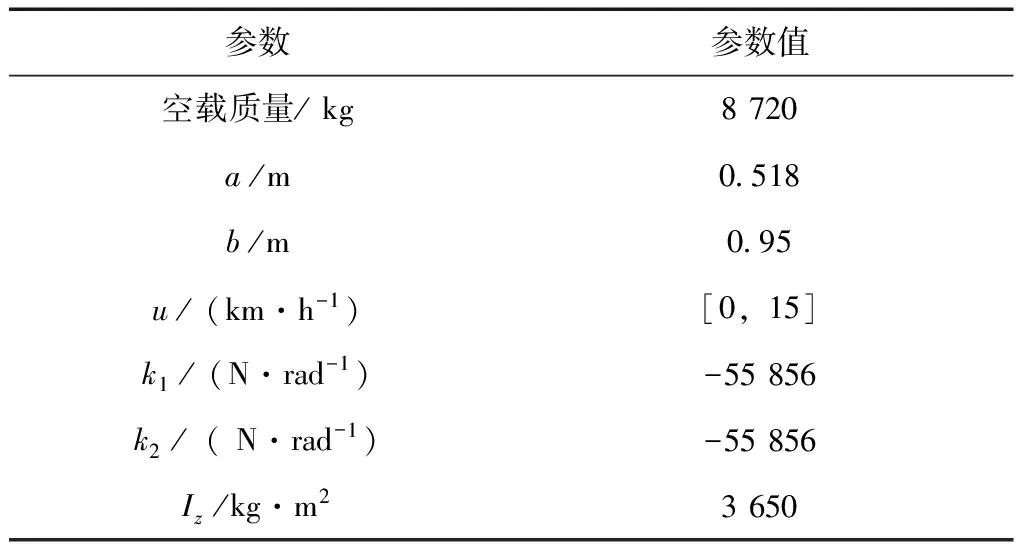
表1 电动叉车参数

3 仿真验证

为了验证所设计控制器的控制效果，在MATLAB2016b平台下进行了仿真验证，将叉车加速到 12 km/h，在8 s时减小转矩输入，在10 s时,给方向盘施加一个 40°角的阶跃输入，在电子差速控制器的作用下，对叉车的行驶状态进行仿真分析.仿真结果结果如图4～9所示.

在没有电子差速控制器的情况下，叉车两侧的轮子输出转矩相等，在仿真过程中，两侧车轮滑移率的仿真结果如图4所示.由图4可知，在转弯的过程中，叉车两侧的滑移率差别很大，说明叉车在转弯的时候没有差速控制来分配各个轮子的转矩，各个轮子都以相同的转矩行进，由于内外轮行驶路径的区别，导致产生的滑移率不同，外轮明显大于后轮.此时，外轮不仅有磨损，还有可能发生滑转，导致叉车行驶不稳定，甚至出现侧翻等严重后果.

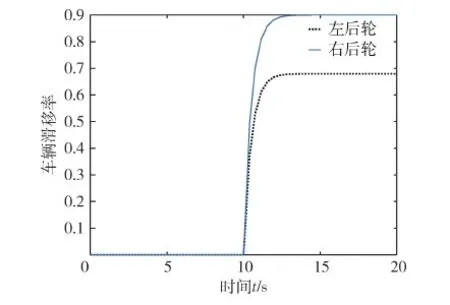
图4 等转矩分配时车轮滑移率

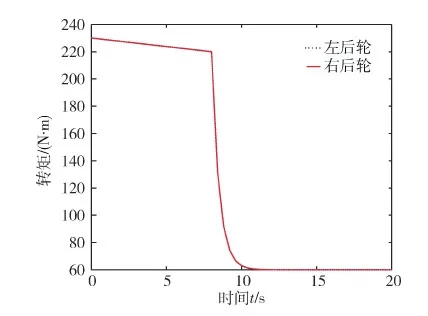
图5 等转矩分配时输出转矩

加入鲁棒控制器之后再进行仿真，得到车轮行驶时的滑移率和转矩变化，如图6和图7所示.由图6可知，加了所设计的鲁棒控制器后，车轮的滑移率稳定在0.2左右，在该范围内，叉车行驶比较稳定，并且前后车轮的偏差接近为0，这对车辆的稳定性至关重要，由图7可知，在前10 s叉车直线加速行驶过程中，两后轮输出的驱动转矩相同；在 10 s 时，叉车开始转弯，与此同时，电子差速器对驱动轮的转矩进行合理分配，在12 s后车轮的转矩趋于稳定.从仿真结果来看，电子差速控制器对于协调转矩，调节叉车转弯时的稳定性有很好的效果.

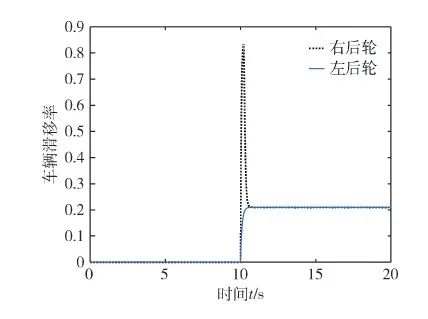
图6 加入鲁棒控制器后的车轮滑移率

在此基础上，继续仿真得到侧向速度与横摆角速度的结果，如图8和图9所示.从仿真结果图来看，叉车在直线行驶的时候，侧向速度和横摆角速度均保持为零；进入转弯过程中，侧向速度与横摆角速度发生突变，且在鲁棒控制下，两者的实际效果更好，经过调节迅速达到稳定的状态；与此同时，左右轮的滑移率的差值一直很小，车轮不会发生明显的滑移.说明叉车转弯时,能达到预期的稳定性，电子差速控制器在转向过程中起到了重要作用.

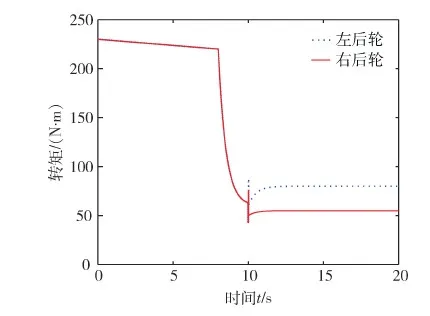
图7 鲁棒控制下的车轮转矩

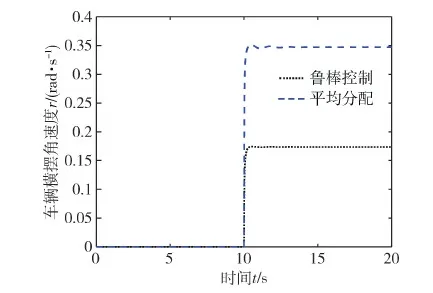
图8 横摆角速度仿真结果

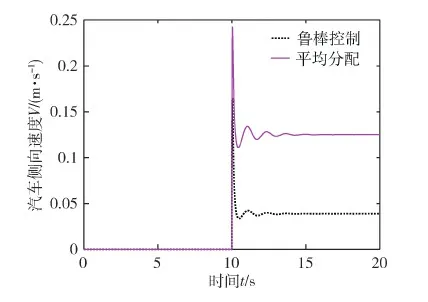
图9 侧向加速度仿真结果

4 结 论

为了提高电动叉车的行驶稳定性，建立了叉车7自由度整车模型，提出了基于H鲁棒控制的电子差速器，仿真结果表明，鲁棒控制器能合理分配转弯时的车轮转矩，使得车轮的滑移率保持一致，从而有效地提高了叉车转向时的稳定性.

参考文献：

[1] 马浩军. 汽车电子差速控制系统研究[D].杭州: 浙江大学, 2016.

[2] Zhao Y, Zhang J. Modelling and simulation of the electronic differential system for an electric vehicle with two-motor-wheel drive [J]. International Journal of vehicle systems Modelling and Testing,2009,4(1):117-131.

[3] Lee J S, Ryoo Y J, Lim Y C,et al. A neural network model of electric differential system for electric vehicle. [C]//Industrial Electronics Society, 2000. IECON 2000. 26th Annual Conference of the IEEE. IEEE, 2000(1): 83-88.

[4] 葛英辉, 李春生, 倪光正. 新的轮毂电机驱动电动车电子差速控制系统研究[J]. 中小型电机, 2003， 30(6): 45-49.

[5] Ravi A, Palani S. Robust electronic differential controller for an electric vehicle[J]. American Journal of Applied Sciences, 2013, 10(11): 1356.

[6] 剧 季，陈淑荣，祝小元.电动汽车混合制动自适应控制研究[J].科学技术与工程，2017，23(7); 96-102.

[7] Lei Xiujun, Zhang Dashan, Jin Yi. Research on vibration suppression of the forklift steering system based on finite element modal analysis and pole placement [J]. Robotics and Manufacturing Automation (ROMA), 2014 IEEE International Symposium on. IEEE, 2015: 46-51.

[8] 张春初. 四轮轮毂电机驱动电动汽车转向工况转矩分配方法研究[D]. 大连：大连理工大学, 2016.

[9] 王 莹. 新型汽车主动悬架系统及其鲁棒控制研究[D]. 广州: 广东工业大学， 2005.

[10] 吴 浩. 轮毂式电动汽车电子差速鲁棒控制研究[D]. 武汉: 武汉科技大学, 2013.

[11] 吴旭东，解学书. 鲁棒控制中的加权函阵选择[J]. 清华大学学报(自然科学版)，1997，37(1): 27-30.