基于LDPC码的联合半盲均衡与解码研究

李 程，黎 勇

(重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065)

0 引 言

随着无线通信技术的高速发展，人们对通信质量的要求也越来越高。不同于有线信道，无线信道中存在各种各样的障碍物，导致接收信号由大量经历了不同传播路径的信号叠加而成，从而会产生严重的符号间干扰(inter-symbol interference，ISI)。

为克服ISI，在接收端一般通过均衡器来校正或补偿系统特性。均衡技术依据是否利用训练序列分为盲均衡方法和半盲均衡方法。盲均衡不需要利用训练序列来对信道进行均衡，大大提高了有效数据的传输效率，主要利用发射信号的先验信息，如统计特征或概率分布和信道的输出序列来对均衡器的参数进行调整，从而达到均衡目的，但盲均衡往往存在相位模糊问题，且复杂度也较高。在实际中应用最多的是半盲均衡方法，通过发送少量的导频符号，从而获得比盲均衡方法更优的性能。

在现代通信系统中，信道编码是实现信息可靠性传输的重要技术之一，它能够在信息传输发生错误后通过一定的规则进行检测和纠正。低密度奇偶校验(low density parity check，LDPC)码是一类具有逼近香农极限的线性纠错码，具有良好的距离特性，较低的译码复杂度，并且可以并行译码,在实际应用中较广泛[1]。

近年来，基于优化理论的线性规划方法成为通信领域的研究热点，文献[2-8]基于线性规划方法对通信技术的基本问题进行了研究，并取得了一系列成果。ZhiDing等[2]提出了一种快速盲均衡算法，以较短的均衡器长度即可实现快速收敛，该算法的提出为均衡技术提供了新的设计思路，为后续的优化算法奠定了理论基础。2005年，J. Feldman等[3-4]利用线性规划松弛，对LDPC码的最大似然(maximum likelihood，ML)译码进行近似求解，提出了线性规划(linear programming，LP)译码算法。与原始译码算法相比，LP译码算法实现将GF(2)上的校验方程转换为实数域的约束条件，极大提高了平均译码效率。LP译码的诸多优点促使人们对其做更多的研究，许多改进的自适应线性规划(adaptive linear programming，ALP)译码算法[5-6]相继被提出。

由于无线信道的信道衰落和噪声的存在，使得信息传输过程变得不可靠。为保证信息尽可能正确传输，逐步提出了将信道均衡和译码相结合的联合均衡与译码技术。如何选用合适的均衡技术，并将信道均衡与译码技术有机结合，对提高系统的整体性能有着重要的影响。文献[7-8]中提出了基于线性规划的联合半盲均衡与译码技术，只需依赖少量的导频符号，便能极大提高均衡的性能。在本文中，将在不损失系统性能的前提下，进一步减少其复杂度。

1 基于线性规划的半盲均衡算法

本文主要研究了ISI信道下的均衡技术，系统模型如图1所示。二进制信息序列f经过LDPC编码器得到码字c，调制器将编码器输出映射到信号星座图对应序列s。调制符号s添加导频p后经过ISI信道传输。发送信号x受到加性高斯白噪声w的影响，接收信号y首先由均衡器进行处理，然后译码器对均衡器的输出序列z进行译码，最终在接收端恢复出原发送二进制信息序列。为了加强理论分析，定义发送信号中导频和数据符号的长度分别为Lp和Ld，对应下标集合为Ip和Id。

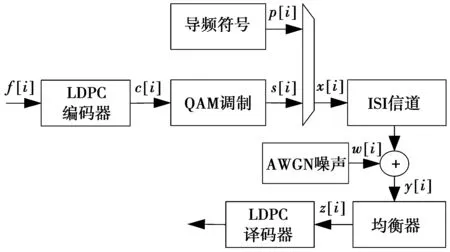
图1 通信模型Fig.1 Communication system model

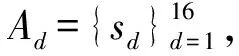
(1)

ISI信道的输入信号x[i]与输出信号y[i]的关系可表示为

(2)

(2)式中,h[k]是信道冲击响应，信道的长度为u+1。由于信道的非理想特性，在接收端会产生严重的码间串扰。

线性均衡器是由一个线性横向滤波器构成，作用于接收信号，目的是将信道与均衡器的整体系统等效成一个单位冲击响应系统，从而消除码间串扰。定义均衡器抽头系数构成的向量为

θ=[θ-Le…θ0…θLe]

(3)

(3)式中，2Le+1为均衡器长度。那么均衡器输出序列表示为

(4)

在理想的条件下，即信道不存在噪声，若均衡器能够完全分离出输入信号，则信道与均衡器必须满足

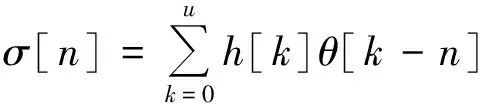
(5)

将线性规划的研究成果引入到通信系统中，为均衡技术的发展提供了新的思路。文献[7]提出了基于线性规划的联合半盲均衡与译码算法，其原理是构造一个凸代价函数，在均衡器参数的线性约束条件下，通过对均衡器系数寻优从而达到最佳均衡的目的。接下来主要分析该均衡器线性规划的数学模型。

1.1 导频符号的约束条件

均衡器的目的就是保证发送信号和均衡器输出序列之间最佳匹配。利用发射端和接收端都已知的训练序列，使用l1准则让线性滤波器的输出导频信号和发送的导频信号之间的误差最小。于是针对导频符号的线性不等式约束为

(6)

1.2 数据符号的约束条件

在实际的数字调制系统中，调制符号是属于一个有限字符集，这一特性已被现有的优化算法利用来恢复发送序列。文献[2]提出了一种基于全局收敛凸函数的盲均衡算法，其物理意义在于使均衡器输出数据序列的实部与虚部绝对值之和最小，具体证明过程详见文献[2]。于是针对数据符号的线性不等式约束为

(7)

1.3 LDPC码的码字约束条件

当受到噪声影响时，均衡器输出符号距离星座图中的点足够近，其欧式距离最小的译码结果存在不满足LDPC码字约束的情况。因此，文献[7]引入了文献[5]提出ALP译码算法。该译码算法通过迭代地添加不被满足的奇偶校验不等式，以较少的有效约束就能达到与原LP译码算法[3-4]相同的性能，具体的算法流程和原理详见文献[5]。调制符号与码字比特流对应的线性关系式见(1)式，通过引入松弛的LDPC码字不等式约束[5]，则针对高阶QAM调制下的联合检测与译码引入的码字约束不等式为

(8)

(8)式中：Nr是LDPC码校验矩阵第r行为1的列下标集合，F⊂Nr,且|F|是奇数。综上所述，得到均衡器LP模型为

(9)

为了方便讨论，定义该算法为联合半盲均衡与译码(joint semi-blind equalization and decoding algorithm，JSBED)算法。设码长为L，均衡器的系数引入的变量数目为4Le+2；由导频符号的不等式约束(6)引入的变量数目为2Lp；数据符号的不等式约束(7)引入的变量数目为2；码字约束不等式(8)引入的变量数目是L+2Ld+16Ld。综上，该线性方程具有2Lp+2Ld+L+16Ld+4Le+4个变量。在该LP模型中，每一个导频与数据符号对应产生4个约束不等式，由于在该方案中自适应添加码字约束，则不计入自适应添加的约束不等式(见(8)式中第4个不等式)的条件下，至少有4Lp+4Ld+9Ld+2L个约束不等式。

为提升系统整体性能，在均衡器输出端再进行一次基于和积算法(sum product algorithm，SPA )迭代译码处理。SPA基于LDPC码字比特之间的奇偶校验关系，利用置信传播迭代计算码字比特错误的概率，迭代更新因子图中的每个节点的概率信息。SPA译码算法需利用均衡器输出符号的对数似然比，其计算式为

(10)

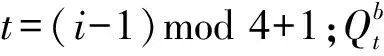
2 简化的半盲均衡算法

通过对算法JSBED的分析，自适应添加的码字约束由于引入了大量的辅助变量，极大地增加了约束方程与未知变量的数量。受文献[7]的启发，本节将对其代价函数与约束条件进行优化。由于JSBED先要对均衡器的输出序列映射到对应比特流，再通过码字约束不等式检验比特流的合法性。为简化该过程，我们尝试去除译码约束得到新的半盲均衡算法，其LP数学模型为

(11)

定义优化后的均衡算法为新半盲均衡(new semi-blind equalization，NSEB)算法。由于该算法仅包含导频与数据符号的不等式约束，则优化算法包含的总未知变量数量为2Lp+4Le+4，约束不等式的数量仅为4(Lp+Ld)。新的代价函数在导频符号与数据符号的不等式约束下，将具有较少的未知变量和约束方程，明显降低了均衡复杂度，且均衡性能得到极大改善。仿真实验对比2种算法的结果将验证该方法的有效性。

优化算法NSEB相对于现有算法JSBED，仅仅去除了LDPC码的LP译码约束，但是其均衡性能并未损失，接下来主要分析造成这种现象的原因。对于高阶QAM调制，需引入辅助变量将码字比特线性映射到信号星座图上。JSBED为了引入码字约束，须将均衡器输出序列映射为二进制比特流，故线性规划方程添加调制映射关系式(1)。那么该算法既可以直接根据最小欧式距离准则对均衡器输出序列进行硬判决译码，又可以根据辅助变量与码字比特的对应关系译码。若算法JSBED设计的合理，以上2种译码方式结果应该保持一致，即星座图上距离均衡器输出z最近的星座点与概率取值最大的星座点(对应于均衡器输出的辅助变量)相同。实验结果表明，这2种译码方式会出现结果不一致的现象。例如：均衡器输出为(-0.948 683,-0.464 375)，对应辅助变量为 (0.744 747, 0, 0.255 253, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0)。很明显，星座图中与均衡器的输出z欧式距离最近的星座点为(-0.948 7,-0.316 2)(此为归一化的星座点)，而星座图中输出概率最大的星座点为(-0.948 7,-0.948 7)，前者译码结果为0001，后者译码结果为0000。

在JSBED算法中，线性调制关系式(1)引入了大量的未知变量，远远超过了约束方程的个数。由于噪声的干扰，均衡器输出并非匹配星座图中各点，那么在解调时满足约束方程的解有多组，而对应的调制关系是一一对应的，这种不匹配会导致码字约束出现误码。自适应添加不被满足的约束条件不仅仅只对码字比特进行奇偶校验，同时也对均衡器的抽头系数进行约束，使代价函数最小的解是两者约束的协调，进一步导致误码率增加。若添加的码字约束能使均衡与译码相互约束和调整，还需研究新的高阶线性调制关系式及LP译码算法。

3 仿真结果与结论

3.1 仿真参数说明与结果

对比分析以上2种算法的性能，仿真参数说明如下：仿真以码率为1/2，码长分别为256和512比特的规则LDPC码，信道的冲击响应为(0.812 4,0.000),(0.406 2,-0.243 7),(0.130,-0.243 7),(-0.008 1,0.160 9),(-0.052 3,-0.078),(-0.049 6,-0.023 3),(-0.031 8,0.003 2),(-0.014 9,0.011 1),(-0.004 1,0.010),(0.001,0.006 3),(0.002 4,0.002 8),(0.002,0.000 7),(0.001 2,-0.000 3),(0.000 5,-0.000 5),(0.000 1,-0.000 4),(-0.000 1,-0.000 2),(-0.000 1,-0.000 1),(-0.000 1,-0.0)导频的长度Lp=8，均衡器长度2Le+1=5。

为有效观察本文讨论的算法的性能，作出误码率随信噪比变化的曲线，如图2所示，其复杂度分析如表1所示。其中，将JSBED算法与SPA算法结合，仿真结果定义为JSBED+SPA；将NSEB算法与SPA算法结合，仿真结果定义为NSEB+SPA。

图2 码长分别为256，512码率1/2，NSEB与JSBED算法的BER曲线Fig.2 BER performance of the NSEB and JSBED algorithms for the length 256 and 512，rate1/2

表1 算法NSEB+SPA与算法JSBED+SPA复杂度分析Tab.1 Complexity of the NSEB+SPA and JSBED+SPA

3.2 仿真结果分析与结论

由图2可知，当码长为256时，优化算法的性能在小范围内略有改善；而当码长为512时，信噪比在9～16 dB时，NSEB相对JSBED有3 dB以上增益，且前者在信噪比为16 dB时，误比特率已达到10-5，而后者仅为10-3。根据表1提供的数据表明，在相同码长的条件下，使用同样数目的导频，优化算法NSEB与JSBED算法相比，极大地减少了LP均衡算法的条件变量和约束不等式的数目，降低了运算的复杂度。

针对文献[7]中提出的联合半盲均衡与译码算法，本文在分析其不足的基础上提出了一种改进算法，在改善性能的同时，减少了约束方程和未知变量的数量，从而极大地降低了联合半盲均衡与译码算法的复杂度。这一算法思想还可以推广到LDPC编码的系统中。

参考文献：

[1] 余格非,王振华,李颖,等.信道编码在无人机数据链中的应用研究[J].重庆邮电大学学报: 自然科学版, 2014, 26(6):845-849.

YU Gefei, WANG Zhenhua,LI Ying, et al. Channel coding in the data link of unmanned aerial vehicle[J]. Journal of Chongqing University of Posts and Telecommunications: Natural Science Edition, 2014,26(6):845-849.

[2] DING Z, LUO Z Q. A fast linear programming algorithm for blind equalization[J].IEEE Transactions on communications, 2000, 48(9):1432-1436.

[3] FELDMAN J, WAINWRIGHT M J, KARGER D R. Using linear programming to Decode Binary linear codes[J].Information Theory IEEE Transactions on, 2005, 51(3):954-972.

[4] FELDMAN J. Decoding error-correcting codes via linear programming[D]. Massachusetts: Massachusetts Institute of Technology, 2003.

[5] TAGHAVI M H N, SIEGEL P H. Adaptive Methods for Linear Programming Decoding[J]. IEEE Transactions on Information Theory, 2008, 54(12):5396-5410.

[6] SARIDUMAN A, PUSANE A E, TAKIN Z C. A heuristic method for adaptive linear programming decoding[C]//IEEE. Signal Processing and Communication Application Conference. Zonguldak, Turkey:IEEE press, 2016:1665-1668.

[7] JACKLIN N, DING Z, LI Y. On efficient use of pilot symbols for multi-path channel equalization of QAM signals[C]//IEEE International Conference on communications. Budapest, Hungary: IEEE press, 2013: 5553-5558.

[8] JACKLIN N, DING Z. On Efficient Utilization of Training Pilots for Linear Equalization of QAM Transmissions[J]. IEEE Transactions on Communications, 2013, 61(61):4984-4996.