空间调制信号的QRD-M检测算法及其改进

周 围，樊 鹏，曾 雪，李 宁

(1.重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065； 2.重庆邮电大学 光电工程学院，重庆 400065)

0 引 言

在4G/5G通信时代，高速可靠的海量数据传输和高频谱效率的需求成为无线通信系统研究的主要任务。多输入多输出(multiple input multiple output,MIMO)天线技术通过分别在发收端配置多根天线传送和接收数据，在不增加系统发射功率和带宽的情况下成倍提升系统信道容量，被认为是现代无线通信关键技术之一[1]。不过，MIMO技术仍然存在一些不足，如信道间干扰(inter-channel interference,ICI)、天线间同步(inter-antenna synchronization,IAS)以及多个射频(radio frequency,RF)链路带来的高成本和高复杂度等问题[2]，制约了MIMO技术的实际运用和部署。

基于此，有文献在2006年提出了一种名为空间调制(spatial modulation,SM)技术的新的多天线传输方案[3]。该技术在每一发送时隙只激活一根天线用来发送数据，一部分输入的信息比特通过激活天线位置所对应的空间维度进行调制，其余比特被调制成激活天线上传输的传统幅度相位调制(amplitude phase modulation,APM)符号。SM技术利用天线的激活位置状态作为一部分传输信息的载体，有效避免了传统MIMO技术中ICI，IAS以及RF代价等问题，具有很好的应用前景。

SM技术的特点使得其接收端的解调有别于传统MIMO技术的信号检测，其系统解调发送信息比特将包括对天线序号和发送符号2个部分的检测信息。在已有的SM信号检测算法中，最优的检测算法是最大似然(maximum likelihood,ML)检测，但其遍历搜索激活天线索引和数字调制符号所有组合的策略，导致该算法有非常高的复杂度，难以用于实际方案[4]。因此，人们相继提出了许多复杂度较低的次最优检测算法，包括最大比合并(maximum ratio combining,MRC)检测算法[5]，球形译码(sphere decoding,SD)检测算法[6]，匹配滤波(matched filters,MF)检测算法[7]，基于信号矢量检测(signal vector based detection,SVD)算法[8]以及基于距离排序检测(distance-based ordered detection,DOD)算法[9]等。文献[10]提出了一种基于M算法的SM检测算法，实现了M算法在SM检测中的应用。

QRD-M(QR-decomposition with M-algorithm,QRD-M)算法是一种结合QR分解的M算法，该算法利用M算法树结构搜索的思想，能够达到性能近似最优且有利于硬件实现，获得了广泛关注[11]。已有文献采用QRD-M算法作为传统MIMO系统的信号检测方案，该方案将ML检测转化为一棵倒置的具有Nt+1层的树搜索过程，将从根节点到叶子节点最短加权路径对应的发送符号作为检测结果，其中，Nt为发射天线数，各层节点对应调制星座点[12]。

与传统MIMO系统中QRD-M算法只检测发送符号不同，SM检测还包括对天线序号的检测，即在树搜索过程中，最短路径将受到发送天线数和调制阶数的共同影响。本文尝试做一些这方面的研究，将QRD-M算法运用到SM检测中，对树的结构做出相应调整，提出基于QRD-M算法的SM信号检测算法，并针对传统QRD-M算法性能受发收天线数影响的缺点，结合并行检测的思想，提出一种新的并行QRD-M(parallel QRD-M,PQRD-M)检测算法，该算法能缩短检测时间，提高算法的执行效率。

1 系统模型

相比传统的二维APM技术，SM技术利用发送天线位置传输信息，从而拓展空间维度，构成新型三维星座调制图。图1为一个发收天线数分别为Nt，Nr的SM系统模型，数字调制(如相移键控(phase-shift keying,PSK)调制，正交振幅调制(quadrature amplitude modulation,QAM)等)的阶数表示为L。SM映射方案将发送比特b一部分用来确定激活天线位置j，j∈Ψ，其余比特映射为传统APM星座点xl，xl∈Ω，其中，Ψ，Ω分别表示激活天线序号集合和数字调制星座点集合。随后，激活第j根发射天线发送相应的APM符号xl。

由于每一发送时隙只激活一根发送天线用于数据传输，此时天线位置可携带的比特数目为lbNt，而传统APM可携带的比特数目为lbL。因此，每一发送时隙中，一个SM发送信号向量共计可携带的比特数目为C=lbNt+lbL。

设x∈CNt×1是只有一个非零元素的发送信号向量，通过SM映射方案后的发送信号向量可表示为[13]

x=[0,0,…,xl,j,0,…,0]T

(1)

(1)式中，xl,j表示被激活天线j上发送的第l个APM星座点。

假设信道为准静态平坦瑞利衰落信道，因此，接收信号可表达为[13]

y=Hx+n=hjxl,j+n

(2)

(2)式中：y=[y1,y2,…,yi,…,yNr]∈CNr×1为接收信号向量；H∈CNr×Nt表示信道矩阵；hij表示信道矩阵的各个元素，各元素之间独立同分布，并服从均值为0、方差为1的复高斯分布；hj表示信道矩阵H的第j列；n∈CNr×1为加性高斯白噪声(additive white Gaussian noise,AWGN)向量，其各元素相互独立，且均服从均值为0、方差为σ2的复高斯分布。

图1 SM系统模型Fig.1 Spatial modulation system model

在接收端已知信道状态信息的情况下，SM系统最优信号检测ML算法可表示为[14]

(3)

由(3)式可以看出，ML最优算法的穷举策略可以得到很好的误码率性能，但其复杂度阶数高达NtL。文献[11]提出了一种应用于传统MIMO系统的QRD-M检测算法，该算法能够降低一定的复杂度，并且达到性能近似最优。本文将结合SM系统的特点，将QRD-M算法应用到SM信号检测中，并针对QRD-M算法的不足，提出基于SM系统的QRD-M检测算法的改进算法。

2 QRD-M检测算法及其改进算法

2.1 基于QRD-M算法的SM检测

QRD-M算法借助QR分解，并将SM检测等价为倒置树结构搜索过程，再设置参数M，以宽度优先的方式对树结构进行搜索，每层保留累积度量值(accumulated metrics,AM)最小的M个分支进行下一层搜索，因而避免了对所有节点进行搜索[15]。

首先对信道矩阵H进行QR分解，即H=QR，其中，Q为Nr×Nt维的正交(酉)阵，R为Nt×Nt维的上三角阵。在(2)式两边同乘以QH，得

(4)

由此，(3)式可以表示为

(5)

(5)式中，rj为上三角阵R的第j列元素。

将(5)式等价为对一个Nr+1层倒置树结构进行搜索，定义第k层(k≤Nr)的节点与其父节点的分支度量值(branch metrics,BM)为

(6)

(6)式中，rkj为上三角阵R的第k行第j列元素。

第k层的累积分支度量为

(7)

图2 QRD-M检测树结构模型(4-QAM，4×4，M=2)Fig.2 Tree structure model of QRD-M detection(4-QAM,4×4,M=2)

2.2 基于改进QRD-M算法的SM检测

传统的QRD-M算法检测过程是在各个分支上按顺序逐个地进行检测，但随着发收天线数增大，树结构的层数和分支数会相应增加，若继续按照传统QRD-M调制方案，一方面算法的执行时间会被延长;另一方面最优解误删的可能性也会增大，如此一来，算法性能将受到影响。

基于此，本文结合并行检测的思想，提出基于QRD-M算法改进的并行检测算法，称为PQRD-M算法。该算法首先将树按备选分支分解成若干个独立的子树，对各子树采用传统的QRD-M算法分别独立地进行搜索，然后将各子树进行联合判决，得到全局累积度量值最小的节点，从而得出检测结果。

PQRD-M算法检测方案叙述如下：当算法搜索到第Nr层时，保留具有最小累积度量值的M个分支，并更新j和xl的集合，其中，xl的集合作为并行检测分支扩展的初始集合。按照j的集合j∈(j1,j2,…,jq)，将树结构分成q个并行的Nr层子树，对每个子树分别进行QRD-M检测，每层保留最小的累积度量值所对应的节点，并更新xl的集合作为下一层扩展的备选集合。然后，在q个子树保留的q个叶子节点中，取累积度量值最小的节点，得出最终的检测结果。

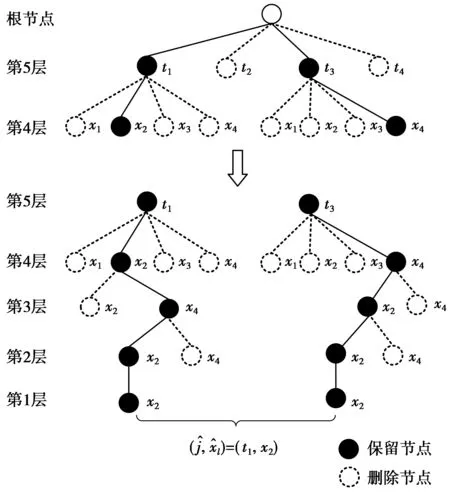
图3 PQRD-M检测树结构模型(4-QAM，4×4，M=2)Fig.3 Tree structure model of PQRD-M detection(4-QAM,4×4,M=2)

3 算法复杂度分析及性能仿真

3.1 算法复杂度分析

文献[16]对算法复杂度的定义为将一个算法中需求值的次数定义为复杂度阶数，将算法中需要进行的实数乘法运算次数定义为计算复杂度。对于一个发收天线为Nt，Nr，调制阶数为L的SM系统，当保留节点数为M时，各算法计算复杂度分析如下，其中，QR分解部分略去。

1)ML检测算法。根据文献[16]，ML检测的复杂度阶数为NtL，计算复杂度为

CML=6NtNrL

(8)

CQRD-M=6NtL+6M2Nr-6M2

(9)

3)PQRD-M检测算法。参照上述对于QRD-M算法的分析， PQRD-M检测的计算复杂度为

CPQRD-M=6NtL+6M2Nr-6M2

(10)

可见PQRD-M算法与QRD-M在实数乘法运算复杂度上一致，不过PQRD-M算法涉及到并行分支和联合判决过程的计算，因此，相较于QRD-M算法，会增加少许计算量。

由此可得，3种算法中，ML检测算法的复杂度最高，QRD-M检测算法的复杂度相比于ML算法大大降低，PQRD-M算法的复杂度相比于QRD-M算法略有增加。

3.2 性能仿真结果

在MATLAB环境下对上述算法进行仿真，并在不同仿真条件下比较各算法的误比特率(bit error ratio,BER)性能。所有仿真过程均假定接收端已知信道信息，并假设信道采用准静态平坦瑞利衰落信道，其各元素满足独立同分布且服从均值为0、方差为1的复高斯分布。

为验证ML，QRD-M，PQRD-M算法之间的性能差异，在发收天线数为4×4，采用4-QAM调制，并取保留节点M的值分别为2和4的情况下进行仿真，结果如图4所示。从图4可以看出，当M取值为4，BER=10-2时，PQRD-M算法和QRD-M算法的信噪比(signal-noise ratio,SNR)值与ML算法的仅分别相差5 dB和8 dB；当M取值为2，BER=10-2时，PQRD-M算法的SNR值优于QRD-M算法3 dB；当M取值为4，BER=10-2时，PQRD-M算法的SNR值优于QRD-M算法4 dB。仿真结果表明，本文提出的QRD-M和改进后的PQRD-M算法均能达到接近于ML最优检测算法的性能，其次，改进的PQRD-M算法性能明显优于QRD-M算法，且M取值越大，改进算法的性能优势越明显。

为验证QRD-M和PQRD-M算法在发收天线数不同时的性能差异，分别在4×4，8×8系统下，采用4-QAM调制进行仿真，其中，M在4×4时取4，8×8时分别取4和8，定义Nt×Nr-QRD-M表示QRD-M算法在Nt×Nr天线数目条件下进行仿真，PQRD-M算法同理，仿真结果如图5所示。从图5可以看出，随着发收天线数的增加，QRD-M算法的性能逐渐下降，在BER=10-3时，8×8-QRD-M(M=4)相比4×4-QRD-M(M=4)性能下降非常明显，8×8-QRD-M(M=8)比4×4-QRD-M(M=4)也依然有大约2 dB性能的下降；而PQRD-M算法很好地改善了这个问题，在BER=10-3时，8×8-PQRD-M(M=4)相比4×4-PQRD-M(M=4)只存在约2 dB性能的下降，8×8-PQRD-M(M=8)相比4×4-PQRD-M(M=4)还存在约3 dB性能的上升。仿真结果表明，改进的PQRD-M算法能够显著改善QRD-M算法性能受发收天线数目影响的缺点，且随着发收天线数的增加，在M取较大值情况下，PQRD-M算法的性能不仅没有受到影响，反而有所提升。

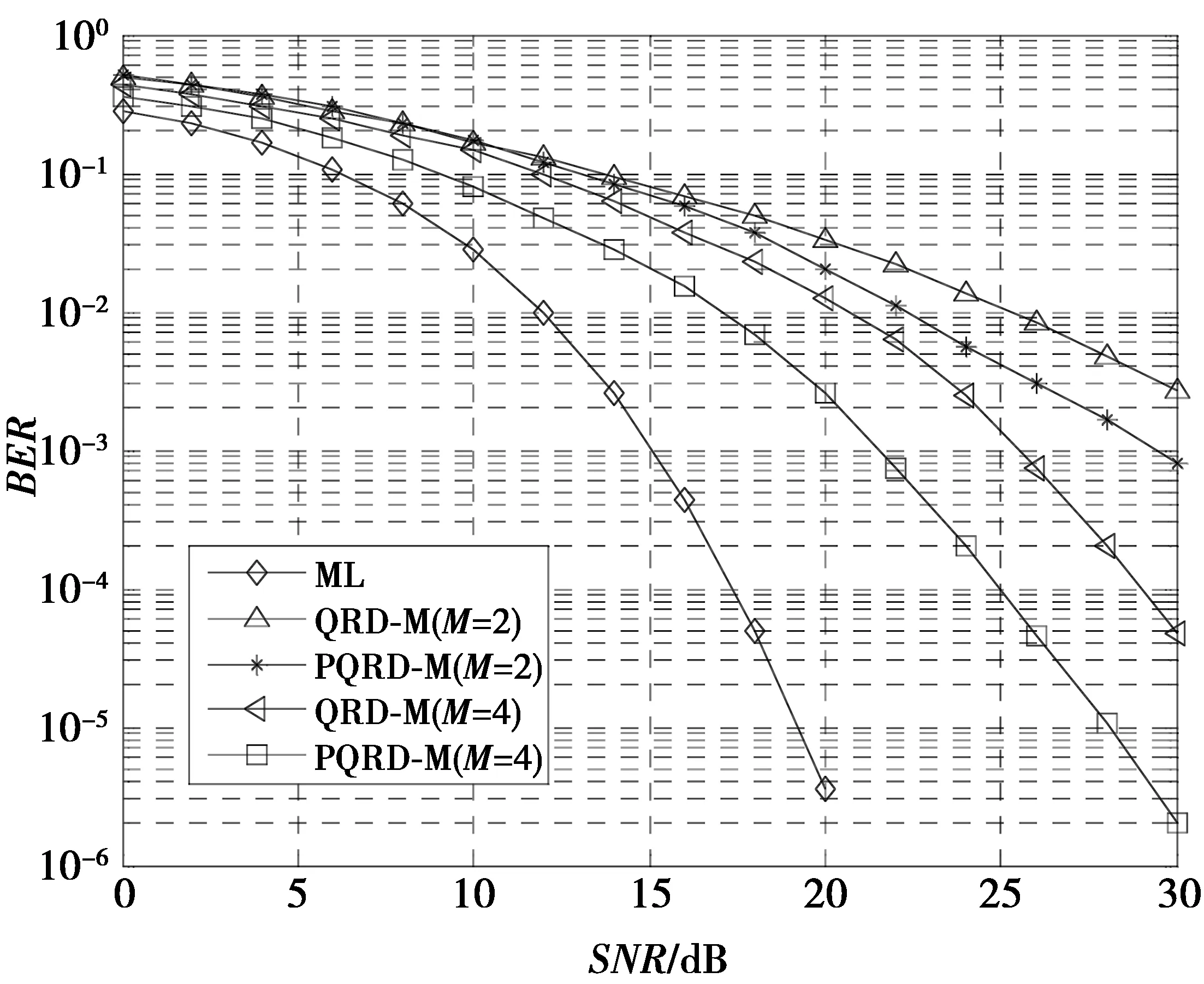
图4 QRD-M及其改进算法与ML算法性能对比Fig.4 Performance comparison among QRD-M, improved QRD-M and ML algorithm

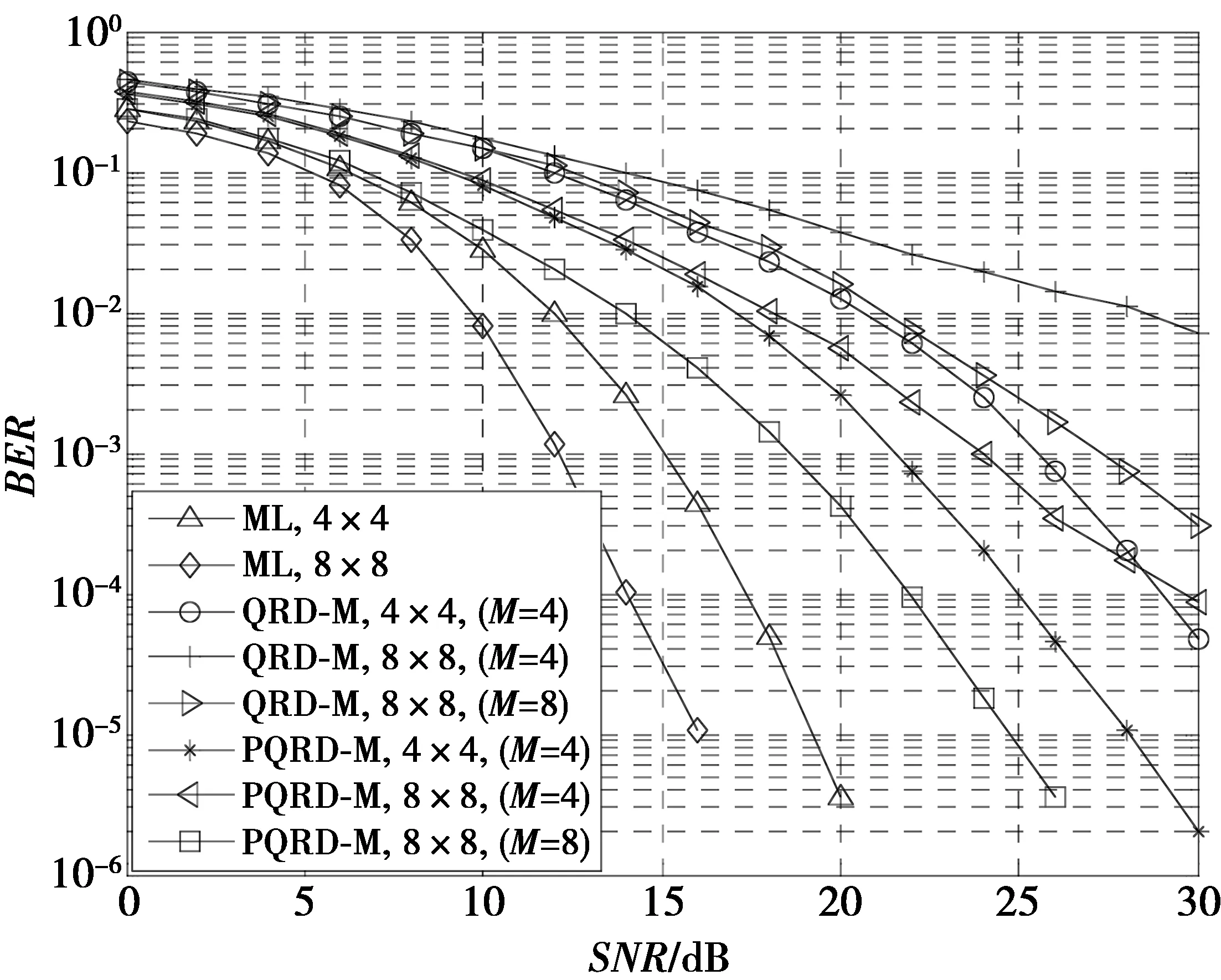
图5 QRD-M和PQRD-M算法性能对比Fig.5 Performance comparison between QRD-M and PQRD-M algorithm

4 总 结

本文针对SM系统最优ML检测算法高复杂度问题，提出了基于SM系统的QRD-M检测算法。该算法借助QR分解和M算法，将信号检测转化为树结构搜索的过程，以宽度优先的方式，对每层保留的具有最小累积度量值的M个分支进行搜索，因而避免了搜索所有节点，在保证性能近似最优的情况下大大降低了计算复杂度。但研究发现，该算法性能会随着发收天线数的增大而降低，并且算法执行时间也会延长。针对该问题，引入并行检测的思想，提出改进的QRD-M算法，即PQRD-M检测算法。该算法将树结构分为M个子树结构，同时进行QRD-M检测，一方面可以有效利用硬件并行处理的优势，缩短算法执行时间；另一方面也降低了最优点误删的可能性，提升了算法性能，缺点是相比于传统QRD-M算法，计算复杂度略有增加。

参考文献：

[1] HU Bibo, LIU Yuan’an, XIE Gang,et al. Energy efficiency of massive MIMO wireless communication systems with antenna selection [J]. The Journal of China Universities of Posts and Telecommunications,2014,21(6):1-8.

[2] GOLDSMITH A, JAFAR S, JINDAL N, et al. Capacity limits of MIMO channels [J]. IEEE Journal on Selected Areas in Communications(JSAC),2003,21(5):684-702.

[3] MESLEH R, HAAS H, AHN C W,et al.Spatial modulation-a new low complexity spectral efficiency enhancing technique[C]//IEEE.ChinaCom' 06 First International Conference on Communications and Networking in China. Beijing: IEEE Press, 2006: 1-5.

[4] RENZO M D, HASS H. Performance analysis of spatial modulation[C]//IEEE CHINACOM Beijing. Beijing: IEEE Press, 2010: 1-7.

[5] MESLEH R,HAAS H,SINANOVIC S,et al.Spatial modulation[J].IEEE Transaction on Vehicular Technology，2008, 57(4): 2228-2241.

[6] YOUNIS A, SINANOVIC S, RENZO D M. Generalised sphere decoding for spatial modulation[J].IEEE Transactions on Communications,2013, 61(7): 2805-2815.

[7] SUGIURA S, XU C, NG X, et al. Reduced complexity coherent versus non-coherent QAM-aided space-time shift keying [J]. IEEE Transactions on Communications, 2011, 59(11): 3090-3101.

[8] WANG J, JIA S, SONG J. Signal vector based detection scheme for spatial modulation [J]. IEEE Communications Letters, 2012, 16(1): 19-21.

[9] TANG Qian,XIAO Yue,YANG Ping,et al.A new low-complexity near-ML detection algorithm for spatial modulation[J].IEEE Wireless Communications Letters, 2013, 2(1): 90-93.

[10] 张新贺,金明录.空间调制信号的改进M-ML检测算法[J].大连理工大学学报, 2016, 56(2): 140-146.

ZHANG Xinhe, JIN Minlu. Improved M-ML algorithms for spatial modulation signal detection[J].Journal of Dalian University of Technology, 2016, 56(2): 140-146.

[11] KIM B, CHOI K. A very low complexity QRD-M algorithm based on limited tree search for MIMO systems [C]//Vehicular Technology Conference. Toronto: IEEE Press，2008: 1246-1250.

[12] 刘丽.MIMO系统信号检测算法研究[D].沈阳:东北大学,2012.

LIU Li. Study on signal detection algorithms for MIMO systems [D]. Shenyang: Northeastern University, 2012.

[13] 门宏志,金明录.低复杂度空间调制MPSK信号的最优检测[J].通信学报,2015,36(8):118-124.

MEN Hongzhi,JIN Minlu.Low-complexity optimal MPSK detection for spatial modulation[J].Journal on Communications, 2015, 36(8): 118-124.

[14] ZHENG Jianhong,YANG Xiaobo,LI Zhe. Low complexity detection method for spatial modulation based on M-algorithm[J].Electronics Letters,2014,50(21): 1552-1554.

[15] JIN KIM K, JIANG YUE, ILTIS R A, et al.A QRD-M/Kalman filter-based detection and channel estimation algorithm for MIMO-OFDM systems[J].IEEE Transactions on Wireless Communications,2005,4(2): 710-721.

[16] MEN Hongzhi,JIN Minlu. A low-complexity ML detection algorithm for spatial modulation systems with MPSK constellation[J].IEEE Communications Letters, 2014, 18(8):1375-1378.