等截面薄壁空心墩宽厚比限值研究*

周水兴，严成俊

(重庆交通大学 土木工程学院，重庆 400074)

0 引 言

随着高速公路、高速铁路的大量修建，出现了诸多空心薄壁桥墩。国内外针对高墩稳定问题已开展大量研究，主要侧重于高墩特征值、极限承载力和施工缺陷对稳定的影响分析[1-4]，围绕空心薄壁墩局部屈曲与板厚关系的研究相对较少。空心墩是由薄板组成的板壳构件，工程设计中除需满足桥墩承载力、整体稳定外，还应考虑薄板的局部稳定问题。彭元诚[5]针对龙潭河大桥178 m空心薄壁墩，推导了不同约束条件下满足混凝土薄壁局部稳定的最小宽厚比。

笔者基于沿中心压杆均匀分布的自重与杆端集中力具有相同稳定系数的条件，推导了考虑自重和杆端集中力共同作用下的中心压杆临界荷载计算公式，在此基础上根据薄壁空心墩优先发生整体失稳破坏的破坏形式，以桥墩整体稳定应力小于壁板临界应力作为控制条件，推导了等截面桥墩受压壁板应满足的临界宽厚比(临界厚度)计算公式，通过算例和有限元分析验证笔者推导公式的正确性。

1 等截面中心压杆临界荷载计算公式

表1为下端固结、上端自由与上端铰接两种边界条件下，等截面中心压杆在均布荷载和杆顶集中荷载单独作用下的临界荷载[6-7]。

表1 不同荷载单独作用时的失稳荷载Table 1 Failure load under different load alone

当均布荷载和集中荷载共同作用时，相应的临界荷载可用贝塞尔函数求解：

(1)

式中：m为杆件自重与欧拉荷载的比值，m=ql/PE；U为对应贝塞尔方程的最小根，查贝塞尔函数表可得。

由于式(1)计算临界荷载较为复杂，笔者将沿杆件长度均匀分布的自重荷载ql等效为一作用在杆件顶端的集中力P1，施加在杆顶的集中力为P2。

记P1=ψql，利用P1与(ql)具有相同的稳定系数，有P1λq=PE，(ql)λq=(ql)cr，则有(ψql)λq=ψ(ql)cr，得ψ=PE/(ql)cr。利用表1临界荷载值，不难得到下端固结上端自由时ψ=0.314，下端固结上端铰接时ψ=0.383。

对于工程中常见的桥墩构造，同时受到P1和P2的共同作用，因此有必要进一步考察其共同作用下的临界荷载。在弹性稳定分析中，稳定系数λ常按λ(P1+P2)计算。

设等效集中力P1和P2同时作用至杆件失稳时，P2的临界荷载为Pcr，杆件失稳时，有

(P1+P2)λ=PE

令P2=φql，则上式可表示为

(2)

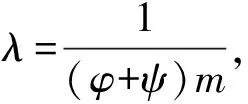
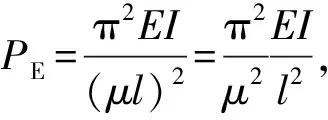
(3)

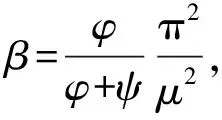
为验证上述算法的正确性，以下端固结上端自由为例进行计算，并采用ANSYS建立有限元模型进行验证。桥墩截面如图1，截面参数为：b=6.5 m，c=3.5 m，t=0.6 m，tc=0.6 m，桥墩高度l取为55 m进行验算。桥墩材料为C40混凝土，其弹性模量为E=3.25×104MPa，泊松比为ν=0.2，质量密度为ρ=2 500 kg/m3。

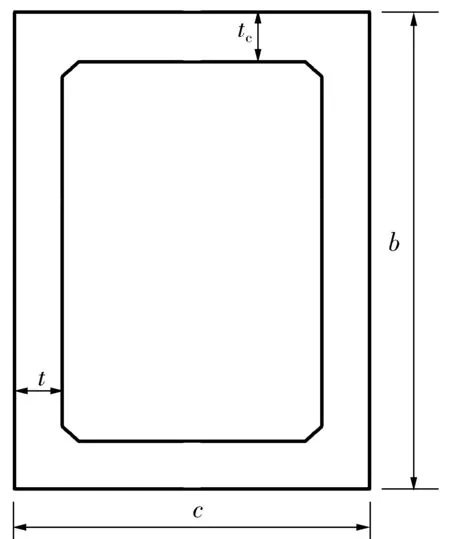
图1 桥墩横截面Fig. 1 Pier cross section

根据桥墩截面参数有

I=[6.5×3.53-(6.2-2×0.6)×(3.5-2×0.6)3]/12=17.85(m4)

A=6.5×3.5-(6.5-2×0.6)×(3.5-2×0.6)=

10.56(m2)

q=2 500×10.56×10=264 000(kN/m)

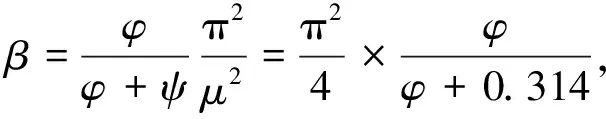
将φ=5、10和l=65、75、85、95代入式(3)计算各墩高下的临界荷载，并与有限元模型对比，结果如表2和表3。根据计算结果的分析可以得出：将自重等效为墩顶集中荷载进行临界荷载的计算是可行的，且公式计算值与有限元分析的结果吻合度较好，误差在工程可接受的范围5%以内。

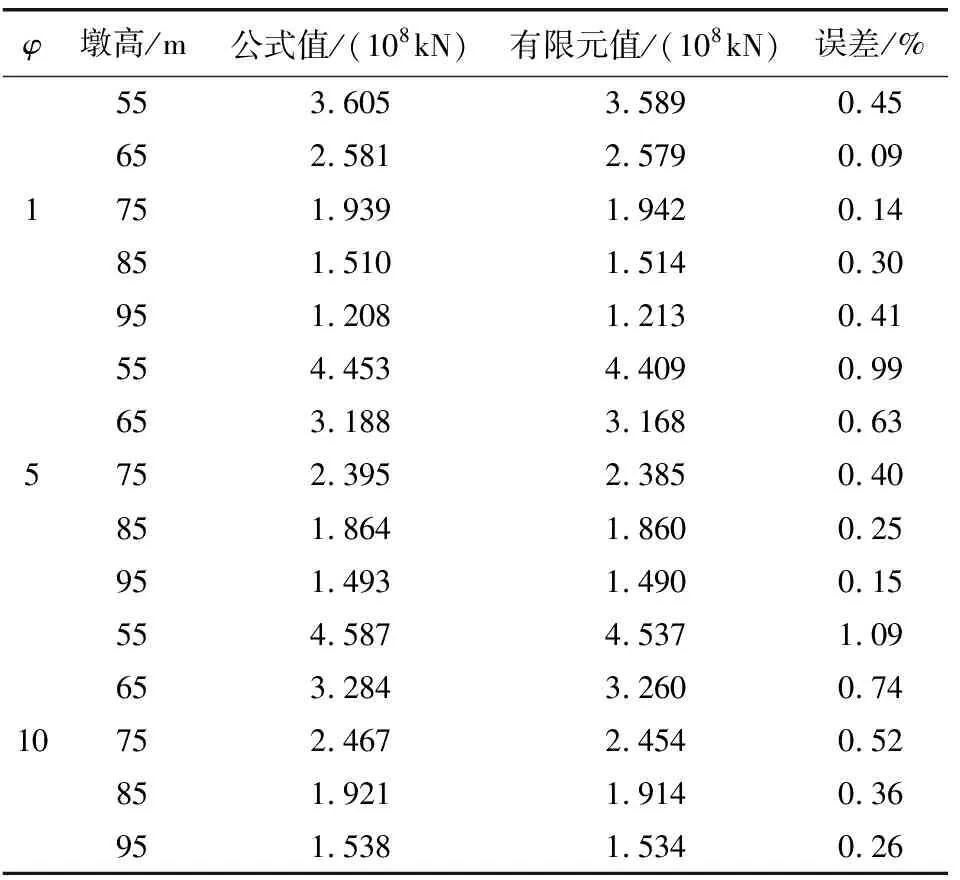
表2 下端固结上端自由临界荷载对比Table 2 Contrast comparison of critical loads with lower end consolidated and upper end free

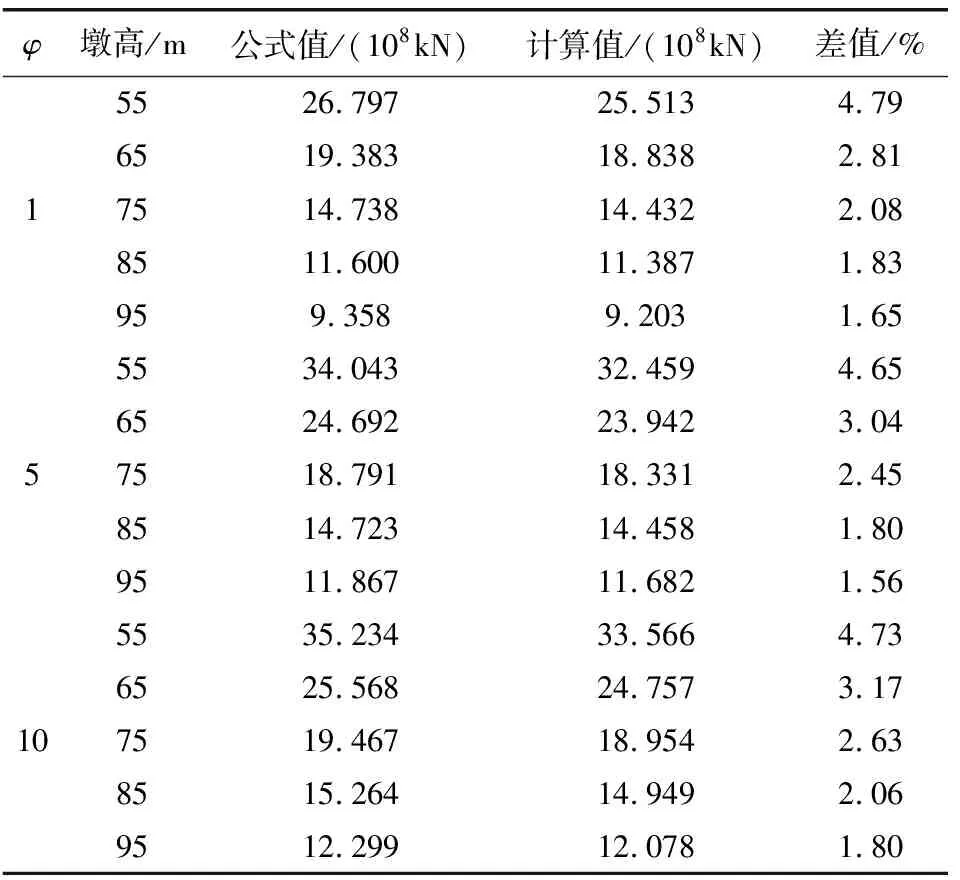
表3 下端固结上端水平约束临界荷载对比Table 3 Contrasting critical load of Lower end consolidation and Upper horizontal constraint

根据临界荷载可得相应的临界应力为

(4)

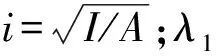
实际工程中，薄壁空心墩多为混凝土结构，在材料进入弹塑性阶段后，需要对公式中的弹性模量进行修正，用切线模量ET代替弹性模量E。令t=ET/E，弹塑性阶段临界应力为

(5)

2 薄壁空心墩极限宽厚比公式

与实体墩相比，薄壁空心墩以较少的材料获得较大的截面抵抗惯性矩，充分发挥材料的力学性能，满足墩柱整体稳定与刚度要求。薄壁空心墩既存在整体稳定问题，又存在壁板局部稳定问题。壁板的局部稳定可以通过限制板的宽厚比，以局部屈曲容许应力高于整体稳定应力来得到保证。

薄壁空心墩壁板的局部稳定可根据弹性薄板受均布压力屈曲得出。纵向压力作用下，薄板离开平面位置而发生屈曲导致局部失稳。仅有一个方向受压薄板屈曲，如图2。

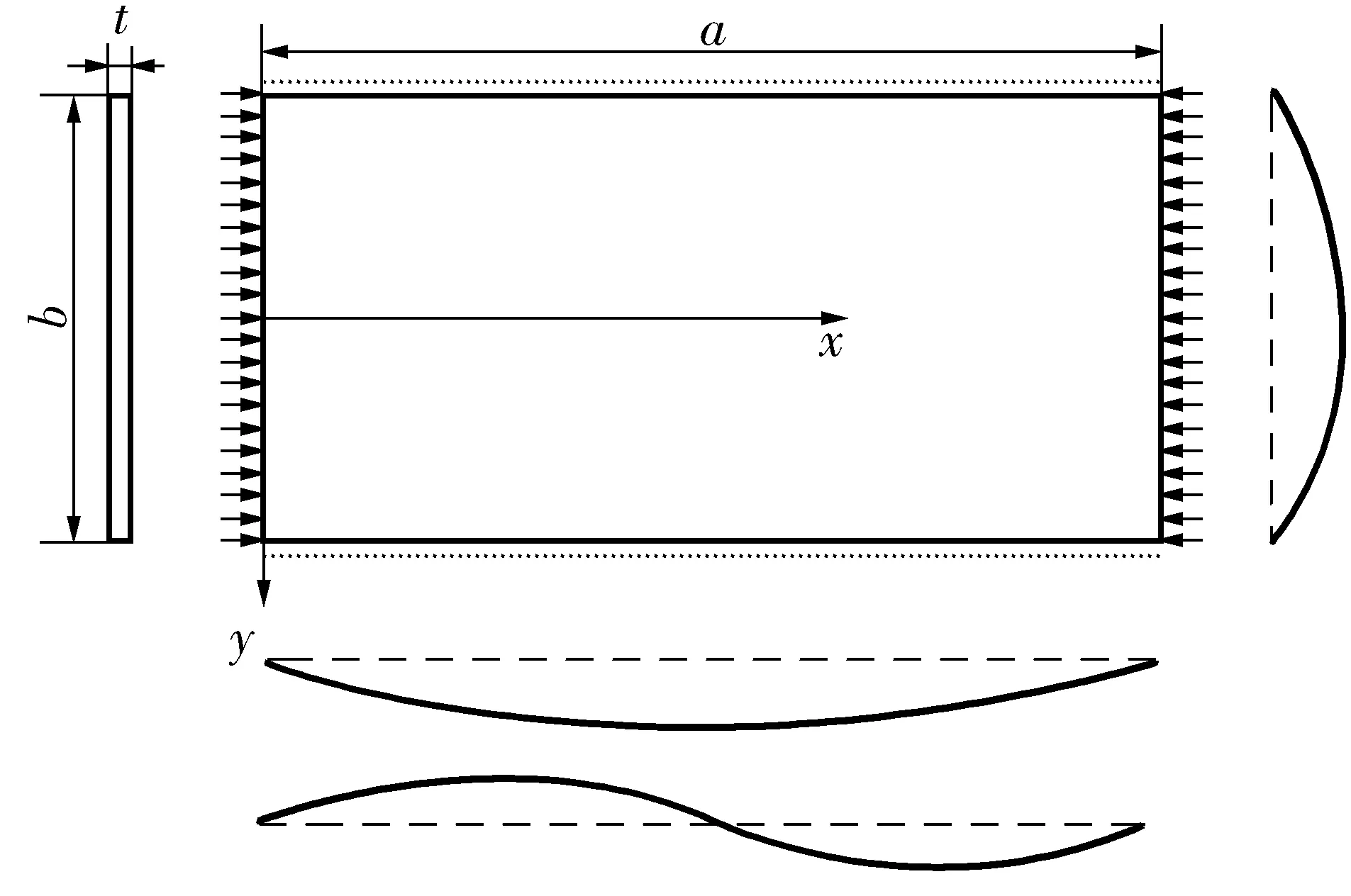
图2 薄板屈曲Fig. 2 Sheet buckling

两端受均布压力作用的薄板弹性翘曲方程为

(6)

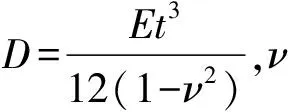
对四边简支的边界条件，板的屈曲挠度可用式(7)的双级数来表示：

(7)

式中：m、n分别为板屈曲时沿x轴和y的半波数，m、n=1，2，3，…。

将挠度曲线代入式(6)，整理后可得到弹性屈曲的临界荷载为

(8)

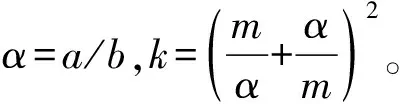
式(8)进一步表示为

(9)

可以证明，k关于自然数域m的最小值为4[8]，由此得

(10)

混凝土薄壁结构一般发生弹塑性失稳，当用桥墩整个截面计算临界应力，并考虑混凝土的弹塑性时，式(10)改写为[9]

(11)

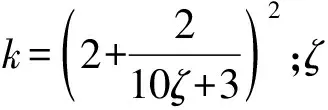
根据薄壁空心墩整体失稳先于局部失稳破坏，即局部应力与整体应力有σc≥σcr的关系：

(12)

由式(12)可得薄壁空心墩受压壁板的极限宽厚比为

(13)

将混凝土材料泊松比ν=0.2、τ=0.5代入式(13)，得宽厚比限值计算公式为

(14)

由式(14)进一步得到薄壁桥墩极限厚度计算式：

(15)

利用式(15)可计算已知板宽时的薄壁空心墩临界厚度。由于板厚的改变会影响到截面回转半径i和构件长细比λ1，因此需要循环迭代来求解壁厚t，相应计算流程见图3。

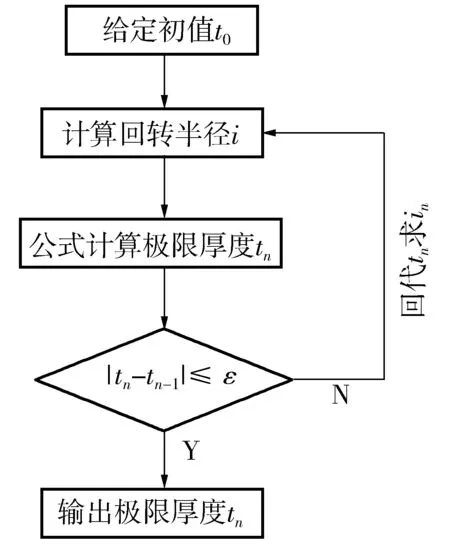
图3 极限厚度求解流程Fig. 3 Limit thickness solving flowchart

3 算例验证

某空心薄壁墩高55 m，C40混凝土，弹性模量E=3.25×104MPa，重力密度为ρ=25 kN/m3。桥墩横截面外形尺寸为6.5 m×3.5 m，顺桥向壁厚tc=0.60 m(确保受压板的荷载主要沿着短边传播，即受压板为单向板)，横桥向壁厚为t，横截面如图4。

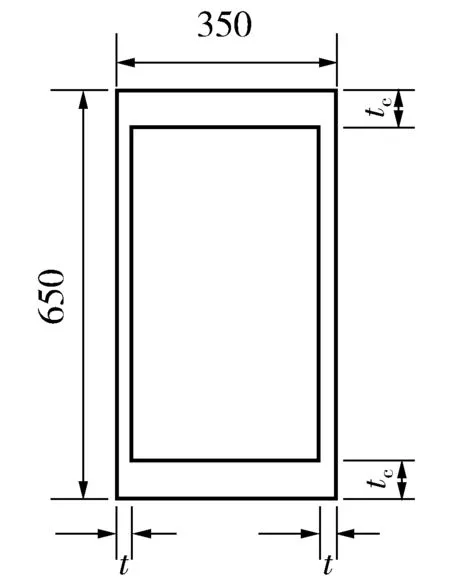
图4 薄壁空心墩截面(单位：cm)Fig. 4 Cross-section of thin-walled hollow pier

以下端固结上端自由为例，计算桥墩仅在自重作用下横桥向壁板的极限厚度t。第1次试算时取t=20 cm，有

A=6.5×3.5-(6.5-2×0.6)(3.5-2×0.2)=

6.32(m2)

I=[6.5×3.53-(6.5-2×0.6)(3.5-2×

0.2)3]/12=10.066(m4)

43.582

将上述参数代入式(15)，得板厚t为

将t=0.131 m作为第2次试算的初值，重复上述计算过程，直到极限厚度t不再发生变化为止，最终得到t=0.124 m。

为分析不同墩高下临界厚度变化规律，分别选取桥墩高度为65、75、85和95 m，计算结果如表4。

为进一步验证文中公式的正确性，利用ANSYS的SHELL63单元建立有限元模型，计算各种墩高下的临界厚度，相应结果如表5。

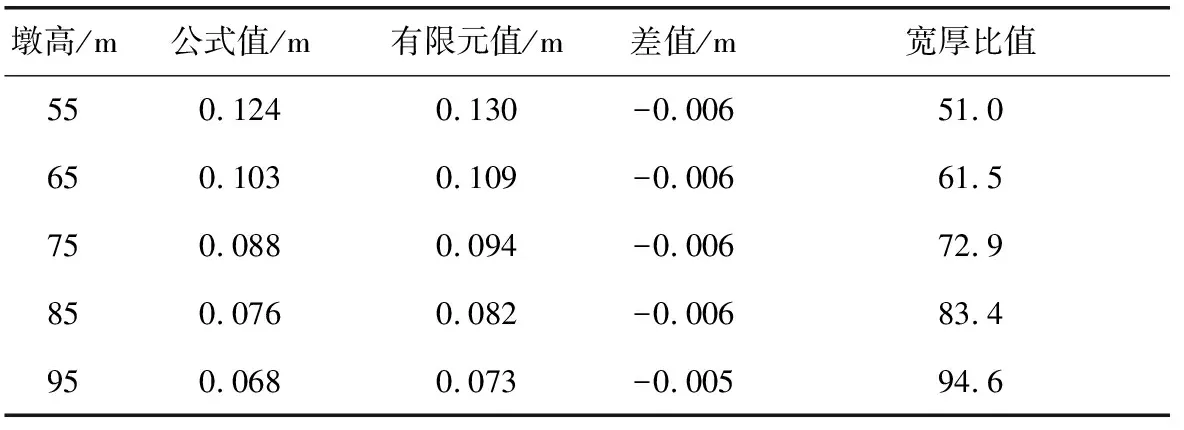
表4 下端固结上端自由在桥墩自重作用下的结果Table 4 Result of pier under pier self-weight with lower end consolidation and top free

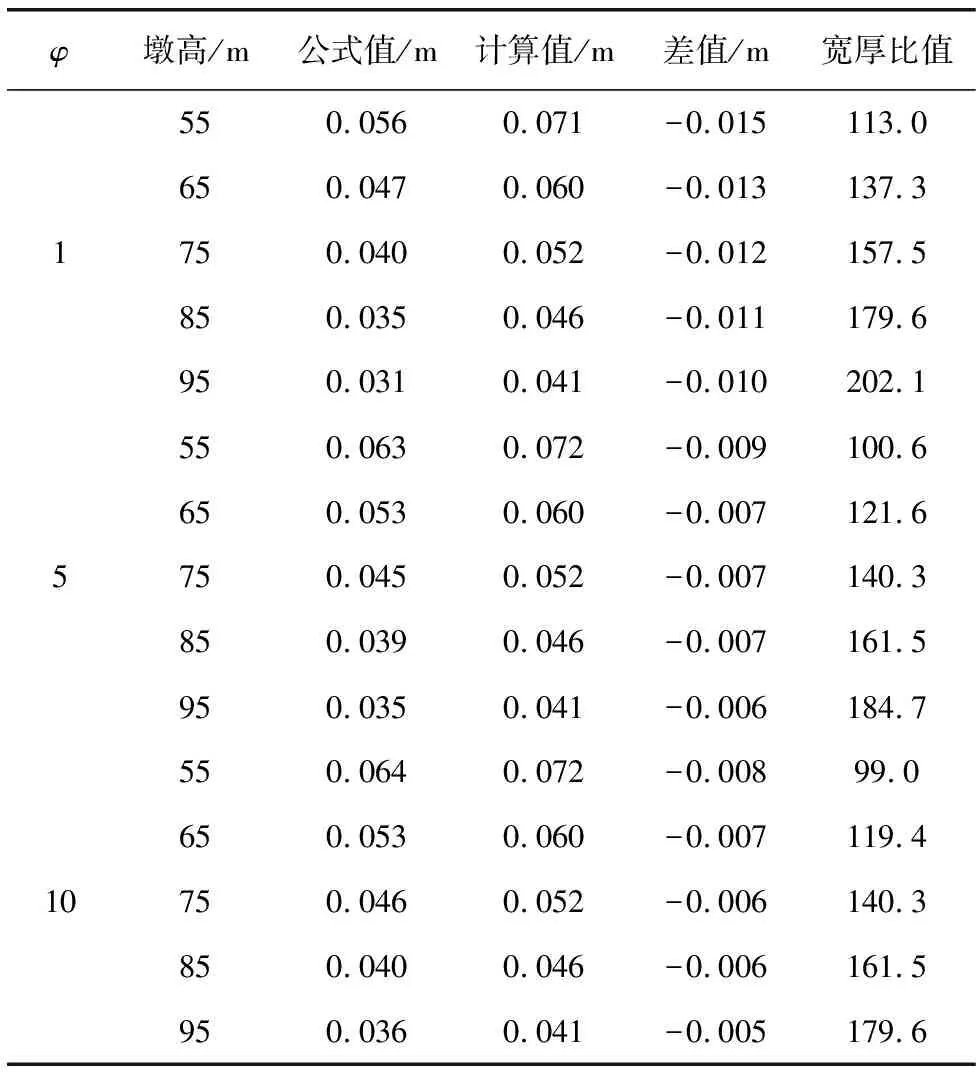
表5 下端固结上端自由的桥墩临界厚度Table 5 Critical thickness of pier with lower end consolidation and top free

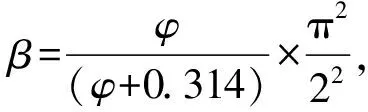
经试算最终得t=0.057 m。同理可计算出下端固结、上端铰接边界条件，由桥墩自重与墩顶集中力共同作用下桥墩临界厚度，如表6。由表6可得：① 随着桥墩高度的增加，极限厚度减小，这可以从临界荷载的计算公式PE=π2EI/(μl)2得到解释，随着桥墩高度的增大临界荷载相应减小，临界应力也随之减小，导致极限厚度也减小，宽厚比限值增大；② 按推导公式得到的计算值均小于有限元结果，是由于公式计算时考虑了混凝土的弹塑性，有限元分析中混凝土为弹性材料；③ 在桥墩自重与集中力共同作用下，随着集中力P2增大，理论计算值与有限元结果间的误差减小，当集中力P2与自重之比达到5倍时，两者误差在1 cm以内，表明集中荷载越大，自重对稳定的影响越小；④ 公式计算结果与有限元结果随着墩高增加而趋于减小。

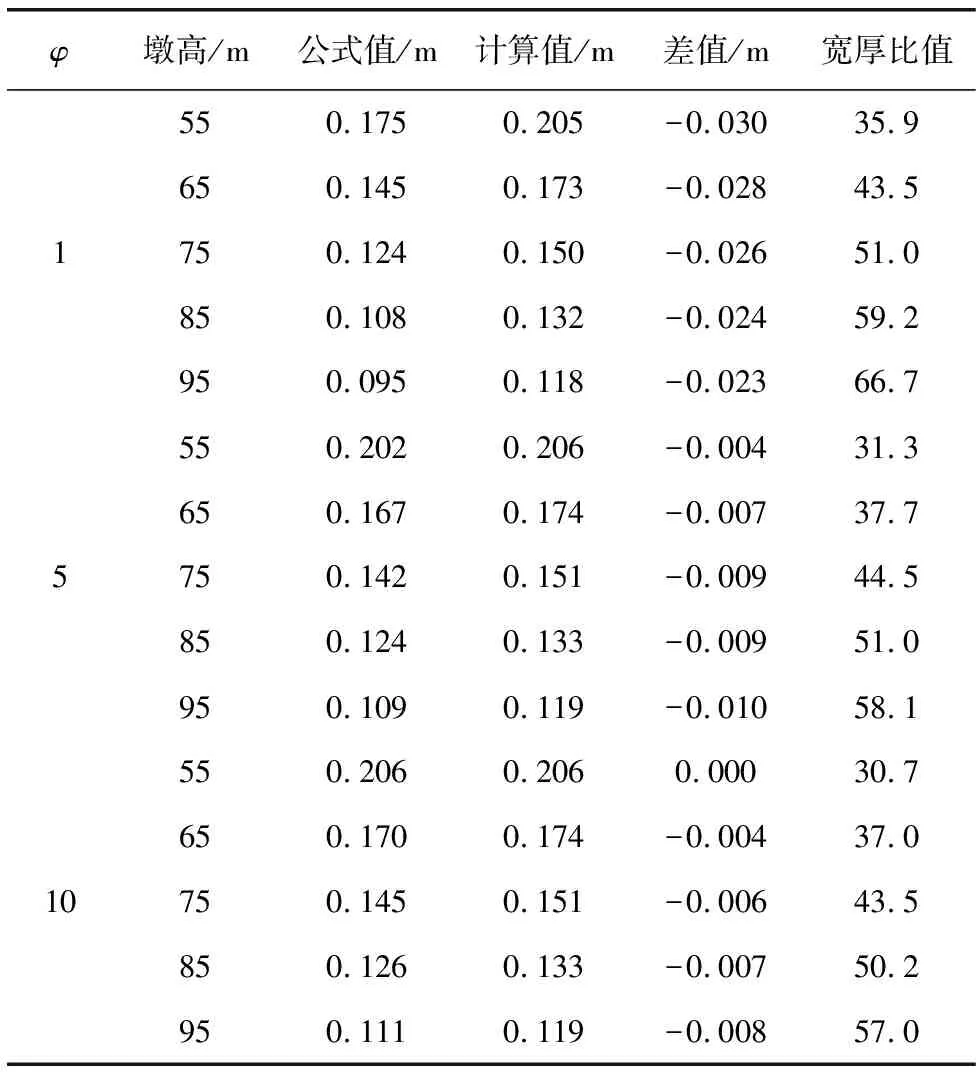
表6 下端固结上端铰接的桥墩临界厚度Table 6 Pier critical thickness of bottom fixed and top hinged

4 结 语

笔者将桥墩自重等效为墩顶集中荷载，推导了自重与集中力共同作用下的临界荷载计算公式。基于桥墩整体稳定应力小于壁板临界应力为控制条件，推导了桥墩受压壁板应满足的临界宽厚比(临界厚度)计算公式，通过算例验证了公式正确性，可为桥墩构造设计提供参考。但笔者未考虑初始缺陷、横向风荷载等对桥墩壁厚的影响，及地震作用的影响，为此，需要开展进一步的研究。

参考文献(References)：

[1] 李开言，陈政清，韩艳.双肢薄壁高墩施工过程稳定性分析的快速算法[J].铁道学报，2004，26(5)：86-90.

LI Kaiyan，CHEN Zhengqing，HAN Yan.Quick arithmetic of analysis of stability of double-leg thin-wall high piers during construction[J].JournaloftheChinaRailwaySociety，2004，26(5)：86-90.

[2] 吕毅刚，余钱华，张建仁.能量法分析高墩大跨连续刚构桥稳定性[J].长沙理工大学学报(自然科学版)，2005，2(4)：22-27.

LV Yigang，YU Qianhua，ZHANG Jianren.Stability analysis of the continuous rigid frame bridge with long-span and high-pier via energy method[J].JournalofChangshaUniversityofScienceandTechnology(NaturalScienceEdition)，2005，2(4)：22-27.

[3] 周水兴，满泽联，周光强，等.连续刚构桥组合式桥墩临界荷载分析[J].重庆交通大学学报(自然科学版)，2014，33(1)：17-20.

ZHOU Shuixin，MAN Zelian，ZHOU Guangqiang, et al.Critical load analysis of continuous rigid frame bridge combined bridge pier[J].JournalofChongqingJiaotongUniversity(NaturalScience)，2014，33(1)：17-20.

[4] 王飞，曹传林，方志.基于能量原理的双肢薄壁高墩稳定计算[J].中外公路，2006，26(1)：96-100.

WANG Fei，CAO Chuanlin，FANG Zhi.Stability calculation of double leg thin walled high pier based on the principle of energy[J].JournalofChina&ForeignHighway，2006，26 (1)：96-100.

[5] 彭元诚.龙潭河特大桥静力稳定性及风致抖振时域分析[D].武汉：华中科技大学，2006：19-24.

PENG Yuancheng.StaticStabilityAnalysisandTimeDomainWind-InducedBuffetingAnalysisofTheLongtanheLong-spanBridge[D].Wuhan：Huazhong University of Science and Technology，2006：19-24.

[6] TIMOSHENKO S P，GERE J M.TheoryofElasticStability[M].2nd ed.New York：McGraw-Hill，1961：107-110.

[7] A.H.金尼克.纵向弯曲与扭转[M].上海：上海科学技术出版社，1964：107-109.

KIM NICK A H.LongitudinalBendingandTorsion[M].Shanghai：Shanghai Scientific & Technical Publishers，1964：107-109

[8] 李国豪.桥梁结构稳定与振动[M].北京：中国铁道出版社，1996：217-219.

LI Guohao.StabilityandVibrationofBridgeStructure[M].Beijing：China Railway Publishing House，1996：217-219.