顺层岩质边坡溃屈型破坏探讨*

张登项，唐 川，唐秋元

(中煤科工集团重庆设计研究院有限公司 岩土工程院，重庆 400042)

0 引 言

顺层岩质边坡是指岩层层面的倾向与边坡坡向一致的边坡，随着人类工程活动的影响，工程开挖而形成的顺层岩质边坡的稳定性问题也越来越突出，这也引起了人们对顺层岩质边坡破坏模式与机制的研究。许多学者通过对大量顺层岩质边坡进行研究，将这类边坡按岩层倾角的大小大致分为两类：缓倾顺层岩质边坡和陡倾顺层岩质边坡[1]。并总结了影响顺层岩质边坡稳定性的相关因素，得出了顺层岩质边坡的破坏模式以及相关的计算力学模型[1-12]。

综合前人研究，可以得出缓倾和陡倾顺层岩质边坡的破坏模式和力学机制各有不同，特别是对于陡倾顺层岩质边坡存在着一种特殊的破坏模式——溃屈型破坏[13]。实际工程运用中，由于运用规范推荐的传统刚体极限平衡分析这类陡倾顺层岩质边坡得到的稳定性结果都比较好[14]，故这种潜在的特殊破坏模式往往被人们所忽略。

笔者首先对岩质边坡溃屈型破坏的力学原理进行探讨，然后结合一典型陡倾顺层岩质开挖边坡实例，运用离散元法模拟非连续介质独特的优势[15]，得出岩质边坡发生此破坏模式的变形、应力特征以及具体破坏过程。

1 力学原理

岩质边坡发生溃屈型破坏力学模型如图1[13]。

图1 溃屈型破坏力学模型Fig. 1 Mechanical model of yield failure

设坡面AD与层面BC完全平行，那么能够使斜坡保持稳定的最大边坡高度Hmax，可按照如下步骤计算：首先假设一个潜在破坏体ABCD的庞大自重使其坡脚的岩体处于塑性状态，该塑性区域近似用直角三角形ABE表示，塑性区上部的岩体EBCD仍处于弹性状态，并假定其自重为G。

潜在破坏体ABCD自重G：

(1)

陡倾结构面BC上的抗滑力τ：

(2)

下滑力：

T=G·sinα

(3)

则作用在塑性区顶面上的有效压应力为最大主应力σ1：

(4)

由于与最大主应力σ1垂直的最小主应力σ3作用方向为临空面，则：

σ3=0

(5)

当塑性区应力满足屈服条件时岩体破坏，即

(6)

将σ1、σ3代入式(6)，简化整理后得

(7)

式中：a为失稳岩体的水平宽度；r为岩体重度；C、φ为结构面的抗剪强度；C′、φ′为岩体抗剪强度；α为结构面倾角。

从顺层边坡溃屈型破坏力学原理的推导过程可以得出，岩质边坡发生此模式破坏必须满足3个条件：存在外倾结构面；结构面倾角较陡，大于或等于坡角；坡脚岩体强度较差。

2 工程实例

2.1 工程概况及参数取值

2.1.1 工程概况

该边坡工程位于重庆市南岸区某房地产开发项目场地内，为一人工开挖而形成的陡倾顺层岩质边坡，组成该边坡的主要岩性为侏罗系中统新田沟组页岩，坡脚部分夹部分砂岩，层面陡倾坡外，层面产状为291°∠71°，页岩层面光滑，节理裂隙发育，主要发育一组缓倾坡内的裂隙，其产状为128°∠28°，该边坡坡脚处页岩呈薄层～片状，岩体质量差。设计时该边坡采用锚杆挡墙进行支护，并设5阶放坡，坡中上部放坡坡率为1∶0.5，坡脚处放坡坡率为1∶0.333，每阶边坡高约8 m，每阶设置宽2 m的马道。施工时，按照逆作法施工的原则，进行边开挖边支护，当边坡开挖接近最后一阶时(高约35 m)，边坡发生了垮塌。边坡现场概貌和边坡的典型剖面如图2、图3。

图2 边坡垮塌概貌Fig. 2 General picture of slope collapse

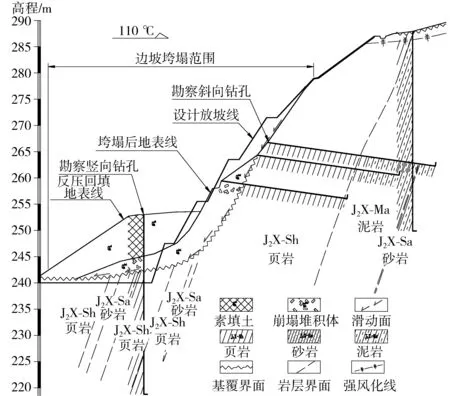
图3 典型剖面Fig. 3 Typical profile

2.1.2 岩体参数取值

据该项目的勘察报告室内试验，同时结合现场实际情况，岩体参数取值如表1。

表1 边坡岩体参数取值Table 1 Calculated parameters of slope rock

2.2 理论计算

根据前面所述顺层边坡溃屈型破坏力学原理，将失稳岩体水平宽度a=5.0 m，岩体重度r=24.64 kN/m3，结构面黏聚力C=25 kPa，结构面内摩擦角φ=12°，岩体黏聚力C′=170 kPa，岩体内摩擦角φ′=30°，边坡坡角71°代入式(7)可以定量计算出边坡极限高度为35.17 m，由计算结果可知，顺层边坡产生“溃屈型”破坏的边坡极限高度约35 m。据勘察资料(如图1、图3)，滑塌块体顶面与底面(剪出口)最大高差36.45 m，边坡开挖高度大于计算得出的极限高度，边坡产生溃屈型破坏，说明计算结果与实际情况基本一致。

2.3 边坡离散元数值分析

2.3.1 计算模型与参数

离散单元法是模拟离散介质大变形和运动趋势的有力工具，特别适用于节理岩体的数值模拟。本次计算运用离散元软件UDEC建立边坡的二维计算模型，计算过程中采用分阶段开挖，以确定分析每个开挖阶段变形情况以及破坏模式。离散元计算模型如图4。

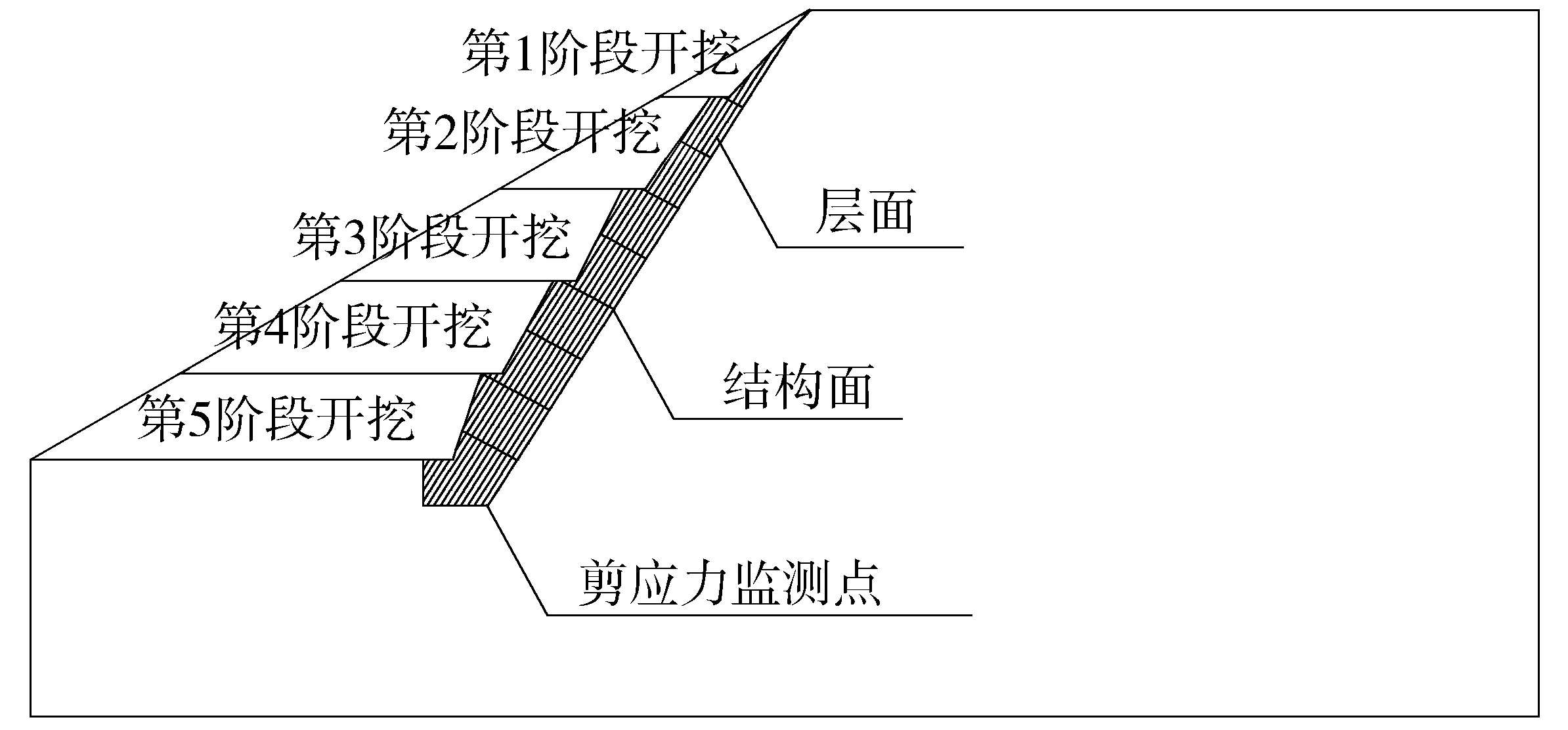
图4 计算模型Fig. 4 Calculation model

根据表1岩体参数确定本次离散元分析计算参数，具体如表2。

表2 计算参数Table 2 Calculated parameters

其中页岩的法向模量K和切向模量G取值依据原勘察报告岩体的弹性模量E=1 187 MPa和泊松比υ=0.31由式(8)、式(9)换算而来：

(8)

(9)

2.3.2 计算结果分析

1) 开挖边坡位移矢量结果

开挖边坡位移矢量结果见图5。从图5可以看出，边坡随着开挖的不断深入，其变形位移量逐渐增大，但边坡的总体位移量很小，当第4阶开挖完成后，总体变形位移最大值为8.356 mm，同时从前4个阶段开挖后的位移矢量箭头方向可以看出，其变形方向主要是指向开挖后的临空面的法向方向，说明其变形主要原因是由于边坡开挖后岩体的卸荷回弹引起的。故边坡在前4个阶的开挖工况下，边坡变形以卸荷回弹为主，边坡未发生明显变形破坏现象，边坡稳定性较好。边坡经过第5阶开挖后，边坡发生了明显的变形破坏现象，在第5阶开挖后，边坡的最大位移量为1.507 m，最大位移主要发生在边坡坡脚部位的岩体，边坡已垮塌。边坡中上部位移矢量图的方向基本与边坡陡倾层面平行，说明边坡的滑动方向主要是沿着层面滑动，而在坡脚处，位移矢量图发生转向，这是由于坡脚岩体发生了屈服，产生了“溃屈”变形，故其位移方向发生了转向。

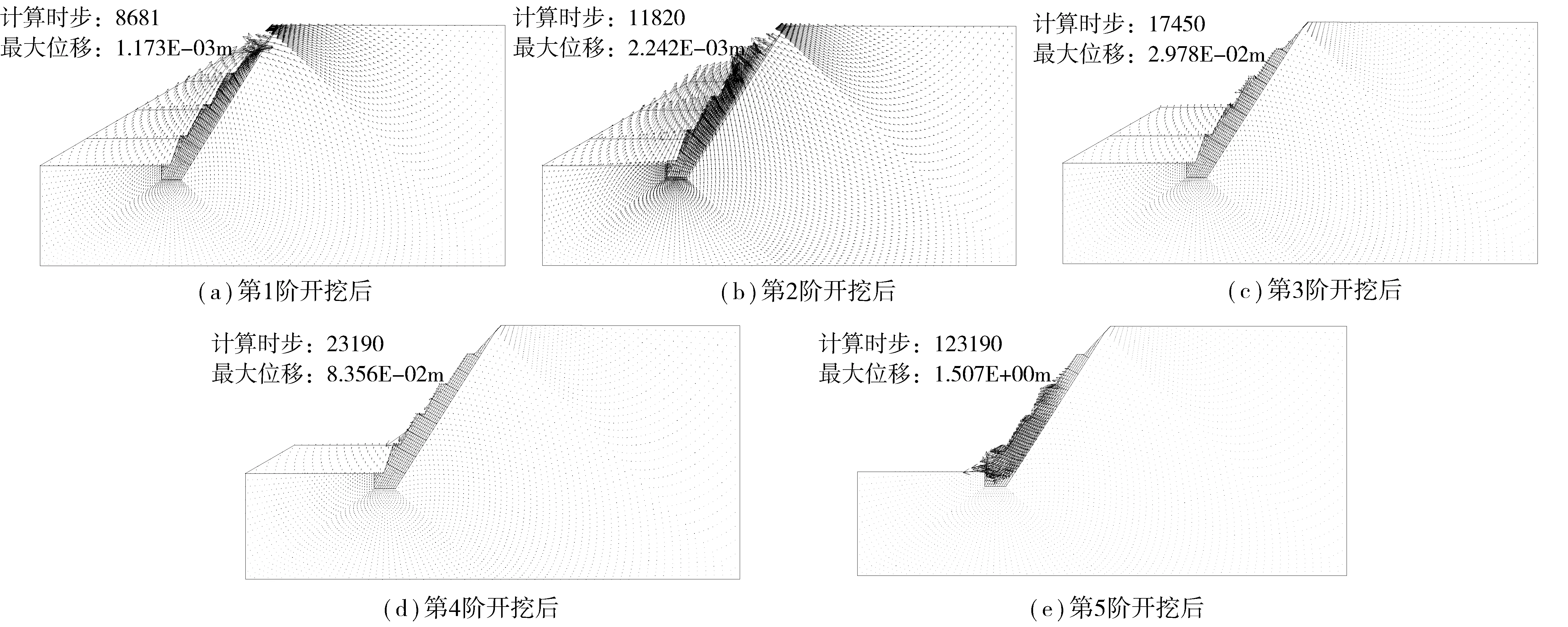
图5 开挖后位移矢量Fig. 5 Displacement vector after stage excavation

2) 开挖边坡剪应力

开挖边坡剪应力云图见图6。从图6可以看出，边坡开挖过程中边坡剪应力变化规律为：从边坡开挖第1阶至边坡开挖第5阶，边坡开挖后其最大剪应力主要集中在坡脚部位，其次随着开挖的不断深入，其坡脚剪应力逐渐增大，坡脚剪应力集中越来越明显，特别是开挖至第5阶时，坡脚剪应力集中加剧，坡脚剪应力越来越大，最终导致边坡坡脚岩体产生了屈服，边坡坡脚发生了“溃屈”变形破坏。

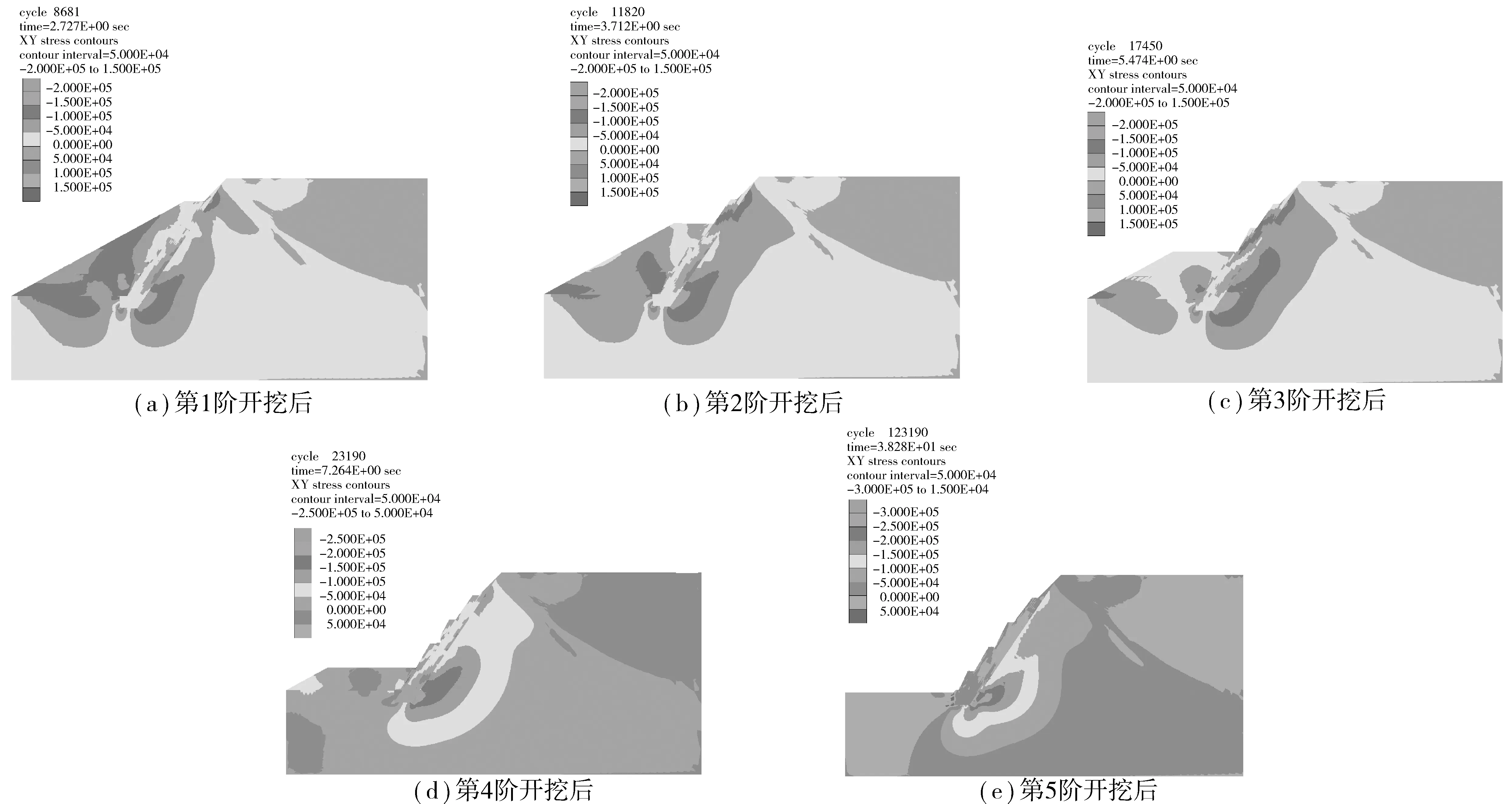
图6 开挖后剪应力云图Fig. 6 Shear stress contour after stage excavation

3) 变形破坏过程

为了进一步展现边坡在第5阶开挖完成后的变形破坏特征，分别给出了第5阶开挖完成后不同时步边坡的变形破坏情况，如图7。从图7中可以看出，边坡开挖至第5阶后，首先是坡脚岩体开始发生屈服，即坡脚岩体开始发生了“溃屈”变形迹象，随着计算时步的进行，边坡这种变形破坏迹象越来越明显，破脚岩体的严重变形为边坡中后部的岩体提供了沿着陡倾结构面滑动的空间，最后边坡发生了垮塌。

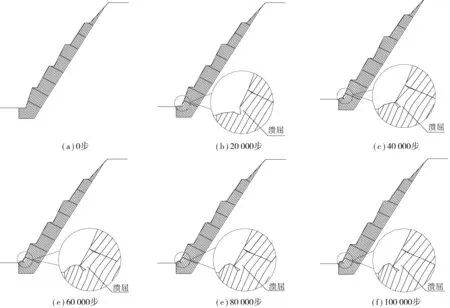
图7 边坡垮塌全过程 Fig. 7 Process of slope collapse

结合理论分析，边坡开挖到第4阶时，虽然开挖坡脚剪应力集中越来越明显，剪应力越来越大，但是剪应力并没有达到使得坡脚岩体发生屈服的“溃屈”变形，也就是边坡没有达到边坡发生溃屈型破坏的极限高度，边坡岩体特别是坡脚岩体处于弹性状态，边坡的变形主要以开挖的卸荷回弹为主，变形方向指向临空面的方向。边坡开挖至第5阶坡底时(开挖深度约36.45 m)，继续增大的剪应力超过了坡脚岩体的抗剪强度，也就是边坡高度达到了极限高度，坡脚岩体处于屈服状态，坡脚岩体首先发生了屈服破坏而产生了较大的位移变形，从而为边坡中上部岩体提供了沿着陡倾坡外的结构面产生下滑的空间，边坡发生了垮塌，模拟结果与现场实际情况(图8)基本一致。

图8 现场边坡坡脚岩体概况Fig. 8 General picture of rock mass at slope foot

3 结 论

笔者首先对顺层岩质边坡溃屈型破坏模型的力学原理进行了探讨，然后结合陡倾顺层岩质边坡的实际工程实例，对边坡的最大极限高度进行了定量的计算，最后通过离散元数值模拟，得出了陡倾顺层岩质边坡发生溃屈破坏的变形破坏过程和变形特征。具体结论如下：

1) 通过陡倾顺层岩质边坡产生溃屈型破坏的力学原理进行探讨，可以得出岩质边坡发生此模式破坏必须满足3个条件：存在外倾结构面；结构面倾角较陡，大于或等于坡角；坡脚岩体强度较差。

2) 结合典型的实际工程实例，运用溃屈型破坏理论计算公式定量计算出了边坡开挖的最大极限高度，计算结果与现场实际情况基本一致。

3) 通过离散元的数值分析，得出了边坡在开挖过程中变形及应力特征，再现了边坡发生溃屈型破坏的具体过程，即：当边坡开挖后，坡脚剪应力集中越来越明显，剪应力越来越大，在边坡未达到边坡发生溃屈型破坏的极限高度时，边坡岩体特别是坡脚岩体处于弹性状态，边坡的变形主要以开挖的卸荷回弹为主，变形方向指向临空面的方向。当边坡高度达到了极限高度，坡脚剪应力增大，使得坡脚岩体处于屈服状态，坡脚岩体首先发生了屈服破坏而产生了较大的位移变形，从而为边坡中上部岩体提供了沿着陡倾坡外的结构面产生下滑的空间，边坡发生了垮塌，理论分析、数值模拟与工程实例之间得到了很好的验证。

参考文献(References)：

[1] 李红卫.陡倾顺层路堑高边坡变形破坏机制分析[J].岩土工程学报，2011，33(增刊1)：153-158.

LI Hongwei.Deformation and failure mechanism of steeply dipping bedding high slopes[J].ChineseJournalofGeotechnicalEngineering，2011，33(Sup1)：153-158.

[2] 夏开宗，陈从新，鲁祖德，等.考虑水力作用的顺层岩质边坡稳定性图解分析[J].岩土力学，2011，35 (10)：2985-2993.

XIA Kaizong，CHEN Congxin，LU Zude，et al.Analysis of stability diagram of rock bedded slope under hydraulic pressure[J].RockandSoilMechanics，2011，35 (10)：2985-2993.

[3] 夏开宗，刘秀敏，陈从新，等.考虑突变理论的顺层岩质边坡失稳研究[J].岩土力学，2015，36 (2)：477-486.

XIA Kaizong，LIU Xiumin，CHEN Congxin，et al.Analysis of mechanism of bedding rock slope instability with catastrophe theory[J].RockandSoilMechanics，2015，36 (2)：477-486.

[4] 胡其志，周辉，肖本林，等.水力作用下顺层岩质边坡稳定性分析[J].岩土力学，2010，31(11)：3594-3598.

HU Qizhi，ZHOU Hui，XIAO Benlin，et al.Analysis of stability of rock bedded slope under hydraulic pressure[J].RockandSoilMechanics，2010，31(11)：3594-3598.

[5] 邓荣贵，周德培，李安洪，等.顺层岩质边坡不稳定岩层临界长度分析[J].岩土工程学报，2002，24(2)：178-182.

DENG Ronggui，ZHOU Depei，LI Anhong，et al.On the critical length of unstable rock stratum on bedrock slope[J].ChineseJournalofGeotechnicalEngineering，2002，24(2)：178-182.

[6] 冯君，周德培，李安洪.顺层岩质边坡开挖模型试验及稳定性影响因素分析[J].工程地质学报，2005，13(3)：294-298.

FENG Jun，ZHOU Depei，LI Anhong.Test and numerical modeling of the stability of rock bedded slope[J].JournalofEngineeringGeology，2005，13(3)：294-298.

[7] 冯君，周德培，李安洪.顺层岩质边坡开挖松弛区试验研究[J].岩石力学与工程学报，2005，24(5)：840-845.

FENG Jun，ZHOU Depei，LI Anhong.Physical modeling research on redlaxation region of consequent rock slope induced by road cutting[J].ChineseJournalofRockmechanicsandEngineering， 2005，24(5)：840-845.

[8] 冯君，周德培，江南，等.顺层岩质边坡顺层滑动岩体范围分析[J].山地学报，2007，25(3)：376-380.

FENG Jun，ZHOU Depei，JIANG Nan，et al.On the extent of bedding Slipping Rockmass of bedding rock slope[J].JournalofMountainScience，2007，25(3)：376-380.

[9] 王智德，夏元友，夏国邦，等.顺层岩质边坡稳定性极限分析上限法[J].岩土力学，2015，36 (2)：576-583.

WANG Dezhi，XIA Yuanyou，XIA Guobang，et al.Upper bound limit analysis method for stability analysis of bedding rock slopes[J].RockandSoilMechanics，2015，36 (2)：576-583.

[10] 李安洪，周德培，冯君.顺层岩质路堑边坡破坏模式及设计对策[J].岩石力学与工程学报，2009，28(增刊1)：2915-2921.

LI Anhong，ZHOU Depei，FENG Jun.Destruction Modes and Designing Countermeasures of Rock Cutting Slope along Strata[J].ChineseJournalofRockMechanicsandEngineering，2009，28(Sup1)：2915-2921.

[11] 李亮辉，余飞，王平，等.顺层岩质路堑边坡稳定性有限元分析[J].岩石力学与工程学报，2004，23(增刊1)：4473-4477.

LI Lianghui，YU Fei，WANG Ping，et al.Finite element analysis of bedding rock slope stability[J].ChineseJournalofRockMechanicsandEngineering，2004，23(Sup 1)：4473-4477.

[12] 肖国峰，冯光乐，陈从新，等.硬岩中倾顺层边坡变形特征和破坏机制分析[J].岩石力学与工程学报，2007，26(增刊2)：4458-4464.

XIAO Guofeng，FENG Guangle，CHEN Congxin，et al.Deformation feature and failure mechanism of inclined plane slope in hard rock[J].ChineseJournalofRockMechanicsandEngineering，2007，26(Sup 2)：4458-4464.

[13] 肖树芳，杨淑碧.岩体力学[M].北京：地质出版社，1987.

XIAO Shufang，YANG Shubi.RockMassMechanics[M].Beijing：Geological Publishing House，1987.

[14] 中华人民共和国住房和城乡建设部门，中华人民共和国国家质量监督检验检疫总局.GB 50330—2013建筑边坡工程技术规范[S].北京：中国建筑工业出版社，2014.

Ministry Housing and Urban-Rural Development of the People’s Republic of China (MOHURD)，General Administration of Quality Supervision，Inspection and Quarantine of the People’s Republic of China.GB50330—2013TechnicalCodforBuildingSlopeEngineering[S].Beijing：China Architecture & Building Press，2014.

[15] 何满潮，黄润秋，王金安，等.工程地质数值法[M].北京：科学出版社，2006.

HE Manchao，HUANG Runqiu，WANG Jin’an，et al.EngineeringGeologicalNumericalMethod[M].Beijing：Science Press，2006.