ARIMA模型在兰州市城关区医院儿科住院的严重急性呼吸道感染病例数预测中的应用

耿文飞，孙晶，黄玲，葛一娴

发热和呼吸系统疾病症状、体征是急性呼吸道感染的主要临床表现，全身或其他系统疾病可由其引起或伴随。住院严重急性呼吸道感染病例(severe acute respiratory infection，SARI)是儿科的常见疾病，对一些免疫力较低的婴幼儿，一旦急性呼吸道感染病原体复杂，发生感染的范围广，感染严重程度较重，通常这些患儿需进入重症监护室(ICU)[1]治疗。国家卫计委自2009年起开展了SARI的监测工作，了解SARI发生情况有助于持续监测新发呼吸道传染病发生。SARI是儿科常见疾病，监测SARI是近年来发现人感染H7N9禽流感、中东呼吸综合征等新发传染病的重要手段，预测SARI的病例数有助于合理安排医疗资源和发现新发呼吸道传染病。

自回归滑动平均混合(autoregressive integrated moving average，ARIMA)模型是ARMA模型的扩展，在流感、甲肝、丙肝等疾病的预测研究和应用表明，该模型与其他时间序列方法(AR、MA、ARMA和指数平滑等)相比能达到较好的拟合效果，在验证集上通常能取得不错的预测效果，与实际值进行比较能较好发现突发情况，对新发疾病和研究疾病的流行过程能起到较好的作用[2-4]。有效预测SARI数状况，合理利用卫生资源对急性上呼吸道感染防控工作的开展具有重要指导意义。本研究利用2010～2016年兰州市城关区人民医院儿科SARI住院资料，通过对p、d、q等参数进行不断调整从而构建ARIMA模型，建立符合我院SARI时间序特点的ARIMA模型，并通过验证集对模型预测效能进行验证，从而确定预测SARI趋势ARIMA模型，为今后我院SARI防控工作提供参考数据。

1 资料与方法

1.1 临床资料 查询兰州市城关区人民医院病案管理系统(hospital information system，HIS)，整理分析2010年1月1日至2016年12月31日本院住院的儿科病历，参考国际疾病(ICD-10)分类编码[5]和SARI病例定义等信息，分月统计符合SARI病例定义的儿科住院患者。

1.2 诊断标准 按照《SARI监测项目方案》的规定：5岁以下患儿急性起病，发热(测量体温≥37.4 ℃)且符合以下条件之一：(1)咳嗽、咽红、呼吸音异常、呼吸频率加快；(2)具有流感样临床表现。

1.3 ARIMA分析方法

1.3.1 以自相关函数(auto correlation function，ACF)和偏自相关函数(partial auto correlation function，PACF) 分析本院SARI时间序列本身以及不同滞后期的自相关、偏自相关系数。其建模过程主要通过如下步骤完成平稳性识别(单位根检验)、模型识别(ACF和PACF)、参数估计(混合自相关图)、模型检验(拟合优度)和比较[6]。根据时间序列的不同可选择模型有MA(q)、AR(p)、ARIMA(p，q)、ARIMA(p，d，q)和ARIMA(p，d，q)×(P，D，Q)s等，其中ARIMA(p，d，q)×(P，D，Q)s为乘积季节模型，为ARIMA模型中最复杂的模型，其模型参数p、d、q以及P、D、Q分别表示非季节模型和季节模型中的自回归的阶、差分(季节差分)次数、滑动平均的阶。ARIMA方法把预测模型分为3个阶段：模型识别、参数估计、拟合检测，通过循环进行ARIMA模型的这三个步骤，最后赤池信息准则(akaike information criterion，AIC)等值判断一个较优的模型用于预测。

1.3.2 通过ACF图和PACF图等方法识别时间序列的平稳性和季节性 如时间序列不平稳性检验，可采用最多3阶的差分方式，使得时间序列较为平稳，将差分后的时间序列进行后期模型识别和其他参数估计[7-8]。

1.3.3 参数的估计 通过混合自相关图(extended autocorrelation function，EACF)确定模型的p、q两个参数，在p、q两个参数存在较多组合的情况下，选择AIC值最小模型作为ARIMA预测模型。模型的质量检验，就是对模型和实际数据的残差进行正态性检验和自相关性检验，较好的ARIMA模型的残差是正态分布(即为白噪声)，并且残差没有相关性。残差经不同阶数的ACF、PACF检验应和0没有显著性差异；时间序列的滞后相关统计量(Box-Ljung Q，LBQ)应没有显著性差异。

1.4 统计学方法 采用R 3.4.0软件，涉及的R语言包有tseries、tidyverse和forecast。通过兰州市城关区人民医院儿科SARI资料进行收集整理，将整理好的时间序列数据集按时间点进行拆分，2010年1月至2016年6月数据作为测试数据集，2016年7～12月数据作为验证数据集，通过模型选择、参数估计、模型检验等步骤构建ARIMA模型。将ARIMA模型获得的预测值与SARI实际值进行比较，计算模型的误差值，误差值越小说明预测越精确。

2 结果

2.1 兰州市城关区SARI数的月分布特征 将兰州市城关区人民医院2010年1月至2016年6月SARI测试数进行分析，观察SARI时间序列图(图1)，可见SARI总体无明显的增长或下降趋势，但还存在同一年内1月和2月SARI病例数低，6月和7月SARI病例数高的周期现象。

图1 2010～2016年兰州市城关区SARI数分布

2.2 平稳性检验 绘制兰州市城关区人民医院2010年1月至2016年6月SARI数的时间序列图。原始序列的ACF图(图2)显示自相关系数下降缓慢，提示该时间序列可能是非平稳序列，对该时间序列进行单位根检验(ADF检验)，P>0.05。由于可能存在季节因素，选择一次非季节差分和一次季节差分后，查分后数据的ACF和PACF图显示差分后的数据平稳，对差分后的数据再次进行数据平稳性检验(ADF检验)，P=0.01。

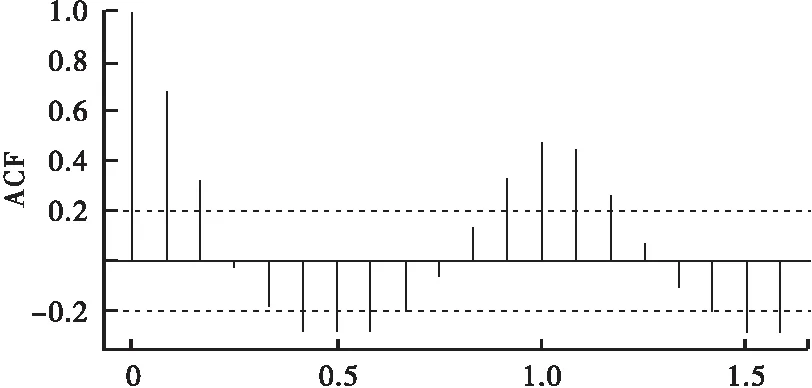
图2 原始序列的ACF图

2.3 ARIMA模型识别 由于在平稳性检验中选择了一次非季节差分和一次季节差分，ARIMA模型d、D参数均为1，由此可确定模型为乘积季节模型ARIMA(p，1，q)(P，1，Q)12。模型中p、q通过eacf获得分别为1和2，P、Q采取从低阶到高阶逐个进行尝试以检验各个模型的拟合优度，并进行比较。选择AIC最小(535.18)的ARIMA(1，1，2)×(2，1，0)12型较优，该模型拟合测试集结果较好平均误差(ME)、均方根误差(RMSE)、平均绝对误差(MAE)、平均百分比误差(MPE)、平均绝对百分比误差(MAPE)、平均绝对定标误差(MASE)、滞后1阶的误差自相关(ACF1)等指标分别为0.34、11.49、7.99、-10.95、31.30、0.76和0.01。

2.4 ARIMA模型诊断 对建立的ARIMA(1，1，2)×(2，1，0)12模型进行残差的正态性检验，结果显示，延迟6阶、12阶、18阶、24阶的LBQ检验统计量的P值分别为0.411 0、0.541 6、0.506 3和0.402 1，说明残差符合正态分布(即为白噪声)；残差的ACF和PACF均提示残差序列为纯随机序列，说明所建立的ARIMA(1，1，2)×(2，1，0)12模型的拟合效果较好。

2.5 模型预测 利用模型ARIMA(1，1，2)×(2，1，0)12预测兰州市城关区2016年6～12月SARI，结果显示2016年6～12月SARI实际值均在该ARIMA模型预测值95%CI范围内(表1、图3)，该ARIMA模型预测的相对误差为22.19%。ARIMA预测值和实际值的动态趋势基本一致，说明了该模型能够准确获得SARI时间序列变化的特点，可以使用该模型对SARI进行跟踪和预测。

表1 ARIMA模型对2016年6～12月兰州市城关区人民医院SARI数预测

3 讨论

近年来由于统计学习取得了迅速发展，在分类和回归的预测上日益准确。在医学领域中，已有马尔科夫、随机森林等多种方法在疾病发病、医院就诊、影像诊断等领域中进行预测[9]。ARIMA模型是比较常用的时间序列预测方法之一，由于其无需相关的自变量并有预测精度高等特点，该方法在各种短期预测中得到了充分的肯定。其中，ARIMA乘积模型是一种复合季节模型，可有效提取时间序列的季节趋势与非季节性成分，提高具有季节特点的时间序列数据的预测精度。已有相关研究证实了ARIMA乘积模型在预测疾病中的可行性与准确性[10]。

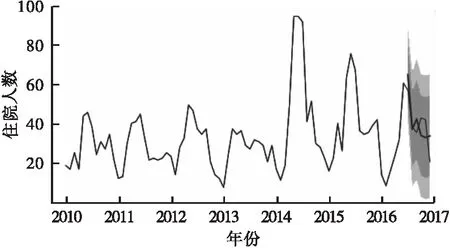
图3 ARIMA模型对2016年6～12月兰州市城关区人民医院SARI数预测

为发现新发急性呼吸道传染病，了解流感等急性呼吸道传染病的临床变化特点，为防控流感等急性呼吸道传染病的传播，根据监测情况国家卫计委每隔几年就调整《SARI哨点监测方案》。本研究利用兰州市城关区2010～2016年数据建立了SARI预测的ARIMA模型，为SARI监测提供给予一定的技术支持和预警。

ARIMA模型无需对时间序列的特征作特定分布的假设[11]，无需其他自变量仅借助时间序列自身的波动特点，使得ARIMA模型应用较广。本研究通过整理2010～2016年兰州市城关区人民医院SARI分月病例数，构建了ARIMA(1，1，2)×(2，1，0)12模型。拟合效果指标RMSE为11.49，MAPE为31.30，表明该模型拟合了数据点范围内的序列特点，提示该模型能在一定程度上能反映出我院SARI病例数的变化规律，可用ARIMA(1，1，2)×(2，1，0)12模型对我院就诊的SARI病例数进预测。2016年7～12月验证数据显示，预测值和实际值比较接近，表明利用ARIMA模型预测兰州市城关区人民医院SARI数的可行性。将该模型进行实际应用后，如果实际SARI病例数在模型预测值95%CI范围内波动，表明当月SARI病例数变化未出现异常情况，如果当月SARI病例数超出预测值95%CI，应引起高度重视提示可能出现新的流行或新发急性呼吸道传染病，这样可以更好地为SARI进行预报及干预提供依据。应用ARIMA模型应注意的是：乘积ARIMA模型建立条件需要达到平稳性的要求，往往通过差分实现序列的平稳性；由于时间序列数据异常波动无法避免，一次分析所建立的ARIMA模型，不能作为永久不变的预测工具[4]，只能用于短期预测。在SARI监测工作中，应不间断的收集的时间序列数据，用新的实际值重新加入时间序列后，重新进行模型的选择、参数估计和模型验证工作，以修正或重新拟合的ARIMA模型进行预测工作。目前，国内尚没有将ARIMA模型进行SARI病例数的短期预测的研究，本研究建立的ARIMA(1，1，2)×(2，1，0)12模型，采用了一次非季节差分和一次季节差分进行数据平稳化处理，通过混合自相关图和AIC值获得了模型最终参数，该模型在验证集预测性能较好。

[1] 彭质斌，郑建东，姜慧，等.全国儿科住院严重急性呼吸道感染病例哨点监测阶段性分析[J].疾病监测，2017，32(1):3-5.

[2] 李琼芬,黄甜,王荣华, 等.传染病疫情预测预警模型研究进展[J].中国公共卫生,2013,29(11):1695-1697.

[3] 龙璐，严薇荣，许奕华，等.症状监测系统预测预警模型研究进展[J].中国公共卫生，2012，28(5):704-706.

[4] 黄利群，谭爱军，张丽荣，等.珠海市2006-2008年流感症状监测分析及预测[J].中国公共卫生，2009，25(8):1013-1015.

[5] 周婧雅,白雪,崔胜男,庞成,刘爱民.我国ICD-10疾病分类编码质量的系统评价[J].中国医院管理,2015,35(12):32-35.

[6] 孙振球.医学统计学[M].3版.北京：人民卫生出版社，2010：391-403.

[7] 刘刚，唐宋，孙文杰．时间序列分析法在香港结核病预测中的应用[J].中国卫生统计，2012，29(2):226-228．

[8] 刘刚，单芙香.ARIMA模型及其在麻疹发病率预测中的应用[J].数理医药学杂志，2011，24(4)：379-382.

[9] 刘桂芬，刘玉秀，仇丽霞，等.医学统计学[M].2版.北京：中国协和医科大学出版社，2009：346-365.

[10]张文增，冀国强，史继新，等.ARIMA模型在细菌性痢疾预测预警中的应用[J].中国卫生统计，2009，26(6):636-637.

[11]Hamilton JD．Time series analysis[M]．New Jersey:Princeton University Press，1994:43-71．