AHP在确定校企合作绩效评价指标权重中的应用

余 红

（广东科学技术职业学院，广东珠海 519090）

1 研究背景及意义

随着《高等职业教育创新发展行动计划（2015—2018 年）》、《关于深入推进职业教育集团化办学的意见》[1]等多项文件的出台，我国职业教育得到了快速发展，人才培养模式也由原来的学校单一办学转变为“校企合作、工学结合”等多元主体办学模式。然而，高职院校将大部分精力放在了如何与企业合作办学方面，在如何评价校企合作办学质量方面的研究较少。

在研究相关文献的基础上，通过对合作项目深入分析，研究和构建校企合作绩效评价指标体系，可以对已经进行的合作项目进行客观、真实地评价。通过评价体系能及时地诊断出存在的问题，为提升校企合作项目质量提供依据；也可挖掘合作潜力，拓展合作空间，促进教育教学改革。

2 评价指标体系的构建

在项目的前期研究中已经应用关键因素分析法和层次分析法设计出了校企合作绩效评价模型, 本文主要研究如何应用AHP来确定校企合作绩效评价指标的权重。

模型将决策问题按总目标层次、关键因素层次和具体绩效指标层次的顺序进行了逐层分解。总目标层1个指标，关键因素层3个指标，具体绩效指标层19个指标。见表1：

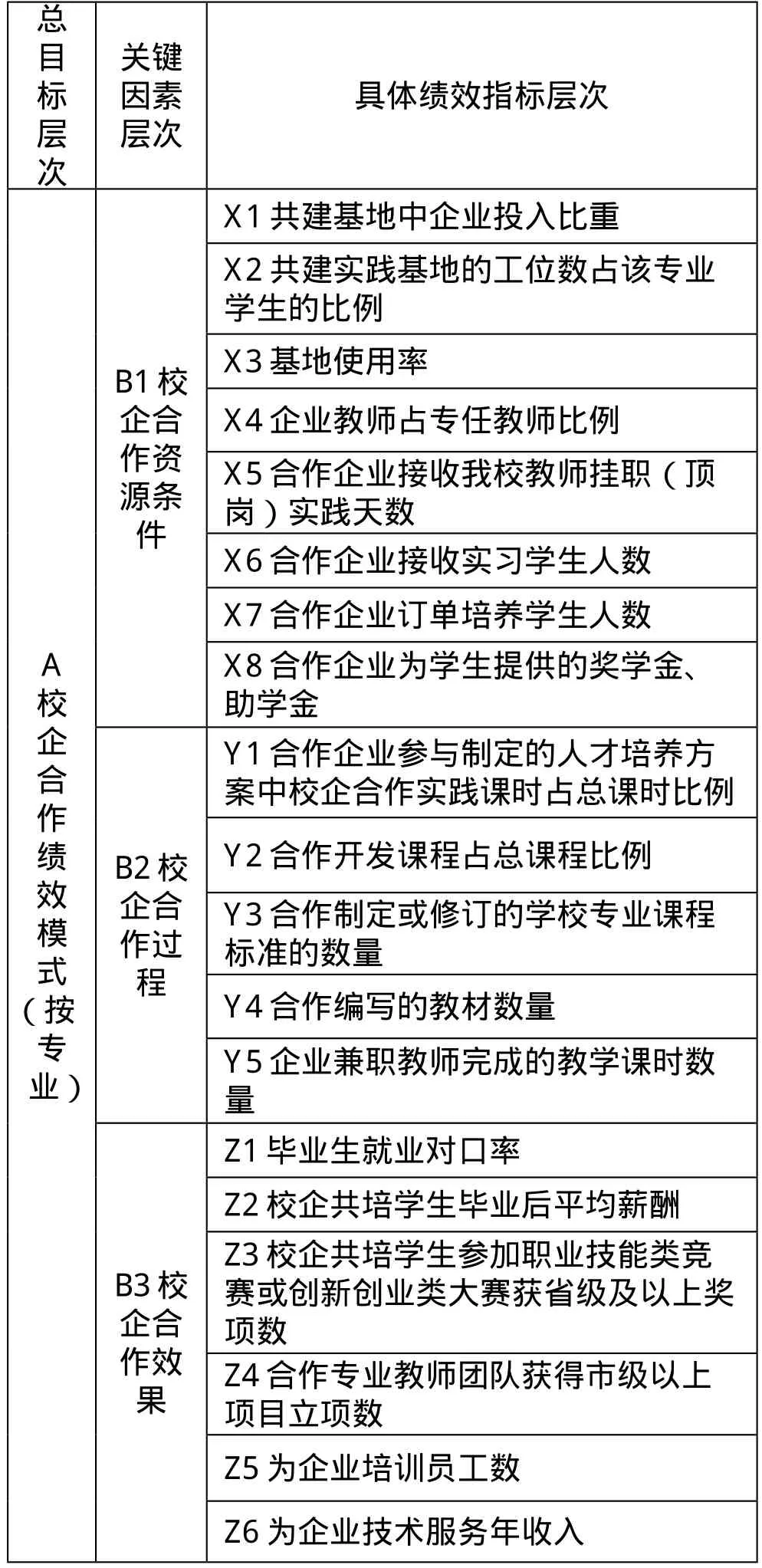
表1 校企合作绩效评价指标

3 指标权重的计算过程

引入九分法来建立指标评价值，并根据评价值设定关键因素层和具体绩效指标层的判断矩阵。

aij = 1，元素i与元素j对上一层次因素同等重要；

aij = 3，元素i比元素j略重要；

aij = 5，元素i比元素j重要；

aij = 7，元素i比元素j重要得多；

aij = 9，元素i比元素j极其重要。

3.1 计算关键因素层指标权重并验证其一致性

（1） 关键因素层构建3个指标对比矩阵A：

（2）计算矩阵的特征向量和指标权重对每一列进行归一化处理，公式如下：

对每一行求和，得出特征向量；再对特征向量进行归一化处理计算出指标的权重，公式如下：

其中：为B矩阵所有行的和， 为i行的和，计算出的三个指标权重如表2：

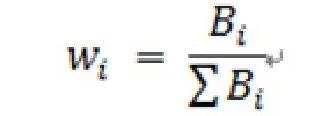
表2 关键因素层3个指标的权重

（3）通过归一化处理我们已经计算出的关键因素层的指标权重，但是权重不一定是有效、可取的，我们还需要检查矩阵的一致性。计算一致性指标的公式如下：

其中AW是矩阵A和矩阵W的乘积，n为矩阵的阶数，关键因素层中n的值为3。CR为平均一致性指标，当CR<0.1时，认为对比矩阵的一致性在可接受范围内，否则，则认为判断矩阵的一致性检测不通过，需要对对比矩阵进行调整。RI是平均随机一致性指标，是一个常量，查表得到n为3时RI为0.58。

由公式（1）计算出

再计算公式（2）

通过计算公式（3）来检验矩阵的一致性，计算结果为,由此可判断矩阵具有相对一致性。

3.2 计算具体绩效指标层指标权重并验证其一致性

具体绩效指标层各指标的相互关系如表3所示：

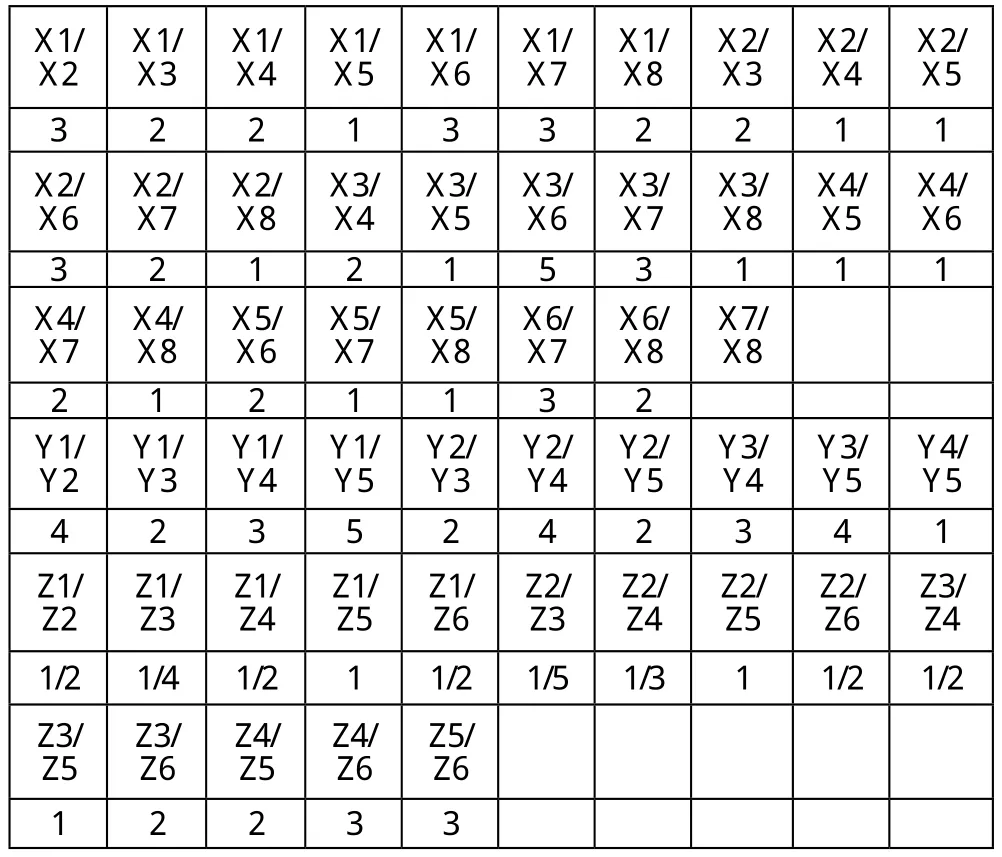
表3 具体绩效指标层各指标间关系

用Excel表计算CI和CR值来检验一致性，X、Y、Z三个矩阵得出的CR值都小于0.1，检验结果通过。各指标权重如表4：

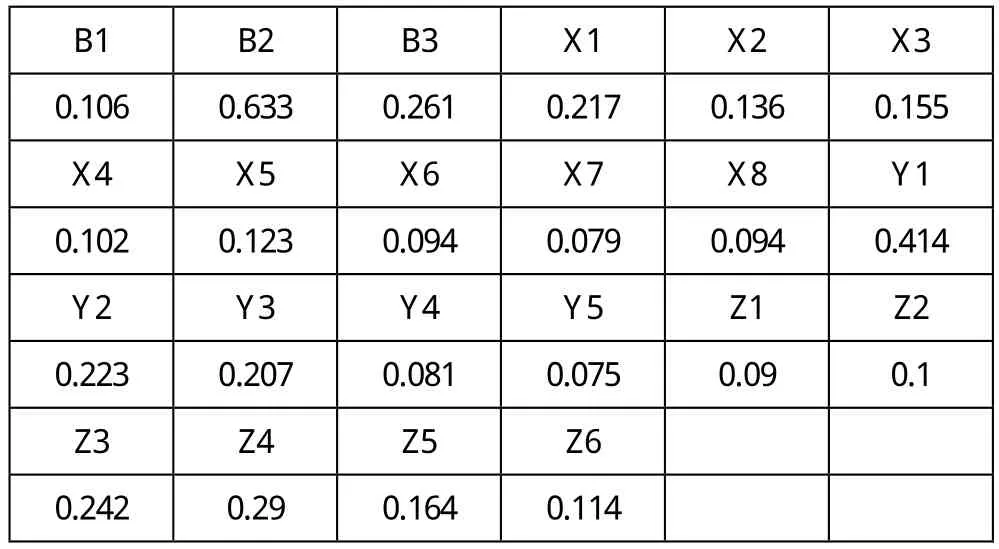
表4 各指标权重

4 结语

高职院校与企业的合作必然要向纵深发展，如何评价校企合作项目的绩效将关系到高职院校人才培养模式改革的质量。本论文运用层次分析法（AHP）构建的校企合作绩效评价体系，具有可量化、操作性强、对合作项目能进行客观、真实地评价等特点。运用该体系来评价合作项目，能及时地为我们正在合作的项目把脉、诊断，促进校企合作的良性循环。

[1] 邱金平.职业院校校企合作绩效评价指标评析[J].科技文汇，2016.5（351）:85-86