关于R-半拓扑空间中连续性的一些结果

靳敏倩， 朱培勇

(电子科技大学数学科学学院， 成都 611731)

引 言

文献[1]给出了一般拓扑空间中连续映射的定义以及等价刻画，2002年，匈牙利数学家ACsaszar[2]提出广义拓扑空间与广义邻域系统的概念，借助这些概念定义了(Ψ，Ψ′)-连续。广义拓扑实际上是一个半拓扑，广义拓扑概念的提出使得学术界开始关注半拓扑空间的研究。近年来，不少学者关于广义拓扑空间的研究已经取得了一系列非常丰富的研究成果，其中文献[3]定义了弱(Ψ，Ψ′)-连续的概念，文献[4]定义了几乎(Ψ，Ψ′)-连续及其等价刻画，进一步丰富了广义拓扑空间连续性的研究。本文借鉴广义拓扑空间连续性的定义方法，在R-半拓扑空间中给出逆开连续、点态连续的定义，以及在R-半拓扑空间中引入(Ψ，Ψ′)-连续、弱(Ψ，Ψ′)-连续与几乎(Ψ，Ψ′)-连续的定义，同时还给出了强(Ψ，Ψ′)-连续的定义，并探究上述各种连续之间的关系。

1 预备知识

定义1[5]设X为一非空集合，λ是X的一些子集构成的集族，称λ是X上一个R-半拓扑，(X,λ)为一个R-半拓扑空间，如果满足以下两条：(O1)φ∈λ;(O2)若Gi∈λ(i∈I)，则∩i∈IGi∈λ(其中I为任一非空指标集)，其中λ中的每个元素称作开集。

定义2设(X,λ)和(X′,λ′)是两个R-半拓扑空间，映射f:X→X′，称f是逆开连续的，如果∀G′∈λ′有f-1(G)∈λ。

定义3设(X,λ)和(X′,λ′)是两个R-半拓扑空间，映射f:X→X′，称f是点态连续的，如果∀V∈((f(x)),∃U∈((x)，使得f(U)⊆V。

定义4设(X,λ)是R-半拓扑空间，映射ψ:X→exp(expX)称为X的R-邻域系统，如果∀x∈X,∀V∈Ψ(x)都有x∈V。其中称Ψ(x)为点x的邻域系，并且Ψ(x)中的每个集合都称为点x的邻域。

定义5设(X,λ)是R-半拓扑空间，Ψ是X上的一个R-邻域系统，A⊆X，则称iΨA={x∈A:存在V∈Ψ(x),满足V⊆A}为A关于Ψ的内部，称γΨA={x∈X:对任一V∈Ψ(x),有V∩A≠φ}为A关于Ψ的闭包。

定义6设(X,λ)设和(X′,λ′)是两个R-半拓扑空间，若Ψ,Ψ′分别是X,X′上的R-邻域系统，映射f:X→X′，称f是(Ψ，Ψ′)-连续，如果∀x∈X,∀V∈Ψ′(f(x))，存在U∈Ψ(x)使得f(U)⊆V。

定义7设(X,λ)和(X′,λ′)是两个R-半拓扑空间，Ψ,Ψ′分别是X,X′上的R-邻域系统，映射f:X→X′，称f是弱(Ψ，Ψ′)-连续，如果∀x∈X,∀V∈Ψ′(f(x))，存在U∈Ψ(x)使得f(U)⊆γΨ′V。

定义8设(X,λ)和(X′,λ′)是两个R-半拓扑空间，Ψ，Ψ′分别是X,X′上的R-邻域系统，映射f:X→X′，称f是几乎(Ψ，Ψ′)-连续，如果∀x∈X,∀V∈Ψ′(f(x))，存在U∈Ψ(x)使得f(U)⊆iΨ′γΨ′V。

定义9设(X,λ)和(X′,λ′)是两个R-半拓扑空间，Ψ，Ψ′分别是X,X′上的R-邻域系统，映射f:X→X′，称f是强(Ψ，Ψ′)-连续，如果∀x∈X,∀V∈Ψ′(f(x))，存在U∈Ψ(x)使得f(U)⊆iΨ′V。

2 逆开连续与点态连续的关系

由文献[1]知，在一般拓扑空间中，逆开映射与点态映射是等价的，在R-半拓扑空间中，逆开映射与点态映射的关系如下：

定理1(X,λ)和(X′,λ′)是两个R-半拓扑空间，若映射f:X→X′是逆开连续，则f:X→X′一定是点态连续；反之不成立。

证明∀x∈X,∀V∈((f(x)),∃G开于X′，使得f(x)∈G⊂V，故x∈f-1(G)⊂f-1(V)，又f-1(G)开于X，则∃U=f-1(G)∈((x)使得f(U)=G⊂V。故f点态连续。

反之，存在R-半拓扑空间(X,λ)和(X′,λ′)，其中X={a,b,c},λ={φ，{a},{a,b},{c},{b}},X′={a′,b′,c′},λ′={φ，{a′},{b′,c′},{c′}}。映射f:X→X′，其中f(a)=a′,f(b)=b′,f(c)=c′。又因为

((f(a))={{a′},{a′,b′},{a′,b′,c′},{a′,c′}}

((f(b))=(〗{b′,c′},{a′,b′,c′}}

((f(c))={{c′},{a′,c′},{b′,c′},{a′,b′,c′}}

((a)={{a},{a,b},{a,c},{a,b,c}}

((b)={{a,b},{b},{a,b,c},{b,c}}

((c)={{c},{a,c},{b,c},{a,b,c}}

容易验证：对∀V∈((f(x)),∃U∈((x)，使得f(U)⊂V，则f为X上的点态连续，但是对X′中开集{b′,c′},f-1({b′,c′})={b,c}不是X中的开集，所以在R-半拓扑空间上，f为点态映射不能推出f为逆开映射。

定理2设(X,λ)和(X′,λ′)是两个R-半拓扑空间，若映射f:X→X′是逆开连续，则有以下五个命题等价：

(1)映射f:X→X′是逆开连续。

(2)若F闭于X′，则f-1(F)闭于X。

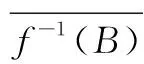
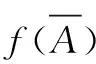
(5)任意的网{xδ}δ∈S⊂X，若xδ→x，则在X′中f(xδ)→f(x)。

证明(1)⟹(5) 任取网{xδ}δ∈S⊂X并且xδ→x。∀V∈((f(x)),∃G开于X′，使得f(x)∈G⊂V，由(1)知f-1(G)开于X且f(f-1(G))⊂V，又因xδ→x，故∃δ0∈S使得∀δ≻δ0有xδ∈f-1(G)。因此f(xδ)∈G⊂V，从而f(xδ)→f(x)。

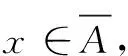
(4)⟹(3) ∀B⊂X′，令A=f-1(B)⊂X，则f(A)⊂B。由

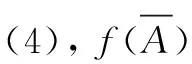
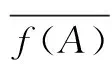
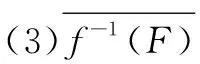
(2)⟹(1) 设G为X′的开集，则F=X′-G是X′的闭集，又f-1(F)=f-1(X′-G)=X-f-1(G)，故f-1(G)开于X。

什么情况下映射f:X→X′是点态连续可以推出f:X→X′是逆开连续。

定理3设(X,λ)和(X′,λ′)是两个R-半拓扑空间，若对∀λ*∈λ有∪λ*∈λ，则f:X→X′是点态连续当且仅当它是逆开连续。

证明由定理1知f:X→X′是逆开连续则一定是点态连续，充分性显然成立。

3 (Ψ，Ψ′)-连续与其他连续的关系

广义拓扑中，文献[2-4]分别给出了(Ψ，Ψ′)-连续、弱(Ψ，Ψ′)-连续与几乎(Ψ，Ψ′)-连续的定义，在R-半拓扑空间中引入上述连续定义，并给出强(Ψ，Ψ′)-连续的定义，进一步讨论几种连续之间的关系。

定理4在R-半拓扑空间中，几乎(Ψ，Ψ′)-连续严格强于弱(Ψ，Ψ′)-连续。

证明先证几乎(Ψ，Ψ′)-连续是弱(Ψ，Ψ′)-连续。由定义8知f(U)⊆iΨ′γΨ′V⊆γΨ′V，所以f:X→X′是弱(Ψ，Ψ′)-连续的。

再证存在映射f:X→X′是弱(Ψ，Ψ′)-连续的，但不是几乎(Ψ，Ψ′)-连续的。事实上，考虑X=X′={a,b,c,d}，定义X、X′上的R-邻域系统Ψ、Ψ′：

Ψ(a)={{a,c}},Ψ(b)={{b,c}},Ψ(c)=

{{c,d}},Ψ(d)={d}

Ψ′(a)={{a,b,c}},Ψ′(b)={{b,c}},Ψ′(c)=

{{c,d}},Ψ′(d)={{a,d}}

定义映射f:X→X′，其中f(a)=a，f(b)=b，f(c)=c,f(d)=d。由定义5可得，γΨ′{a,b,c}=γΨ′{c,d}=X,γΨ′{b,c}={a,b,c},γΨ′{a,d}={a,c,d}。由定义7可知，映射f:X→X′是弱(Ψ，Ψ′)-连续的，但当x=b时，由于V={b,c}∈Ψ′(b),iΨ′γΨ′V={a,b}，而Ψ(b)={b,c}，故不存在U∈Ψ(b)使得f(U)⊆iΨ′γΨ′V，所以f不是几乎(Ψ，Ψ′)-连续的。

互联网企业只有建立科学有效的薪酬体系，才能充分发挥薪酬的激励作用，从而提高员工的工作积极性，增强员工履行职责的责任心。公司对员工付出劳动的回报主要体现在其薪酬体系上，通过发放工资、奖金、津贴等来满足员工的物质需求，从而增强员工对其工作的认可程度，降低员工的跳槽率。

定理5在R-半拓扑空间中，(Ψ，Ψ′)-连续严格强于弱(Ψ，Ψ′)-连续。

证明先证(Ψ，Ψ′)-连续是弱(Ψ，Ψ′)-连续。由定义6知f(U)⊆V⊆γΨ′V，所以f:X→X′是弱(Ψ，Ψ′)-连续的。

再证存在映射f:X→X′是弱(Ψ，Ψ′)-连续的，但不是(Ψ，Ψ′)-连续的。事实上，考虑X=X′={a,b,c,d}，定义X、X′上的R-邻域系统Ψ、Ψ′：

Ψ(a)={{a,c}},Ψ(b)={{b,d}},Ψ(c)=

{{c,d}},Ψ(d)={b,d}

Ψ′(a)={{a,b,c}},Ψ′(b)={{b,c}},Ψ′(c)=

{{c,d}},Ψ′(d)={{a,c,d}}

定义映射f:X→X′其中f(a)=a,f(b)=b,f(c)=c,f(d)=d，由定义5γΨ′{a,b,c}=γΨ′{b,c}=γΨ′{c,d}=γΨ′{a,c,d}=X，由定义7知f:X→X′是弱(Ψ，Ψ′)-连续的。但当x=d时，由于V={a,c,d}∈Ψ′(d)，而Ψ(d)={b,d}，故不存在U∈Ψ(d)使得f(U)⊆V，所以f不是(Ψ，Ψ′)-连续的。

讨论(Ψ，Ψ′)-连续与几乎(Ψ，Ψ′)-连续的关系。

定理6在R-半拓扑空间中，(Ψ，Ψ′)-连续与几乎(Ψ，Ψ′)-连续不能相互推出。

证明先证存在映射f:X→X′是几乎(Ψ，Ψ′)-连续，但不是(Ψ，Ψ′)-连续。事实上，考虑X=X′={a,b,c,d}，定义X、X′上的R-邻域系统Ψ、Ψ′：

Ψ(a)={{a,c}},Ψ(b)={{b,c}},Ψ(c)=

{{a,b,c}},Ψ(d)={{d}}

Ψ′(a)={{a,b,c}},Ψ′(b)={{b,c}},Ψ′(c)=

{{a,c,d}},Ψ′(d)={{c,d}}

定义映射f:X→X′，其中f(a)=a,f(b)=b,f(c)=c,f(d)=d。由于iΨ′γΨ′{a,b,c}=iΨ′γΨ′{b,c}=iΨ′γΨ′{a,c,d}=iΨ′γΨ′{c,d}=X.由定义8知f是几乎(Ψ，Ψ′)-连续的。但当x=c时，由于V={a,c,d}∈Ψ′(c)，而Ψ(c)={a,b,c}，故不存在U∈Ψ(c)使得f(U)⊆V，所以f不是(Ψ，Ψ′)-连续的。

再证存在映射f:X→X′是(Ψ，Ψ′)-连续的，但不是几乎(Ψ，Ψ′)-连续的。事实上，考虑X=X′={a,b,c,d}，定义X、X′上的R-邻域系统Ψ、Ψ′：

Ψ(a)={{a,c}},Ψ(b)={{b,d}},Ψ(c)=

{{a,c,d}},Ψ(d)={d}Ψ′(a)=

{{a,b,c}},Ψ′(b)={{b,d}},Ψ′(c)=

{{a,c,d}},Ψ′(d)={{d}}

定义映射f:X→X′，其中f(a)=a,f(b)=b,f(c)=c,f(d)=d.容易验证，对于∀x∈X,∀V∈Ψ′(f(x))存在U∈Ψ(x)使得f(U)⊆V。当x=a时，f(a)=a.取{a,b,c}∈Ψ′(a),iΨ′γΨ′{a,b,c}={a}，故对∀V∈Ψ′(f(x))，不存在U∈Ψ(x)满足f(U)⊆iΨ′γΨ′V，所以f不是几乎(Ψ，Ψ′)-连续的。

定理7在R-半拓扑空间中，强(Ψ，Ψ′)-连续严格强于(Ψ，Ψ′)-连续。

证明先证强(Ψ，Ψ′)-连续是(Ψ，Ψ′)-连续。由定义9知f(U)⊆iΨ′V⊆V，所以f:X→X′是(Ψ，Ψ′)-连续的。

再证存在映射f:X→X′是(Ψ，Ψ′)-连续的，但不是强(Ψ，Ψ′)-连续的。事实上，考虑X=X′={a,b,c,d}，定义X、X′上的R-邻域系统Ψ、Ψ′：

Ψ(a)={{a,c}},Ψ(b)={{b,d}},Ψ(c)=

{{a,c,d}},Ψ(d)={{d}}Ψ′(a)=

{{a,b,c}},Ψ′(b)={{b,d}},Ψ′(c)=

{{a,c,d}},Ψ′(d)={{d}}

定义映射f:X→X′其中f(a)=a,f(b)=b,f(c)=c,f(d)=d由定义6可知映射f:X→X′是(Ψ，Ψ′)-连续的。但当x=a时，V={a,b,c}∈Ψ′(a)由于iΨ′{a,b,c}={a}，故不存在U∈Ψ(a)使得f(U)⊆iΨ′V，所以f不是强(Ψ，Ψ′)-连续的。

定理8在R-半拓扑空间中，强(Ψ，Ψ′)-连续严格强于几乎(Ψ，Ψ′)-连续。

证明对∀x∈X,∀V∈Ψ′(f(x))，由定义9可知f(U)⊆iΨ′V⊆iΨ′γΨ′V，所以f:X→X′是几乎(Ψ，Ψ′)-连续的。反之不成立。

假设f:X→X′是几乎(Ψ，Ψ′)-连续，则它是强(Ψ，Ψ′)-连续成立，由定理6知f:X→X′是(Ψ，Ψ′)-连续，又由上文知f:X→X′是几乎(Ψ，Ψ′)-连续不能推出f:X→X′是(Ψ，Ψ′)-连续，矛盾，假设不成立。所以若f:X→X′是几乎(Ψ，Ψ′)-连续，则它不是强(Ψ，Ψ′)-连续。

4 结束语

本文借鉴一般拓扑空间与广义拓扑空间连续性的定义，首先在R-半拓扑空间中给出了点态连续和开逆连续的定义，并进一步讨论两者的关系及等价刻画，得出逆开连续一定是点态连续，点态连续不一定是逆开连续的结论。引入(Ψ，Ψ′)-连续、弱(Ψ，Ψ′)-连续与几乎(Ψ，Ψ′)-连续的定义，同时还给出了强(Ψ，Ψ′)-连续的定义，并进一步讨论这几种连续之间的关系，指出：在R-邻域系统上的强连续严格强于连续，连续严格强于弱连续；强连续严格强于几乎连续，几乎连续严格强于弱连续；几乎连续与连续无关。

参考文献：

[1] 朱培勇,雷银彬.拓扑学导论[M].北京:科学出版社,2009.

[2] CSASZAR A.Generalized topology,generalized continuity[J].Acta Math,2002,96(4):351-357.

[3] MIN W K.Weak continuity on generalized topological space[J].Acta Math,2009,124:73-81.

[4] 李阳,朱培勇.关于广义拓扑空间中的几乎连续性的一些结果[J].西南师范大学学报:自然科学版,2016,41(2):36-40.

[5] 钟健,陈道富,朱培勇.关于R-半拓扑空间的一些结果[J].理论数学,2016,6:217-222.

[6] MIN W K.Almost continuity on generalized topological space[J].Acta Math,2009,125:121-125.

[7] CSASZAR A.On generalized neighbourhood systems[J].Acta. Math,2008,121(4):395-400.

[8] CSASZAR A.Generalized neighbourhood[J].Acta Math,2008,124(4):395-400.

[9] MIN W K.Some results on generalized topological spaces and generalized system[J].Acta Math,2005,108:171-181.

[10] SARMA R D.On extremely disconnected generalized topologies[J].Acta Math,2012,134(4):583-588.

[11] CSASZAR A.Generalized open sets in generalized topologies[J].Acta Math,2005,105:53-66.

[12] CSASZAR A.γ-connected sets[J].Acta Math,2003,101:273-279.

[13] CSASZAR A.Separation axioms for generalized topologies[J].Acta Math,2004,104:63-69.

[14] CSASZAR A.Products of generalized topologies[J].Acta Math,2009,123:127-132.

[15] Min WK.Generalized continuous functions defined by generalized open sets on generalized topological spaces[J].Acta Math,2010,128:299-306.

[16] 李瑞佳,朱培勇.拓扑动力系统中强传递集的一些性质[J].四川理工学院学报:自然科学版,2016,29(6):90-93.