Laplace算子的特征函数系在三个空间中的完备性证明方法
2018-06-30邢家省杨义川
邢家省, 杨义川
(1.北京航空航天大学数学与系统科学学院, 北京 100191;2.数学、信息与行为教育部重点实验室, 北京 100191)
引 言
Laplace算子在Dirichlet边界条件下的特征值和特征函数的性质问题[1-11]是偏微分方程中的重要课题,引起了人们持续不断的研究[1-22]。关于特征值的迹问题,在文献[16]中有详尽的综述。对特征函数系的完备性[1-11],已有多种方法给予证明。然而对特征函数系在多个空间中的完备性,现有文献中给出的证明路线不够明确[1-11],甚至出现不严密的表述过程[8],没有达到严密完善的标准程度。本文在前人研究成果的基础上,对特征函数系在三个空间中的完备性分别给予叙述和证明,建立一套标准的证明路线,准确论述了特征函数系的理论结果,推进学术认识发展。
1 Laplace算子在Dirichlet边界条件下的特征值问题
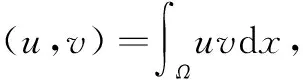

范数记为
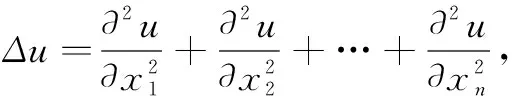
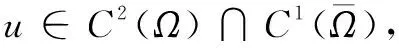
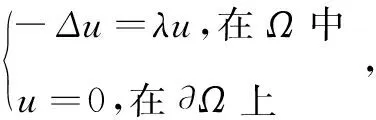
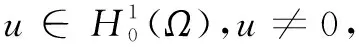
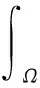
(1)
则称λ为算子-Δ的广义特征值,称u为对应于特征值λ的广义特征函数。
在一定条件下,定义2与定义3是等价的[1-18]。
2 第一特征值问题的存在性
若λ,u是问题(1)的特征值与特征函数,则有
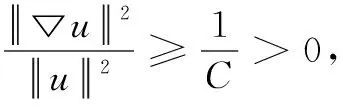
此式说明泛函J(u)有正的下界,因此J(u)有下确界。
定义
(2)
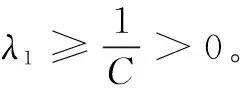
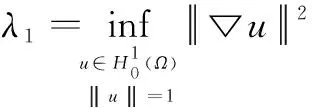
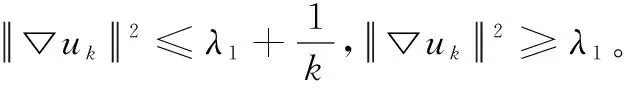
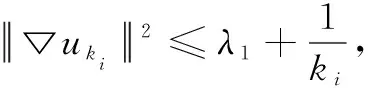
即存在
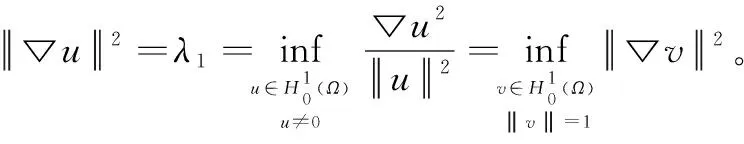
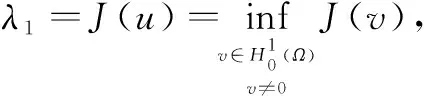
经过展开处理,可得成立
因此,λ1是算子-Δ的特征值,u为对应于特征值λ的特征函数。
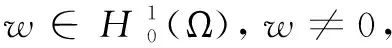
式中,取v=w,得
于是λ1是-Δ的最小特征值。
3 算子-Δ的所有特征值和特征函数系
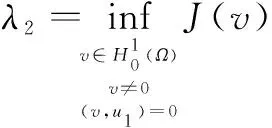
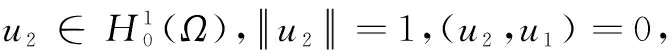
同上可证,λ2,u2满足
即λ2是特征值,u2为对应于特征值λ2的特征函数。
假设已经得出算子-Δ的m-1个特征值,
λ1,λ2,…,λm-1,(m≥1),λ1≤λ2≤…≤λm-1
(3)
对应于λ1,λ2,…,λm-1的特征函数为u1,u2,…,um-1且
(4)
函数组(4)的所有线性组合成为L2(Ω)的一个线性子空间,叫做函数组(4)在L2(Ω)中生成的子空间,记为
Vm-1=span{u1,u2,…,um-1}=
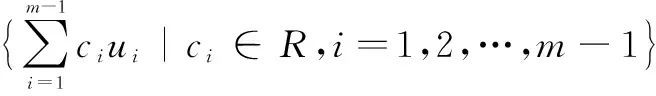
表示Vm-1在L2(Ω)中的正交补空间,即

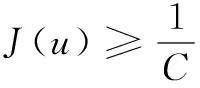
(5)
就是算子-Δ的第m个特征值。
(6)
(7)
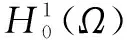
λ1≤λ2≤…≤λm-1≤λm…
(8)
相应的的特征函数序列
u1,u2,…,um-1,um,…
(9)
4 特征值序列{λm}及对应的特征函数系{um}的基本性质
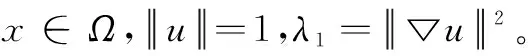
性质2[1-11]对应于不同特征值的特征函数在L2(Ω)中是正交的。
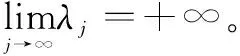
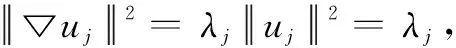
性质4[1-11]对应于同一特征值只有有限个线性无关的特征函数,或者,对应于每一个特征值的特征函数空间是有限维的。
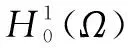
5 特征函数系{um}是空间中的一组正交完备系
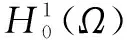
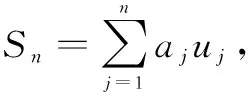
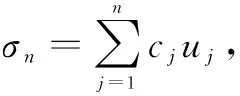
易知
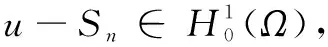
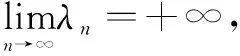
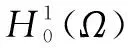
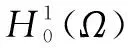
证明
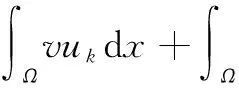
由

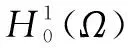
6 特征函数系{um}是空间L2(Ω)中的一组标准正交完备系
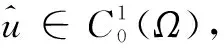
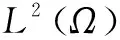
得到{Sn}在L2(Ω)中收敛于u。
7 特征函数系{um}是空间中的一组完备系
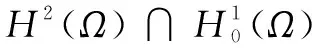
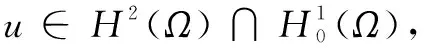
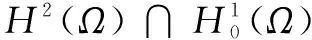
参考文献:
[1] Courant R,Hilbert D,著.数学物理方法(Ⅰ)[M].钱敏,郭敦仁,译.北京:科学出版社,1958.
[2] Smoller J.Shock Waves and Reaction-Diffusions[M].Berlin:Springer-Verlag,1983.
[3] Gilbarg D,Trudinger N S,著.二阶椭圆型偏微分方程[M].叶其孝,译.上海:科学技术出版社,1981.
[4] 叶其孝,李正元.反应扩散方程引论[M].北京:科学出版社,1990.
[5] 陈恕行,洪家兴.偏微分方程近代方法[M].上海:复旦大学出版社,1988.
[6] 陆文端.微分方程中的变分方法[M].北京:科学出版社,2003.
[7] 陈祖墀.偏微分方程[M].合肥:中国科学技术大学出版社,2002.
[8] 张恭庆.变分学讲义[M].北京:高等教育出版社,2011.
[9] 王耀东.偏微分方程的L2理论[M].北京:北京大学出版社,1989.
[10] 张恭庆,林源渠.泛函分析讲义(上册)[M].北京:北京大学出版社,1987.
[11] 丘成桐,孙理察.微分几何讲义[M].北京:高等教育出版社,2004.
[12] 郭柏灵.粘性消去法和差分格式的粘性[M].北京:科学出版社,1993.
[13] 陈国旺.索伯列夫空间导论[M].北京:科学出版社,2013.
[14] 陈国旺,陈翔英.非线性高阶发展方程[M].北京:科学出版社,2017.
[15] 魏光祖,袁忠信,王恩三,等.索伯列夫空间与偏微分方程[M].开封:河南大学出版社,1994.
[16] 曹策问.微分算子的迹[J].数学进展,1989,18(2):170-178.
[17] 唐燕武.Laplace算子的特征函数的正则性[J].安庆师范学院学报:自然科学版,2000,6(4):24-26.
[18] 吴发恩,曹林芬.任意阶Laplace算子的特征值估计[J].中国科学A辑:数学,2007,37(5):587-594.
[19] 定光桂.等距线性延拓问题[J].中国科学:数学,2015,45(1):1-8.
[20] 李上达,周振荣.特征函数的梯度估计[J].华中师范大学学报:自然科学版,2015,49(2):182-185.
[21] 黄俊杰,阿拉坦仓,陈阿茹娜.一类无穷维Hamilton算子特征函数系的完备性[J].应用数学学报,2008,31(3):457-466.
[22] 冯璐,额布日力吐,阿拉坦仓.波动方程混合边值问题的无穷维Hamilton算子辛特征函数系的完备性[J].内蒙古大学学报:自然科学版,2017,48(3):254-258.
