单排微型桩的稳定性计算与受力性能数值模拟

叶忠勤, 肖伦斌, 陶庆东

(1.中国十九冶集团有限公司， 四川 攀枝花 617000；2.绵阳职业技术学院建筑工程系， 四川 绵阳 621000)

引 言

微型桩具有施工速度快、场地占用面积小，组合灵活，避免大面积开挖对环境及地基产生影响的优点，广泛应用于边坡加固工程中[1]。虽然微型桩结构的抗滑力计算与普通抗滑桩结构的设计相同，但由于微型桩是直径一般在100 mm～300 mm，单排微型桩的抗滑能力有限，因此布置在边坡土体的大多数是微型桩群，但群桩和单根微型桩的受力特性存在一定差异。逯卓奇[2]对国内外有关微型桩加固边坡的研究成果进行归纳总结，指出微型桩计算以参考抗滑桩设计方法为主，缺少独立的计算理论，且对微型桩的不同布置方案情况下桩体的受力性能与受力特点的研究较少。王金梅[3]基于微型桩单桩加固边坡时桩体两端的变形规律，提出了微型单桩的理论计算模型，但模型参数较多，不易于实际工程应用。李昌龙[4]以普通抗滑桩设计理论为参考，对比研究了微型桩的计算方法，并通过工程实例参数进行验证与分析，得到了较为完善的计算模型。张东明[5]通过对不同锚固深度的微型桩加固边坡的稳定性进行数值模拟，较为系统的分析了锚固深度对边坡稳定性与桩体内力的影响。陈正[6]运用ABAQUS有限元软件对现场柔性微型桩荷载传递性状、受力特征进行数值模拟，并指出桩长应为桩径的50倍以上。孙书伟[7]建立了微型桩群与普通抗滑桩的模型试验，得到了滑坡推力在不同排微型桩间的分配及微型群桩效应的规律。周德培[8]通过分析坡体上微型桩组合抗滑结构及其组合型式，讨论了微型桩的设计计算过程中应考虑的关键问题及适用条件。屈伟[9]对不同施工工艺微型桩的承载性能进行了试验研究，探讨了二次注浆对单桩及群桩抗拔承载力、桩侧摩阻力、水平承载力提高的敏感性。

虽然对微型桩的研究取得了许多重要的成果，但对单排桩在边坡不同位置的加固机理与安全系数分析的研究并不多。且常见的有限元数值模拟仅考虑桩体-土体之间的摩擦接触对边坡稳定性影响[3-6]。

基于此，通过强度折减计算准则与微型桩切向和法向耦合弹簧准则建立数值模拟模型(切向和法向耦合弹簧准则可以通过程序自动计算桩外边界半径，并考虑该半径范围内土体的材料刚度、粘聚力与内摩擦角对桩土接触面的影响，能更合理布置微型桩的位置与桩体-土体的耦合作用，模拟桩周有效应力及桩体对边坡的加固效果)，研究单排微型桩的受力机理和桩体的布置形式对边坡稳定性影响，探讨微型桩的合理布置方式，提高微型桩结构的使用效率，为微型桩稳定边坡土体提供可靠的设计方案和理论依据。

1 力学计算准则

1.1 强度折减计算准则

对于边坡稳定性的计算，采用强度折减法[10-11]。强度折减法的计算公式：

Cm=C/F

(1)

(2)

式中：C和φ是土体所能够提供的粘聚力或内摩擦角；Cm和φm是维持平衡所需要的或土体实际发挥的抗剪强度对应的粘聚力或内摩擦角；Fr是强度折减系数/安全系数。

1.2 微型桩与边坡土体的力学准则

微型桩与边坡土体之间可以通过切向和法向的耦合弹簧模拟[12-13]。模拟的微型桩单元切向弹簧力学特性如图1所示。模拟的微型桩单元法向弹簧力学特性如图2所示。

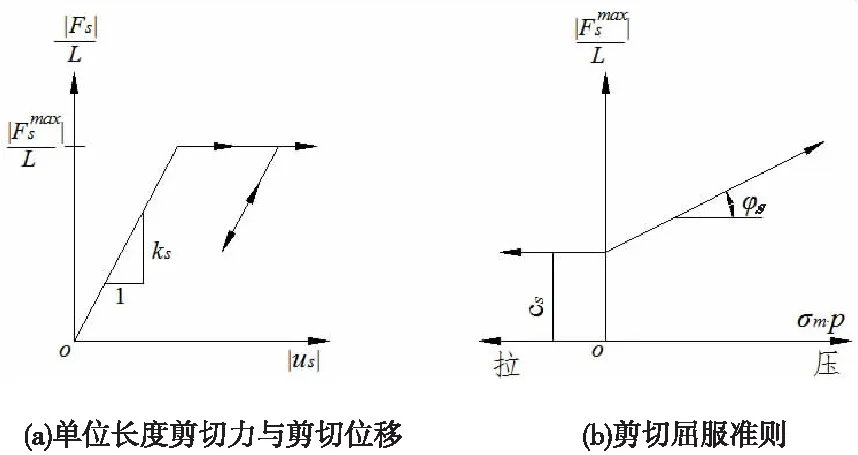
图1 模拟微型桩单元切向弹簧力学特性图

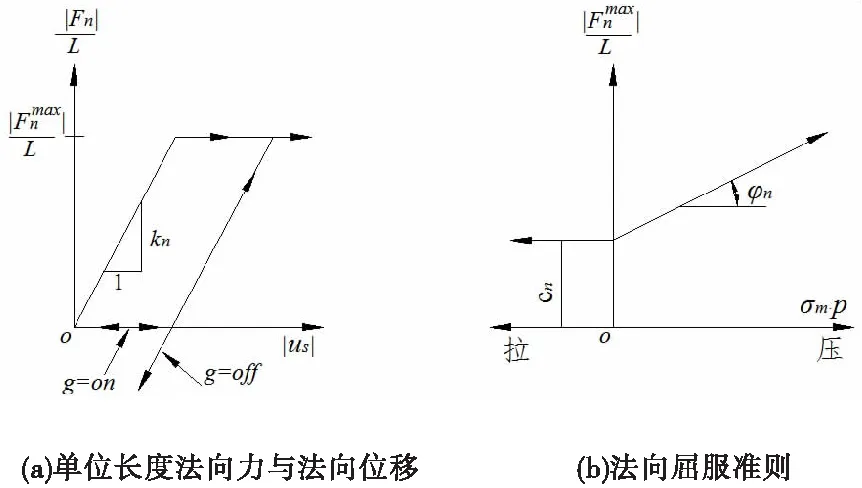
图2 模拟微型桩单元法向弹簧力学特性图

图1、图2中FS/L与Fn/L为模拟的微型桩单元单位长度上的切向力与法向力；CS和Cn为微型桩与边坡土体接触面上的切向与法向粘聚力；φS和φn为接触界面上的切向与法向内摩擦角；P为微型桩横截面的周长；kS和kn为桩的切向和法向的弹簧刚度；σm为桩周土的压应力；g表示微型桩与土法向的两种状态，张开和闭合分别用on和off表示。

1.3 建立岩土材料模型

数值模型中，岩土材料采用修正Mohr-Coulomb模型进行描述，其屈服准则用国内岩土工程公认的Mohr-Coulomb准则(张拉剪切组合)，如图3所示。

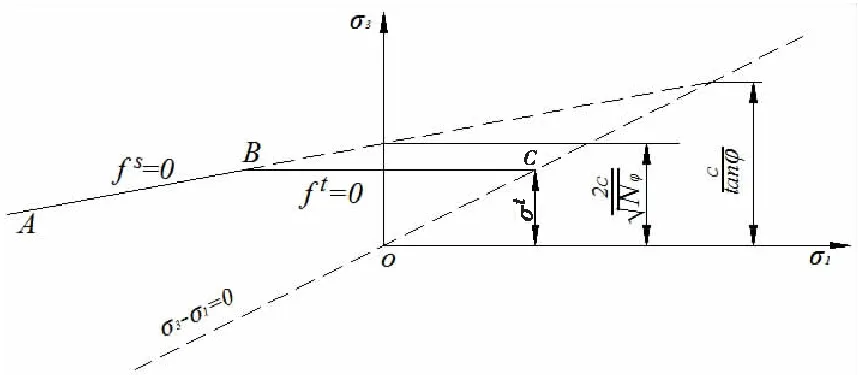
图3 Mohr-Coulomb屈服准则

屈服函数用Mohr-Coulomb屈服准则描述从点A到点B破坏包络线fs=0，即

(3)

用式ft=0张拉破坏准则描述从点B到点C的包络线：

ft=σ3-σt

(4)

式中：φ是摩擦角，c为粘聚力，σt为张拉强度，且有：

(5)

张拉强度不超过σ3值。最大值：

(6)

分别用两个定义剪切塑形流动和张拉塑形流动的函数gS和gt描述势函数。函数gS有：

gS=σ1-σ3Nψ

(7)

(8)

式中：ψ为剪胀角。函数gt符合相关联流动法则，写成

gt=σ3

(9)

1.4 微型桩群结构受力

图4为工程中的竖向微型桩结构简图，当微型桩的布置位置确定以后，可根据桩位处设计安全系数下的下滑力，即微型桩结构应该提供的最小设计抗滑力。

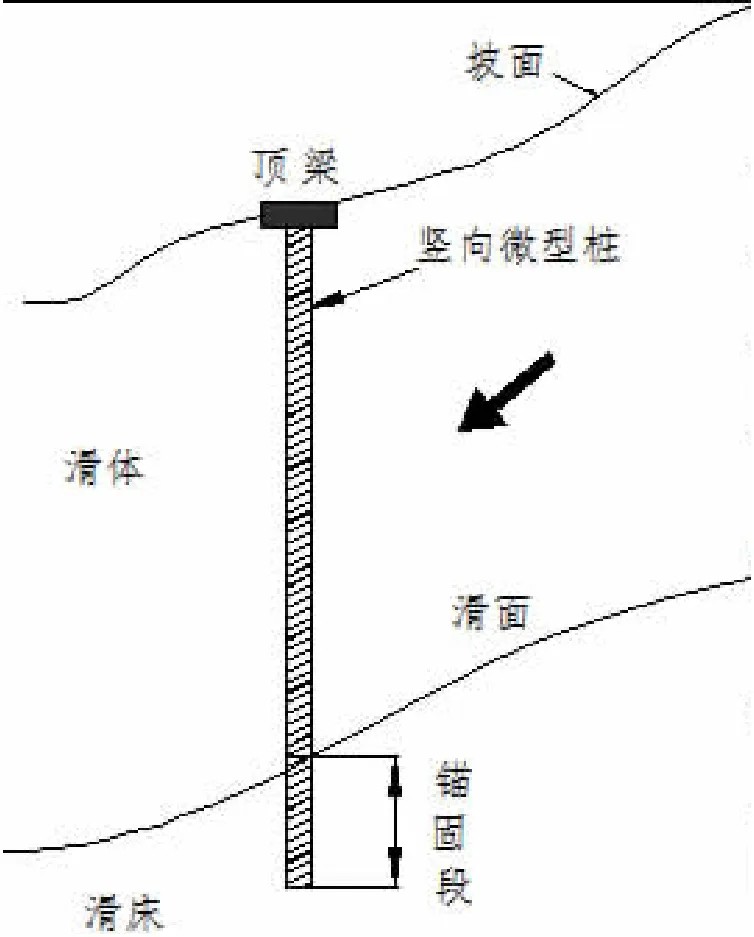
图4 单排竖向微型桩结构简图

微型桩常用的横截面形式如图5所示，桩体内部的加筋体为钢管或螺纹钢，注浆体主要为净水泥浆或水泥砂浆。

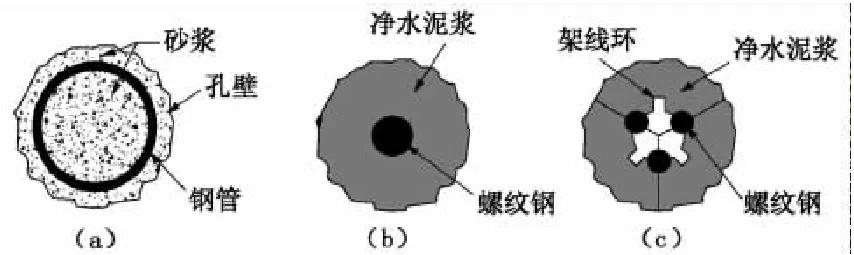
图5 微型桩的横截面形式

根据文献[14]，桩体直径D=1.2 m的抗滑桩在位移作用下产生土拱效应的最大间距(垂直推力方向)S=4D。孔纪名等[15]建立了单排微型桩加固碎石土滑坡物理模型试验，分析了不同桩间距下单排微型桩加固碎石土滑坡的抗滑过程，得到微型桩在碎石土滑坡中的最佳间距为4D。基于此，有限元模型建立的单排桩桩距为S=4D。

2 微型桩受力性能数值模型建立

2.1 微型桩群-边坡模型建立及参数

微型桩-边坡模型如图6所示，桩径为0.2 m，桩间距为S=4D=0.8 m，三维模型的厚度为2S=1.6 m，微型桩的桩长以桩顶端高于边坡坡面、桩底端与边坡坡底齐平计算[16]。

边坡土体模型为理想弹塑形Mohr-Coulomb模型，其中边坡土体采用粘土，具体模型材料参数见表1。为保证桩端与桩端土体、桩身与桩身土体紧密接触，接触面设置成粗糙面，避免土体-桩体发生相互滑动，接触面上设置大小为0.02的摩擦系数，有限元模型如图6所示。

表1 模型材料参数

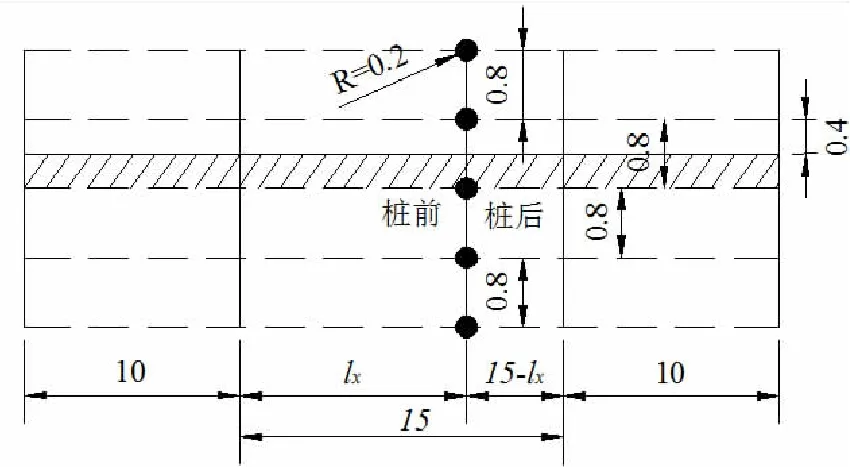
图6 微型桩-边坡模型尺寸

图7 微型桩-边坡有限元模型

2.2 单排微型桩不同桩位数值模拟

模型模拟试验采用单排微型桩，改变微型桩在边坡上的位置，如图7所示。按照lx/l为0，0.2，0.4，0.6，0.8，1.0的方式进行单排微型桩模拟试验，根据五种情况下的安全系数，确定最优的微型桩加固位置。

通过对不同桩位处的微型桩进行数值模拟，得到单排微型桩不同位置的安全系数(表2)。通过表2可知，安全系数随着lx/l的增加，先增大后减小，lx/l为0.6时，安全系数最大，结果表明，对于单排微型桩，将桩体设置在边坡中间部位，边坡抗滑移能力最好。

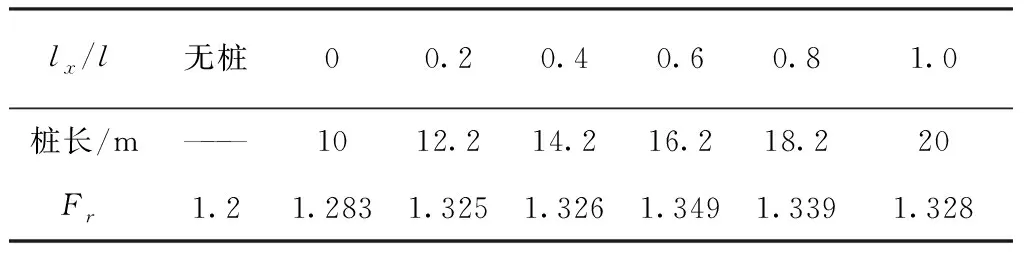
表2 单排微型桩不同位置时的安全系数

图8为单排微型桩-边坡模型位移增量云图，当单排微型桩布置在边坡坡脚(lx/l=0)时，桩体上部的坡体内部产生了整体向下滑移的塑形剪切带，边坡发生了整体滑移；随着lx/l增加，滑动破裂面的位置逐渐向底部扩散，当lx/l=1.0时，破裂面的扩散深度已经较为明显，且破裂面逐渐向微型桩桩体后侧发展；当lx/l为0.2，0.4，0.6，0.8时，边坡滑动破裂面均被切断，坡体原来的整体滑移转变为了局部滑移变形。

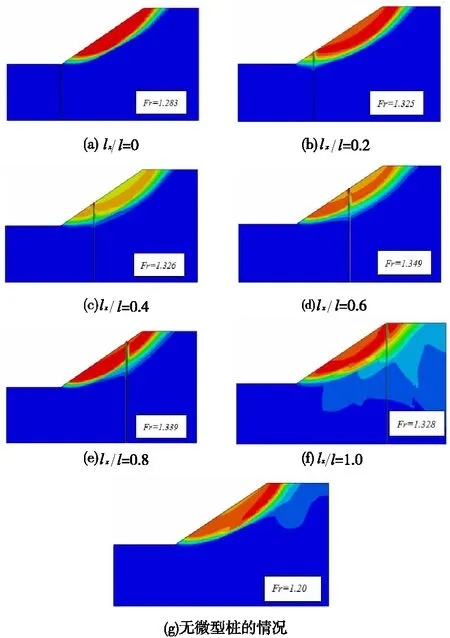
图8 单排微型桩-边坡模型位移增量云图

图9为当lx/l为0.2，0.4，0.6，0.8时，桩体沿土体深度的应力曲线，可以发现桩体应力峰值从大到小顺序的lx/l值为0.6，0.8，0.2，1.0，0.4，表明微型桩布置在边坡中部(lx/l=0.6)，承担边坡滑动的荷载最大，加固效果最为显著；工程施工过程中，由于外界环境或施工设备的因素，微型桩体不能布置在中部时，可以将桩体布置在边坡坡脚上部或坡顶下部0.2倍边坡长度处，以提高微型桩的使用率，减少微型桩的使用数量。

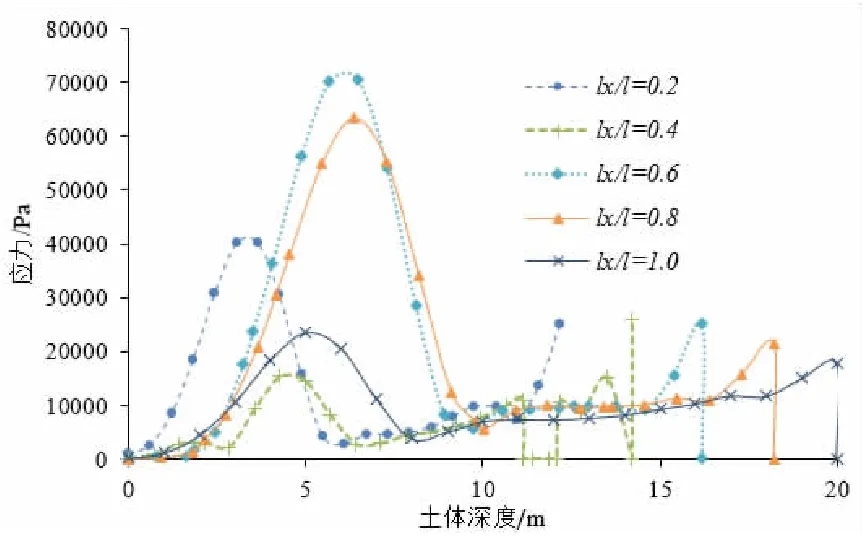
图9 桩体沿土体深度的应力曲线

图10为当lx/l值为0.2，0.4，0.6，0.8时，桩体沿土体深度的水平位移曲线，可以得到桩体水平位移峰值从大到小顺序的lx/l值为0.6，0.8，0.2，1.0，0.4，与桩体应力峰值的排序相同，表明不同微型桩桩位时，桩体承受的荷载与其水平位移成正比例关系；除微型桩在坡脚的位置情况外(微型桩不在边坡上)，其他几种情况下，桩体上出现两个拐点；lx/l值为0.2，0.4，0.6，0.8，1.0时拐点的位置分别为桩顶以下4.27 m和8.52 m，5 m和10 m，7.2 m和10.52 m，8.19 m和11.8 m，6 m和11 m，桩体表现出柔性桩的特性；而lx/l=0时，由于微型桩长度较短，表现出刚性桩的特性。

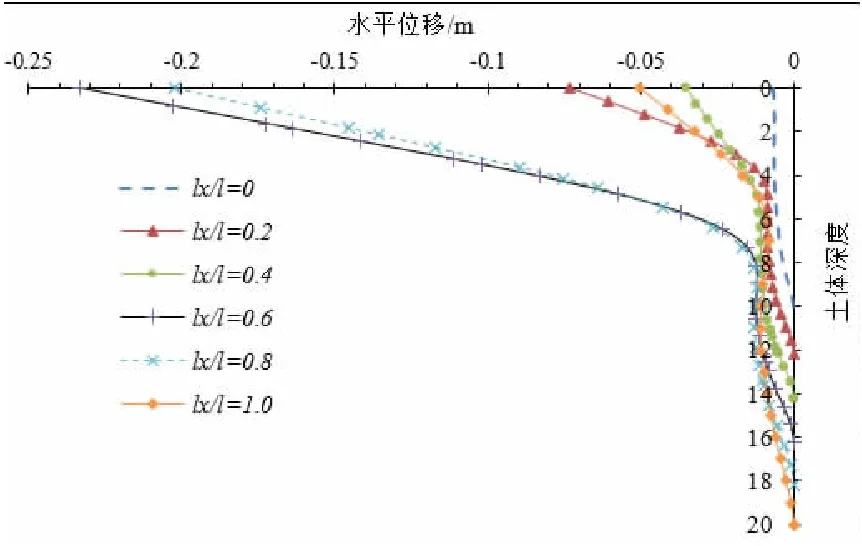
图10 桩体沿土体深度的水平位移曲线

3 结 论

(1)基于强度折减计算准侧和微型桩与切向和法向耦合弹簧准则建立了单排微型桩-边坡抗力分析模型，并将理论模型运用到有限元软件中进行数值模拟。

(2)对不同边坡处的微型桩进行有限元建模，得到随lx/l的增加，安全系数先增大后减小，lx/l为0.6时，安全系数最大，此时微型桩的布置位置为最优加固位置。

(3)当边坡内无微型桩或微型桩布置在边坡顶部与坡脚时，坡体内部产生了整体向下滑移的塑形剪切带，边坡发生了整体滑移；当lx/l为0.2，0.4，0.6，0.8时，边坡滑动破裂面均被切断，坡体由原来的整体滑移转变为局部滑移变形。

(4)微型桩桩体水平位移峰值排序与桩体应力峰值的排序相同，当微型桩布置在边坡上，在桩体上出现两个拐点，桩体表现出柔性桩的特性；当微型桩布置在坡脚，由于微型桩长度较短，表现出刚性桩的特性。

(5)对于微型桩作用下的均质土坡，应考虑微型桩的布置位置与桩体-土体的耦合作用，应避免采用非耦合方法进行滑动面的分析设计。

参考文献：

[1] 孙书伟.微型桩结构加固边坡受力机制和设计计算理论研究[D].北京:中国铁道科学研究院,2009.

[2] 逯卓奇,陈虹旭,王靓露,等.微型桩加固边坡计算理论及试验研究综述[J].公路,2017(5):16-20.

[3] 王金梅,张迎宾,赵兴权.微型抗滑桩单桩设计计算模型及算法研究[J].岩土力学,2015(8):2395-2401.

[4] 李昌龙,姬同旭.承台微型桩系统加固土质滑坡设计计算方法研究[J].中外公路,2017,37(4):17-21.

[5] 张东明,代金鑫,汤伏蛟.微型桩锚固深度对边坡稳定性及桩身内力的影响[J].安全与环境学报,2016,16(2):154-159.

[6] 陈正,梅岭,梅国雄,等.柔性微型桩水平承载力数值模拟[J].岩土力学,2011,32(7):2219-2224.

[7] 孙书伟.微型桩群与普通抗滑桩抗滑特性的对比试验研究[J].岩土工程学报,2009,31(10):1564-1570.

[8] 周德培,王唤龙,孙宏伟,等.微型桩组合抗滑结构及其设计理论[J].岩石力学与工程学报,2009,28(7):1353-1362.

[9] 屈伟,周峰,王一超,等.不同施工工艺微型桩的承载性能试验[J].南京工业大学学报:自然科学版,2015,37(3):91-96.

[10] ZIENKIEWICZ O C,HUMPHESON C,LEWIS R W.Associatedand non-associated visco-plasticity and plasticity in soil mechanics[J].Geotechnique,1975,25(4):671-689.

[11] 刘晓东,张忠平,孙书伟,等.强度折减法在高陡岩质边坡工程中的应用[J].铁道建筑,2012(7):97-99.

[12] 孙书伟,朱本珍,郑静,等.基于极限抗力分析的微型桩群加固土质边坡设计方法[J].岩土工程学报,2010,32(11):1671-1677.

[13] 孙书伟,陈冲,王卫,等.微型桩组合结构加固边坡稳定性耦合分析[J].中南大学学报:自然科学版,2015(10):3774-3781.

[14] KOURKOULIS R,GEOLAGOTI F,ANASTASO-POULOS I,et al.Slope stabilizing piles and pile-groups: parametric study and design insights[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(7):663-677.

[15] 孔纪名,蔡强,张引,等.单排微型桩加固碎石土滑坡物理模型试验[J].山地学报,2013,31(4):399-405.

[16] 李鑫,李昌龙,白明洲,等.桩间距和布桩形式对微型桩受力的影响[J].北京交通大学学报,2017(4):47-54.