基于小波包与CNN的滚动轴承故障诊断

许 理, 李 戈, 余 亮, 姚 毅

(四川理工学院a.自动化与信息工程学院; b.物理与电子工程学院， 四川 自贡 643000)

引 言

滚动轴承故障诊断的常用方法是振动分析法，而采集的轴承振动信号具有非平稳性等特点，使得对其进行特征提取变得比较困难。小波包(Wavelet Packet，WP)时频分析方法能有效提取非平稳信号的时频特征，具有精细的时频分辨率，可以克服小波变换高频低分辨率的缺陷[1]。小波包已经被广泛应用在机械设备故障诊断[2]、地震检测[3]、医学[4]等领域。文献[5]使用小波包对轴承振动信号进行频谱分析，有效提取了轴承的故障特征，且在复合故障中采用小波包分析效果明显优于小波分析。传统的智能识别方法如反向传播(Back Propagation, BP)神经网络等浅层网络隐含层数量少，特征学习的表达能力有限，训练易陷入局部极值[6]。卷积神经网络(Convolutional Neural Network，CNN)通过引入权值共享、局部感知以及池化层对传统的神经网络结构进行优化，具有深层次的体系结构和强大的特征学习能力[7-9]。CNN目前在医学、认知科学和人工智能等领域得到了广泛应用[10]。Zhang[11]等使用卷积神经网络实现了滚动轴承的故障诊断，表明当用足够的训练样本进行训练时，CNN的故障识别效果优于其他方法。张晴晴[12]等将CNN用于语音识别，相比于目前普遍使用的深层神经网络，CNN的识别性能更好，而且降低了模型的复杂度。Chen等[13]将变速箱振动信号的统计特征组成一特征图，作为CNN的输入，通过CNN实现了变速箱故障的诊断识别，并表现出优于其他方法的识别率和效率。

鉴于小波包精细的时频分辨率和CNN强大的特征学习与识别能力，本文提出了一种基于小波包和CNN的滚动轴承故障诊断方法(WPD_CNN)。

1 基础理论

1.1 小波包分解

小波变换对信号中的高频段不再进行分解，具有高频低分辨率的缺陷。而小波包对信号的低、高频部分同时进行分解，提高了总体时频分辨率，解决了小波分解存在的问题。小波包的具体算法如下[14]：

对于给定的正交小波函数Φ(t)与正交尺度函数Φ(t)，那么它们之间的二尺度方程为：

其中，hk为φ(t)对应的低通滤波器，gk为φ(t)对应的高通滤波器。则小波包的分解算法为：

小波包分解的实质就是将信号通过一组正交的低通与高通滤波器，分解得到低频部分与高频部分。然后对分解后得到的两组信号进行进一步的分解，实现信号的均匀分解。

1.2 CNN模型

训练深度学习网络一般都要求样本量在1万以上，如果样本量太少，那么训练出来的模型精度就会比较低，容易出现过拟合现象。Fine-tuning技术解决了少量样本训练分类模型的问题；CaffeNet模型结构如图1所示，它是caffe团队使用大量图片迭代30多万次训练产生的，实现了对1000类图片的识别分类，具有很好的图片分类效果。本文在caffeNet模型的基础上，采用fine-tuning技术训练自己的模型，在深度学习框架caffe的基础上实现CNN模型的训练。

影响模型预测精度的因素有很多，主要有学习率、卷积核的个数与大小、一次用于测试的样本大小batchsize以及dropout层的dropoutratio参数。本文选取的卷积核的个数与大小与caffeNet模型保持一致，不作改变。而deploy.prototxt文件中的基础学习率base_lr要设置很小，本文base_lr设置为0.001。输出层fc8控制着样本的分类数，从图1可看出，caffeNet的分类数为1000，本文修改为5(因为是实现5分类)，为了着重学习，该层的学习率应该设置比较大，包括权重系数w_lr和偏置系数b_lr的两个学习率，本文w_lr的学习率设为10，偏置系数b_lr的学习率设为20。剩下的两个参数batchsize和dropoutratio对于防止过拟合起着关键性的作用，本文重点对这两个参数进行寻优以获得比较理想的模型。

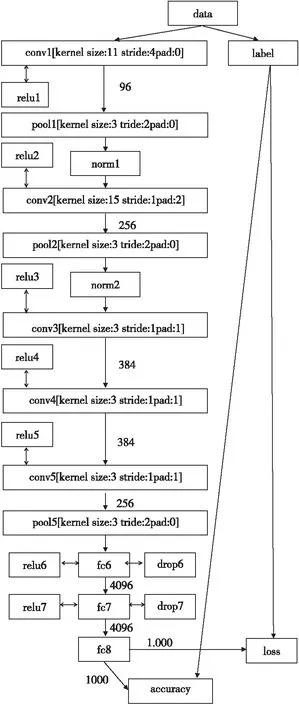
图1 caffeNet模型结构

2 试验数据及结果分析

2.1 数据来源

本文使用的实验数据为凯斯西储大学轴承数据库(Case Western Reserve University, CWRU)的滚动轴承振动加速度数据[15]。采样频率为12000 Hz。实验数据包括轴承四种工况下的振动信号，分为正常信号、滚动体故障信号、内圈故障信号和外圈故障信号。由于轴承运行时经常有复合故障的发生，本文将内、外圈故障信号进行叠加生成内外圈复合故障信号，所以共有五种轴承运行状态。

2.2 数据集准备

每类收集1420个样本，每个样本包含1024个采样点，共收集7100个样本。

训练集：每类信号随机选出1000个样本作为训练集，训练集共包括5000个样本。

验证集：在训练集剩余的样本中，每类信号随机360个样本作为验证集，验证集共包括1800个样本。

测试集：剩余的样本作为测试集，每类60个样本，共包括300个样本。

2.3 故障诊断步骤

(1) 采用小波包对样本集进行时频分析，得到各个样本的特征时频图。

(2) 时频图预处理：调整时频图的尺寸为256×256像素。

(3) 预处理后的时频图作为CNN的输入，采用soft-max作为分类器，训练模型。

(4) 根据模型的测试准确率对CNN网络的参数进行调整，选出一个性能最优的模型，实现故障的分类识别。

2.4 时频分析

机械振动信号大都属于非平稳信号，时频分析在处理非平稳信号方面具有独特的优势，通过时频分析得到的时频图能直观地反映信号时域和频域的综合信息，使振动信号包含的特征信息得到充分展现。本文使用短时傅里叶变换(STFT)、连续小波变换(CWT)和小波包分解(WPD)三种时频分析方法对故障信号进行分析。以外圈故障信号为例，四种分析方法的时频图如图2所示(取1024个采样点，纵轴范围：0～6000 Hz(下同))。

图2 三种时频分析方法的效果图

从图2可以看出，采用STFT得到的时频图，其时间分辨率较低。CWT得到的时频图虽然具有较好的时间分辨率，但其频率分辨率不理想。而采用WPD得到的时频图，其综合的时频分辨率明显优于其他两种分析方法，所以本文采用WPD对滚动轴承信号进行故障特征图提取。预处理后的WPD时频图如图3所示。

图3 预处理后的WPD时频图

2.5 结果分析

2.5.1 dropout参数对结果的影响

分别设置dropoutratio为0.1、0.3、0.5、0.7、0.9进行试验(两个dropout层参数设置相同)，这里batchsize暂取150。图4给出了dropoutratio取不同值时验证集的识别准确率(5次试验取平均值，下同)。从图4可知，当dropoutratio为0.3时收敛速度最快，效果最好。表1给出了测试集的真实识别准确率，从中可知，dropoutratio取0.3识别准确率最高，达到了92%，而dropoutratio取0.1时的外圈故障、取0.7时的内外圈复合故障以及取0.9时的多种故障(内圈、外圈和内外圈复合故障)都出现了严重的过拟合现象。

图4 dropoutratio取值对结果影响的效果图

0.10.30.50.70.9正常1.0001.0001.0001.0001.000滚动体故障1.0001.0001.0001.0000.500内圈故障0.9380.9070.4920.7840.000外圈故障0.0611.000.8921.000.031内外圈复合故障0.9530.6920.7530.0920.000整体准确率0.7910.920.8270.7750.307

2.5.2 批量尺寸batchsize对结果的影响

由2.5.1节可知，dropoutratio取值为0.3时效果最好，所以这里设置dropoutratio为0.3。由于验证集的样本总数为1800，为了使其得到充分利用，选择的batchsize要能被1800整除，因此本文分别取batchsize为90,100,120,150,180,200,225,300进行模型训练。图5给出了验证集的识别结果(为了图片便于观察，仅显示5个效果较好的batchsize)，图6是图5的局部放大图。从中可知，5种情况下训练的模型都能迅速收敛，batchsize取200时收敛速度最快(图中黑色实线)，准确率最高。表2给出了对五种工况进行测试的真实准确率，当batchsize=200时，识别的准确率最高，达到了99.1%。

综上所述，参数dropoutratio和batchsize对故障识别的准确率有很大的影响，本文采用网格法对这两个参数进行寻优，寻优后参数dropoutratio值为0.3(两dropout层一样)，batchsize值为200.最终滚动轴承故障诊断的识别率为99.1%.

图5 batchsize取值对结果影响的效果图

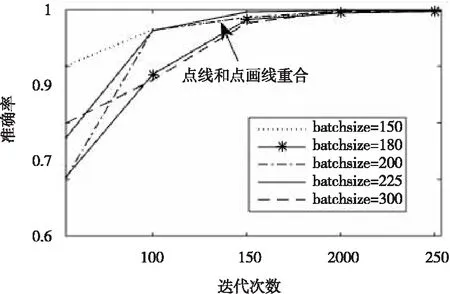
图6 图5的局部放大图

150180200225300正常1.0001.0001.0001.0001.000滚动体故障1.0001.0001.0001.0001.000内圈故障0.9230.9230.9690.8610.784外圈故障1.0000.9691.0001.0000.861内外圈复合故障0.6920.9230.9840.8000.969整体准确率0.9230.9630.9910.9320.923

2.5.3 PCA_SVM与CNN识别结果对比

PCA_SVM故障诊断用到的训练集和测试集同2.3小节，每个样本包含1024个采样点。采用PCA算法对样本进行压缩降维，为了使主成分的贡献率在 95% 以上，每个样本由1024维降到了15维。最后采用SVM对样本进行训练和故障识别，识别结果见表3(5次实验取均值)。

表3给出了多种识别算法的识别准确率，采用CNN算法分别与STFT、CWT和WPD相结合，模型的准确率都明显优于PCA_SVM。采用CWT和WPD对滚动轴承信号进行时频分析，得出的CNN识别率高于STFT。而采用WPD_CNN算法对轴承的故障识别率最好，达到了99.1%。

表3 多种识别算法的预测准确率对比

3 结束语

利用WPD综合时频分辨率优于STFT和CWT的特性，结合CNN强大的特征提取能力，提出了一种基于WPD与CNN相结合的滚动轴承故障诊断方法。通过参数寻优和模型训练，找到了比较理想的用于轴承故障诊断的模型。通过与多种故障识别算法对比分析可知，本文提出的WPD_CNN算法对轴承的故障识别的准确率最高。

参考文献：

[1] 王红军,万鹏.基于EEMD和小波包变换的早期故障敏感特征获取[J].北京理工大学学报,2013,33(9):945-950.

[2] 肖顺根,宋萌萌.基于小波包能量神经网络的滚动轴承故障诊断方法[J].机械强度,2014,36(3):340-346.

[3] SU W C,HUANG C S.Identification of structural stiffness parameters via wavelet packet from seismic response[J].Procedia Engineering,2017,199:1032-1037.

[4] SILVEIRA T L T D,KOZAKEVICIUS A J,RODRIGUES C R.Automated drowsiness detection through wavelet packet analysis of a single EEG channel[J].Expert Systems with Applications,2016,55:559-565.

[5] YANG Z,GAO L.Wavelet analysis and fault feature extraction of rolling bearing[M].London:Springer London,2014.

[6] 刘春艳,凌建春,寇林元,等.GA-BP神经网络与 BP神经网络性能比较[J].中国卫生统计,2013,30(2):173-176.

[7] 陈锐,林达.基于级联卷积神经网络的人脸关键点定位[J].四川理工学院学报:自然科学版,2017,30(1):32-37.

[8] ABDEL-HAMID O,MOHAMED A R,JIANG H,et al.Convolutional Neural Networks for Speech Recognition[J].IEEE/ACM Transactions on Audio Speech & Language Processing,2014,22(10):1533-1545.

[9] KIM Y.Convolutional Neural Networks for Sentence Classification[J].Eprint Arxiv,2014.DOI: 10.3115/v1/D14-1181.

[10] 龙飞,王永兴.深度学习入门与实践[M].北京:清华大学出版社,2017.

[11] ZHANG W,PENG G,LI C.Rolling element bearings fault intelligent diagnosis based on convolutional neural networks using raw sensing signal[M].Berlin:Springer International Publishing,2017.

[12] 张晴晴,刘勇,潘接林,等.基于卷积神经网络的连续语音识别[J].工程科学学报,2015,37(9):1212-1217.

[13] CHEN Z Q,LI C,SANCHEZ R V.Gearbox fault identification and classification with convolutional neural networks[J].Shock and Vibration,2015(2):1-10.

[14] FEI M,PENG C,SU Z,et al.Computational Intelligence,Networked Systems and Their Application[M].Berlin:Springer Publishing Company,2014.

[15] LOPARO K. Bearing vibration data set[D].Cleveland:Case Western Reserve University,2003.