变厚齿轮的锥形蜗杆砂轮磨削方法

李国龙，蒋 萍，操 兵，何 坤

(1.重庆大学 机械工程学院 机械传动国家重点实验室，重庆 400044；

0 引言

变厚齿轮是渐开线变齿厚齿轮的简称，其齿厚沿轴线呈规律性变化，在啮合传动时可以调整齿侧间隙，并可实现小倾角传动，具有承载力大、传动平稳、噪声小和占用空间小等特点。变厚齿轮有交错轴、相交轴和平行轴3种传动形式，广泛用于四轮驱动齿轮箱、船用变速箱、精密机器人、全驱动汽车等领域，不同使用环境可以设计不同参数的变厚齿轮副以满足传动条件。由于变厚齿轮的多用途和可能性，使其成为齿轮传动中关注和研究的目标，具有广阔的应用前景，在齿轮传动中具有重要地位[1]。普通圆柱齿轮可看作是齿厚变化为零的变厚齿轮，但是相比于普通圆柱齿轮成熟的各类加工工艺，变厚齿轮的精密磨削加工较为困难，大大限制了变厚齿轮的工业推广应用。

Mitome[2-3]研究了采用Niles型进给研磨、工作台滑动进给研磨和倾斜工作轴进给研磨等方法加工变厚齿轮，认为台式滑动进给研磨最实用；贺敬良等[4-5]对变厚齿轮的展成磨与成形磨进行了探讨，给出了在数控锥面砂轮磨齿机、滚齿机上加工变厚齿轮的方法，其中锥面砂轮磨削斜齿轮时，将左右齿面分开磨削能达到较高精度；王光建等[6]研究了以最小啮合角为优化条件，变厚齿轮副变位系数的计算方法和设计方法；Brecher等[7-9]通过仿真分析了加工参数对变厚齿轮性能的影响，表明制造工艺对变厚齿轮的传动性能有决定性的影响，提出以质量与稳定为优化目标，将制造偏差与公差范围列入优化条件来设计变厚齿轮的微观几何形态；黄金利[10]研究了渐开线与非渐开线空间变厚齿轮副的滚齿加工方法，指出一些公司已成功开发了直齿变厚齿轮的加工方法，如意大利的Somaschini公司、德国的KG公司和ZF公司等；Zimmer等[11]提出变厚齿轮的齿面几何计算方法，通过改变刀具廓形或刀具轨迹规划来设计变厚齿轮的表面；朱才朝等[12-14]分析了多种传动形式的变厚齿轮副啮合特性，通过建立节圆锥模型，讨论锥角、安装误差和载荷等对啮合接触区域的影响；Amani等[15]在渐开线齿轮设计中考虑其可制造性,包括干涉，以及压力角、齿顶高、齿根、齿顶圆角半径和同时参与啮合的齿数等的联合效应。总体来看，有关变厚齿轮的研究大都集中在啮合特性分析、齿厚变化规律设计和仿真建模方面，对变厚齿轮的加工方法研究较少，且大多停留在滚齿加工，精密加工局限于直齿变厚齿轮磨削。目前，变厚齿轮精加工方法主要有大平面磨和圆柱蜗杆砂轮磨两种。圆柱蜗杆砂轮磨削方法采用蜗杆砂轮的一段圆弧型面近似加工出变厚齿轮的廓形，理论上只有一个加工出的截面廓形准确，其他截面都存在误差，且离精确廓形截面越远，误差越大；大平面磨的加工精度有所提高，但因采用单齿逐一展成磨削，故效率较低，且仍存在加工原理误差。

随着对变厚齿轮加工精度、成本及效率等的要求越来越高，变厚齿轮的精密、高效加工工艺缺失已成为制约其应用的瓶颈。为此，本文提出基于锥形蜗杆砂轮的创新性变厚齿轮连续展成磨削工艺，该工艺对于提升变厚齿轮的加工精度、效率具有较为重要的理论意义和实际应用价值。

1 锥形蜗杆砂轮连续展成磨削的运动几何学分析

相比于圆柱蜗杆砂轮磨，本文提出的锥形蜗杆砂轮磨削工艺具有不同的运动几何学特性。从本质上看，圆柱蜗杆砂轮磨为锥形蜗杆砂轮磨的特例，即可以看作锥度为零的锥形蜗杆砂轮磨。为此，需要建立锥形蜗杆砂轮的运动几何学模型，以为锥形蜗杆砂轮磨削的实际应用提供理论支撑。

1.1 变厚齿轮的产形齿条

要进行锥形蜗杆砂轮磨削建模，必须先分析变厚齿轮工件的几何特性。变厚齿轮在垂直于其轴线的各剖面上形渐开线齿形的变位系数一般呈线性变化，齿顶面与齿底面为圆锥型面，其几何特点明显。下面主要分析变厚齿轮的产形齿条特性，以便基于产形齿条中间平面原理进行锥形蜗杆砂轮磨削建模。

建立如图1所示的产形直齿条，齿条分别相对于坐标系的YOZ和XOZ竖直平面的倾斜角为βc、变厚齿轮轴向后角为αp。图中P平面平行于变厚齿轮螺旋线，且经过产形齿条几何中心。产形齿条在P平面内的锥角设为θ，θ与齿条齿形角的计算有重要关系，其与参数αp，βc的关系为

tanθ=tanαpcosβc。

(1)

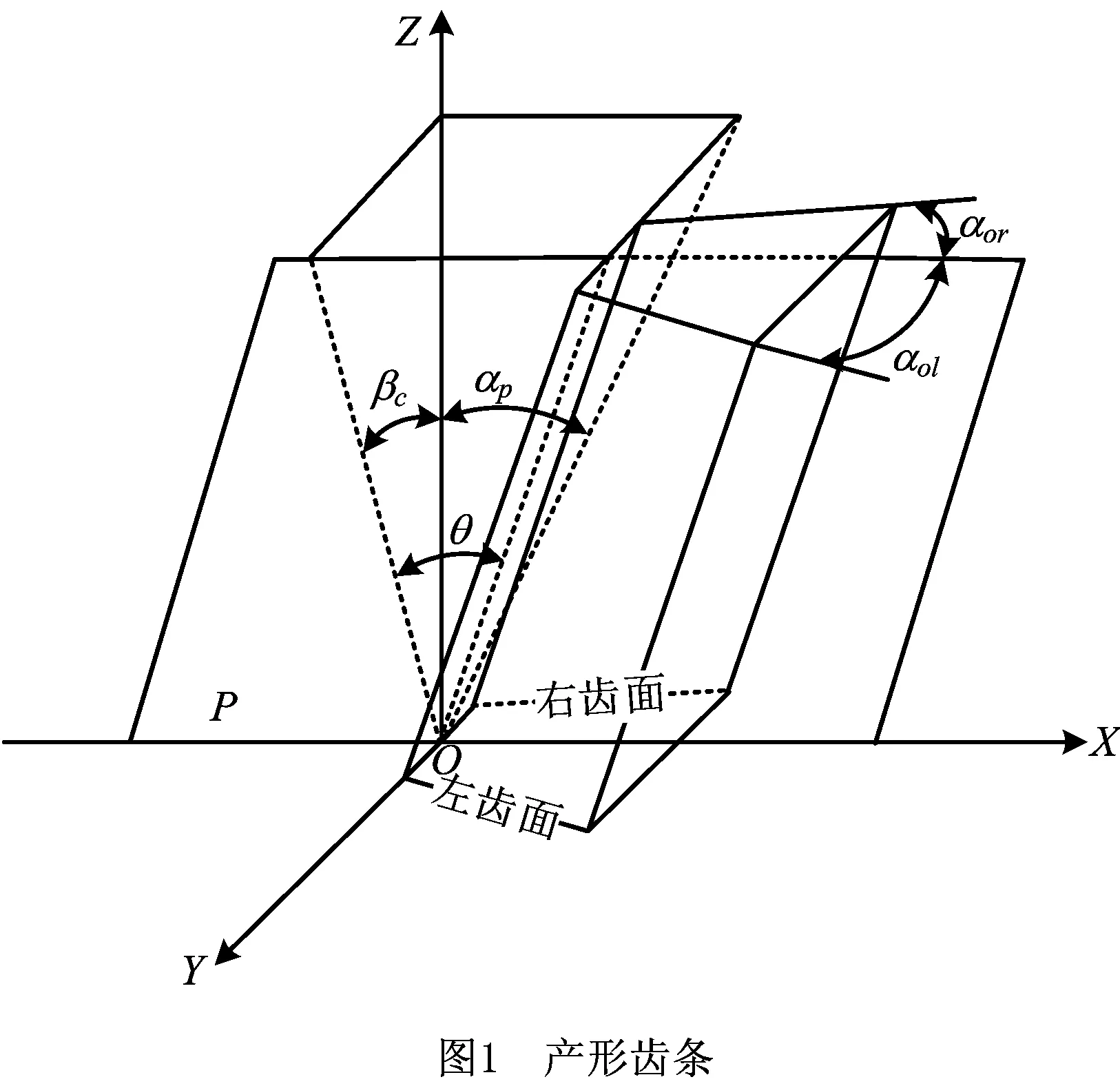
图中αol，αor分别是产形齿条左右齿面在水平面上的齿形角，设变厚齿轮法向分度圆压力角为αn，则

(2)

(3)

不论齿轮如何变位，变厚齿轮齿条啮合的节圆半径始终不变。因此，变厚齿轮与产形齿条啮合时节圆半径不随轴向距离变化，而恒与分度圆重合；并且产形齿条的节线与分度线不重合，节面上左右侧螺旋角也各自不同。

1.2 锥形蜗杆砂轮的数学模型

将上述产形齿条作为变厚齿轮与蜗杆砂轮的中间平面，蜗杆砂轮与产形齿条为线接触，产形齿条展成加工齿轮时也为线接触，两条接触线相交的点为蜗杆砂轮与齿轮的接触点。如图2所示，设O′为垂直的产形齿条分度面，O为变厚齿轮的产形齿条分度面，其相对于垂直面倾斜了一个角αp。S为蜗杆砂轮轴向齿廓平面，砂轮轴线的安装角设为Γ。S与O′的交线AC与蜗杆砂轮轴线平行，且为砂轮的分度圆柱母线，而与倾斜的分度面O相交于斜线AD，为了保证蜗杆砂轮与该产形齿条啮合时为线接触，AD应为砂轮分度圆面母线。可以看出，只要O倾斜，AD与AC肯定不平行，AD与轴线也不平行，在轴截面S内必有一夹角γ，因此加工变厚齿轮的蜗杆砂轮分度圆面为锥角γ的圆锥面，产形齿条齿面由蜗杆砂轮轴向齿廓包络而成。

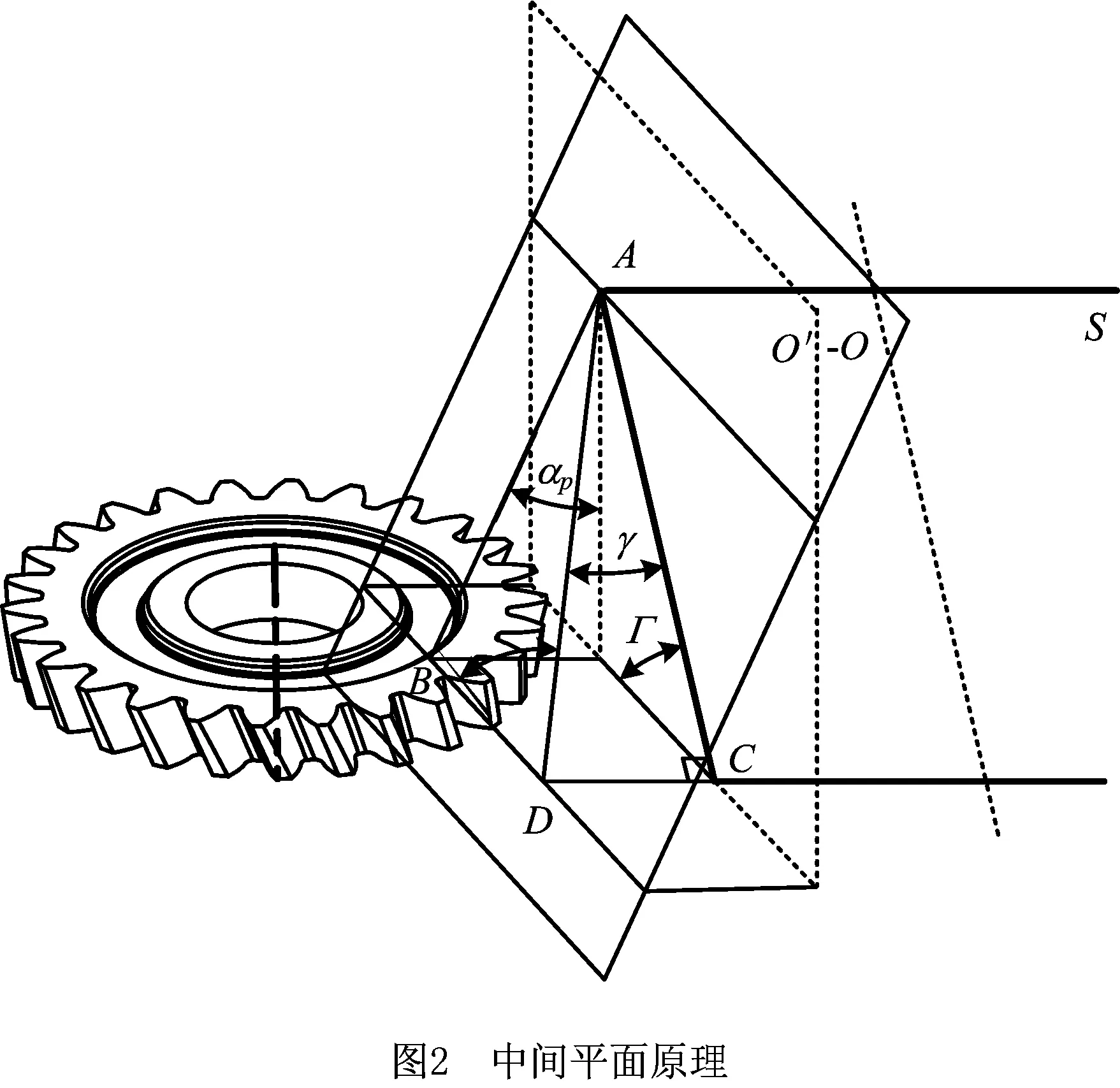
图2中，锥角γ与变厚齿轮的安装角Γ、轴向后角αp的关系为

tanγ=sinΓtanαp。

(4)

安装角的计算公式为

Γ=±(90-βs)∓βc。

(5)

式中：βc，βs分别为变厚齿轮与砂轮的螺旋角；第1个“±”的上面(下面)与蜗杆砂轮的左旋(右旋)对应，第2个“∓”的上面(下面)表示变厚齿轮与蜗杆砂轮的螺旋线具有相同(相反)方向。

结合式(4)和式(5)可知，根据βs的选取，有安装角为0的情况，此时锥形蜗杆砂轮的锥角γ=0，即为圆柱蜗杆砂轮，因此可将圆柱蜗杆砂轮看作锥形蜗杆砂轮在γ=0时的一个特殊情况。

1.3 电子齿轮箱联动模型

实际加工时根据各机床轴间的空间位置关系及齿轮啮合需求，需要推导出各主动轴与随动轴间的联动比关系式，电子齿轮箱模型的建立原则是刀具和工件相对位置随着齿轮的变位系数变化。图3所示为机床示意图。蜗杆砂轮与齿轮之间为连续展成运动，展成运动(同步轴)包括蜗杆砂轮的径向进给运动(X轴)、蜗杆砂轮的旋转运动(B轴)、沿工件切向运动(Y轴)、沿工件轴向运动(Z轴)、工件的回转运动(C轴)。

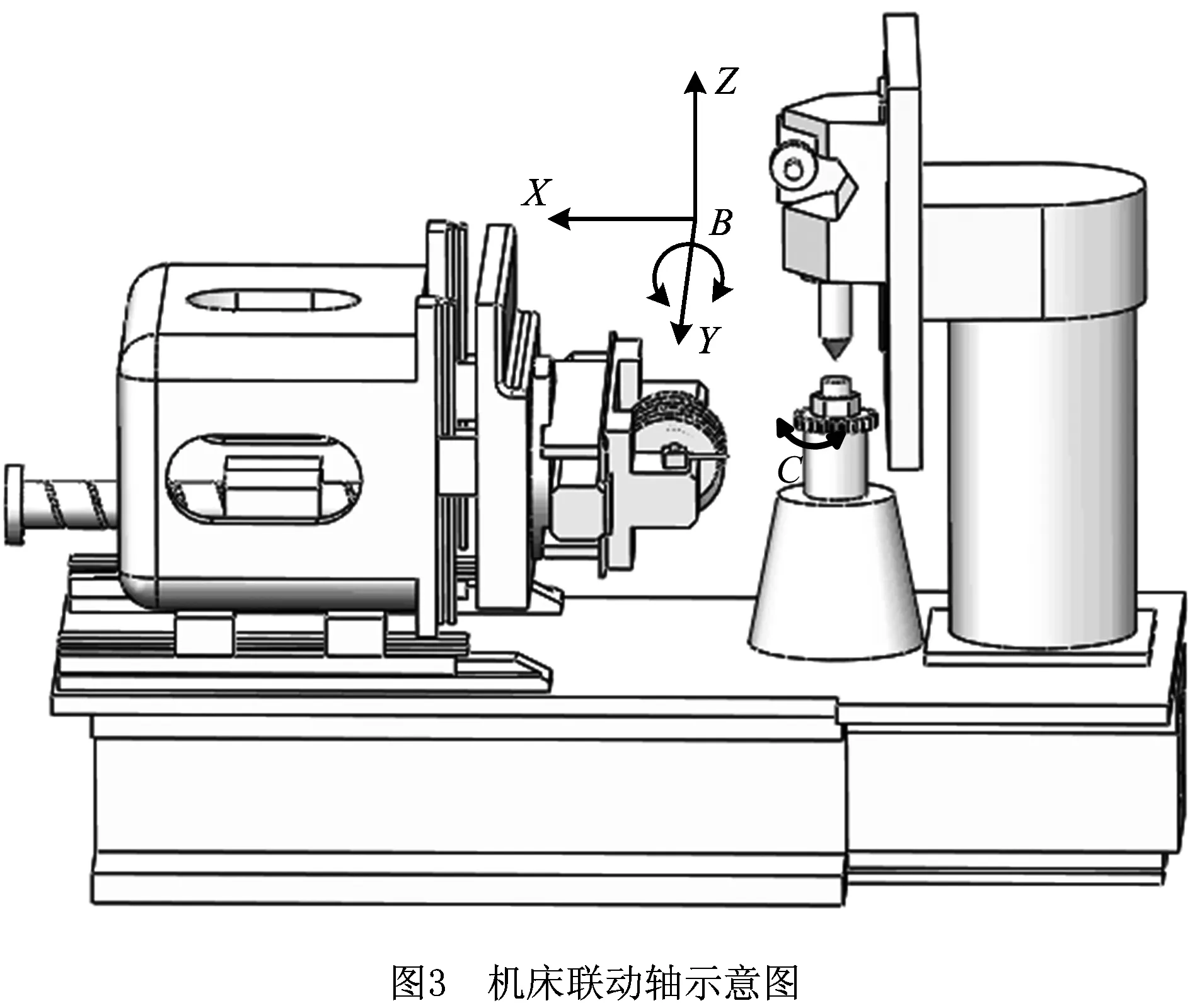
展成运动通过电子齿轮箱实现，电子齿轮箱中的运动轴称为同步轴，同步轴又分为主动轴和随动轴，其中随动轴只能有一个，主动轴可以为多个，主动轴为程序控制，随动轴为跟随控制。根据需求在电子齿轮箱中建立两个联动模型，第1个为展成加工联动模型，Y，Z，B轴为主动轴，C轴为随动轴；第2个为蜗杆砂轮窜刀联动模型，Y，Z轴为主动轴，X轴为随动轴。

(1)展成加工联动模型

(6)

式中：βs为蜗杆砂轮螺旋角；βc为变厚齿轮螺旋角；ds为蜗杆砂轮分度圆直径平均值；dc为变厚齿轮分度圆直径；zs为蜗杆砂轮头数；zc为变厚齿轮齿数。

(2)砂轮窜刀联动模型

(7)

2 锥形蜗杆砂轮的几何参数计算

2.1 齿形角与导程

锥形蜗杆砂轮的主要参数都可以根据产形齿条求出，现以齿形角和导程为例。图4所示为锥形蜗杆砂轮数学模型建立的流程。过直线AD的蜗杆砂轮轴截面如图4c所示，图中的虚线圆表示锥形蜗杆加工中的不同半径变厚齿轮圆截面，图4a和图4b为变厚齿轮对应的产形齿条。

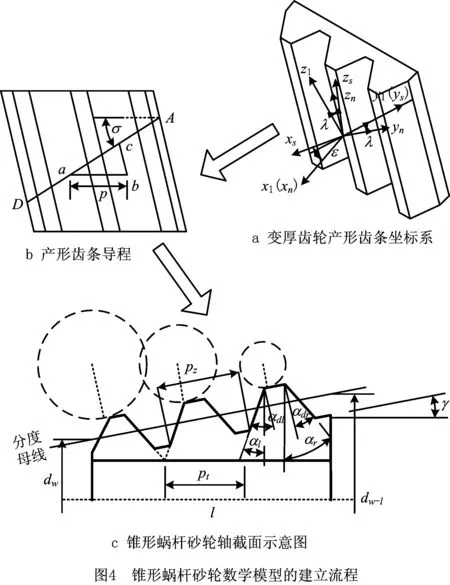
如图4所示，在产形齿条中建立坐标系Sn，xn垂直于产形齿条分度面O，zn平行于螺旋线，(xn,yn)平面即为产形齿条法平面。将yn，zn旋转λ角度(λ为砂轮的展成角)建立过渡坐标系S1，x1与xn共线，y1，z1分别与yn，zn的夹角为λ。设ε为产形齿条分度面O与轴截面S的夹角的余角，将x1，z1绕y1轴旋转ε角度即为固结于蜗杆砂轮的坐标系Ss，平面(xs,ys)为轴截面S，zs垂直于轴截面S。其中

ε=90°-arccos

(8)

图中坐标系Sn与S1、S1与Ss的变换矩阵为：

(9)

式中：M1n表示坐标系Sn变换到S1中的矩阵，Ms1表示坐标系S1变换到Ss中的矩阵。则坐标系Sn变换到坐标系Ss中的矩阵

Msn=Ms1·M1n=

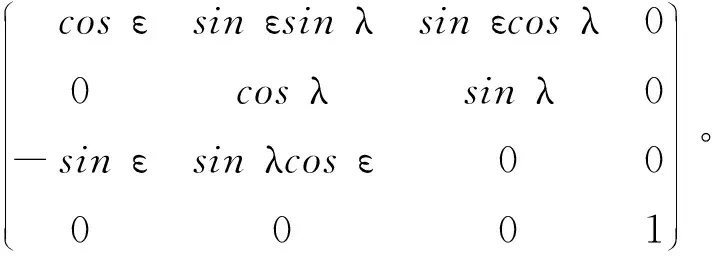
(10)

坐标系Sn中产形齿条左右齿廓的法向量分别表示为：

nnl=(sinαn,-cosαn,0)；

nnr=(sinαn,cosαn,0)。

(11)

将该齿廓法向量表示在Ss坐标系中：

nl/r=Msn·nnl/nr。

(12)

该轴截面S在产形齿条中截出的廓形属于Ss坐标系(xs,ys)平面，垂直于Ss坐标系的zs轴，且垂直于齿廓法向量nl/r。则齿廓的方向向量

al/r=nl/r×(0,0,1)。

(13)

设αd(l/r)为轴截面上剖出的锥向齿廓齿形角，通过上面计算求得其值为：

(14)

(15)

图4中，αl/r，表示轴截面上轴向齿形角，

αl=αdl-γ，αr=αdr+γ；

(16)

pz，pt为蜗杆的锥向导程和轴向导程。实际生产中，为了简化锥形蜗杆模型，亦便于进行修整和磨削加工，取蜗杆砂轮的导程为固定值，并与产形齿条的导程p有如下关系式：

(17)

锥形蜗杆砂轮不同端截面的分度圆直径是渐变的，锥形蜗杆砂轮的螺旋角βs随分度圆直径变化，经计算，其变化量很小，可选择蜗杆分度圆直径的平均值ds近似计算：

(18)

式中：mn为法向模数，zs为蜗杆砂轮头数。锥形蜗杆砂轮的螺旋角确定之后，安装角和导程通过计算可以确定。又因为安装角和导程之间有关系，为了确定三者的值，采用迭代的方法求出最优解，实际中求出的值差值很小,可忽略。针对蜗杆砂轮类型，应尽可能选取头数较少的蜗杆砂轮，可最大程度地减小由蜗杆砂轮锥度引起的螺旋角误差及轴向导程误差。

2.2 锥形蜗杆砂轮齿面建模

实际的锥形蜗杆砂轮齿面由其修整方法确定。砂轮左右齿面沿轴向齿形角不相等，因此采用金刚滚轮单面修整方法。修整砂轮的锥面金刚滚轮的齿形角为固定值，为保证修整出满足要求的锥形蜗杆齿形角，需调整滚轮在水平截面内的姿态。在修整锥形蜗杆砂轮过程中，为简化运动模型，假定修整过程中滚轮静止，滚轮沿砂轮的中心线进行定导程螺旋线运动。此外，蜗杆砂轮径向进给轴X与轴向运动轴Y之间还需联动以实现砂轮锥形修整，X轴与Y轴的联动比为

X=tanγY。

(19)

其中，联动比的正负与机床轴X，Y的方向及砂轮锥度方向有关。

基于包络原理，在滚轮与锥形蜗杆砂轮间运动关系确定的前提下，锥形蜗杆砂轮的齿面由滚轮锥面包络而成。设St是固接于滚轮的坐标系，机床固定坐标系为So。以右旋锥形蜗杆砂轮为例，金刚滚轮的右侧产形锥面如图5所示，图中：θt为滚轮的转角，μt确定锥面上的点在圆锥母线上的位置，Lt为锥面顶点在轴线上的位置，αdr为右侧锥面齿形角。

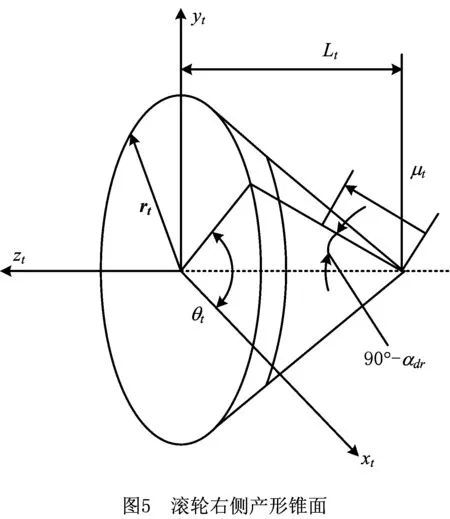
滚轮右侧产形锥面族的向量表示为

(20)

圆锥面的单位法线矢量为

(21)

设滚轮的转速为ωt，则滚轮与蜗杆砂轮间的相对速度

(22)

式中向量Rt表示蜗杆砂轮坐标原点Os在滚轮坐标系St中的位置矢量。滚轮锥面与蜗杆砂轮齿面为一对共轭齿面，在接触点处一定满足啮合方程式

(23)

将滚轮产形锥面族表达式进行坐标变换得到

rs(μt,θt,ψ)=MtoMosrt(μt,θt)。

(24)

式中：rs(μt,θt,ψ)表示在蜗杆砂轮坐标系Ss中的锥面族表达式，ψ表示蜗杆的旋转角；Mto，Mos分别表示机床坐标系与滚轮坐标系、蜗杆坐标系与机床坐标系间的变换矩阵。

运用解析计算法联立式(23)和式(24)，可求得滚轮与锥形蜗杆砂轮的接触线，将接触线绕蜗杆砂轮轴线螺旋投影即得锥形蜗杆砂轮的曲面方程。将式(20)代入式(23)，推导出参数μt与θt间的关系:

μt=Lt/sinαdr-tanθt(asinαdrcotλ+ptsinαdr)-

(25)

锥形蜗杆砂轮理论齿形面表达式如下：

(26)

(27)

式中：F_l，F_r分别表示左右齿面的齿面方程，D为蜗杆砂轮大端最外缘直径。

3 锥形蜗杆砂轮磨削的数字仿真分析

3.1 锥形蜗杆砂轮数字包络仿真

为了验证锥形蜗杆砂轮包络变厚齿面方法的准确性和有效性，利用软件采用数字方法进行包络仿真。考虑到理论建模的精度，采用数字仿真方法对锥形蜗杆砂轮的齿面进行理论建模，根据啮合原理求出砂轮与齿轮的接触迹，接触迹投影到平面上即为变厚齿轮的廓形，对齿廓廓形的误差进行量化分析，从而对文中提出的磨削工艺进行验证。

以某一斜变厚齿轮包络仿真为例进行仿真模拟，其齿轮相关参数如表1所示。

表1 变厚齿轮基本参数

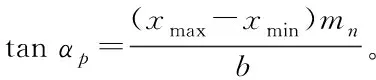
根据齿轮参数计算蜗杆砂轮的几何参数，并确定刀具和工件的相对位置。通过计算坐标系中X，Z方向的中心距，确定啮合的相对位置，起始中心距计算为：

Ex=rc+rscosαp;

(28)

Ez=rrsinαp。

(29)

式中：rs为锥形蜗杆当前接触面的分度圆半径，rc为变厚齿轮节圆半径。

数值模拟时，蜗杆砂轮可以不做冲程轨迹运动，只需求得当前相对位置的接触迹，接触迹经过螺旋投影即得被包络齿面的端面廓形。

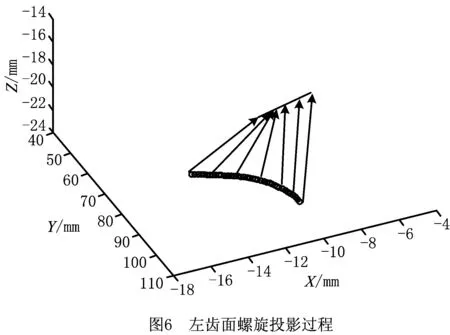
在MATLAB软件同一坐标系中分别描述出锥形蜗杆砂轮的左、右齿面，利用啮合原理对齿面求导解其法向量，根据啮合点法向量和相对速度在接触点乘积等于0的关系，可以求出共轭面的啮合接触迹[16]。在展成运动仿真过程中，齿轮每次运动旋转单位角度，砂轮也进行相应的运动，最后与齿轮啮合，得到一系列离散的啮合接触点，通过计算得到一系列点表示的共轭面接触迹，将其光滑连接即为完整的接触迹。图6和图7所示为螺旋角不为0°时，齿轮坐标系中左右齿面的接触迹，由于左右齿面的螺旋角不一样，其接触迹需分别计算。图中表示了将接触迹投影到z=-21 mm平面上的过程，所得廓形如图6和图7所示。图6为左齿面的投影过程，将每次啮合的接触点光滑连接即为左齿面接触迹，所得的啮合点从齿顶到齿底越来越密集，其中实线连接的点为将接触迹投影到z=-21 mm平面上所得的左廓形，箭头表示螺旋投影过程；图7为右齿面的投影过程，同理将接触啮合点光滑连接即为右齿面接触迹，同样所得的啮合点从齿顶到齿底越来越密集，其中实线连接的点为将接触迹投影到z=-21 mm平面上所得的右廓形，箭头表示螺旋投影过程。

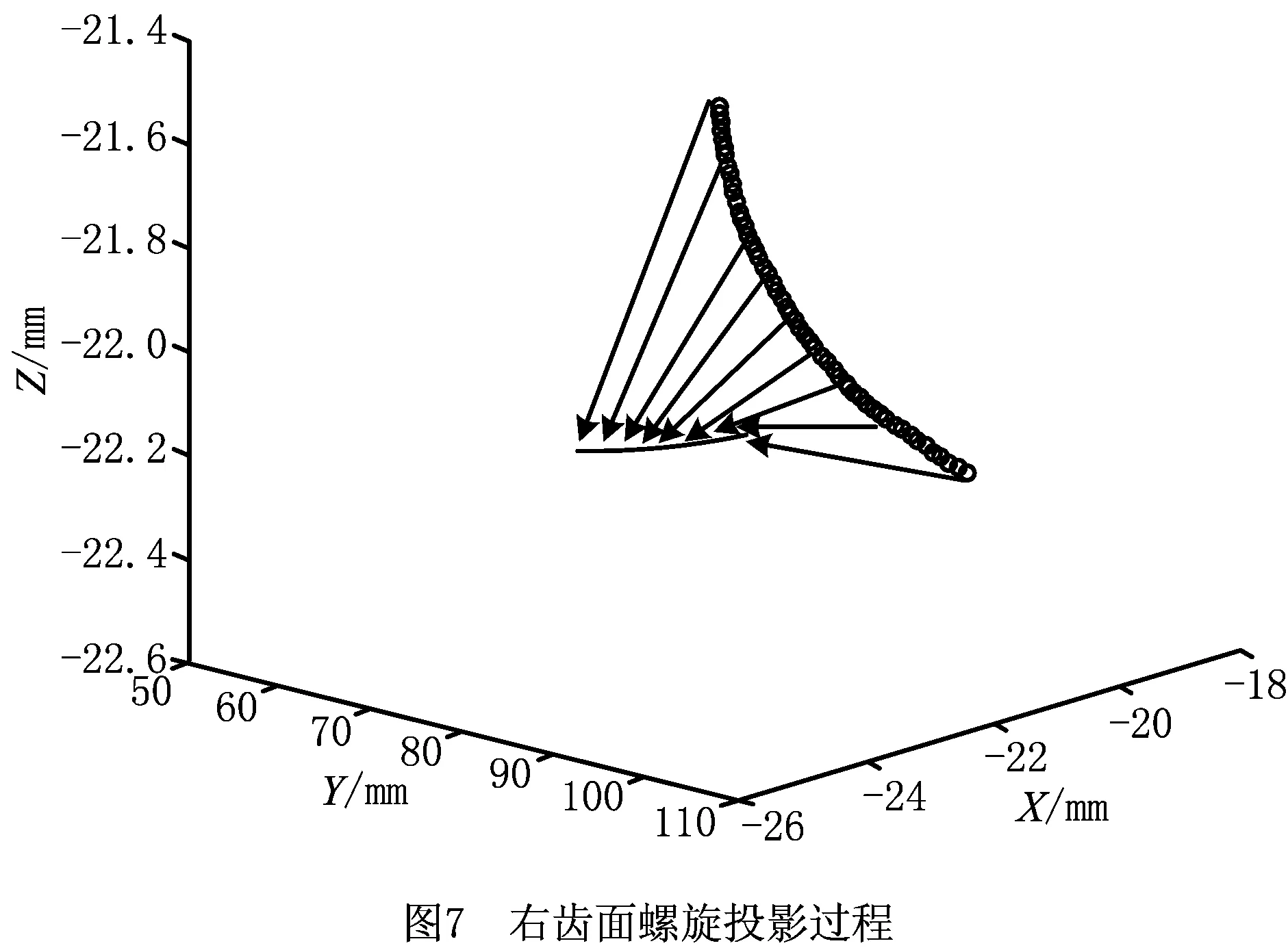
变厚齿轮的左右齿面接触迹在同一坐标系的空间位置有较大差异，螺旋投影的角度也不一样，但都投影到相同平面上得到一个完整齿的廓形，廓形由一系列点表示。

3.2 变厚齿轮锥面砂轮磨削精度分析

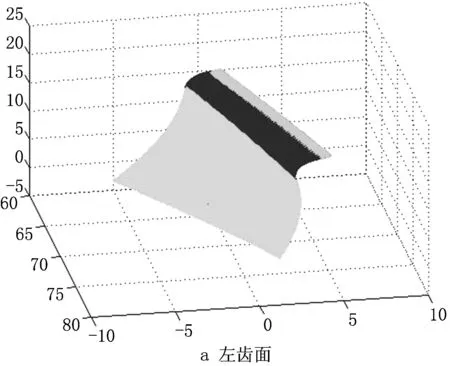
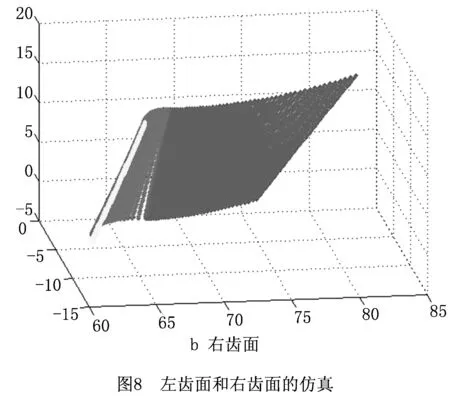
磨削出的变厚齿轮截面廓形误差是齿轮精度的重要验证指标。为获得仿真加工的变厚齿轮廓形的精度，需要建立变厚齿轮相应的理论三维模型。首先根据产形齿条包络原理，利用MATLAB计算出单齿的左右齿面(如图8)，左右齿面分别由渐开线区域、过渡区域、圆弧区域组成，然后将生成的齿面导入三维软件，再经过阵列、缝合等手段得到变厚齿轮的理论模型[17]。

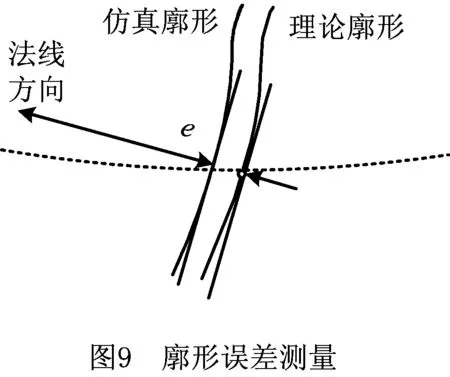
因为虚拟三维齿轮不能用齿轮仪实际测量，所以取变厚齿轮的理论标准齿面与仿真加工齿面对应的轴截面廓形进行对比。首先选择理论标准廓形上的一点，并取过该点渐开线的公法线，公法线方向标准廓形点到仿真廓形对应点的位置代数差e即为该点的齿廓误差，齿厚变小时e为负值，齿厚变大时e为正值，如图9所示。

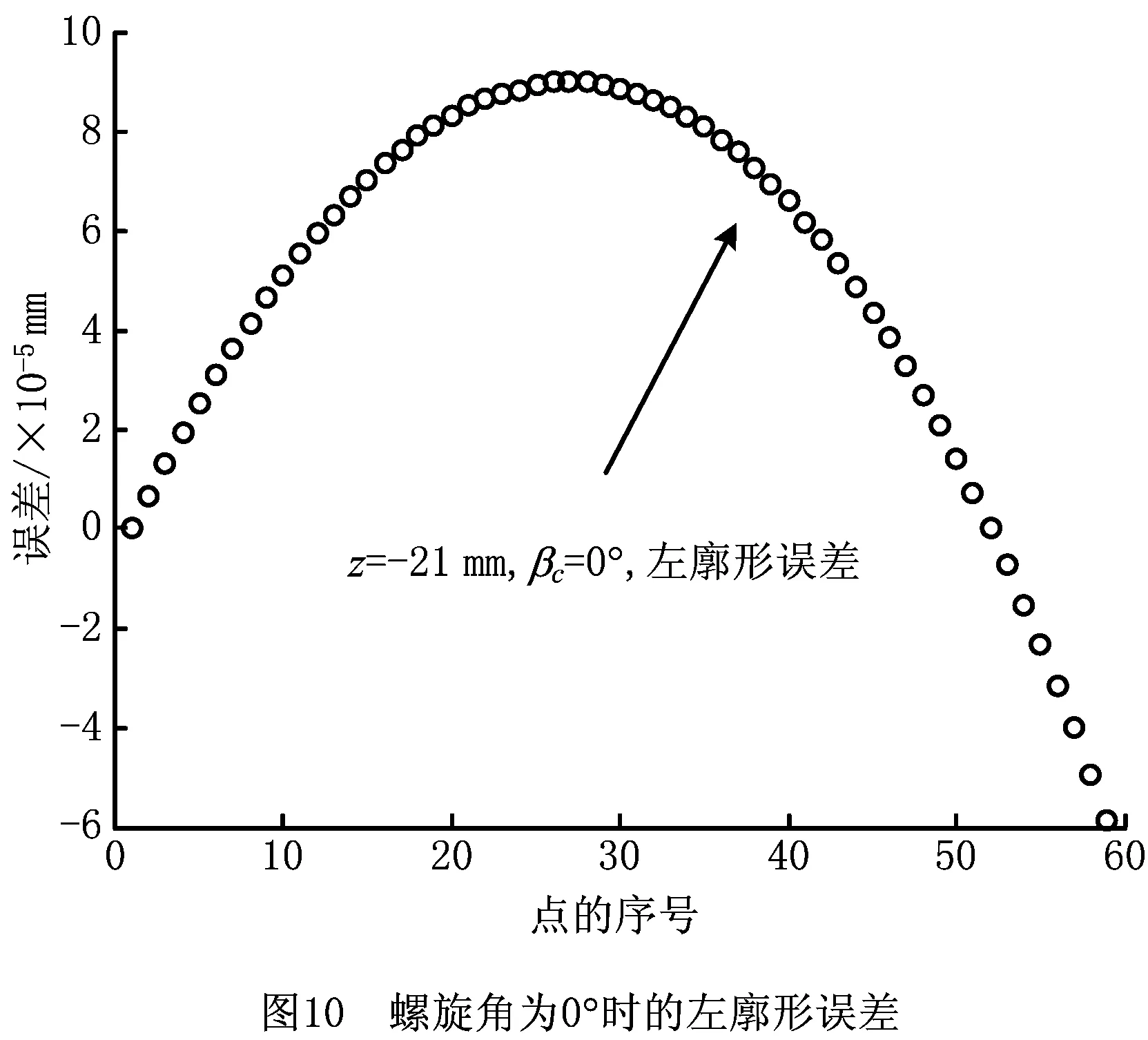
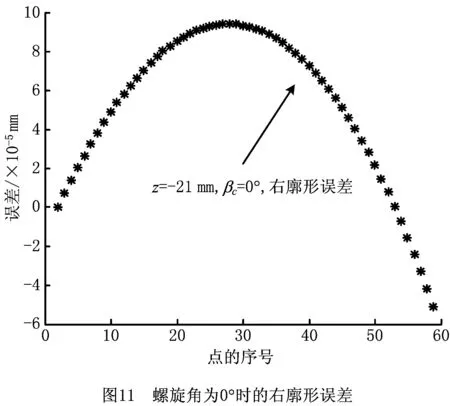
将仿真结果与标准廓形同位置的点做误差对比，并分别对直齿和斜齿时的情况进行分析。图10和图11所示为螺旋角βc=0°时的齿面左右廓形误差。左右齿面投影得到的廓形点分别为60个，序号0～60的点位置依次从齿底到齿顶变化。可知，当螺旋角为0°时，采用该工艺磨削左右廓形误差绝对值均不超过0.000 1 mm，直齿的情况完全满足加工要求。

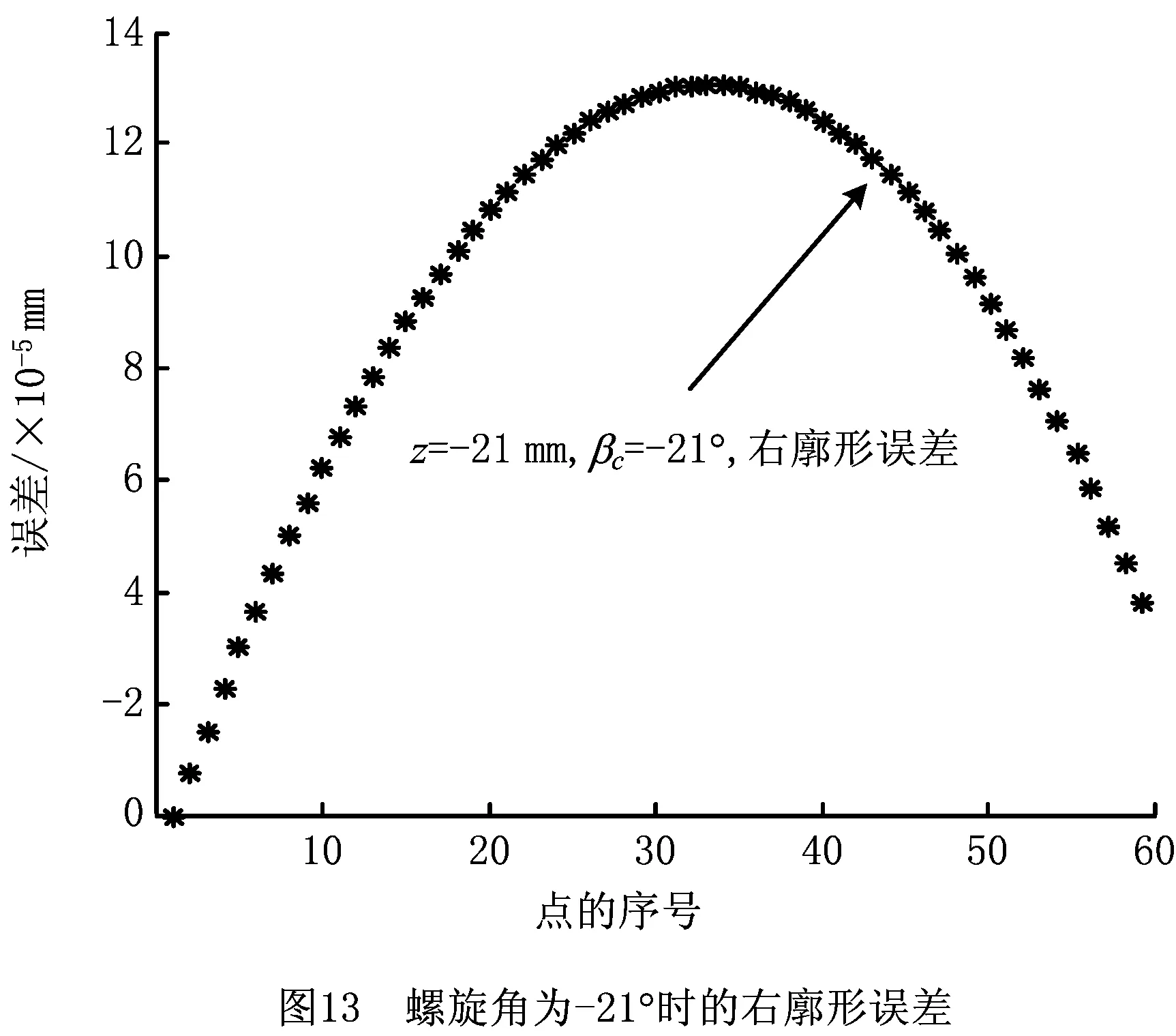
当斜齿螺旋角βc=-21°时，廓形误差如图12和图13所示。可知，随着螺旋角的产生，最大廓形误差相应增大。齿顶的廓形误差变化较大，当螺旋角大到一定程度时，误差曲线不再是抛物线，而是近似为直线，但其误差仍保持在±0.001 mm以内。斜齿时，因为左右齿面螺旋角不一样，所以两齿面的齿形误差大小并不相等。

无论变厚齿轮为直齿还是斜齿，相比较传统工艺，锥型蜗杆砂轮工艺都能磨削更高精度的齿面，完全满足市场的要求。目前，该方法的问题是螺旋角不为0°时，磨削齿形会产生更大误差。根据廓形误差的曲线图可以看出，误差呈抛物线变化，在分度圆与廓形相交点处的廓形误差达到最大，可以推断此处是由压力角误差引起的主要廓形误差，因此可以根据实际情况进行压力角修正以提高精度。

4 结束语

本文针对变厚齿轮的高效精密磨削进行研究，提出了变厚齿轮的锥形蜗杆砂轮磨削方法，其主要工作如下：

(1)分析了变厚齿轮的几何特点，提出变厚齿轮的锥形蜗杆砂轮磨削工艺，建立了蜗杆砂轮锥形数学模型，并给出了砂轮磨削时的电子齿轮箱联动模型。

(2)推导了锥形蜗杆砂轮的主要参数计算公式，给出锥形蜗杆砂轮的修整方法，最后给出锥形蜗杆砂轮齿面的方程表达式。

(3)对锥形蜗杆砂轮包络齿轮过程进行了数字模拟仿真，计算了包络时齿面上的接触迹，将其螺旋投影到平面获得齿轮截面廓形。最后与齿轮标准廓形比较，获得廓形误差曲线图，验证了锥形蜗杆砂轮磨削变厚齿轮齿面方法的准确性。

(4)通过分析磨削原理和结果误差可知变厚齿轮的锥形蜗杆砂轮磨削新工艺具有重合度大、啮合线长、干涉小等特点，磨削过程类似于普通的圆柱蜗杆砂轮磨，其能同时加工左、右齿面。相比于大平面磨削，该工艺为连续展成磨削，效率高；相比于圆柱蜗杆砂轮磨，该工艺提高了变厚齿轮的加工精度。因此，该新工艺具有高效高精的优点。

下一步将把本文建立的模型集成到项目组参与开发的YW7232CNC蜗杆砂轮磨齿机中，通过实际加工进一步完善该工艺。

参考文献:

[1] TRONG P D, PASCAL Z, PETER E. Review on contact simulation of beveloid and cycloid gears and application of a modern approach to treat deformations[J]. Mathematical and Computer Modeling of Dynamical Systems,2015,21(4):359-388.

[2] MITOME K I. Table sliding taper hobbing of conical gear using cylindrical hob. Part1:theoretical analysis of table sliding taper hobbing[J]. Transactions of the ASME,1981,103(4):452-456.

[3] MITOME K I. Infeed Grinding of straight conical involute gear[J].Japan Society of Mechanical Engineers International Journal，1993,36(543):3656-3661.

[4] HE Jingliang, WU Xutang. On the hobbing principle of conical involute gears[J]. Mechanical Science and Technology for Aerospace Engineering,2003,22(5):751-753(in Chinese).[贺敬良,吴序堂.渐开线锥形齿轮滚削原理[J].机械科学与技术,2003,22(5):751-753.]

[5] HE Jingliang, WU Xutang. The grinding principle of conical involute gears on NC conical wheel gear grinding machine[J]. Heavy Machinery,2003(3):15-18(in Chinese).[贺敬良,吴序堂.数控锥面砂轮磨齿机磨削锥形齿轮原理[J].重型机械,2003(3):15-18.]

[6] WANG Guangjian, CHU Zhigang. Research on the modification coefficient calculation of conical involute planetary gear with few tooth difference[J].China Mechanical Engineering,2009,20(4):481-484(in Chinese).[王光建,褚志刚.变齿厚齿轮少齿差传动变位系数计算研究[J].中国机械工程,2009,20(4):481-484.]

[7] BRECHER C, BRUMM M, HÜBNER F, et al. Influence of the manufacturing method on the running behavior of beveloid gears[J]. Production Engineering,2013,7(2):265-274.

[8] BRECHER C, LÖPENHAUS C, GRESCHERT R. Influence of the metal working fluid on the running behavior of gear analogy test parts[J]. Production Engineering,2015,9(3):425-431.

[9] BRECHER C, LÖPENHAUS C, BRIMMERS J. Function-oriented tolerancing of tooth flank modifications of beveloid gears[J]. Procedia Cirp,2016,43:124-129.

[10] HUANG Jinli. Research on machining method of space beveloid gear pairs[D]. Harbin:Joural of Harbin Engineering University,2014(in Chinese).[黄金利.空间变厚齿轮副加工方法的研究[D].哈尔滨:哈尔滨工业大学,2014.]

[11] ZIMMER M, OTTO M, STAHL K. Homogeneous geometry calculation of arbitrary tooth shapes-mathesmatical approach and practical applications[C]//Proceedings of American Gear Manufacturers Association Fall Technical Meeting. New York, N.Y., USA: Curran Associates, Inc, 2015: 196-212.

[12] ZHU Caichao, LIU Libin, LIU Mingyong, et al. Geometry design and tooth contact analysis of intersected beveloid gears[J]. Journal of Mechanical Engineering,2012，48(23):135-142(in Chinese).[朱才朝,刘立斌,刘明勇，等.相交轴渐开线变厚齿轮几何设计与啮合特性分析[J].机械工程学报,2012，48(23):135-142.]

[13] NI Gaoxiang, ZHU Caichao, SONG Chaosheng, et al. Geametric design and meshing characteristics analysis of beveloid gear transmission with parallel axes [J]. Journal of Xi’an Jiaotong University, 2016,50(5): 57-64(in Chinese). [倪高翔,朱才朝,宋朝省,等.平行轴渐开线变厚齿轮传动的几何设计与啮合特性分析[J].西安交通大学学报,2016,50(5):57-64.]

[14] NI Gaoxiang, ZHU Caichao, SONG Chaosheng, et al. Tooth contact analysis of crossed beveloid gear transmission with parabolic modification[J]. Mechanism & Machine Theory,2017,113:40-52.DOI:10.1016/J.mechmachtheory.2017.03.004.

[15] AMANI A, SPITAS C, SPITAS V. Generalised non-dimensional multi-parametric involute spur gear design model considering manufacturability and geometrical compatibility[J]. Mechanism & Machine Theory,2017,109:250-277.

[16] LITVIN F L. Gear geometry and applied theory[M]. Shanghai:Shanghai Science and Technology Press，2008(in Chinese).[F.L.李特文.齿轮几何学与应用理论[M].上海：上海科学技术出版社,2008.]

[17] LIN Chao, WEI Peitang, ZHU Caichao, et al. Study on the tooth surface generation of helical beveloid gear[J].Journal of Mechanical Transmission,2010,34(4):1-5(in Chinese).[林 超,魏沛堂,朱才朝,等.变齿厚斜齿轮的齿面生成研究[J].机械传动,2010,34(4):1-5.]