基于改进田口试验法的装配公差分析

陈志英，刘 勇，周 平，刘广通

(北京航空航天大学 能源与动力工程学院，北京 100191)

0 引言

航空发动机的研制过程具有精度高、装配结构复杂、计算量大、研制周期短等特点和要求[1]，装配过程为实现发动机功能的重要环节，零部件的几何尺寸和公差信息是保证发动机装配成功率的关键，也会影响发动机的研制周期和研制成本。因此，针对航空发动机的公差分析方法不但要保证其功能、性能和可装配性的要求，而且要求在保证封闭环公差的前提下具备较高的计算精度和效率。

现有的公差分析方法包括极值法和统计法[2-3]。极值法只考虑装配中各部件尺寸的最大值与最小值[4]，忽略了实际尺寸在其公差范围内的分布情况，得出的结果往往过于极端，并且增加了制造成本。在现代大规模的生产活动中，机械产品每一个零件的尺寸X1,X2,…,Xi,…,XN(1≤i≤N)通常被看作是一个随机变量，且服从某一特定类型的分布。在装配过程中，封闭环的几何尺寸Y是各个组成环几何尺寸的函数，即Y=F(X1,X2,…,Xi,…,XN)，组成环尺寸的变动会直接影响封闭环的尺寸，并且各个组成环的尺寸误差会累计形成累积误差，进而影响产品的性能，因此封闭环的尺寸是一个随机变量，应服从某一类型的分布[5]，统计法正是基于这样的认识而提出的一种公差分析方法。统计公差分析方法主要有均方根法、蒙特卡洛法、田口试验法和卷积法[6]。均方根法虽然考虑了部件尺寸的分布情况，但是其假设过于理想，即各部件在公差范围内服从正态分布，并且名义值和平均值重合，这种假设在实际情况中很难出现。基于蒙特卡洛法的公差分析方法适用于部件尺寸为非正态分布的情况，并且随着计算次数的增加，计算精度也会提高，但是蒙特卡洛法需要大量的计算样本，因此计算时间长，效率低[7-9]。卷积法虽然也能够处理尺寸为非正态分布的情况，但是计算过程复杂，计算工作量大[10-11]。田口试验法由于计算过程简单、易于理解，已被广泛应用于工业界[12]，钱泽鹏等[13]基于田口试验法对某工件进行了公差分析，并在此基础上进行了公差尺寸链的优化设计；Feng等[14]以公差累积的变动最小为目标，基于田口试验法对某轴组件进行了公差分析和设计；Muthu等[15]基于田口试验法，结合启发式算法对超越离合器进行了公差分析和优化设计。然而，田口试验法只适用于部件尺寸为正态分布的情况，田口玄一博士也未在其著作中就田口试验法的理论基础给出说明[16-17]，而且传统的田口方法只能准确估计统计量的前两阶矩，对三阶、四阶矩估计的精度欠佳。

目前，装配成功率的计算方法主要有矩估计法(二阶矩、四阶矩)和蒙特卡洛法等[18]，二阶矩法能够准确估计统计量的前两阶矩，然而前两阶矩并不能准确反映统计量的分布类型，因此得出的装配成功率在精度上不够高；蒙特卡洛法则在对数据处理的效率上明显低于矩估计法。

综上所述，基于传统的田口试验法，本文提出一种改进的试验设计方法，并就其理论基础给出了完整的推导过程，该方法不但适用于组成环尺寸为正态分布的情况，而且适用于尺寸分布为非正态的情况。另外，该方法可以比较准确地估算统计量的前四阶矩，并结合Pearson分布理论，较准确地得到装配成功率的值，从而在保证计算精度的前提下减小计算量，提高装配公差分析效率。将该方法应用于某型航空发动机涡轮转子的径向装配尺寸链中，能够为航空发动机的装配成功率提供新的检验方法。

1 改进的田口试验法

田口试验法的理论基础是高斯数值积分[19]，具有n个节点的高斯数值积分公式为

(1)

式中：ρ(x)为积分区间[a,b]上的权重函数，φ(x)为被积函数，ωi和xi为与被积函数φ(x)无关的权重因子和积分节点。合理地选择积分节点x1,x2,…,xn，可使积分公式对次数小于等于2n-1的多项式精确成立，即式(1)的代数精度为2n-1[20]。

响应函数g(x)的k阶原点矩

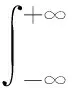
(2)

式中f(x)为随机变量x的概率密度函数，x的均值和方差分别为μ,σ。

令[g(x)]k=φ(x)为被积函数，f(x)=ρ(x)为权重函数，选取xi=μ+αiσ为积分节点，根据式(1)，将式(2)表示为

E(gk)≈ω1[g(μ+α1σ)]k+ω2[g(μ+α2σ)]k

+…+ωn[g(μ+αnσ)]k。

(3)

对于三水平的试验设计来说，其积分节点数n=3(代数精度为5)，则式(3)变为

E(gk)≈ω1[g(μ+α1σ)]k+ω2[g(μ+α2σ)]k+

ω3[g(μ+α3σ)]k。

(4)

根据Engels[21]的结论可知，式(4)中的参数{ω1,ω2,ω3,α1,α2,α3}可通过随机变量x的前k阶中心矩进行求解。已知xi=μ+αiσ为积分节点，将积分节点xi取为各因素的三个水平li，即令

li=xi=μ+αiσ，i=1,2,3，

(5)

从而将求解{ω1,ω2,ω3,α1,α2,α3}变为求解{ω1,ω2,ω3,l1,l2,l3}。

各个因素的k阶中心矩表示为

ω2(α2σ)k+ω3(α3σ)k

=ω1(l1-μ)k+ω2(l2-μ)k+ω3(l3-μ)k。

(6)

当k分别取1，2，3，4时，可得前四阶中心矩：

m1=ω1(l1-μ)+ω2(l2-μ)+ω3(l3-μ);

(7)

m2=ω1(l1-μ)2+ω2(l2-μ)2+ω3(l3-μ)2;

(8)

m3=ω1(l1-μ)3+ω2(l2-μ)3+ω3(l3-μ)3;

(9)

m4=ω1(l1-μ)4+ω2(l2-μ)4+ω3(l3-μ)4。

(10)

各因素的均值、方差、偏度、峰度与前四阶中心矩的关系为：

μ=m1;

(11)

σ2=m2;

(12)

(13)

β2=m4/(m2)2。

(14)

在因素分布类型已知的前提下，可求得：

m1=μL;

(15)

m2=σ2;

(16)

(17)

m4=β2σ4。

(18)

因此式(7)～式(10)变为：

ω1(l1-μ)+ω2(l2-μ)+ω3(l3-μ)=μ;

(19)

ω1(l1-μ)2+ω2(l2-μ)2+ω3(l3-μ)2=σ2;

(20)

(21)

ω1(l1-μ)4+ω2(l2-μ)4+ω3(l3-μ)4=β2σ4。

(22)

权重之和为1，即

ω1+ω2+ω3=1，

则

ω2=1-ω1-ω3。

(23)

根据田口试验方法，令因素的中间水平

l2=μ。

(24)

将式(23)和式(24)代入式(19)～式(22)，有：

ω1(l1-μ)+ω3(l3-μ)=μ;

(25)

ω1(l1-μ)2+ω3(l3-μ)2=σ2;

(26)

(27)

ω1(l1-μ)4+ω3(l3-μ)4=β2σ4。

(28)

解式(25)～式(28)得：

(29)

(30)

(31)

(32)

将ω1，ω3代入式(23)，得

(33)

其中，均值、标准差、偏度和峰度可通过下式计算：

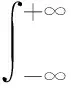
(34)

(35)

(36)

(37)

另外已知l2=μ，至此可求出每个因素的3个水平值以及各自的权重因子，则响应函数的均值、标准差、偏度和峰度为：

(38)

(39)

(40)

2 Pearson分布理论及装配成功率估算方法

2.1 Pearson分布理论

基于蒙特卡洛模拟方法的基本原理，Karl Pearson提出一种包括多种分布类型的统一模型[22]

(42)

式中：p(x)为概率密度函数；a，c0，c1，c2为分布参数，是概率密度函数的前四阶矩的函数。因此只要得到样本的前四阶矩，便可根据Pearson微分方程(42)解得概率密度函数，而且根据不同的参数取值可以得到不同的概率密度函数。由Pearson分布模型建立的分布族如表1所示。

表1 Pearson分布族

由表1可以看出，Pearson分布包含了任意给定均值、标准差、偏度和峰度的常见分布类型，如正态分布、β分布、γ分布、t分布等。

得到响应函数的均值、标准差、偏度和峰度后，根据Pearson分布族理论，即可确定响应函数的分布类型及概率密度函数。

2.2 装配成功率估算方法

装配成功率指封闭环的尺寸变量Y落在公差允许的区间R0内的概率[1,18]。设封闭环的概率密度函数为f(Y)，则装配成功率

若采用蒙特卡洛法估算装配成功率，则

式中：N0为由组成环样本计算得到的封闭环尺寸落在R0内的个数，Ntotal为总的模拟次数。

3 实例分析

如图1所示，δ为高压一级涡轮叶尖与机匣的间隙，L1为机匣内径，L2为叶尖到涡轮盘外沿长度，L3为涡轮盘半径。要求叶尖间隙δ符合2.8 mm≤δ≤3.2 mm，为装配成功。各组成环的尺寸参数如表2所示。

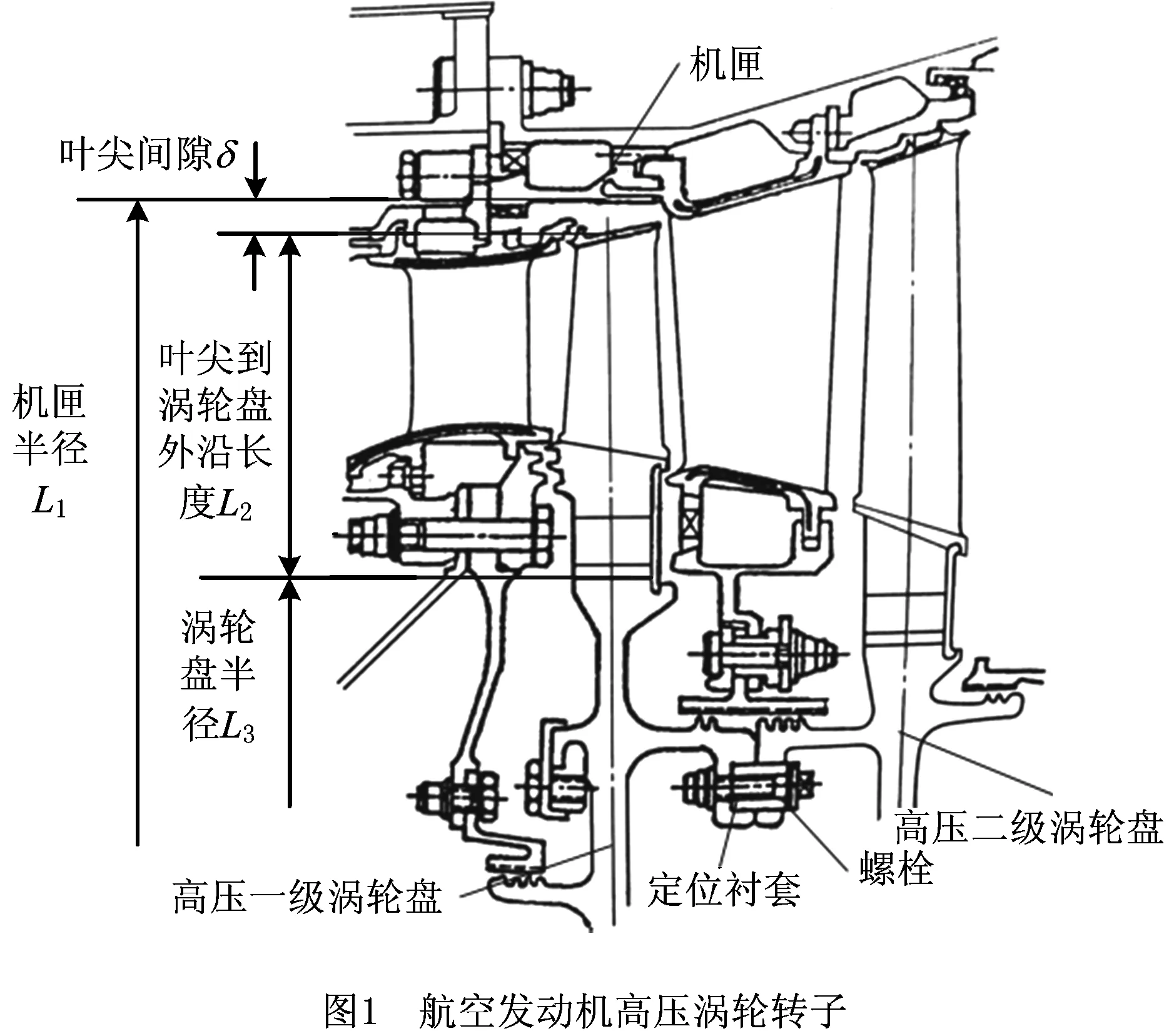
表2 组成环尺寸参数

组成环L1L2L3公称尺寸/mm672.5311.0358.5公差/mm0.30.20.2传递比ξi=∂f/∂Li1-1-1

3.1 装配公差分析

由图1可以确定，组成环L1为增环，L2，L3为减环，则封闭环

(45)

在机械加工过程中，部件的常见分布类型有正态分布、β分布、均匀分布等，假设组成环的尺寸符合这几种类型的分布，本文设计了4种不同分布类型的组合，如表3所示。

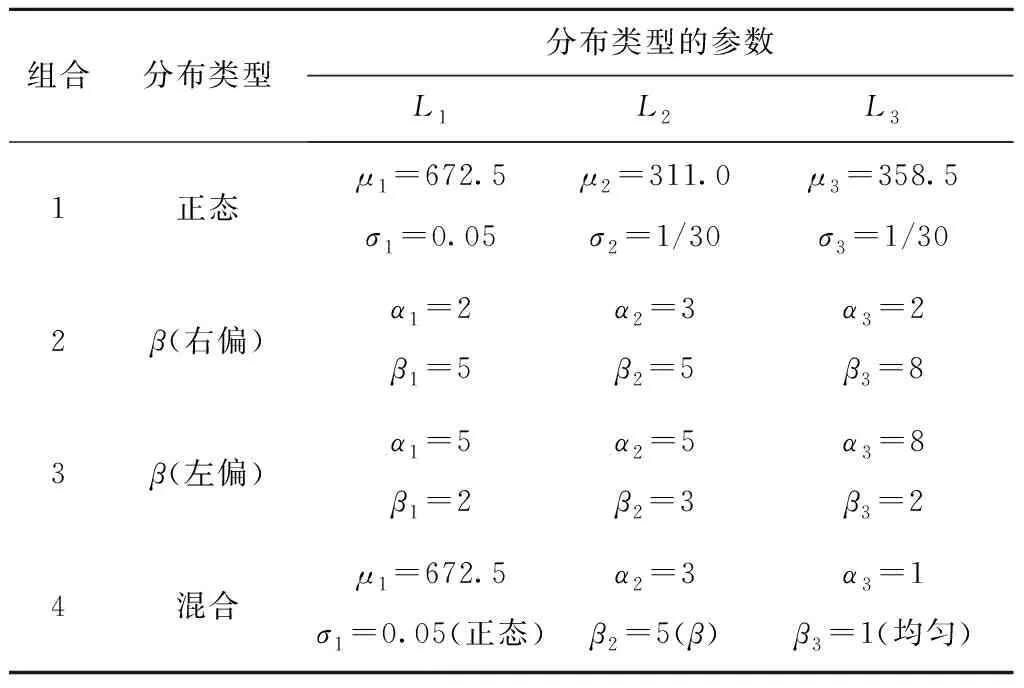
表3 各组成环的分布类型及参数

以组合2为例，当各组成环服从β分布(右偏)时，可计算得到各个组成环的均值、方差、偏度和峰度，如表4中第2～5行所示。根据式(29)～式(33)和式(24)，可得各组成环的水平值lij(i=1,2,3为因素，j=1,2,3为水平)和相应的权重因子ωij，如表4中第6～7行所示。

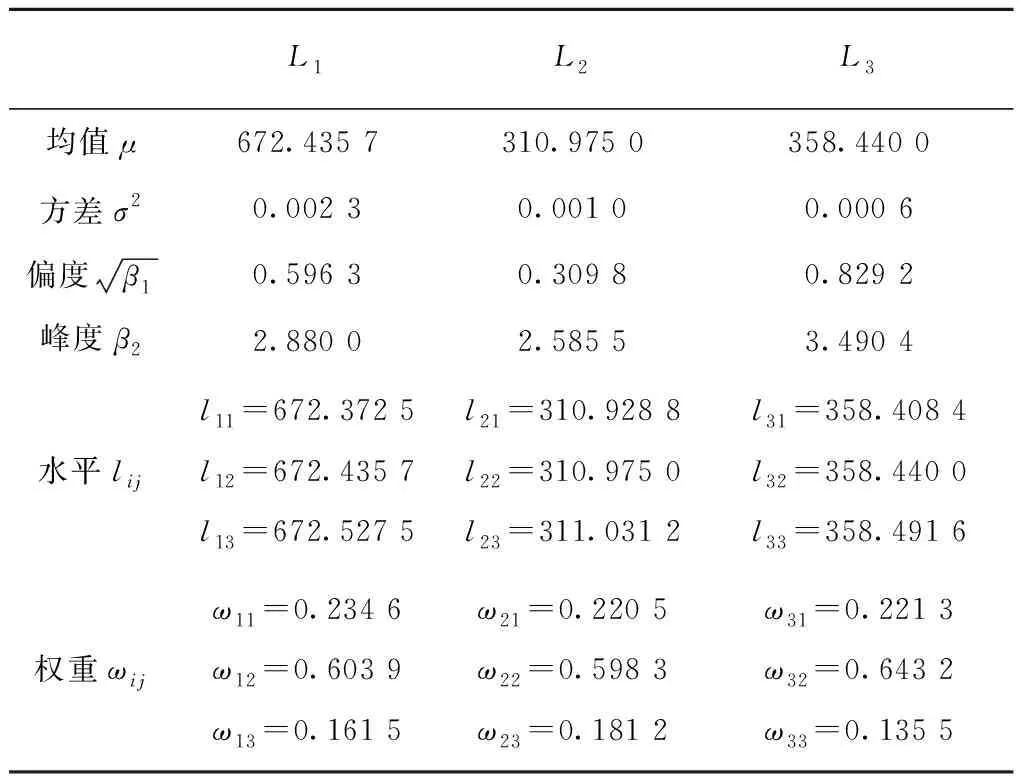
表4 组合2中各组成环的统计参数及水平、权重值

试验设计如表5所示，表中第4列为与组成环水平对应的权重因子的乘积，第5列为根据式(45)计算的间隙值。根据表5中的数据可以得到装配间隙δ的27个样本值。

根据式(38)～式(41)得到的装配间隙的均值、方差、偏度和峰度如表6中第5列所示，表6同时给出了其余组合的计算结果。用蒙特卡洛方法模拟1×106次的仿真结果也列于表6中。

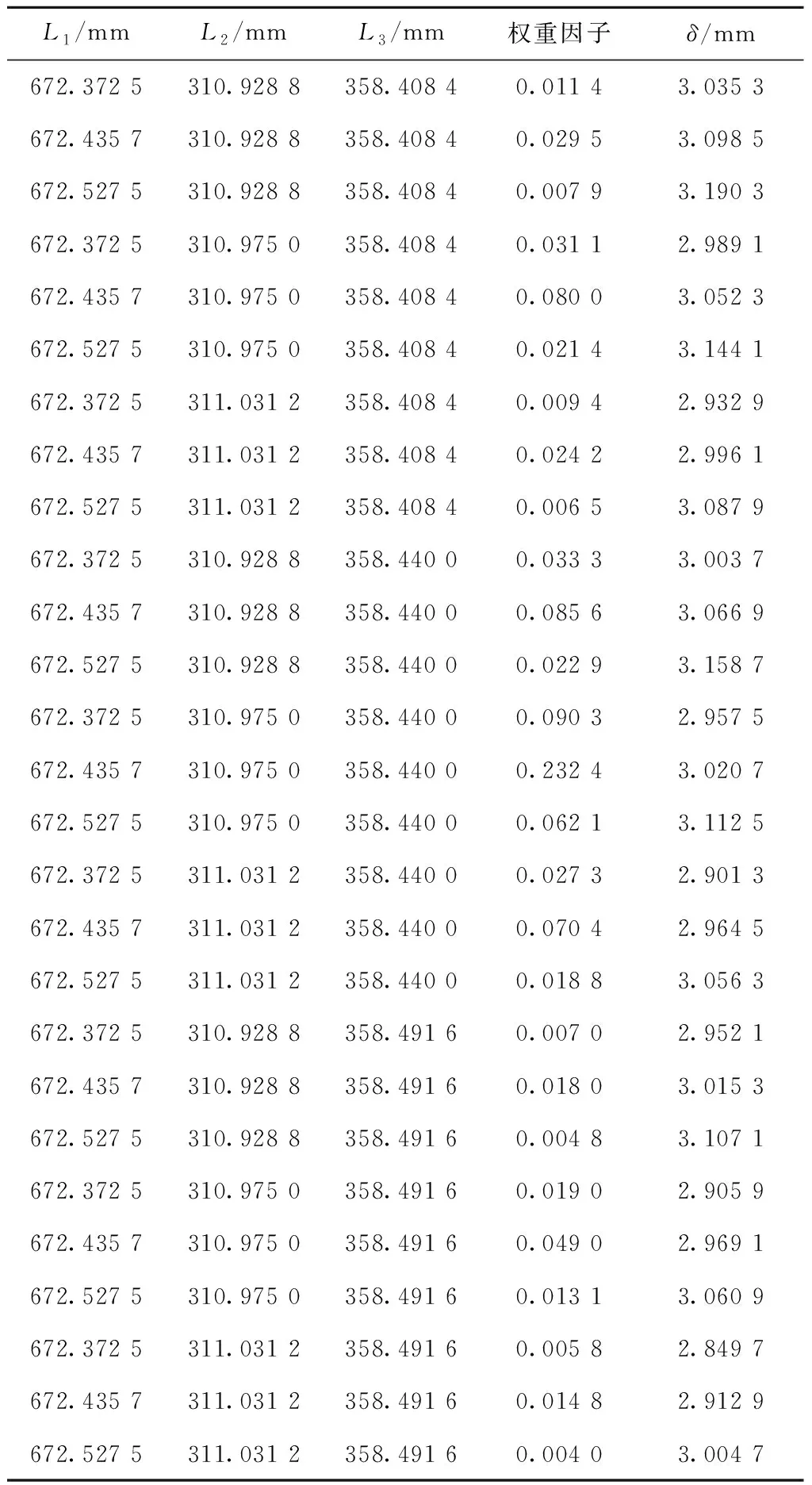
表5 正交试验表

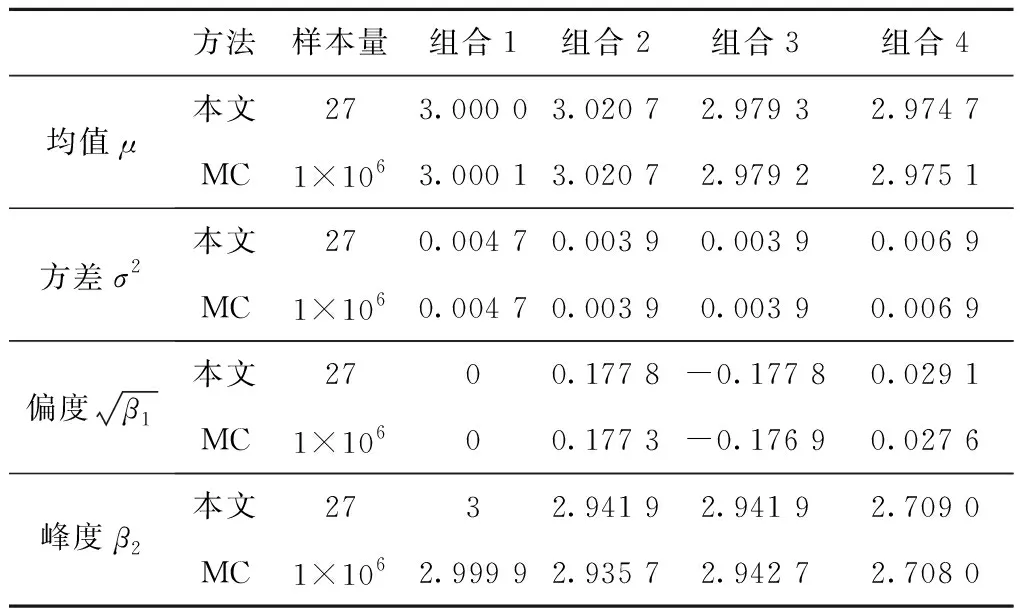
表6 封闭环偏差分布参数

注：表中MC表示蒙特卡洛方法。

由表6可知，在4种组合中，本文方法用27个样本量计算出的封闭环尺寸变量的均值、方差、偏度和峰度，与蒙特卡洛方法1×106个样本量得出的结果非常接近，最大相对误差出现在组合4中对偏度的估计，为5.43%。结果表明，本文方法不仅适用于组成环尺寸变量分布为正态的情况，还适用于非正态分布的情况同样适用；并且本文方法的计算样本量为27,这与蒙特卡洛方法动辄十万、百万的样本量需求相比，本文方法在计算次数和效率上具有明显优势，在保证计算精度的前提下弥补了蒙特卡洛法在计算效率上的不足。

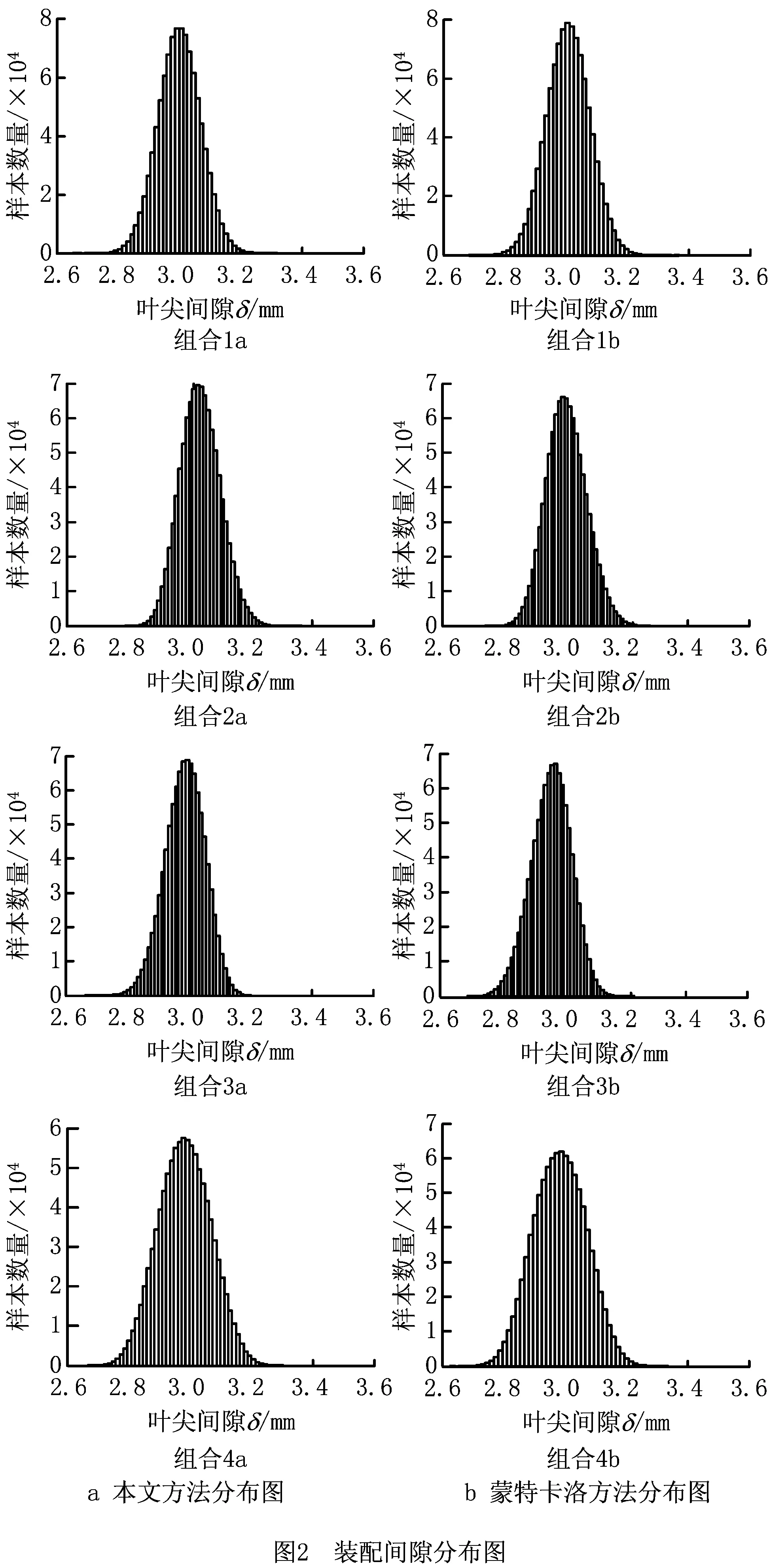
在计算得到装配响应的均值、方差、偏度和峰度后，根据Pearson分布理论，应用MATLAB中的Pearsrnd函数进行1×106的模拟，得到装配间隙的分布如图2所示，其中a为本文方法得到的分布图，b为蒙特卡洛方法得到的分布图。通过对比发现，用本文方法得出的分布图和用蒙特卡洛方法得出的分布图的吻合度很高。

3.2 装配成功率计算

根据Pearson统一模型和表6中的数据，用本文改进的田口试验法得到的各个组合下装配间隙δ的分布类型如表7中第2行所示，并且各个组合下分布的统计系数已知，由此计算的装配成功率如表7第3行所示。表7同时给出了进行1×106次蒙特卡洛模拟得出的装配成功率。

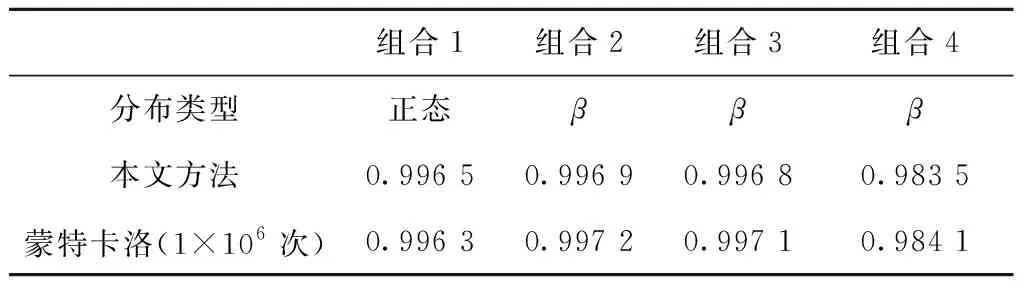
表7 装配成功率计算结果

通过对比可见，装配成功率为P=Pr(2.8 mm≤δ≤3.2 mm)时，用本文改进的田口试验法计算得出的装配成功率与经过1×106次蒙特卡洛模拟得出的结果非常接近，4种组合中的最大相对误差仅为0.06%，证明在对装配成功率进行估算时，本文改进的田口试验法在计算精度上与蒙特卡洛方法相当。

4 结束语

本文针对传统的田口试验方法在公差分析中缺乏理论证明、只对尺寸分布为正态分布的情况有效、无法准确估计统计量的高阶矩等缺点，提出改进的田口试验方法。在理论推导证明的基础上，结合Pearson分布理论，建立了装配公差分析模型，形成了基于改进田口试验法的装配公差分析方法。将该方法应用于某型航空发动机涡轮转子的径向装配公差分析，通过与蒙特卡洛仿真结果对比，证明了本文方法的有效性和实用性。

本文用到了三水平全因子试验设计，所需的试验次数为27次，当组成环数量较多时(N≥10)，所需的试验次数将会呈指数增长，使计算效率大大降低。针对该问题，可通过采用两水平部分因子试验设计代替三水平全因子试验设计，来减少试验次数和计算量，未来还可以考虑实现该方法的软件功能模块应用。

参考文献:

[1] ZHANG Yan, MO Rong. Assembly tolerance analysis method based on low discrepancy sequences sample[J]. Computer Integrated Manufacturing Systems,2014,20(3):579-585(in Chinese).[张 岩,莫 蓉.基于低偏差序列样本的装配公差分析方法[J].计算机集成制造系统,2014,20(3):579-585.]

[2] SINGH P K, JAIN P K, JAIN S C. Important issues in tolerance design of mechanical assemblies. Part 1:tolerance analysis[J]. Proceedings of the Institution of Mechanical Engineers Part B Journal of Engineering Manufacture,2009,223(10):1225-1247.

[3] ZHU Bin, YU Naijiang, MENG Xianghai, et al. Study on the tolerance analysis of aircraft engine assembly dimension chain[J]. Journal of Test and Measurement Technology,2015,29(2):177-184(in Chinese).[朱 彬,于乃江,孟祥海,等.航空发动机装配尺寸链公差设计方法研究[J].测试技术学报,2015,29(2):177-184.]

[4] MANSUY M, GIORDANO M, HERNANDEZ P. A new calculation method for the worst case tolerance analysis and synthesis in stack-type assemblies[J]. Computer-Aided Design,2011,43(9):1118-1125.

[5] SEO H S, KWAK B M. Efficient statistical tolerance analysis for general distributions using three-point information[J]. International Journal of Production Research,2002,40(4):931-944.

[6] WANG Jing, SHI Hong, HUANG Xiaofei, et al. Assembly tolerance analysis for aeroengine based on Monte Carlo simulation[J]. Journal of Shenyang Institute of Aeronautical Engineering,2010,27(4):8-11(in Chinese).[王 晶,石 宏,黄笑飞,等.基于蒙特卡罗模拟法的航空发动机装配公差分析[J].沈阳航空航天大学学报,2010,27(4):8-11.]

[7] FONSECA J R, FRISWELL M I, LEES A W. Efficient robust design via Monte Carlo sample reweighting[J]. International Journal for Numerical Methods in Engineering,2007,69(11):2279-2301.

[8] CAO Yanlong, YAN Huiwen, LIU Ting, et al. Application of Quasi-Monte Carlo method based on good point set in tolerance analysis[J]. Journal of Computing & Information Science in Engineering,2016,16(2):021008.

[9] XIAO Renbin, ZOU Hongfu, TAO Zhenwu. Multi-bojective model of tolerance design and its solution with particle swarm optimization algorithm[J]. Computer Integrated Manufacturing Systems,2006,12(7):976-980(in Chinese).[肖人彬,邹洪富,陶振武.公差设计多目标模型及其粒子群优化算法研究[J].计算机集成制造系统,2006,12(7):976-980.]

[10] LIU S G, WANG P, LI Z G. Non-normal statistical tolerance analysis using analytical convolution method[J]. Journal of Advanced Manufacturing Systems,2008,7(1):127-130.

[11] LI Zhengang, LIU Shaogang, ZHANG Dake, et al. Application of hybrid convolution in statistical tolerance analysis[J]. Computer Integrated Manufacturing Systems,2008,14(3):462-465(in Chinese).[李振刚,刘少岗,张大克,等.混合卷积在统计公差分析中的应用[J].计算机集成制造系统,2008,14(3):462-465.]

[12] GHANI J A, CHOUDHURY I A, HASSAN H H. Application of Taguchi method in the optimization of end milling parameters[J]. Journal of Materials Processing Technology,2004,145(1):84-92.

[13] QIAN Zepeng, YU Tao, LIU Ruihong, et al. Optimum design of tolerance dimension chain based on Taguchi[J]. Coal Mine Machinery,2011,32(1):122-124(in Chinese).[钱泽鹏,于 涛,刘瑞红,等.基于Taguchi的公差尺寸链的优化设计[J].煤矿机械,2011,32(1):122-124.]

[14] FENG Changxue, KUSIAK A. Robust tolerance synthesis with the design of experiments approach[J]. Journal of Manufacturing Science & Engineering,2000,122(3):520-528.

[15] MUTHU P, DHANALAKSHMI V, SANKARANARAYANASAMY K. Optimal tolerance design of assembly for minimum quality loss and manufacturing cost using metaheuristic algorithms[J]. International Journal of Advanced Manufacturing Technology,2009,44(11/12):1154-1164.

[16] TAGUCHI G. Performance analysis design[J]. International Journal of Production Research,1978,16(6):521-530.

[17] TAGUCHI G, CHOWDHURY S, WU Y. Taguchi’s quality engineering handbook[M]. New York,N.Y.USA:Wiley,2005.

[18] WEN Zejun, ZHU Zhengqiang, ZHOU Zhijin, et al. One-dimensional assembly success rate calculation method based on Taguchi orthogonal test and its application[J]. Journal of Hunan University of Science & Technology:Natural Science Edition,2011,26(3):26-30(in Chinese).[文泽军,朱正强,周知进,等.基于Taguchi正交试验的一维装配成功率计算方法及其应用[J].湖南科技大学学报：自然科学版,2011,26(3):26-30.]

[19] D’ERRICO J R, ZAINO N A. Statistical tolerancing using a modification of Taguchi’s method[J]. Technometrics,1988,30(4):397-405.

[20] ZHANG Qingli, WANG Xiaomei, YIN Shaotang, et al. High accuracy calculation of high order Gaussian integral nodes[J]. Engineering Sciences, 2008, 10(2):35-40(in Chinese). [张庆礼, 王晓梅, 殷绍唐,等. 高阶高斯积分节点的高精度数值计算[J]. 中国工程科学, 2008, 10(2):35-40.]

[21] ENGEL H. Numerical quadrature and cubature[M]. London,UK:Academic Press,1980.

[22] BIAN Haihong, ZHENG Weigao, LIN Zhangsui, et al. Modeling and application of output statistics of cluster wind farm[J]. Electric Power Automation Equipment,2015,35(12):21-27(in Chinese).[卞海红,郑维高,林章岁,等.集群风电场出力统计指标建模与应用[J].电力自动化设备,2015,35(12):21-27.