新订单与时间窗口混合驱动的继承性虚拟单元重构

韩文民，余 义，高龙龙，方锦烽，李正义

(江苏科技大学 经济管理学院，江苏 镇江 212003)

0 引言

随着市场竞争的加剧，制造企业面临着日益频繁且难以预测的市场变化，为保持竞争力，企业不仅需要高效地生产高质量产品，还要能够及时响应快速变化的市场和消费者需求，因此多品种、小批量的订单式生产(Make-To-Order manufacturing, MTO)成为制造业发展的主流。为有效应对这一发展趋势，突破设备物理位置不能或难以改变的障碍，具有提高生产制造柔性及敏捷性优势的虚拟单元生产模式应运而生[1]。虚拟单元生产系统(简称虚拟单元)主要根据工件工艺相似性将工件聚类为工件族，并将生产资源在逻辑上分配给相应的工件族进行调度生产，加工任务结束后虚拟单元中的设备会自动释放，以供其他虚拟单元使用。在虚拟单元生产过程中，随着新订单的陆续随机到达，原有的虚拟单元结构可能不适应后期的加工需求，因此虚拟单元重构频繁发生。

目前，有关驱动单元重构或重调度方式的研究得到了国内外学者的广泛关注。Gürel等[2]研究了设备故障等事件驱动下的重调度问题，构建了考虑压缩工件加工时间带来的额外成本，以及干扰造成的未按时完工的工件数最小化双目标模型；Shen等[3]考虑常规订单、急件订单等事件驱动下的重调度问题，提出求解该问题的多目标演化算法；Zhang等[4]研究了急件、任务取消等事件驱动下的重调度问题，提出多代理和蚁群算法混合的处理方法；Rezazadeh等[5]研究了考虑周期的虚拟单元构建问题，提出解决该问题的粒子群和模拟退火混合算法；Mahdavi等[6]研究了时间周期驱动的多目标虚拟单元构建问题，并利用模糊目标规划进行求解；Paydar等[7]讨论了带模糊参数的、时间周期驱动的多目标虚拟单元构建问题，并使用修订多重选择目标规划方法求解问题；Moradgholi等[8]研究了在时间周期驱动下的双目标模糊规划模型，并使用遗传算法进行求解。应该看到，单纯事件驱动可能因频繁变动导致生产计划的“神经质现象”，单纯周期驱动则容易导致生产系统不能及时响应生产系统内外条件的动态变化，虽然有些文献考虑了事件—周期的混合驱动，但大多为单一驱动方式的简单叠加，导致单元重构及调度更加频繁[9-10]。

继承性虚拟单元重构指在单元重构时，不仅要使重构单元的生产高效运行，还要考虑稳定性的重要指标，即尽可能地继承原有虚拟单元的配置形式，减少频繁调整对生产系统带来的冲击。目前，在虚拟单元重构文献中，大多以时间(最长完工时间、平均延误时间、平均流程时间等)或成本作为重构评价标准[6-7,11-13]，没有考虑重构的继承性指标，而将单元结构进行全局调整。频繁大规模变动的重构会使生产调度更为复杂，从而造成物流紊乱，进而带来更多的重置成本和物料搬运成本，增加工人的生产压力，同时还会给生产的过程控制和质量控制带来很多隐患[14-15]。因此，如何兼顾重构后单元生产的高效性与稳定性，即继承性的单元重构，具有重要的意义。Wu等[16]研究了机器故障下的重构问题，其所考虑的继承性指标为工序开始时间及工序顺序的变化，Vieira等[17]提出制造系统的重构框架模型，明确了稳定性是系统重构的重要评价标准；Li等[18]研究了新订单到达后的虚拟单元重调度问题，以重构前后单元内设备数量的改变作为继承性指标。

在企业实际生产过程中，需要根据未来多个计划期的市场需求构建多期虚拟单元方案。然而，在实施虚拟单元生产过程中，新订单会随机到达生产车间[10]。针对这种扰动，为保证生产过程组织的稳定性，本文在新订单与时间窗口相结合的混合驱动方式下，对虚拟单元进行重构。若单元的剩余加工能力能够满足新订单的生产需求，则采用订单驱动的重构方式，在当期利用剩余设备能力仅按照高效性指标进行虚拟单元构建；若单元内剩余设备加工能力不能满足新订单的生产需求，则在当期利用剩余设备能力将可以完成的任务仅按高效性指标进行虚拟单元构建，不能完成部分当期采用时间窗口冻结技术将新订单未完成部分进行冻结，到本期生产结束后，再将新订单加入后期虚拟单元进行生产。后期的虚拟单元重构不仅要使后续虚拟单元生产高效运行，还应最大程度地继承原有虚拟单元的配置形式，减少单元频繁重构对生产的冲击。为此，本文在现有研究基础上，提出继承性的虚拟单虚拟单元重构方案。该重构方法综合考虑了虚拟单元重构的高效性与稳定性特征(高效性包括产品工艺相似性、跨单元次数、设备利用率、物流成本因素，稳定性包括单元内设备数量及类型的变动因素)，构建了非线性多目标整数规划模型，为了有效地求解模型，在相关算法研究基础上[5,6,19,20]设计了基于动态层次分析的多目标遗传优化算法，该算法通过随机搜索Pareto优化解集实现了对模型的有效求解。

1 新订单下的继承性虚拟单元重构

1.1 新订单下的继承性虚拟单元重构问题及假设

新订单到达时的虚拟单元重构问题可描述为：车间内的原有虚拟单元数为c(c=1,2,…,C)个，可供加工的设备数为m(m=1,2,…,M)台，原加工工件数为i(i=1,2,…,I)件，这里各工件包括j(j=1,2,…,Ji)道工序。在t时刻，新订单i′(i′=1,2,…,I′，I′表示到达新工件的总数)到达车间，则车间工件数量为I+1,I+2,…,I+I′。

为更好地构建模型，现对虚拟单元制造系统作如下假设：①各工件的各期需求量已知；②各工件需要不同类型的机床对其进行多道工序加工，且工艺顺序与加工时间已知；③每台机床在同一时间内只能加工一道工序；④同一工件的同一工序只能在一台机床上加工完成；⑤新订单到达时，若现有设备的剩余加工能力不能满足其生产需求，则只对尚未加工工件的工序进行虚拟单元重构，即在某机床上正在加工的工件工序也不受影响，直至加工完成，已加工完成的工件工序也不受影响，重构时不予考虑；⑥不考虑机床故障。

1.2 新订单下的继承性虚拟单元重构模型

1.2.1 参数定义

c为第c个虚拟单元，c=1,2,…,C；

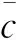
t为第t个虚拟单元生产计划期，t=1,2,…,T；

i为第i个加工工件，i=1,2,…,I；

j为加工工件的第j道工序，j=1,2,…,Ji；

m,k为第m或k台设备，m,k∈1,2,…,M，m≠k；

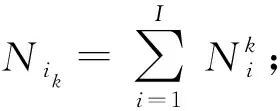
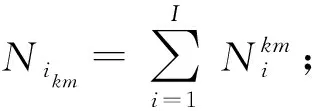
βij为工件i的工序j的单位移动成本；

d(mi,j→mi,j+1)为加工工件i的工序j和工序j+1的设备之间的距离；

Dit为工件i在计划期t的需求量；

Bi为工件i的生产批量；

Oik为单位生产批量工件i在设备k上的加工时间；

Ack为重构前设备所属的虚拟单元状态，Ack=1表示设备k属于单元c，Ack=0表示设备k不属于单元c；

Ztcij为重构前工件i中工序j所属的单元状态，Ztcij=1表示计划期t内工件i的第个j工序在虚拟单元c中加工，否则Ztcij=0；

DLi为工件i的交货期；

Stemin为所有重构方案中的最少跨单元次数；

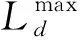
Fi为工件i所需的加工流程时间；

Ej为工序j的完成时间；

Sj为工序j的开工时间；

Ocm为设备m在虚拟单元c中某时刻加工的工序数；

Nim为工件i在设备m上加工的工序数。

1.2.2 决策变量

为虚拟单元方案调整前与调整后包含虚拟单元总数的较小值，此处单元调整后虚拟单元数量的增加或减少不算对原虚拟单元结构的调整。

1.2.3 模型构建

(1)工艺相似性指标 工艺相似性是虚拟单元构建的基础，且将相似产品聚类为待加工工件族进行连续生产后可减少生产准备时间，增加工人熟练程度，从而提高效率，保障产品质量，因此该指标是实现虚拟单元生产高效性的重要基础之一。工艺相似性指标

(1)

(2)物流成本指标 考虑虚拟单元具有不改变设备的物理布局而形成逻辑上相互关联的虚拟动态实体进行工件加工的特性，生产计划的变更可能导致待加工工件在制造设备间流转频繁，进而造成物流紊乱和物流成本增加。因此，在高效性指标方面要充分考虑物流成本指标f2，

(2)

式(2)表示各计划期中所有待加工工件按加工工序顺序选中的设备距离与该工序单位移动成本之积。

(3)跨单元次数指标 实际生产过程中，工件跨单元加工会影响生产的连续性，增加设备与工装的调整时间和费用以及管理工作量，从而降低了虚拟单元生产效能。因此，高效性指标中要考虑工件跨单元移动次数指标f3，

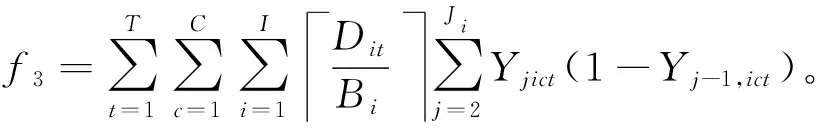
f3=∑Tt=1∑Cc=1∑Ii=1DitBi∑Jij=2Yjict(1-Yj-1,ict)。

(3)

式(3)表示各计划期内构建的虚拟单元中各加工工件的所有加工工序是否都在该单元内部完成。式中·表示取小于内部值的最大整数。

(4)设备利用率指标 研究表明，较低的设备利用率将导致设备投资费用增加、人员费用增加、资产回报率低。用最小化设备负载与最大设备能力间的比值表述设备利用率：

(4)

因此，在新订单到达情况下的生产高效性指标表述为

f={f1,f2,f3,f4}。

(5)

式中：工艺相似性指标f1取最大值,以使相似工件尽可能在同一单元内完成加工，从而减少调整时间；f2取最小值,以降低工件加工过程中的物流成本；f3取最小值,以减少调度的复杂性；f4取最大值,以提升设备利用率，降低加工成本。

在新订单到达的情况下，生产高效性指标越高，表示单元的生产效率越高，其表达式为

F1=maxf。

(6)

式中虽然各目标选取的极值不同，但是应保持整体最大，以保证系统整体最优。

稳定性指标是继承性虚拟单元重构与非继承性虚拟单元重构的主要区别。优化调整后的虚拟单元与原有虚拟单元间的差别，即单元内部设备变动越小，该方案的稳定性越高。其表达式为

(7)

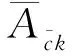
因此，针对新订单到达的虚拟单元重构的多目标规划模型如下：

目标函数为

F={F1,F2}。

(8)

s.t.

j=1,2,…,Ji,i=1,2,…,I,c=1,2,…,C,

m∈1,2,…,M;

(9)

Mcm={0，1}，

c=1,2,…,C,m∈1,2,…,M;

(10)

Ej≤Sj+1，j=1,2,…,Ji;

(11)

(12)

Xkc≤Nkc，c=1,2,…,C,k∈1,2,…,M;

(13)

(14)

(15)

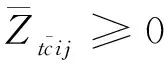
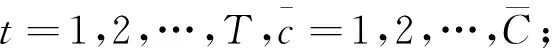
i=1,2,…,I,j=1,2,…,Ji;

(16)

Xjim，Xjicm，Yjict为0-1变量。

(17)

其中：式(9)表示所有工件的一道加工工序只能被分配到一个虚拟单元内的一台设备上加工；式(10)表示每台设备在某时刻只能属于一个虚拟单元,且每次最多只能分配到一道工序；式(11)表示只有上道工序完工,下道工序才能开始；式(12)限制了所构建虚拟单元总数不超过规定的上限；式(13)限制了虚拟单元内加工设备数量不超过规定的上限；式(14)～式(16)表示决策变量的非负整数约束；(17)表示0-1变量约束。

该模型属于非线性多目标整数规划模型，因为模型为多目标且物流成本指标、跨单元次数指标具有非线性的特征，数学规划算法难以有效求解模型，所以本文设计智能算法求解模型。

2 算法设计

本文构建的模型为非线性多目标整数规划模型，随着订单数、设备、虚拟单元个数、计划期数的增加，模型的求解将变得非常复杂困难。因此，设计基于遗传算法的多目标优化算法来求解模型。

2.1 编码与解码

染色体的编码是实现多目标遗传算法的基础，根据模型约束条件(每个工件的工序加工顺序确定等)和决策变量要求，文中采用分段编码的方法进行编码，染色体由单元分配(设备)、单元分配(工件)、工序机器选择和工件排序4部分组成。考虑以工件数I、每个工件加工工序J、设备类型M、单元数C等参数进行编码，图1所示为总工件数I=3，每个工件加工工序J=3，设备类型M=5，单元数C=3的编码过程。

图1中，单元分配部分的数字为机器(工件)所属的单元号，例如机器M1的单元分配号为3，表示将它分配到单元3中；工序机器选择部分的数字为该工序可选机器集中对应的机器编号，例如工件1工序1的机器选择数字为3,则该工序在可选机器集中选择对应的机器M4进行加工；工件排序部分的数字为工件的编号，例如第1个“1”表示工件1的工序1第1个开始加工，第2个“1”表示工件1的工序2排在第3个加工。

2.2 选择操作

选择操作是为了保证解的质量而进行优胜劣汰，使优秀且拥挤密度比较小的个体参与下一代进化。为了避免算法在目标空间一个固定点的区域采样，本文算法采用随机权重在整个Pareto前沿面均匀采样。同时，为有效引导选择出满意的优良基因，采用一致矩阵法对各目标函数进行罚函数处理，从而为不同个体赋予不同的选择概率，以保证每次迭代所选择的解的优越性，从而加快收敛速度[21]。多目标模型的随机权重和目标可表示为：

(18)

(19)

(20)

式中α表示敏感因子，根据实际情况取值为0，1，2，3。

最后，通过式(21)对第i个待评价方案进行综合评价，并得到惩罚系数θi。

(21)

2.3 交叉与变异操作

为使更新的种群在满足模型约束的基础上具有更好的遗传父代有利基因的能力，采用基于工序编码的优先交叉操作(Precedence Operation Crossover，POX)。首先，选定需要交叉的两条染色体，并随机选中一个工件的编号;然后，将第2条染色体中该编号的基因位置记录下来插入第1条染色体的对应位置;最后，将第1条染色体中的剩余基因依次放入剩下的基因位置。由此，便实现了交叉操作,具体的交叉过程如图2所示。

为保持群体的多样性，采用插入变异的方式，即随机选取某一基因或基因片段，插入另一个不同的随机位置。

3 实例分析

以某船厂机加工车间的实际生产订单为例进行实例分析。新订单出现后，首先需要对现有剩余设备的加工能力进行衡量，当剩余设备加工能力满足新订单生产时，虚拟单元的构建过程较为简单，实例分析不展开讨论。本实例主要在剩余设备不足以满足新订单生产的情况下，对原虚拟单元进行继承性重构分析。可供加工的设备信息、生产车间所需加工工件的工序信息及设备之间的物流距离信息分别如表1～表3所示。

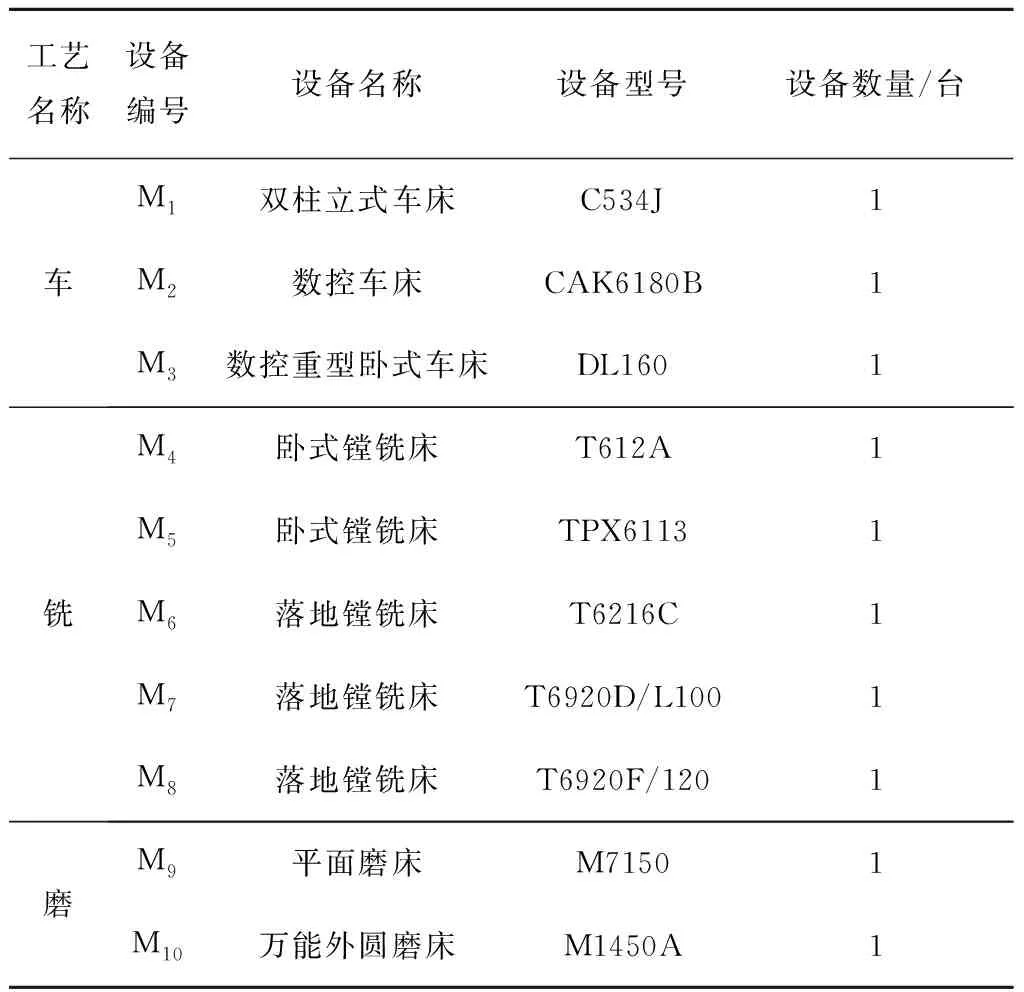
表1 设备的相关信息

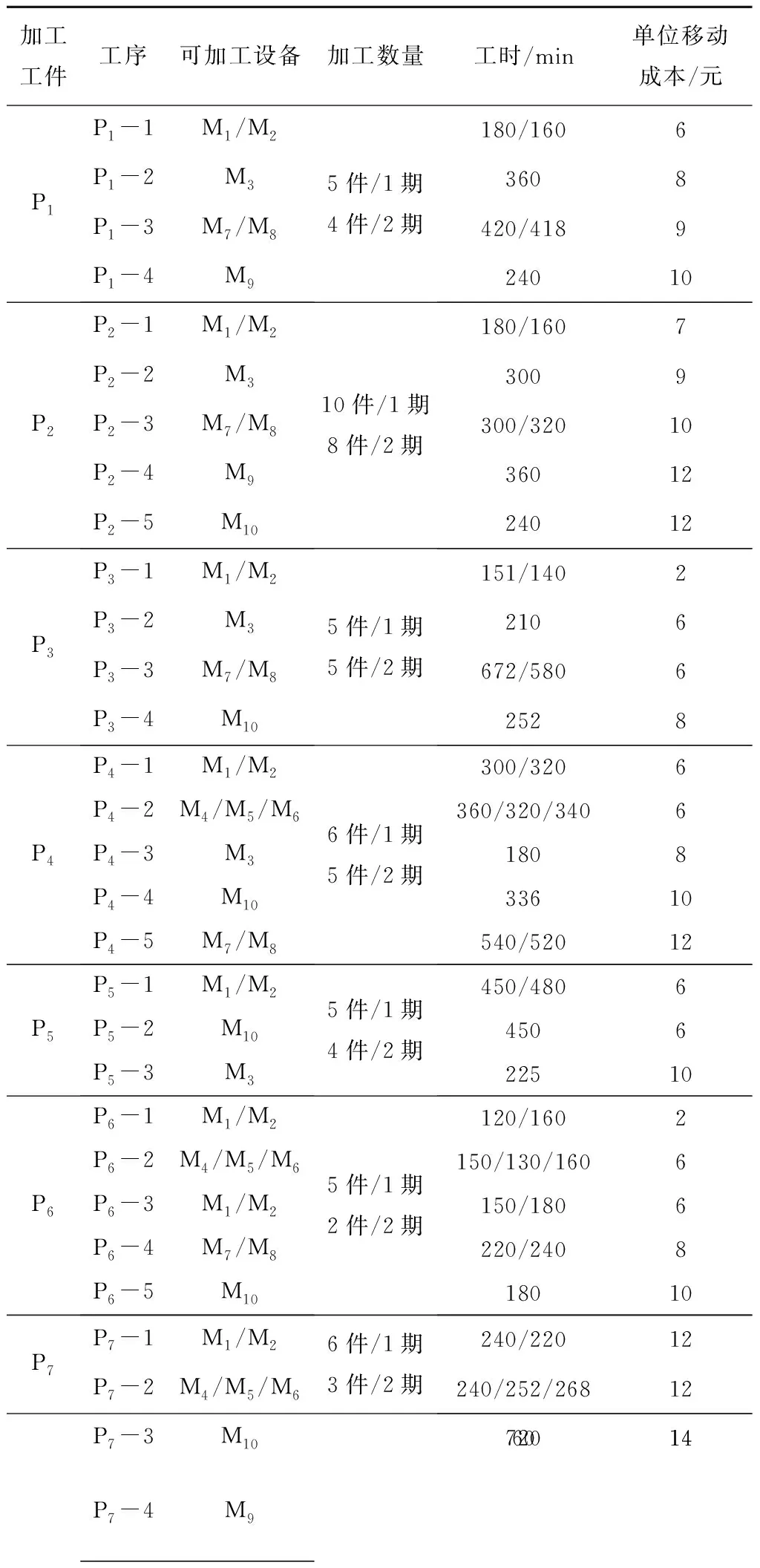
表2 加工工件的工序信息

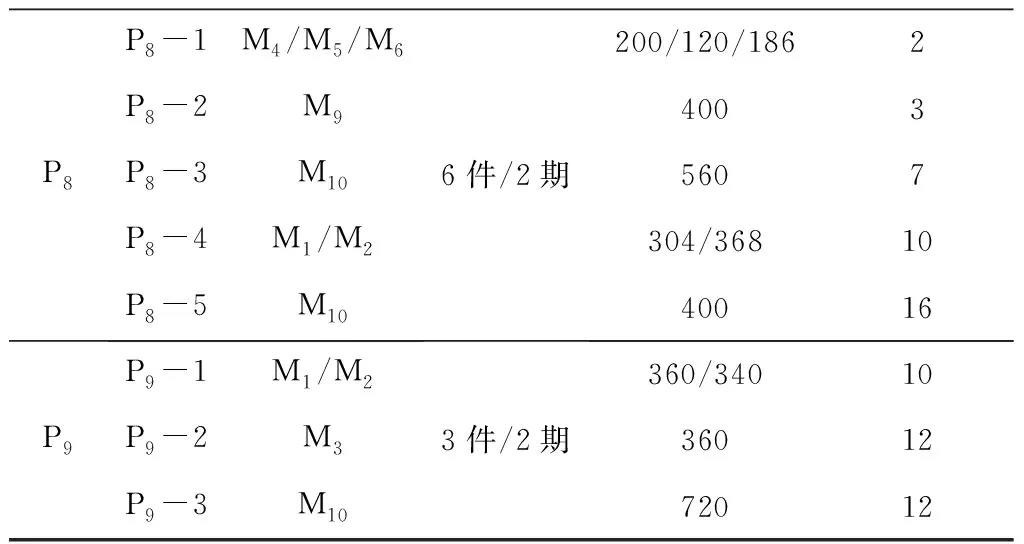
续表2

注：“可加工设备”列表明了能加工对应工序的所有设备，工件工序在相应设备上的加工时间为工件加工数量与对应工序单个工件在设备上的加工时间的乘积。

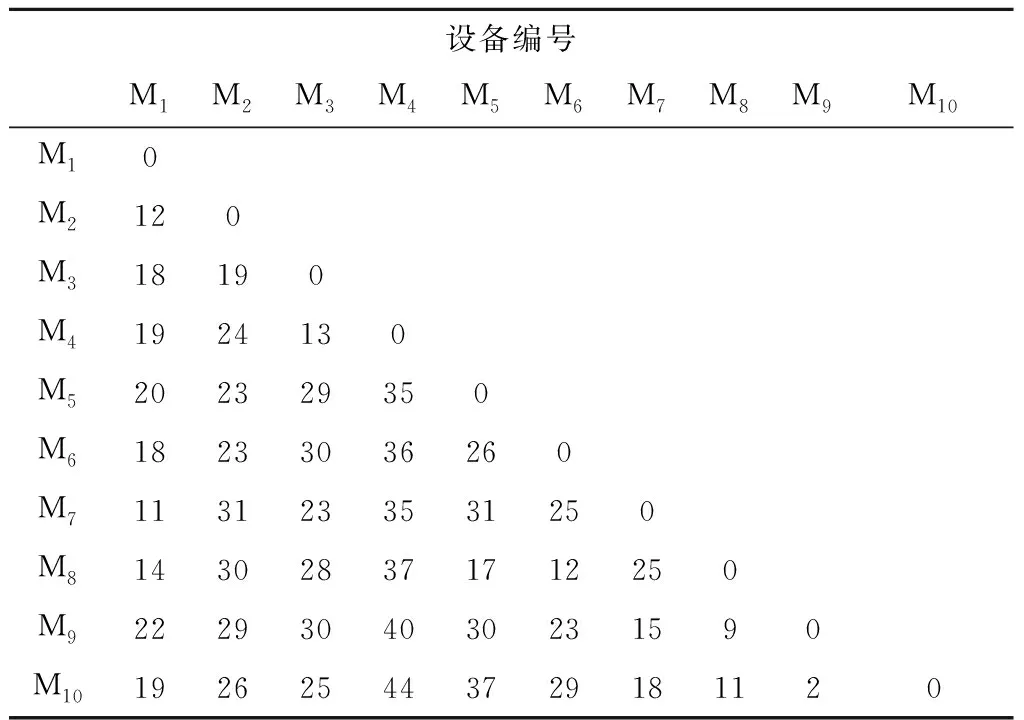
表3 各设备之间的物流距离信息 m

注：表中距离为曼哈顿距离。

本文采用MATLAB 2017a实现了虚拟单元继承性重构的算法求解。首先，在初始阶段根据待加工工件和工艺信息构建初始虚拟单元。本文多目标遗传算法的参数设置如下：种群数目为50，迭代次数为500，交叉概率为0.01，变异概率为0.8[22]。在构建初始虚拟单元时，考虑到各高效性指标中，跨单元次数和设备利用率在虚拟单元构建中均起辅助作用，因此给定各高效性指标权重分别为f1=0.4 ，f2=-0.3 ，f3=-0.15 ，f4=0.15。在计划期2中，采用继承性虚拟单元重构方案进行重构，得出的初始虚拟单元构建方案如表4所示，算法的收敛效果如图3和图4所示。

表4 初始虚拟单元构建方案

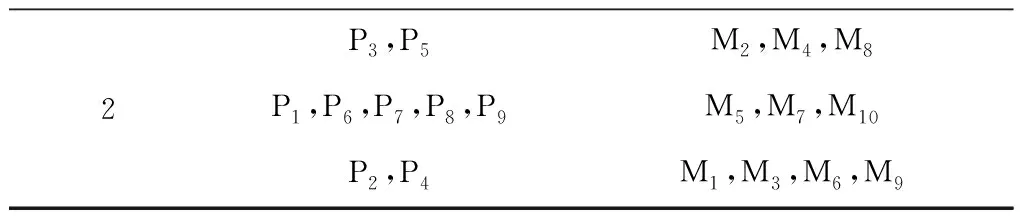
续表4

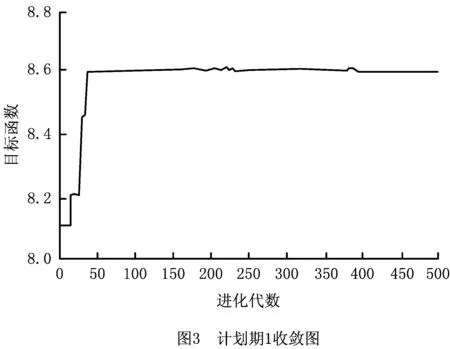
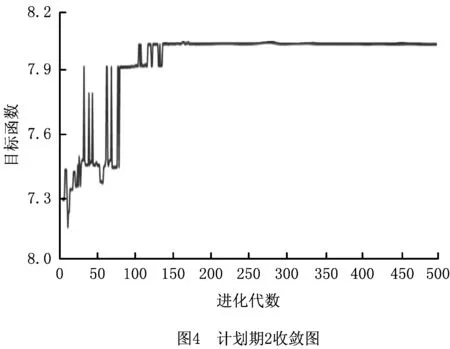
由表4可知，针对待加工工件和工艺信息计划期1与计划期2分别生成了3个虚拟单元，且3个虚拟单元均存在设备共享使用的情况，因此可以有效降低工件跨单元加工的次数，保证工件尽可能在相应的虚拟单元内完成生产。同时，因为在计划期2中采用继承性虚拟单元重构方案，所选方案基本保持计划期1中虚拟单元的配置形式，所以可以实现虚拟单元生产的持续性，避免重构幅度较大而导致的生产中断、准备成本过高、工人熟练度下降等问题。在计划期1的虚拟单元生产过程中出现新订单P10，P11插入的情况，此时应用计划期窗口冻结技术对计划期2中原有的虚拟单元进行快速继承性重构，以满足新订单加入下的生产需求。新订单P10，P11的工序信息如表5所示。

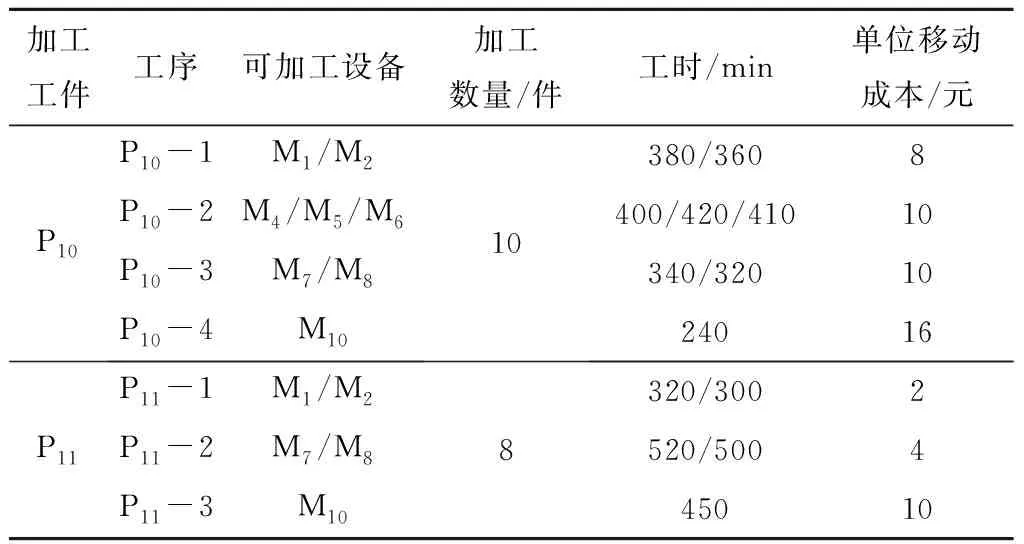
表5 新订单的工序信息

显然剩余生产设备不能够满足新订单的生产要求，因此在第1期加工任务完成后将新订单插入第2期，采用本文提出的包含生产高效性和生产稳定性的继承性虚拟单元重构方法进行虚拟单元重构，得到的虚拟单元构建方案如表6所示。

表6 虚拟单元继承性重构方案

根据重构后的虚拟单元可知，新订单P10，P11被共同分配至虚拟单元1对应的工件族，同时在虚拟单元1内增加了设备以同时满足原始订单和新订单的生产需求。将新订单采用文献[10]的方法进行重构，所得的方案及其对比如表7和表8所示，收敛图如图5和图6所示。

表7 虚拟单元模块化重构方案

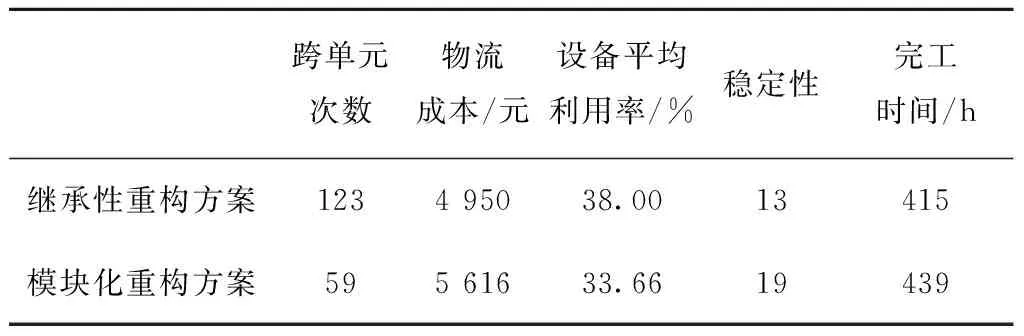
表8 虚拟单元重构方案对比

将继承性虚拟单元重构方案与模块化虚拟单元重构方案的结果，对比其跨单元次数、物流成本、设备利用率、稳定性指标和完工时间，对比结果如表8所示。其中，完工时间采用文献[23]的方法进行计算。

本文将所得结果与文献[24]所提方法的运算结果进行对比。由表8可见，文献[24]方法旨在有效减少跨单元物流次数，实现虚拟单元的敏捷性重构，与本文提出的继承性虚拟单元重构方案相比，其跨单元次数较少。但是，继承性虚拟单元重构方案减少了虚拟单元数、完工时间和物流成本，提高了设备利用率，更好地实现了设备共享。

同时与模块化虚拟单元重构方案相比，继承性的虚拟单元重构方案在稳定性指标方面有明显的优势，这将大大降低虚拟单元生产计划的变动幅度，减少单元内设备和任务的变动，避免因单元生产中物流紊乱、重置成本高昂，以及工人熟练度降低且产生消极情绪，而导致的生产效率降低等问题。另外，单元生产变动幅度小还有利于提高单元重构的速度和系统的敏捷性。

4 结束语

本文研究了新订单随机到达情况下，订单与时间窗口混合驱动的继承性虚拟单元重构。在虚拟单元重构中，采用了订单与时间窗口相结合的驱动方法，并考虑了虚拟单元重构的继承性指标，一方面提高了企业应对新订单随机到达所产生的扰动的响应能力，另一方面在维持虚拟单元高效生产的同时，保持了原有虚拟单元配置的稳定性。为此，本文构建了一个非线性多目标整数规划模型，并设计了基于动态层次分析的多目标遗传优化算法以求解模型，通过随机搜索Pareto优化解集，寻求继承性虚拟单元重构方案。实例分析表明，与非继承性虚拟单元重构相比，继承性虚拟单元重构在减少跨单元生产次数和完工时间、提高设备利用率及降低单元生产物流成本等方面具有明显优势。

为更好地反映生产实际情况，未来可研究新订单中带有紧急订单、出现设备故障，以及订单的加工时间和交货期不确定等情况下的继承性虚拟单元重构问题，同时在继承性虚拟单元重构中集成单元生产调度，进行虚拟单元重构与生产调度集成的全局优化决策。

参考文献:

[1] HAN Wenmin, GAO Longlong, WENG Hongbing, et al. Research on virtual cell scheduling of pipe processing in ship building based on theory of blocking flow[J].Shipbuilding of China,2016,57(3):164-175(in Chinese).[韩文民,高龙龙,翁红兵,等.基于阻塞流理论的船舶建造中管件加工虚拟单元调度问题研究[J].中国造船,2016,57(3):164-175.]

[2] GUREL S, CINCIOGLU D. Rescheduling with controllable processing times for number of disrupted jobs and manufacturing cost objectives[J]. International Journal of Production Research,2015,53(9):2751-2770.

[3] SHEN Xiaoning,YAO Xin. Mathematical modeling and multi-objective evolutionary algorithms applied to dynamic flexible job shop scheduling problems[J]. Information Sciences,2015,298:198-224.

[4] ZHANG Sicheng, WONG T N. Flexible job-shop scheduling/rescheduling in dynamic environment:a hybrid MAS/ACO approach[J]. International Journal of Production Research,2017,55(11):3173-3196.

[5] REZAZADEH H, MAHINI R, ZAREI M. Solving a dynamic virtual cell formation problem by linear programming embedded particle swarm optimization algorithm[J]. Applied Soft Computing,2011,11(3):3160-3169.

[6] MAHDAVI I, AALAEI A, PAYDAR M M, et al. Multi-objective cell formation and production planning in dynamic virtual cellular manufacturing systems[J]. International Journal of Production Research,2011,49(21):6517-6537.

[7] PAYDAR M M, SAIDI-MEHRABAD M. Revised multi-cho-

ice goal programming for integrated supply chain design and dynamic virtual cell formation with fuzzy parameters[J]. International Journal of Computer Integrated Manufacturing,2015,28(3):251-265.

[8] MORADGHOLI M, PAYDAR M M, MAHDAVI I, et al. A genetic algorithm for a bi-objective mathematical model for dynamic virtual cell formation problem[J]. Journal of Industrial Engineering International,2016,12(3):343-359.

[9] ADIBI M, ZANDIEH M, AMIRI M. Multi-objective scheduling of dynamic job shop using variable neighborhood search[J]. Expert Systems with Applications,2010,37(1):282-287.

[10] JIN Liangliang,ZHANG Chaoyong,SHAO Xinyu, et al. A study on the impact of periodic and event-driven rescheduling on a manufacturing system:an integrated process planning and scheduling case[J]. Proceedings of the Institution of Mechanical Engineers, Part B:Journal of Engineering Manufacture,2017,231(3):490-504.

[11] REZAZADEH H, GHAZANFARI M, SADJADI S J, et al. Linear programming embedded particle swarm optimization for solving an extended model of dynamic virtual cellular manufacturing systems[J]. Journal of Applied Research and Technology,2009,7(1):83-108.

[12] NIKOOFARID E, AALAEI A. Production planning and worker assignment in a dynamic virtual cellular manufacturing system[J]. International Journal of Management Science and Engineering Management,2012,7(2):89-95.

[13] AALAE A, DAVOUDPOUR H. Revised multi-choice goal programming for incorporated dynamic virtual cellular manufacturing into supply chain management:a case study[J]. Engineering Applications of Artificial Intelligence,2016,47:3-15.

[14] GIANGRECO A, PECCEI R. The nature and antecedents of middle manager resistance to change:evidence from an Italian context[J]. The international journal of human resource management,2005,16(10):1812-1829.

[15] LINES B C, SULLIVAN K T, SMITHWICK J B, et al. Overcoming resistance to change in engineering and construction:change management factors for owner organizations[J]. International Journal of Project Management,2015,33(5):1170-1179.

[16] WU S D, STORER R H, CHANG P C. One-machine rescheduling heuristics with efficiency and stability as criteria[J].Computers & Operations Research,1993,20(1):1-14.

[17] VIEIRA G E, HERRMANN J W, LIN E. Rescheduling manufacturing systems:a framework of strategies,policies, and methods[J].Journal of Scheduling,2003,6(1):39-62.

[18] LI Jingsheng,WANG Aimin,TANG Chengtong. Production planning in virtual cell of reconfiguration manufacturing system using genetic algorithm[J]. International Journal of Advanced Manufacturing Technology,2014,74(1/2/3/4):47-64.

[19] BAI Junjie, GONG Yiguang, WANG Ningsheng, et al. Methodology of virtual manufacturing cell formation in reconfigurable manufacturing system for make-to-order manufacturing[J]. Computer Integrated Manufacturing Systems,2009,15(2):313-320(in Chinese).[白俊杰,龚毅光,王宁生,等.面向订单制造的可重构制造系统中虚拟制造单元构建技术[J].计算机集成制造系统,2009,15(2):313-320.]

[20] LIAN Kunlei,ZHANG Chaoyong,GAO Liang, et al. Integrated process planning and scheduling using an imperialist competitive algorithm[J]. International Journal of Production Research,2012,50(15):4326-4343.

[21] WANG Xiaoqing, TANG Jiafu, GONG Jun, et al. Formation of multi-objective dynamic cells using random weight multi-objective genetic algorithm[J]. Chinese Journal of Management,2008,5(4):516-521(in Chinese).[王晓晴,唐加福,宫 俊,等.基于随机权重多目标遗传算法的多目标动态单元构建方法[J].管理学报,2008,5(4):516-521.]

[22] MOHAMMADI M, FORGHANI K. A hybrid method based on genetic algorithm and dynamic programming for solving a bi-objective cell formation problem considering alternative process routings and machine duplication[J].Applied Soft Computing,2017,53:97-110.

[23] GE Xianlong, WANG Xu, XING Lebin. Multi-vehicle scheduling problems and cloud GA based on the dynamic needs[J].Journal of System Engineering,2012,27(6):823-832(in Chinese).[葛显龙,王 旭,邢乐斌.动态需求的多车型车辆调度问题及云遗传算法[J].系统工程学报,2012,27(6):823-832.]

[24] JIA Guozhu, LUAN Shichao, CHEN Liang, et al. Cell formation problem for virtual cellar manufacturing based on the process modularization[J].Systems Engineering—Theory & Practice,2012,32(10):2111-2118(in Chinese).[贾国柱,栾世超,陈 亮,等.基于流程模块化的虚拟制造单元构建方法[J].系统工程理论与实践,2012,32(10):2111-2118.]