基于服务差异竞争的高铁快递纵向合作联盟
2018-06-30胡祥培
吕 璞,胡祥培
(1.大连理工大学 系统工程研究所,辽宁 大连 116024;2.大连交通大学 经济管理学院,辽宁 大连 116028)
0 引言
中国是目前全世界高铁运营里程最长的国家,截止2015年底,中国高速铁路运营线路总里程已达1.9万公里。同时,中国又是一个电子商务大国,电子商务的繁荣带来了巨大的快递业务量,2015年我国快递业务量突破200亿,成为当之无愧的世界第一。充沛的高铁运能和巨大的快递运输需求,催生了高铁快递这种新型的快递运输服务模式。由高铁承担干线运输,快递公司承担门到门揽、派件,双方形成快递运输服务供应链,这就是高铁快递的服务模式。与普通货运不同,快递运输不但要求将货物快速、准确地运达收货人,而且快递货物通常价值较高,要求货损率很低,还需要对货物进行全程信息跟踪。因此,高铁快递必须做到不同运输环节紧密衔接、协调一致和信息共享,从而要求高铁企业与快递公司在快递运输服务供应链上形成紧密的纵向合作联盟。在我国,铁路运输在一条线路上通常只有一家公司运营,而快递却有多家公司相互竞争,而且不同的快递公司在服务水平上也存在较大差异(如顺丰、EMS与一些小公司之间的服务水平差异),这种差异一方面反映了公司实力上的差距,另一方面也决定了快递公司在终端消费市场上的竞争力。因此,当一家高铁企业面对几家竞争性快递公司时,研究各方之间形成的竞争合作所达到的均衡,以及快递之间服务水平的差异带来的影响等,对促进高铁快递这一新兴快递模式的发展具有十分重要的意义。
在交通运输领域,企业间的合作运输联盟比较普遍,如星空联盟等。Da等[1-2]分别研究了零担运输承运人通过拍卖机制进行合作,以及零担运输承运人的合作优化问题和费用分配问题;Liu等[3]针对零担运输承运人合作提出一种加权相对节约模型(Weighted Relative Savings Model,WRSM)费用分配机制;Krajewska等[4]以夏普利值作为零担运输承运人合作的费用分配方案,用实际案例分析合作所能产生的结余;Yilmaz 等[5]分析了随机需求环境下,零担运输托运人之间的合作问题,并讨论了托运人合作的费用分配方案;曾银莲等[6]研究了合并运输策略下承运人之间的运输合作,分别讨论了基于时间的合并运输策略和基于数量的合并运输策略下承运人运输合作的费用分配问题。
以上研究大多是对同一阶段承运人之间的横向合作联盟进行研究,而高铁快递涉及不同运输阶段承运人之间的纵向合作,因此本文进一步借鉴供应链企业间纵向合作联盟的研究。在这方面Hill[7]和Zhou等[8]研究了供应链上下游企业的联合运作决策(包括联合生产/订货/定价)问题;Perea等[9]利用图论与合作博弈论讨论了由多个供应点、多个需求点与多个第三方中转点组成的三层分销供应链网络的合作问题;赵海霞等[10]基于链与链数量竞争及制造商的生产规模不经济环境,研究了纵向合作联盟的形成机制和利润分配合约的设计;Guardiola等[11]最早研究了一个供应商和n个零售商组成的横、纵向混合合作联盟运作问题,证明了非竞争性零售商横、纵向混合合作联盟合作博弈核的非空性,并设计了相应的收益分配解决方案;之后国内刘东升等[12]研究了多供应商与单一零售商组成混合合作联盟的可行性,并发现零售商加入供应商合作联盟组成大联盟,可以实现供应链的总体最优,同时给出了相应的收益分配方案;孙多青等[13]研究了一个制造商与多个零售商组成的逆向供应链合作联盟,给出了最优的收购定价策略,并利用改进的K-S方法设计了收益分配方案;肖旦等[14]研究了供应商与零售商之间横、纵向混合合作联盟的库存共享及合作联盟的稳定性问题,发现混合合作联盟的总期望利润高于零售商横向库存合作联盟。
这些研究对本文有很好的参考价值,但绝大部分供应链纵向合作联盟的文献都是研究各自独立的下游企业(不存在竞争关系)与上游企业间的合作,仅有文献[10]研究了两条供应链相互竞争环境下,各条供应链中企业的纵向合作问题,而高铁快递即为一个上游企业(高铁)与几个相互竞争的下游企业(快递)的纵向合作问题。另外,快递公司之间的服务水平差异是否会对纵向合作联盟产生影响,也是本文所要研究的问题。
1 问题描述与符号假设
本文研究高铁企业与两个竞争性快递公司在纵向合作联盟形成过程中的各方策略选择及博弈均衡,并分析服务水平差异对均衡结果的影响。两个快递公司之间由于公司实力不同存在服务水平的差异,同时两者在市场上进行数量竞争。快递公司和高铁企业可以选择合作与不合作两种策略。一旦双方选择合作则组成高铁快递纵向合作联盟,通过协同合作的方式提供快递服务,所得收益通过Nash讨价还价进行分配;若一方选择不合作,则不能形成合作联盟,快递公司会通过其他运输方式进行干线运输(本文假设通过公路运输,这也是目前快递干线运输的主要方式)并获取收益,而高铁则得不到任何收益。
合作与非合作两种模式比较:合作模式下,由于高铁在单位运输成本及运输时效性、稳定性上具有优势,该模式可以在提高快递服务的同时降低总成本,必然使快递公司在市场上更具竞争优势,但该模式下所得收益需要在快递与高铁之间进行分配;非合作模式下,快递公司通过其他方式进行干线运输,在运输成本和时效性上都不及合作模式,在市场竞争中必然处于劣势,但此时快递公司可以得到全部收益,而高铁却得不到收益。由于快递运输服务内容和客户需求的单一性,本文假设:
(1)两个快递公司所提供的服务除去服务水平差异外,其他各方面都是完全可替代的。
(2)运营中的其他成本,如快递派送成本,谈判成本等均为零。此外,由于两个快递公司存在服务水平差异,设快递1的服务水平较高,快递2的服务水平较低。
(3)以快递2的服务水平为基点(设为零),因为快递1的服务水平高于快递2,所以快递1的服务水平为正,由此反映了快递1与快递2服务水平的差异。
根据文献[15],将两快递公司的逆需求函数表示为:
(1)不与高铁合作时,p1=a-q1-q2+s,p2=a-q2-q1。
(2)与高铁合作时,p1=a+m-q1-q2+s,p2=a+m-q2-q1。
其中:a表示最高可行价格;s表示快递1的服务水平高于快递2的部分,即两快递公司的服务水平差异;m表示与高铁合作后快递速度和稳定性提升所带来的价格提升;p1,p2分别表示快递1和快递2的服务零售价格;q1,q2分别为快递1和快递2的市场需求;a,s,m,p1,p2,q1,q2均为正实数。
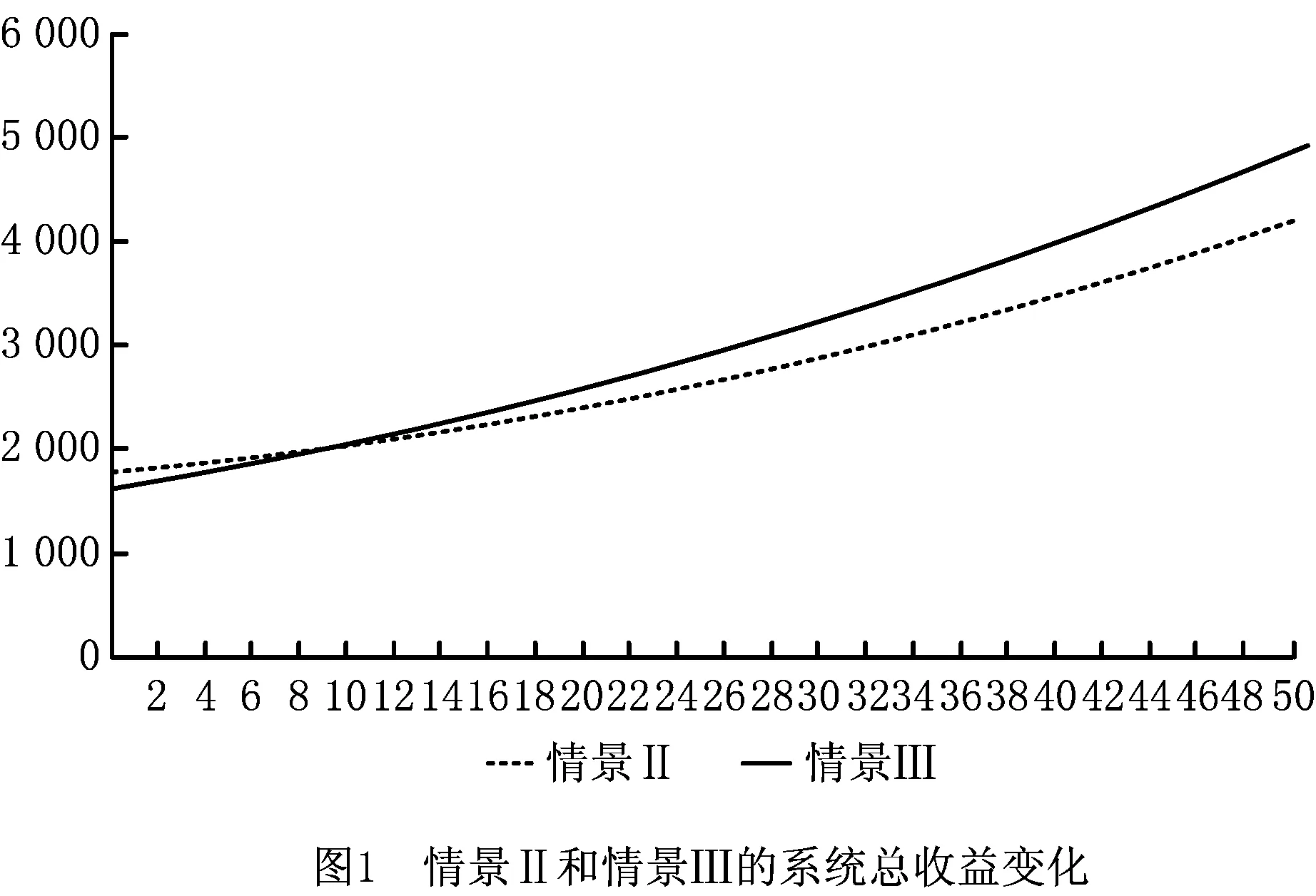
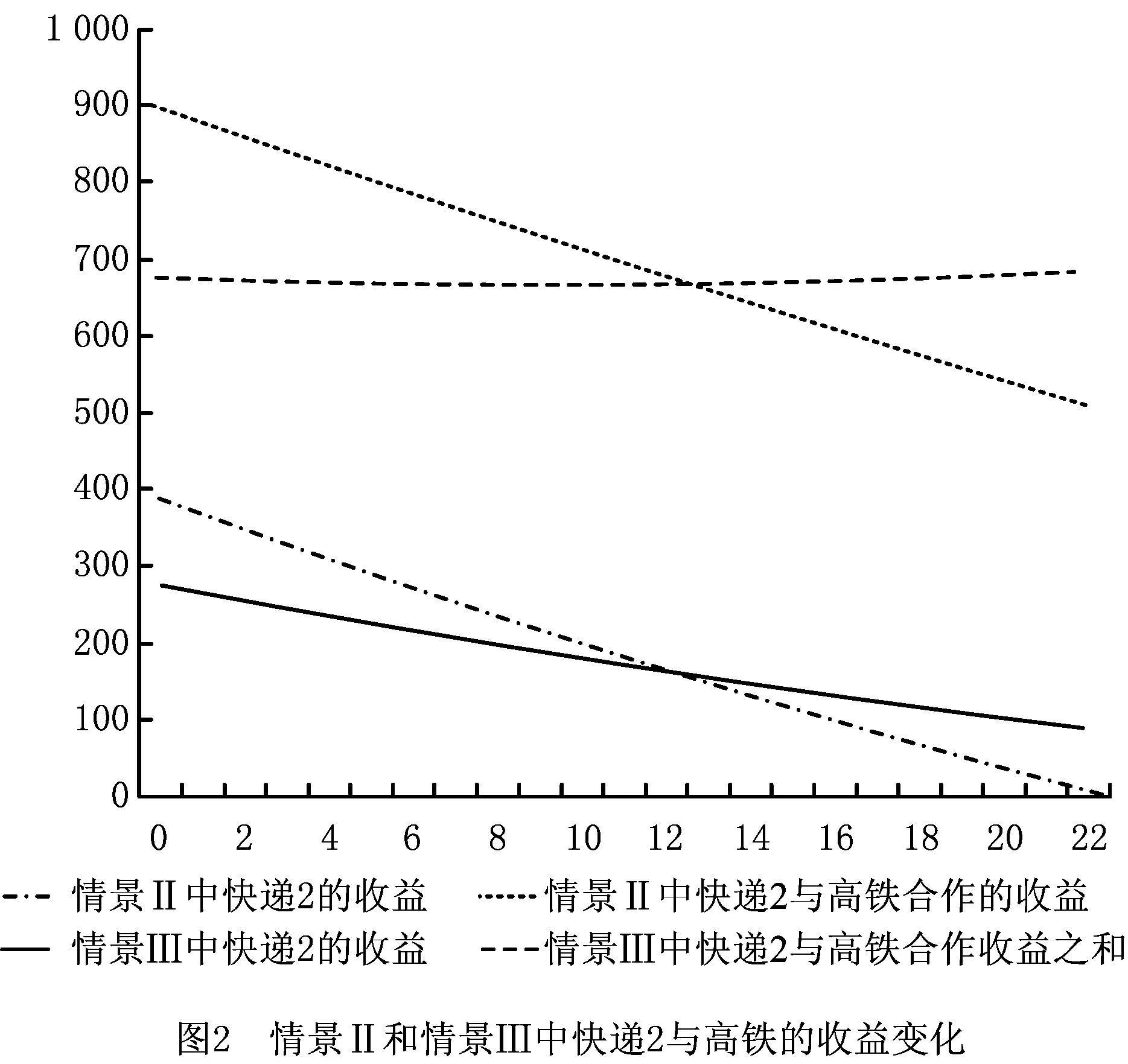
此外,用w表示快递公司通过公路进行干线运输的单位成本,c表示高铁运输的单位成本,且0 两个快递公司与高铁企业的纵向合作联盟存在4种可能的情景:①情景Ⅰ,即两个快递都不与高铁合作;②情景Ⅱ,即两个快递都与高铁合作;③情景Ⅲ,即快递1与高铁合作,快递2不与高铁合作;④情景Ⅳ,即快递1不与高铁合作,快递2与高铁合作。下面就这4种情景下的合作收益和各方收益进行分析。4种情景下的最大收益分别用上标Ⅰ,Ⅱ,Ⅲ,Ⅳ表示。 (1)情景Ⅰ:两快递都不与高铁合作 (2)情景Ⅱ:两快递都与高铁合作 (3)情景Ⅲ:快递1与高铁合作,快递2不与高铁合作 (4)情景Ⅳ:快递1不与高铁合作,快递2与高铁合作 (1)情景Ⅰ:两快递都不与高铁合作 (2)情景Ⅲ:快递1与高铁合作,快递2不与高铁合作 (3)情景Ⅳ:快递1不与高铁合作,快递2与高铁合作 (4)情景Ⅱ:两快递都与高铁合作 快递1的收益为 快递2的收益为 高铁的收益为 设高铁先后与两个快递公司进行谈判,可能存在两种谈判顺序,即先与1谈再与2谈(顺序a),或先与2谈再与1谈(顺序b)。将该博弈过程分为两个阶段:①第一阶段,高铁与其中一个快递公司谈判;②第二阶段,在第一阶段的谈判结果已知的情况下,高铁与另一个快递公司进行谈判。从高铁角度来看,若不合作则其收益为0,因此在快递1和快递2中,高铁至少要选择一个快递公司进行合作。不妨设顺序a和顺序b两种谈判顺序中,在面对第一个快递公司时高铁都会选择合作。 利用逆向归纳的思路对该博弈进行分析求解。先对谈判顺序a的情况进行分析。假设第一阶段快递1选择不合作,则第二阶段高铁与快递2双方的谈判结果与各方收益如表1所示。 表1 顺序a第一阶段不合作时第二阶段谈判的各方收益 若第一阶段快递1选择合作,则第二阶段高铁与快递2双方的谈判结果与各方收益如表2所示。 表2 顺序a第一阶段合作时第二阶段谈判的各方收益 下面分析快递1的策略选择。将第一阶段合作与不合作两种谈判结果下快递1的收益进行比较: 本章通过证明和数值实验方法,进一步分析服务水平差异对均衡结果的影响。 命题1随着s值的增大,情景Ⅱ和情景Ⅲ的系统总收益呈现加速增长,而且情景Ⅲ的增长速度大于情景Ⅱ。 证明将情景Ⅱ和情景Ⅲ的系统总收益分别对s求导,得到两条曲线的斜率: 可见,两条曲线的斜率均大于零,而且斜率随着s的增大而增大。因此,总体上,随着s值的增大,情景Ⅱ和情景Ⅲ的系统总收益都呈现加速增长的态势。将两者的斜率进行比较: 可见情景Ⅲ下,系统总收益的斜率始终大于情景Ⅱ,说明随着s值的增大,情景Ⅲ系统总收益的增长速度始终大于情景Ⅱ。证毕。 命题2随着s值的增大,情景Ⅱ下快递2的收益和情景Ⅲ下快递2的收益呈减速下降,而且情景Ⅱ的下降速度大于情景Ⅲ。 证明将情景Ⅱ和情景Ⅲ下快递2的收益分别对s求导,得到两条曲线的斜率: 可见两条曲线的斜率均小于零,而且斜率随着s的增大而增大。因此总体上,随着s值的增大,情景Ⅱ和情景Ⅲ下快递2的收益都呈现减速下降的趋势。将两者的斜率进行比较: 可见情景Ⅲ下,快递2收益的斜率始终大于情景Ⅱ,说明随着s值的增大,情景Ⅱ下快递2收益的下降速度大于情景Ⅲ。证毕。 证明情景Ⅱ的总收益减情景Ⅲ的总收益: 命题3说明,在快递1与高铁合作时,当s较小时快递2与高铁合作得到的系统总收益较大;而当s大于某一阈值时,双方不合作所带来的系统总收益反而更大。 证明情景Ⅱ中快递2与高铁的合作收益减去情景Ⅲ中快递2与高铁的收益之和: 本节在以上证明基础上进一步用更加直观的数值实验分析服务水平差异对均衡结果的影响,并解释造成这些影响的原因。 图1显示与命题1一致,随着s的增大,情景Ⅱ和情景Ⅲ的系统总收益都呈现加速增长的态势。因为s表示两快递公司的服务质量水平的差异,当s增大时,说明两快递公司实力上的差距在增大。也就是随着两快递公司实力差距的增大,系统总收益表现为逐渐加速增长的态势。这可以理解为,随着快递公司实力差距的扩大,实际上两者在市场上竞争的激烈程度在降低。竞争激烈程度的降低导致竞争所带来的系统内耗减小,从而导致系统的总体收益随之增长。同时,随着实力差距的进一步扩大,这种差距扩大,导致竞争激烈度的下降越来越明显,从而使系统总体收益呈现不断加速上升的态势。 此外图1还显示,在s较小时情景Ⅱ的系统总收益大于情景Ⅲ。随着s的增大,因为情景Ⅲ系统总收益的增速大于情景Ⅱ,所以当s大于某一阈值时,情景Ⅲ的系统总收益将超过情景Ⅱ,这一现象与命题3的表述一致。造成这种结果的原因在于情景Ⅱ中的两个快递公司都与高铁合作,而在情景Ⅲ中只有快递1与高铁合作,快递2不与高铁合作。因为与高铁合作可以降低成本,提高服务水平,所以在终端消费市场表现为情景Ⅱ下两快递的竞争激烈程度始终大于情景Ⅲ,即情景Ⅱ系统总收益的增速始终小于情景Ⅲ。当s较小甚至s=0时,因为情景Ⅱ中快递2与高铁的合作带来了系统总体收益的提升,所以此时情景Ⅱ的系统总收益大于情景Ⅲ。但随着s值的增大,情景Ⅱ系统总收益的增速始终小于情景Ⅲ,当s大于某一阈值时,情景Ⅲ的系统总收益必将超过情景Ⅱ,即当s值较大时,快递2与高铁不合作带来系统总收益反而更大。s变化对情景Ⅱ和情景Ⅲ中快递2与高铁收益的影响如图2所示 从图2可见,随着s值的增大,情景Ⅱ和情景Ⅲ中快递2的收益均减速下降,且情景Ⅱ中快递2收益的下降速度大于情景Ⅲ,这一现象符合命题2的结论。造成这种现象的原因在于,随着s的增大,两快递之间的实力差距逐步拉大。相对于实力强的快递1,快递2的实力越来越弱,因此其所能占到的市场份额和收益就逐步下降。同时,由于实力差距拉大导致竞争激烈程度逐渐下降,快递2收益下降的速度呈现逐步减小的态势。另外因为情景Ⅱ的竞争激烈程度始终大于情景Ⅲ,所以情景Ⅱ中快递2收益的下降速度大于情景Ⅲ。 图2还直观地验证了命题4及第3章给出的结论,即当s较小时,快递2与高铁合作(情景Ⅱ)获得的收益大于不合作(情景Ⅲ);但当s大于某一阈值时,选择不合作(情景Ⅲ)的收益反而大于合作(情景Ⅱ)。产生这一结果的原因在于,当s较小甚至s=0时,可以认为两个快递公司在市场竞争中势均力敌,无论谁与高铁合作都可以降低成本、提高服务质量,从而提升整体实力,在竞争中取得主动。因此在快递1已经与高铁合作的前提下,快递2选择与高铁合作可以保持自己原有的竞争地位,而且快递2与高铁的合作可以使双方总收益得到大幅提升,快递2必然选择合作。当s较大时,两快递公司的实力差距拉大,在竞争中实力悬殊,即便快递2选择与高铁合作也无法与快递1抗衡,反而使自己面临更大的竞争压力,而且随着s的增大,情景Ⅱ中快递2收益的下降速度始终大于情景Ⅲ;当s大于某一阈值时,快递2与高铁合作已经不能提升双方收益,反而会使双方收益下降。因此此时快递2不合作的收益一定会超越合作收益,即当两快递服务水平差距较大时,快递2选择不合作反而更优。 本文研究了两个存在服务水平差异且相互竞争的快递公司在与高铁组成纵向合作联盟开展高铁快递业务时,各方的策略选择及博弈均衡问题。首先,分析了三方合作可能出现的4种情景下的各方合作收益和各自收益;然后,将三方谈判的决策过程分为两个阶段,分析各方的策略选择和最终的博弈均衡;最后,在此基础上通过解析证明和数值实验两种方式分析了服务水平差异对博弈均衡结果的影响。通过研究得出以下结论:当快递公司间的服务水平差距较小时,会形成两个相互竞争的快递公司都与高铁组成纵向合作联盟的均衡状态;当快递公司间的服务水平差距较大时,会出现服务水平较高的快递公司与高铁组成合作联盟,服务水平较低的快递公司不与高铁合作的均衡状态。这一结果在一定程度上解释了目前高铁快递业务开展过程中,与高铁合作的均为服务水平较高、实力较强的快递公司这一现象。同时研究还发现,随着快递公司间服务水平差距的增大,两种均衡状态下的系统总收益均呈现加速增长的趋势,而低服务水平快递公司的收益均呈现减速下降的趋势,而且随着服务水平差异从零逐渐增加,先是第二种均衡状态的系统总收益超过第一种状态,然后才是第二种状态替代第一种状态达到新的均衡。 本文在纵向合作联盟收益分配时采用了Nash讨价还价模型,后续研究可以考虑使用其他收益分配方法;另外,本文未考虑信息不对称的情况,未来可以进一步在这方面进行拓展研究。 参考文献: [1] DAI Bo , CHEN Haoxun. A multi-agent and auction-based framework and approach for carrier collaboration[J]. Logistics Research,2011,3(2/3):101-120. [2] DAI Bo , CHEN Haoxun. Profit allocation mechanisms for carrier collaboration in pickup and delivery service[J]. Computers & Industrial Engineering,2012,62(2):633-643. [3] LIU Peng , WU Yaohua , XU Na. Allocating collaborative profit in less-than-truckload carrier alliance[J]. Journal of Service Science&Management,2010,3(1):143-149. [4] KRAJEWSKA M A, KOPFER H, LAPORTE G, et al. Horizontal cooperation among freight carriers:request allocation and profit sharing[J]. Journal of the Operational Research Society,2008,59(11):1483-1491. [5] YILMAZ O, SAVASANERIL S. Collaboration among small shippers in a transportation market[J]. European Journal of Operational Research,2012,218(2):408-415. [6] ZENG Yinlian, LI Jun, FENG Hairong. Collaboration in less-than-truckload transportation with stochastic demand[J]. Journal of Management Sciences in China,2015,18(7):48-58(in Chinese).[曾银莲,李 军,冯海荣.随机需求环境下零担货物运输合作[J].管理科学学报,2015,18(7):48-58.] [7] HILL R M. The optimal production and shipment policy for the single-vendor single buyer integrated production-inventory problem[J]. International Journal of Production Research,1999,37(11):2463-2475. [8] ZHOU Yongwu, WANG Shengdong. Optimal production and shipment models for a single-vendor-single-buyer integrated system[J]. European Journal of Operational Research,2007,180(1):309-328. [9] PEREA F, PUERTO J, FERNNDEZ F R. Modeling cooperation on a class of distribution problems[J]. European Journal of Operational Research,2009,198(3):726-733. [10] ZHAO Haixia, AI Xingzheng, TANG Xiaowo. Vertical alliance and profit sharing contract based on diseconomies of scale under chain-to-chain competition[J]. Journal of Management Sciences in China,2014,17(1):48-56(in Chinese).[赵海霞,艾兴政,唐小我.链与链基于规模不经济的纵向联盟和利润分享[J].管理科学学报,2014,17(1):48-56.] [11] GUARDIOLA L A, MECA A, TIMMER J. Cooperation and profit allocation in distribution chains[J]. Decision Support Systems,2007,44(1):17-27. [12] LIU Dongsheng, CHEN Guohua. Profits allocation research between multi-suppliers and single-retailer in suooly chain[J]. Operations Research and Management Science,2008,17(5):39-45(in Chinese).[刘东升,陈国华.供应链中多供应商与单零售商的利益分配问题研究[J].运筹与管理,2008,17(5):39-45.] [13] SUN Duoqing, MA Xiaoying. Pricing strategies and cooperative profit distribution based on game theory for reverse supply chains with multi-retailer participants[J]. Computer Integrated Manufacturing Systems,2012,18(4):867-874(in Chinese).[孙多青,马晓英.基于博弈论的多零售商参与下逆向供应链定价策略及利润分配[J].计算机集成制造系统,2012,18(4):867-874.] [14] XIAO Dan, ZHOU Yongwu. Stability of the inventory coalitions of manufacturer and retailers under quantity discount contract[J]. Operations Research and Management Science,2013,22(2):20-26(in Chinese).[肖 旦,周永务.数量折扣契约下制造商与零售商库存合作联盟的稳定性[J].运筹与管理,2013,22(2):20-26.] [15] CHENG H K, LI J, BAOZHUANG N, et al. Strategic analysis of dual sourcing under yield uncertainty in a co-opetitive supply chain[J]. Social Science Electronic Publishing,2015,6(8):34-58. [16] SHI Xiquan. Introduction to cooperative game theory[M]. Beijing:Peking University Press,2012(in Chinese).[施锡铨.合作博弈引论[M].北京:北京大学出版社,2012.]2 不同联盟情景下的收益分析
2.1 4种情景下的合作收益分析
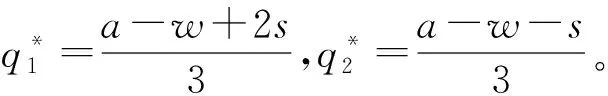
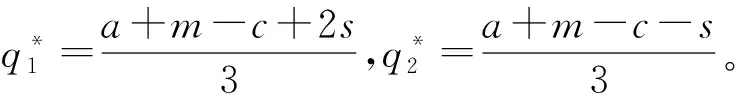
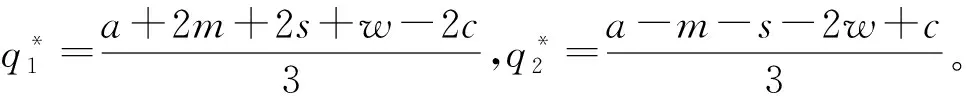
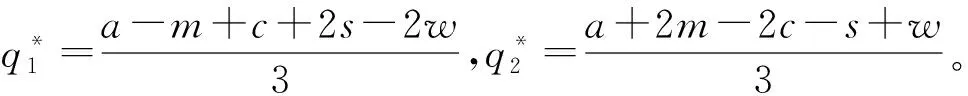
2.2 4种情景下的各方收益分析

3 各方的策略选择与博弈均衡

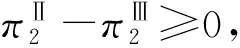
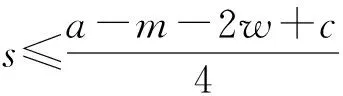
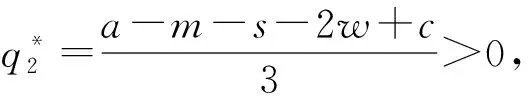
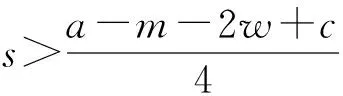
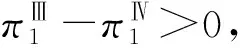
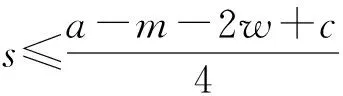
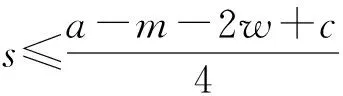
4 服务水平差异的影响分析
4.1 解析证明
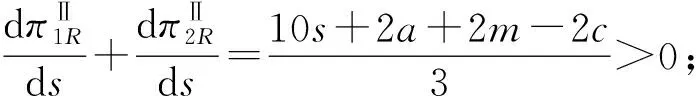
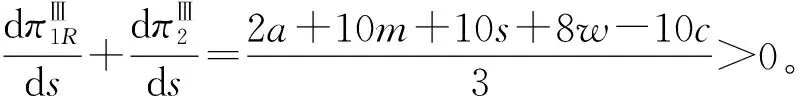
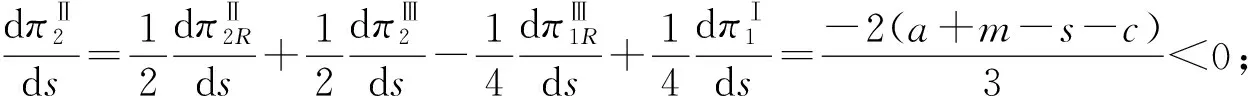
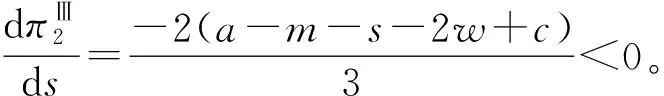
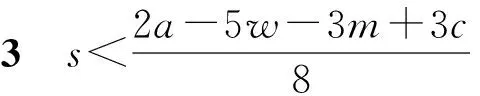
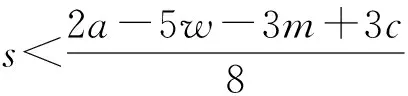
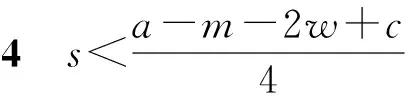

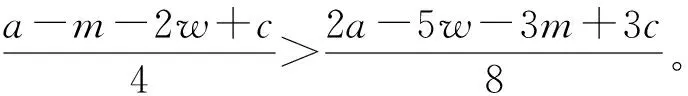
4.2 数值实验
5 结束语
