浅谈在规律探索教学中培养学生的思维能力

摘 要：小学数学中的“图形变化规律”“数列变化规律”和“操作活动变化规律”都是活动性、探索性比较强的“探索规律”内容，教师要在“数”“式”“形”的规律探索教学中，培养学生的思维能力。

关键词：探索规律；数学教学；思维能力

一切规律的探索，归根结底是方法的探索。探索规律是一个发现关系、发展思维的过程，有利于学生夯实基础，开拓创新，更能够体现数学思考过程，凸显过程与方法。同时，也能够让学生在自主探索与思考中感受到学习的快乐，形成积极的学习情感与态度。小学数学中的“图形变化规律”“数列变化规律”和“操作活动变化规律”都是活动性、探索性比较强的探索规律内容，教师要充分激活学生已有的知识经验，引导学生从不同角度探索规律，总结方法，让学生在探索规律的过程中培养思维能力。

一、在“数”的规律探索中培养学生的思维能力

小学低年段的规律探索内容大部分以“数”的规律探索为主。在探索数的规律时，我们首先应从题目所提供的数字入手，寻找不变的量；然后将所给的每个“数”化成有规律的式子，寻找变化的量；接着研究变化的量如何变化，归纳出规律，得出一般性的结论；最后，对于获得的结论，进行验算或证明它的正确性。通过探索“数”的规律，发展学生的合情推理能力。例如按规律填空：

（1）6、9、12、15、（ ）。

（2）12、5、14、5、16、5、18、5、（ ）、（ ）。

（3）5、21、10、19、15、17、（ ）、（ ）。

在解题时首先引导学生细心观察，采用或挨着找，或隔着找，或连着找的方法，我们不难发现（1）式的规律是后一个数等于前一个数加3；（2）式的规律是两数之间有一个固定数是5，而这两个相隔的数是越来越大的连续偶数；（3）式的规律是第一个相隔数是5的倍数，第二个相隔数是越来越小的连续奇数，从而得出（1）式的括号里应填18，（2）式的括号里应填20、5，（3）式的括号里应填20、15。当然不要忘了对所得出的规律的正确性进行验算。

二、在“式”的规律探索中培养学生的思维能力

小学中年段的规律探索内容大部分以“式”的规律探索为主，并安排为独立的学习内容。在探索“式”的规律时，教师首先引导学生观察有规律的代数式或等式；然后引导学生在这些有规律的式子中，寻找不變的量和变化的量，并研究变化的量如何变化，在实验、猜测的过程中找出规律，同时加以证明，并用字母表示。让学生经历观察、实验、猜想、证明等数学活动过程，培养学生的初步演绎推理能力。

例如，人教版四年级下册运算定律单元中的加法运算定律教学，原题是：李叔叔准备骑车旅行一个星期，今天上午骑了40km，下午骑了56km。李叔叔今天一共骑了多少千米？有的学生列式40+56=96，有的学生列式56+40=96，学生通过观察得出40+56=56+40。然后让学生再举出几个这样的例子，并进行大胆猜测：两个数相加，交换加数的位置，和不变。这个发现是否正确，需要我们去验证。接下来便要求学生举例验证：给大家30秒时间，你能写出几个就写几个，并把你举的例子和大家分享一下。同时启发思考：从我们举的例子来看，是否有交换两个加数的位置后，和会发生变化的？ 找不到反例，证明大家的猜想是正确的。最后，引导学生用自己喜欢的图形、符号、字母等代表两个加数，把加法交换律既简单又清楚地表示出来。

三、在“形”的规律探索中培养学生的思维能力

小学高年段的规律探索内容大部分以“形”的规律探索为主。主要类型有：形状一样但颜色不同的多个几何图形的图案问题，图形的折叠、旋转问题，同一种图形大小不一的排列问题，同一种图形的数量变化问题及数字与几何图形的有机结合排列等问题。此类规律通常以确定探索物体的个数和确定图形数量为主要内容出现的。

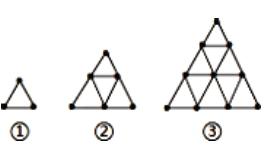
例如：用火柴棒按下面的方式搭图形，填写下表并回答问题：

①第n个图形的大三角形周长的火柴棒是几根？

②第n个图形的小三角形个数有几个？第200个图形的小三角形个数有几个？

图形编号 ① ② ③ ④

大三角形周长的火柴棒根数 3 6

小三角形个数 1

探索物体的个数时，可首先求出各图中物体的个数，然后将其与相应的图序数做对比，看两者有何关系，可得规律；或者求出各图中物体的个数后，问题的研究就由形转化成了数，只要研究数字规律即可得到图形规律。可知第①问的规律是：大三角形周长的火柴棒根数=图序数×3，所以第n个图形的大三角形周长的火柴棒是3n根；第②问的规律是：小三角形个数=图序数的平方，所以第n个图形的小三角形个数有n2个，第200个图形的小三角形个数有2200个。

总之，探索规律的学习应根据学生的年龄特征和数学知识发展的逻辑顺序，从一年级开始，由浅入深、循序渐进地进行安排，使学生在探索规律的过程中逐步提升思维，培养学生解决问题的探索性和灵活性。

作者简介：李鹏辉（1971— ），中小学一级教师，福建省农村骨干教师，龙岩市骨干教师，长汀县名师。