ZPW-2000轨道电路移频信号调制解调优化方法的研究
2018-06-29冯庆胜
冯庆胜,黄 朋
(大连交通大学,辽宁 大连 116028)
目前,我国的高速铁路行驶速度已高达350~400 km/h,速度之快,列车驾驶员很难看清地面上的信号机.因此列车的信号控制系统主要以机车信号为主,低速行驶时以地面信号灯为辅.我国在吸收法国UM71轨道电路优势的基础上,自主研制符合我国铁路运行环境的ZPW-2000系列轨道电路.
ZPW-2000系列无绝缘轨道电路系统是以铁路线路的两根钢轨为导体,两端加以电气绝缘或机械绝缘,并连接上发送和接受设备构成的电路.该轨道电路可以取消地面信号机,通过轨道电路提供连续、可靠的路况信息,实现车-地信息传输并将地面轨道信息通过线圈感应的方式传送到机车上,机车主机在接收到地面轨道电路设备发送的移频信号后,按照一定的方式转换为调制信号进行发送,经机车信号处理译码后可以获得相应的显示信息.因此司机可以完全的依赖机车信号进行驾驶[1].地面轨道电路设备发送的信号具有指定频率、相位、持续时间等参数的信息特征,这些指定的信息值可以由本轨道电路的状态决定,也可以按列车运行前方的一个或多个轨道电路的状态决定[2].信息的传输对信号的准确性及抗干扰能力要求相对较高,故应选择传输可靠性高、收敛速度快的信号处理方法.
总结传统的信号处理算法,并将这些算法的优缺点进行优化处理.采用复调制的细化快速傅立叶变换(ZFFT)算法和线性调频Z变换(CZT变换)对移频信号进行调制分析,用变步长的自适应滤波器(NLMS算法)对信号进行解调,进而满足用户信息需求.
1 ZFFT算法和CZT结合的移频信号的调制
由于ZPW-2000系列轨道电路中传输的是移频键控(移频)信号,载频、频偏、低频共同构成了移频信号的特征参数,信号机的显示是通过移频信号频率的参数传递控制信息.18种低频信号满足了列车多种速度信息的需要.ZFFT可以得到高精度的信号频率、幅值和相位等重要参数的数值.为保证信息的可靠传输,通过增大ZFFT细化倍数对干扰信号进行滤波处理,保留了有用信号的频谱.且对信号进行倍频分析和CZT在信号频谱局部细化方面的优势,通过两种算法的结合实现对低频信号的精确调制.
1.1 ZFFT变换的工作原理
ZPW-2000系列轨道移频信号属于相位连续的移频键控信号,利用低频频率调制载波.移频信号的波形如图1所示.

图1 移频信号的调制波形
在频率调制过程中,信号的数学表达式[3-4]为
(1)
(2)
式中:Afs为信号的振幅;fc为1 700 Hz;fp为11 Hz;φ0为0,sm(t)为低频调制信号;Td为调制信号的周期;fd为调制信号的频率;有fd=1/Td.对ZPW-2000轨道电路来说,信号的参数Afs、fc、fp、fd的取值[5-6]范围如表1所示.

表1 信号参数及参数指标
对低频信号sm(t)进行傅里叶变化得三角形式的傅里级数为
(3)
将f(t)展开成指数形式为
(4)
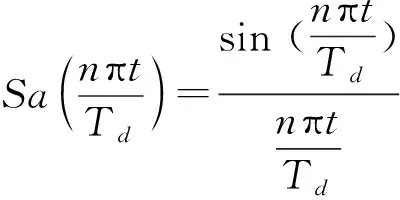
由式(3)可导出直流分量的相对幅度为
(5)
余弦分量的相对幅度为
(6)

图2 ZFFT处理过程
ZFFT是对经过傅里叶变换的低频频谱进行FFT变换,对感兴趣的频谱进行放大,进而对有用信号进行频谱变换,使信道得以充分利用.其主要处理过程如图2所示.图2中DLPF为数字低通滤波器,FFT为快速傅里叶变换.
由式(5)、式(6)分析可得,移频信号的频谱是以调制频率为间隔的谱线组成,谱线的能量越靠近fc±Δfp处越大,调制频率就越高,频谱分布的就越分散这种特点就更加有利于CZT算法分离出有用信号.
1.2 CZT变换的工作原理
频率调制和相位调制会产生与频谱搬移不同的新的频率成分,会干涉到有用信号的提取,因此通过CZT对已经调制的信号进行局部放大细化,来提高频率的分辨率[7-8].
CZT可以沿Z平面进行快速傅里叶变换,突破了传统快速傅里叶变换的序列长度的限制.选取低频信号的傅里叶变换级数为序列F(n)的CZT变换为
(7)
令
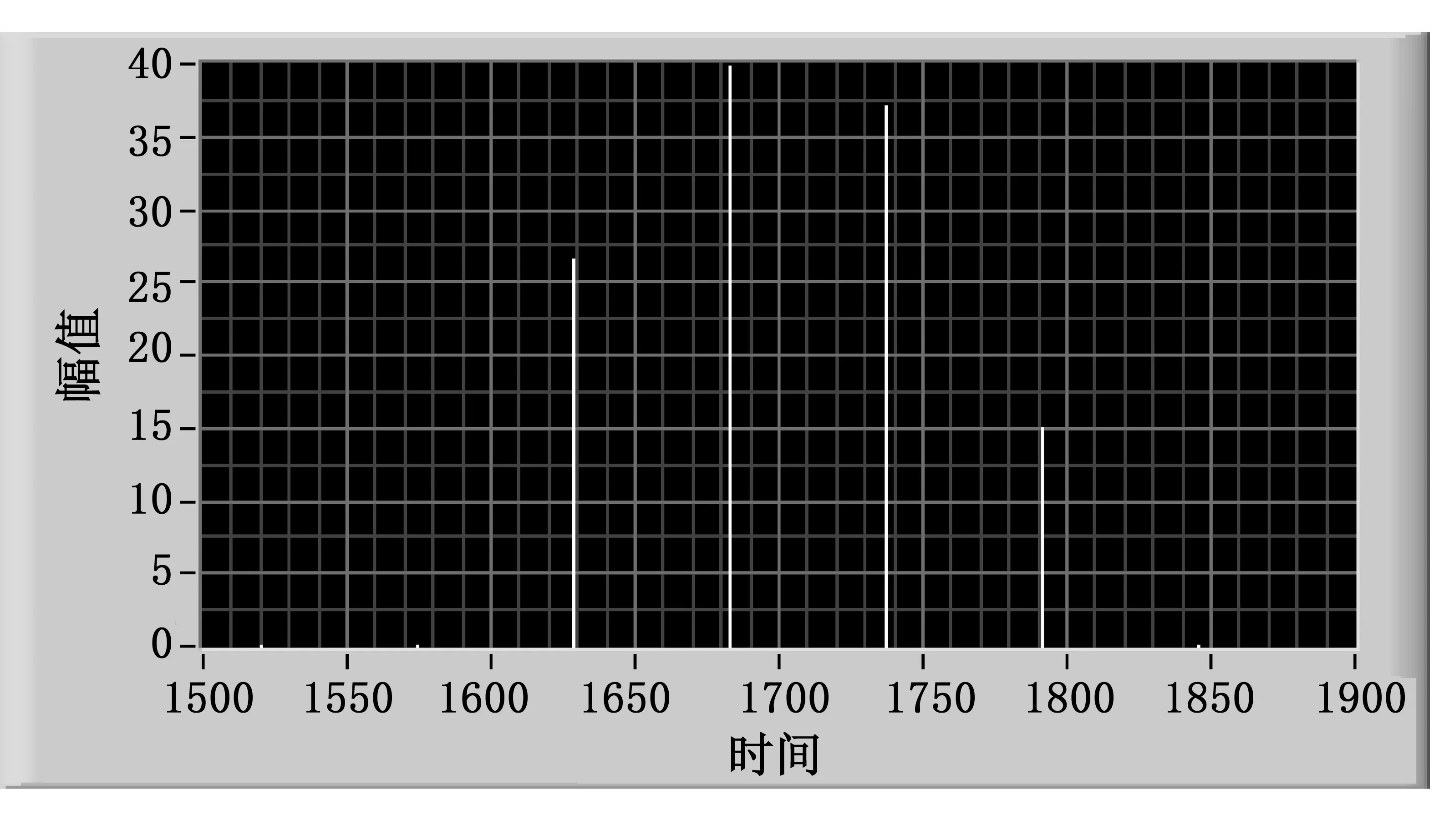
图3 移频信号的频谱
式中
A=A0ejθ0,
W=W0e-jφ0.
则
(8)
A0,W0为任意正数,若给定A0,W0,θ0,φ0,当r=0,1,2…∞时可得到一系列的点z0,z1,z2,…,zn,
对这些点取Z变换得
(9)
对低频信号10.3 Hz进行复制细化傅里叶变换后再对电信号的频谱进行CZT变换得到的仿真.则移频信号中频谱如图3所示.
该波形是以载频1 698.7 Hz,低频10.3 Hz进行调制的.低频信号的频谱是以新出现的频率f0为中心频率,其余谐波频率程逐渐衰减趋势.
通过这种方式来提高算法的分辨率,便于对有用低频信号进行窄带频谱分析.
2 基于NLMS算法的移频轨道信号的解调
移频信号解调的方法有鉴频法、差分检测法、过零检测法、自适应滤波法,考虑到移频轨道信号的窄带传输的特点,从而选用自适应滤波的方法对移频信号进行解调.自适应滤波器的滤波参数是随着外界信号变化而变化的,该滤波器的收敛需要经过一段时间的而自动调节,从而达到最佳的滤波效果.自适应滤波器是通过自适应算法最小均方误差(LMS)和递推最小二乘(RLS)两种最基本的算法实现滤波的,LMS是经典自适应滤波器.期待信号的迭代过程[9-10]为
d(n)=HT(n)x(n).
(10)
引入估计信号
y(n)=wT(n)+x(n).
(11)
由式(5)得输入向量
X(n)=[x(n),x(n+1)…x(n-L+1)]T,
(12)
冲击响应向量HT(n)=[h0(n),h1(n),…,hL-1(n)]T,
自适应滤波器的系数向量为w(n)=[w0(n),w1(n),…,wL-1(n)]T[11].
误差信号为
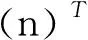
(13)
由最速下降法得
w(n+1)=w(n)+μ[-J(n)]=w(n)+2μx(n)e(n).
(14)
n=1,2,3…为时间序列;x(n)为n时刻的输入信号;e(n)为n时刻的信号误差,μ为步长因子,是控制滤波器稳定性和收敛速度的参量.由式(11)迭代公式可以看出LMS算法收敛速度取决于μ的取值[11-12],且
(15)
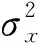
AW(n+1)=w(n+1)-w(n).
(16)
滤波器在新的权向量下得到的约束条件是
wT(n+1)x(n)=d(n).
(17)
AW(n+1)的范数平方为
‖aw(n+l)‖2=[w(n+1)-w(n)]T[w(n+1)-w(n)].
(18)
以欧式范数的平方作为目标函数,用拉格朗日求目标函数的最小值,令
f(n)=‖aw(n+l)‖2+b[d(n)-wT(n+1)x(n)],
(19)
式中b为拉格朗日系数.
式(17)两端对w(n+1)求导得
=2[w(n+1)-w(n)]-bx(n).
(20)
令式(19)为零,可得更新权系数公式
(21)
将式(21)代入式(14)中可以得到
即
将NLMS算法的更新公式与LMS算法的更新比较可得前者的收敛速度更快且稳定性很高,可以实现移频信号的实时传送.
3 仿真结果
通过Lab VIEW模拟仿真[13]对移频信号采用上述算法进行调制解调,低频信号经快速傅里叶变换的频谱.当频率大于50 Hz时的功率信号都是衰减的,有效遏制了在信道中对有用信号的干扰[14].程序的属性设置采样频率为50 Hz,采样频率和采样数均为1 000,低频信号经过NLMS算法的解调结果如图4所示.在经过变步长的自适应滤波器处理后,已经恢复调制信号的波形,且失真程度较小,该方法精度很高,误差在信号的允许范围内.
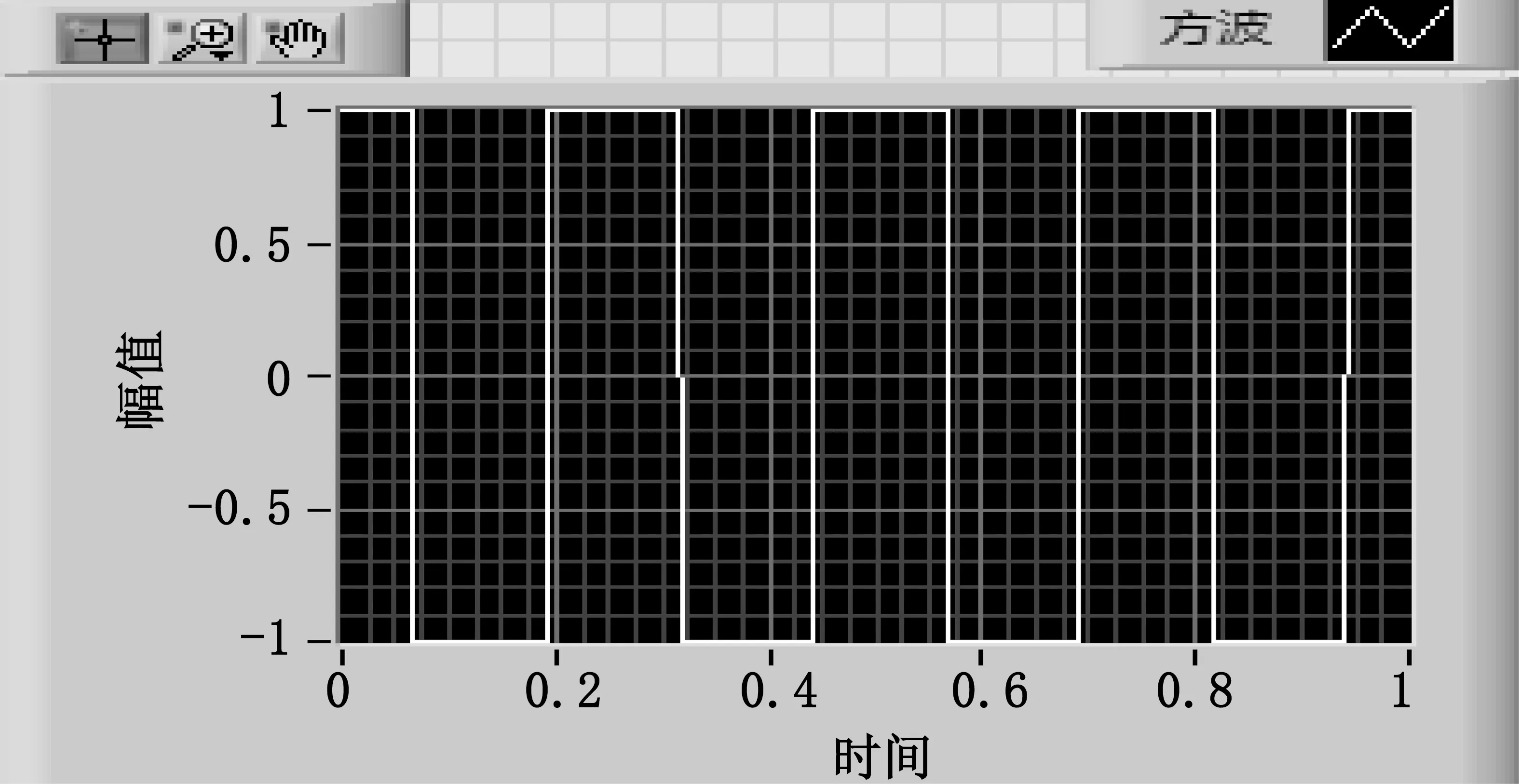
图4 低频信号
4 结语
为保证移频信号的可靠传输,采用复调制细化的快速傅立叶和线性Z变换算法,改变移频信号的频谱大小,增加采样点数,降低带宽.经变步长自适应滤波器处理得到低频信号的波形.这些算法也曾应用在一些机械设备、医疗器械上,其使用效果和认可度相对较高.模拟仿真实验结果表明此算法是可行的.
参考文献:
[1] 林瑜筠.区间信号自动控制[M].北京:中国铁道出版社,2015:98-113.
[2] 唐涛.列车运行控制系统[M].北京:中国铁道出版社,2012:52-60.
[3] 中国铁路总公司.列控车载设备典型故障案例[M].北京:中国铁道出版社,2013:51-55.
[4] 丁康,潘成灏,李巍华.ZFFT与Chrip-Z变换细化选带的频谱分析对比[J].振动与冲击,2006,25(6):9-12.
[5] 郑君里.信号与系统(上册)[M].北京:高等教育出版社,2013:102-127.
[6] 刘杰.移频轨道电路参数测试及信号处理技术的研究[D].哈尔滨:哈尔滨理工大学,2003.
[7] 樊昌信,曹丽娜.通信原理[M].北京:国防工业出版社,2012:104-107.
[8] 李国庆,武晓春.基于复调制的ZFFT算法在轨道电路信号检测中的应用[J].计算机测量与控制,2016,24(1):262-265.
[9] 曹亚丽.自适应滤波器中LMS算法的应用[J].仪器与仪表学报,2008,26(8):452-454.
[10] 卢炳乾,冯存前,龙戈农.一种基于正弦函数的归一化变步长LMS算法[J].无线电工程,2014,44(3):21-23.
[11] 孔德龙,王瑞峰,包超峰.NLMS算法在轨道电路信号解调中的应用[J].科学技术与工程,2014,14(4):61-65.
[12] 安义岩.便携式轨道移频信号检测仪的研发[D].太原:太原理工大学,2016.
[13] 夏晓明.基于Lab VIEW的轨道电路信号处理研究[D].成都:西南交通大学,2012.
[14] 周鹏.精通Lab VIEW信号处理[M].北京:清华大学出版社,2013:145-157.
