模糊聚类分析在液压油性能评价中的运用

刘金平，杨勇辉

(中国地质大学 机械与电子工程学院，湖北 武汉 430074)

液压系统是工程机械重要的组成部件，在工程机械功能发挥上起到关键作用.液压传动最大的特点是在瞬间能产生很大的力和力矩，这对于工程机械或短时需要巨大能能量的设备而言是一种最为合适的选择.液压系统另一个用途是机械传递，液压传动突出的特点是运动灵活，能实现多种运动并在不同的运动方式中快速转换，正好能满足自动半自动控制运动复杂、启动频繁、运动敏捷的要求，在各类机床中广泛使用.此外液压传动还有运动平稳、可实现无级变速、过载保护、体积小、质量轻等优点，在现代装备中也得到了大量使用[1-2].液压油是液压传动的主要传递介质和重要组成元素，它的性能直接影响液压系统的可靠性、安全性、功能和效率，同时也影响系统的使用寿命和维护成本，因而科学判断液压油的性能，对用户正确选择产品，维护液压系统的高效、可靠、安全运行具有重要的现实意义.虽然国家对各类液压油质量制定了有关的标准，但它仅能用于判定产品合格与不合格两类状况，无法更进一步地细化其质量，就市场化而言，难以体现“优质优价，以质论价”的商品交易原则.液压油评价方法较多，但都是粗线条式的[3-8]，合格产品也有质量的差别，无法真正衡量其合格程度.模糊聚类分析是一种智能化信息处理的重要算法，是利用模糊数学理论来研究聚类问题的一种数据分类方法，具有优良的聚类性能，能根据实际情况调整分类的形式.聚类随需要动态变化，分析方法逻辑严明、条理清晰，过程简便，易于理解，结果直观，适应性强.本文应用模糊聚类分析方法评定液压油质量，能精确细划液压油的质量，对提升液压油商品化价值，防止以次充好，维护消费者利益等具有积极意义.

1 模糊聚类分析的基本方法

1.1 模糊聚类原理

数据的聚类分析是根据数据系列的特征按照某种特定的要求或规律对其进行分类的一种数据分析方法.简单讲，就是在一组数据中将特征类似的数据集合在一起，归为一类，使整个数据族分为不同特征的若干组别.数据聚类的原则是：使得各类之间的数据差别尽可能大，类内之间的数据差别尽可能小，即为“最小化类间相似性，最大化类内相似性”原则[3-4].在现实生活中，我们遇到的许多数据往往具有模糊性，因此，对这类带有模糊性的数据进行聚类分析，不仅要考虑数据之间是否存在关系，还要更进一步考虑它们之间关系的紧密程度.因此，运用模糊数学工具解决这类问题更加合适，模糊聚类分析便是使用模糊数学的方法处理聚类分析的过程.模糊聚类基本原理就是将一个没有类别标记的杂乱样本集，按照某种相似关系将其划分为若干个子集(类)，使相似程度较高的样本尽量划归于同一类，而不相似或者相似程度低的样本尽量划到不同的类别之中.

1.2 确定评价指标

液压油用途广泛，种类繁多，性能技术指标较多，不同种类和不同用途对其性能要求有所差异和侧重[9]，在液压油性能评价指标上，既要体现全面性、系统性原则，也要体现一般性、代表性原则，同时还要兼顾可操作性、可量化性的原则.液压油的基本要求是良好的流动性、稳定性和较长的使用寿命.基于上述原则，本文提出了评价液压油性能的8个指标，具体如图1所示.

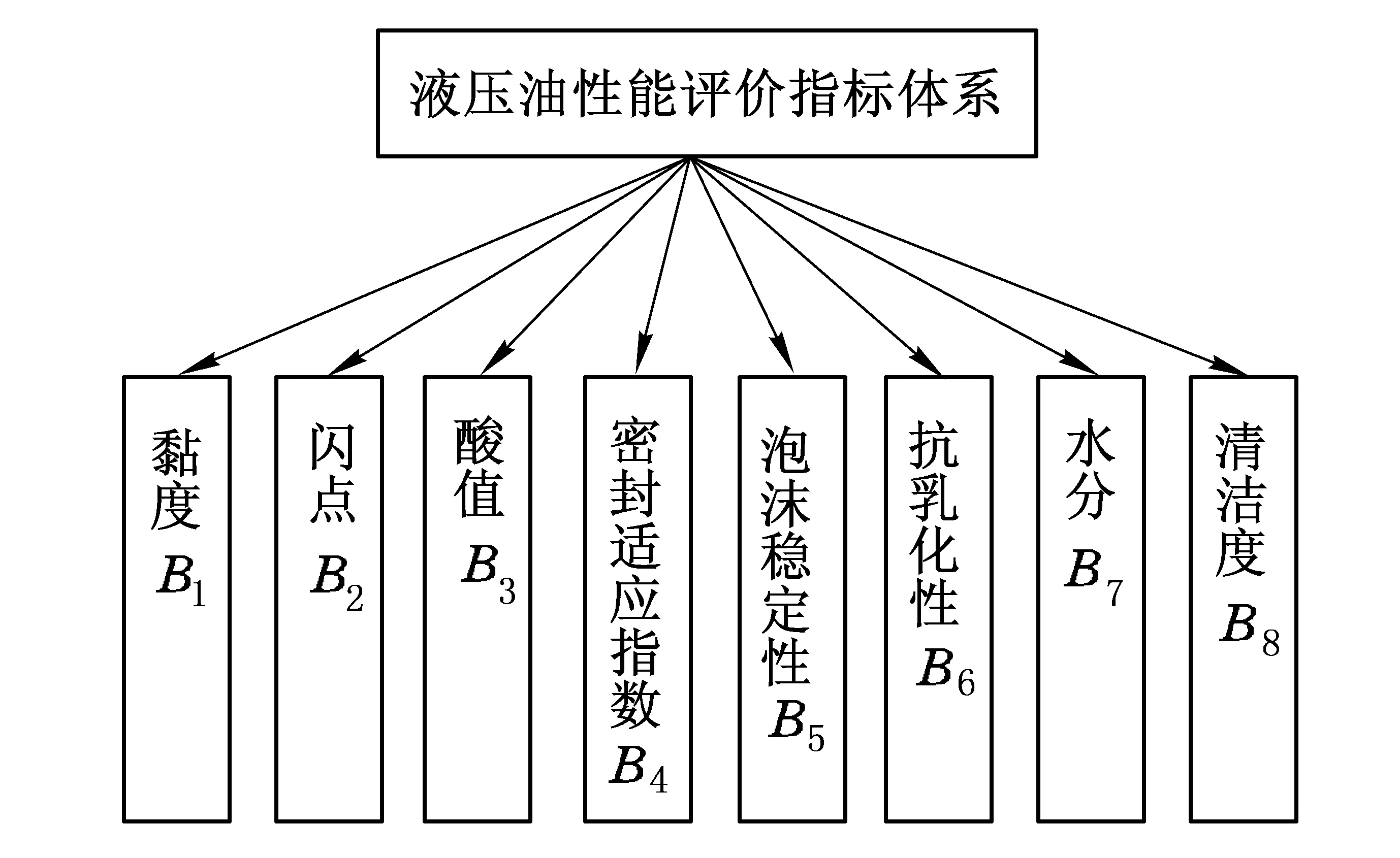
图1 液压油性能评价指标体系

1.3 数据标准化

由于液压油质量指标的量纲和数量级不尽相同，为了方便比较，需要对原始数据进行标准化处理.为了使模糊聚类分析的效果更好，标准化通常分两步进行：1)平移—标准差变换；2)极差变换—归一化[10-12].

平移—标准差变换公式为

(1)

(2)

(3)

式中：rij为原始数据，xij为平移标准差变换后的数据，μj为第j个指标的均值，σj为第j个指标的标准差.

原始数据经过第1步变换后，每个指标数据的均值为0，标准差为1.平移—标准差变换虽然消除了指标数据的量纲的影响，但是数据并不一定在 [0，1]区间上，因此，还须对其进行极差变换—归一化处理，公式为

(4)

式中yij为归一化后的数据.

原始数据通过两步归一化后，不仅消除了评价指标的量纲不同对聚类效果的影响，而且生成的数据都在区间[0，1]中，即指标的评价值都转化为模糊数的形式，这样就为模糊聚类创造了条件.

1.4 确定指标的权重

由于属性指标的权重对聚类的结果影响较小，故本文采用较为简单的环比评分法确定评价指标的权重.首先根据评价指标对评价结果的影响大小，对每个评价对象的重要性程度进行评分，可采用百分制或十分制，可为小数也可为分数，根据决策者的喜好自行决定.设第j个评价指标的重要性评分为Pj，则其权重为

(5)

式中：wj为第j个评价指标的权重(j=1，2，…，m)， ∑wj=1.

1.5 计算加权规范化数据

权重确定后，就可对规范化数据进行加权处理，将规范化数据转变为加权规范化数据，即

zij=wj·xij，

(6)

式中：zij为第i个评价对象第j个指标的加权模糊数，wj为第j个指标的权重.

1.6 构造模糊相似矩阵

模糊聚类分析的核心是建立模糊关系矩阵.模糊关系矩阵通常以模糊相似矩阵体现，它反映的是各评价对象的相似程度，是模糊聚类分析的基础.构建模糊相似矩阵方法较多，一般须要满足3个原则：1)正确性；2)不变性；3)可区分性.其中，最大最小法是构建模糊相似矩阵诸多方法中较为理想和有效的一种，不仅满足上述3条原则，且分辨率很高，判断准确.故本文采用最大最小法来构建模糊相似矩阵，它由各评价对象间的相似系数构成，即R=(rij)n×n，根据最大最小法法则，评价对象之间的相似系数[11-12]计算公式为

(7)

式中：rij表示样本xi与xj之间的相似程度，rij的值越大，表明这两个样本相似程度越高；rij=1表明两个样本完全相同；rij=0表明两个样本完全不同.

各评价对象相似系数求出后，即可得模糊相似矩阵.显然，模糊相似矩阵为对称矩阵：

1.7 聚类

模糊聚类分析中要求建立的模糊关系矩阵为模糊等价矩阵，它必须满足自反性、对称性和传递性3种要求，而模糊相似矩阵虽然具有自反性、对称性，但不一定具有传递性，即不一定为模糊等价矩阵，因此，还需要采取一定方法将模糊相似矩阵R转化成模糊等价矩阵.将模糊相似矩阵转化为模糊等价矩阵的方法比较多，最简捷的方法是采用二次法求传递闭包t(R)方式，即以模糊相似矩阵R为基础，依次求模糊相似矩阵的2次方、4次方、…、k次方(k必须为偶数)，当首次出现Rk·Rk=Rk时，Rk即为传递闭包t(R)，t(R)即为所求的模糊等价矩阵.具体过程如下：

R→R2→R4，…，→R2k=R2(k+1)=t(R) .

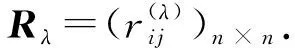
(8)

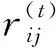
可见，截矩阵中的元素只有0或1，这便于进行识别和分类.根据截矩阵Rλ中元素的分布情况进行分类，元素相同的行划归一类，λ从大到小依次取不同值，得到相应的分类结果，从而实现动态聚类.

1.8 确定最佳分类数

在模糊聚类分析中，聚类方式是随阈值变化而变化的，阈值λ取不同的值，得到的分类结果就不同，即动态聚类，它只是作为一种聚类方式研究之用，其实用意义不大.而在解决实际问题时，往往需要确定一个确切的分类结果，即确定最佳分类数r和阈值λ，二者实际上属于一个问题，它们是一一对应的，最佳分类数确定后最佳阈值也就确定了.最佳分类数r通常采用统计量F来确定，最佳阈值λ则通过最佳分类数r获得.

1)计算原始数据矩阵总体样本的中心向量

(9)

2) 计算各类别样本的中心向量

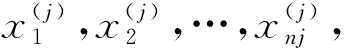
(10)

由此引入统计量F

(11)

(12)

(13)

统计量F是描述分类有效性的一个指标，其意义可从两个方面概括，统计量F的分子含义是表示类与类之间的距离，分母则表示类内样本之间的距离.类与类之间的距离越大，类内样本之间的距离越小，表明分类越显著.故F值越大，表明类与类之间的距离大，显示各类的差别越大，同时也说明各类内部元素之间的距离越小，即同类元素之间的差距越小，这也就意味着分类效果越好.具体而言，如果F>F0.05(r-1，n-r)，则说明类与类之间差异是有统计学意义的，分类是比较合理的.如果满足条件F>F0.05(r-1，n-r)的分类数目不止1个，则需要进一步考察ΔF=(F-F0.05)/F0.05值的大小，选取ΔF最大的对应分类数为最佳分类数目.

2 实例分析

文中以L-HL32普通液压油为例，取样10个不同厂家生产的该牌号的液压油，选取图1所示的8个指标作为其质量评价指标.故评价对象集为S={s1，s2，…，s10}，评价指标集为C={c1，c2，…，c8}，所有指标性能测试参照国家相关标准，经检测，这10个样品的8个指标值见表1(数据为测试3次的平均值).

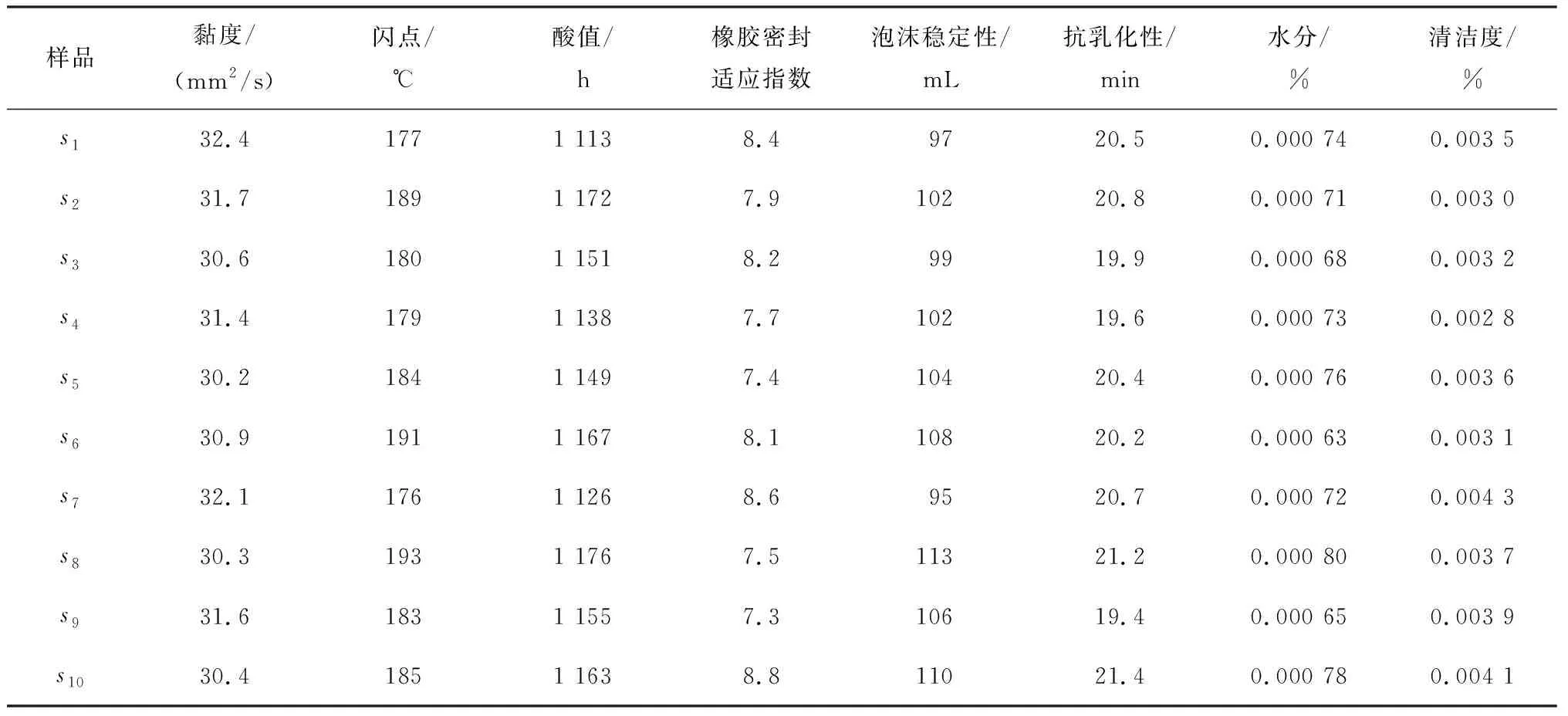
表1 液压油性能测试值

按式(1)～式(4)对原始数据进行规范化处理，结果见表2.

确定指标权重.根据生产实际经验，取液压油8个评价指标的重要性评分分别为：P1=10.0，P2=9.5，P3=9.0，P4=8.5，P5=8.0，P6=7.5，P7=7.0，P7=6.5.

则它们的权重分别为：w1=0.151 5，w2=0.143 9，w3=0.136 4，w4=0.128 8，w5=0.121 2，w6=0.113 6，w7=0.106 4，w8=0.098 5.

按式(6)计算加权规范化数据，结果见表3.

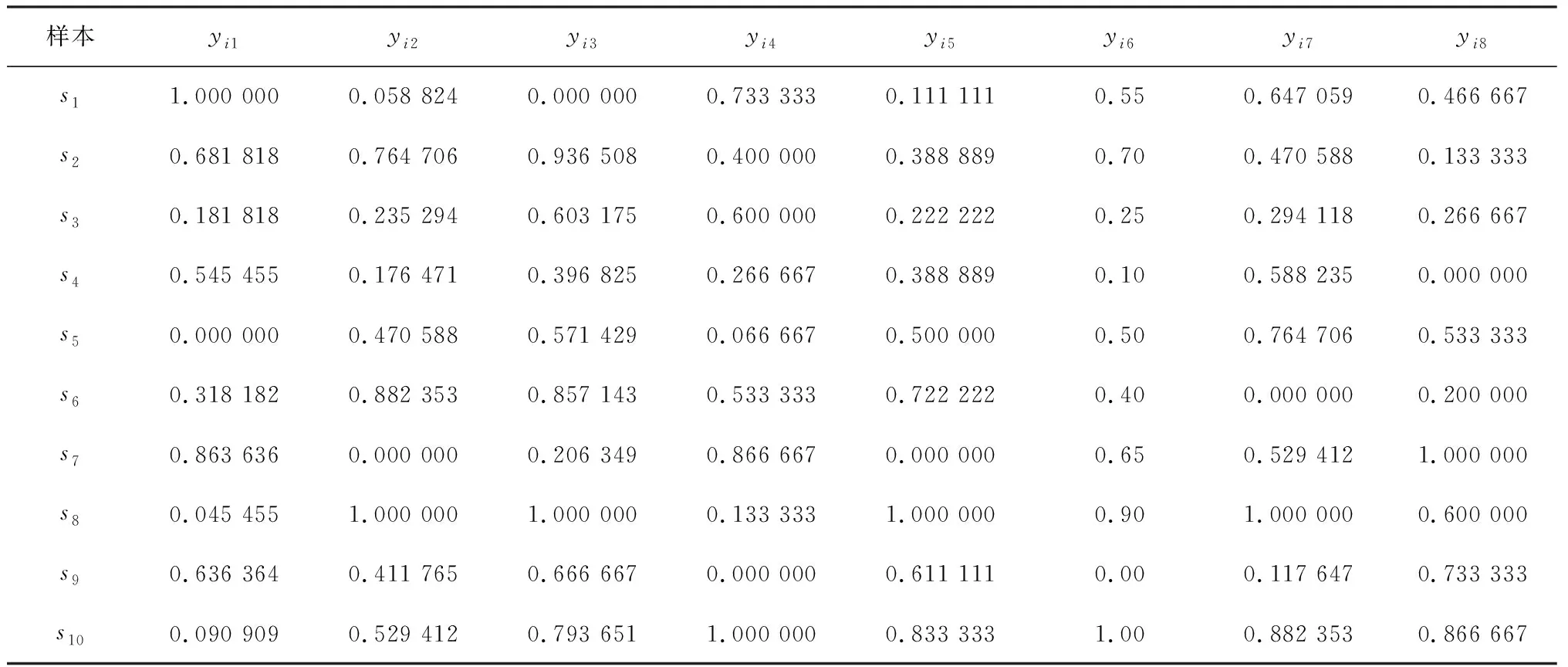
表2 原始数据规范化结果

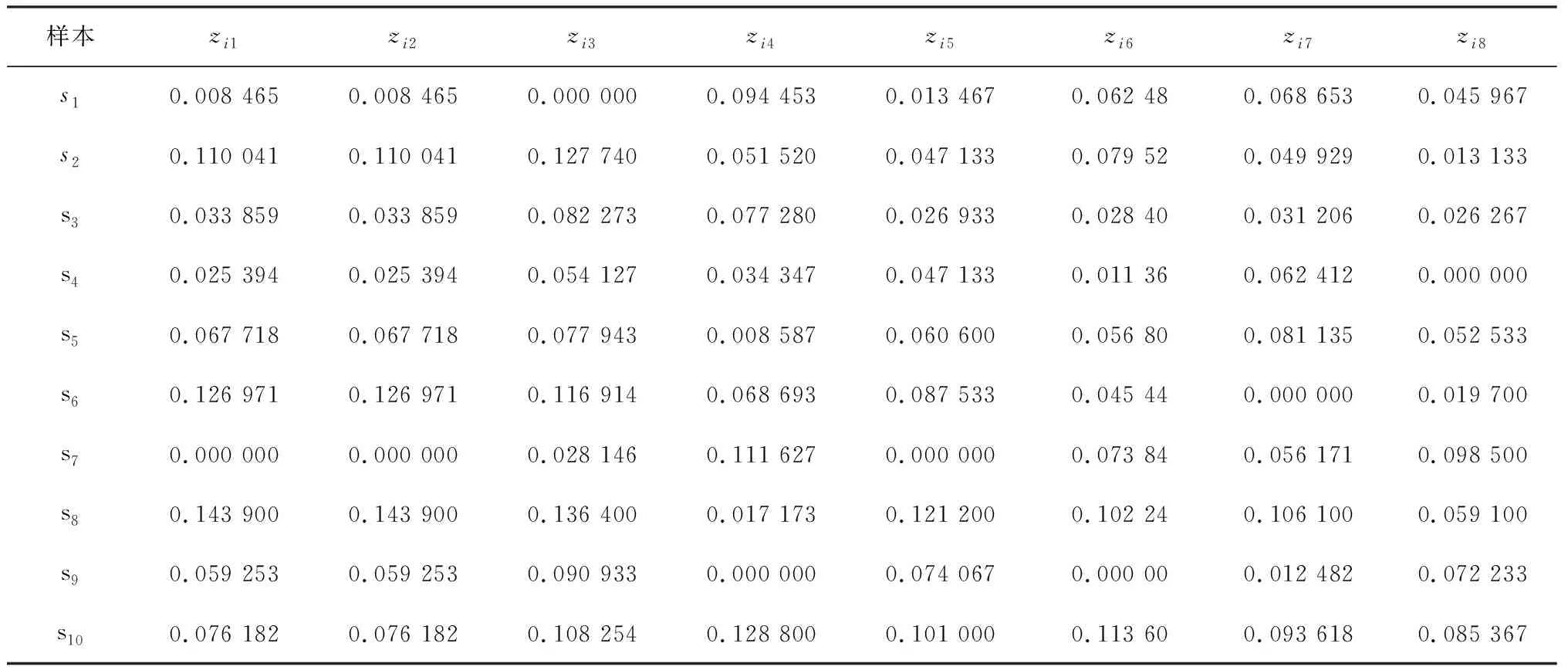
表3 加权数据规范化结果

按式(7)计算评价对象的相似度，得到相似矩阵R

计算相似矩阵R的传递闭包，得到模糊等价矩阵t(R)

根据传递闭包t(R)得到分类阈值

Lλ=[0.446092，0.489057，0.533258，0.604127，0.620320，0.630094，0.641760，0.647168，0.719333，1].

根据阈值Lλ对样品进行动态聚类，结果见表4.同时得到动态聚类图，如图2所示.

表4 动态聚类结果

图2 液压油动态聚类图

对于样本分类问题，确定最佳分类数目十分关键.分类数目应当合适与恰当，分类太少，无法体现个性之间的差异性，也就失去了研究它们的必要；分类太多，信息杂乱，理不清头绪，也就无从分析个体之间的联系.因此，对10个大小的样本来说，一般分为3～5类比较合适.

当r=3时，统计量F=1.527 3，F0.05(2，7)=4.74，F

当r=4时，统计量F=4.782 6，F0.05(3，6)=4.76，F>F0.05(3，6)，分类效果显著.

当r=5时，统计量F=1.187 9，F0.05(4，5)=6.26，F

因为只有当r=4时，分类效果才显著，因此，最佳分类数为4，对应的分类阈值λ=0.604 127，样本组成为：{s1、s7}，{s3、s4}，{s5、s9}，{s2、s6、s8、s10}.

3 结语

液压系统是机械设备的重要组成部分，其性能与液压油的性能有很大关系，为了保证液压系统的可靠性和安全性，不仅需要掌握液压油的大体质量，而且还要详细了解其质量优劣程度.模糊聚类分析是对模糊事物按一定要求进行分类的一种数学分析方法，它能客观准确反映数据样本之间的内在联系，具有通俗易懂、易于实现、应用范围广、决策形象直观、结论简明等诸多优点，在许多工程领域中得到了广泛应用.本文运用模糊聚类理论，采用极大极小法构成相似矩阵，对液压油质量进行了分类，更进一步细化了液压油质量评判尺度，对用户选择液压油产品具有指导意义.

参考文献：

[1] 周涛,郭静英,赵志龙,等.液压油多参量品质诊断研究[J].液压与气动,2017,41(10):23-25.

[2] 曾萍,杨智渊,汪必耀,等.航空液压油标准体系概述和性能评估方法研究[J].机床与液压,2018,47(1):18-20.

[3] 薛飞,陈炳耀,杨善杰.多级液压油性能影响因素的探究[J].化工管理,2017,24(9):43-44.

[4] 王月行,朱伟伟,郑东东,等.基于氧化耐久性台架液压油模糊综合评价[J].润滑与密封,2018,43(1):51-53.

[5] 刘多强,王德岩,刘爱全.合成烃低温抗燃液压油润滑性能的评价[J].合成润滑材料,2016,22(4):32-35.

[6] 程安国,陈惠卿,汤涛.基于层次分析法综合评价液压油的性能[J].液压气动与密封,2015,27(4):49-52.

[7] 陈世明,王强,赵玮,等.多层次模糊综合评判法在液压油性能评价中的应用[J].机械研究与应用2009(4):63-65.

[8] 赵辉,冯永保,李淑智,等.液压油性能评价的两种方法及改进措施研究[J].矿山机械,2016,44(2):72-73.

[9] 王祖安.液压油的性能特点及选用原则[J].石油商技,1998(5):54-59.

[10] 吴楠.加权模糊聚类在第三方逆向物流供应商选择中的应用[J].现代物业,2010,9(10):33-35.

[11] 舒服华.模糊聚类分析在饲料加工质量评价中的应用[J].饲料广角,2016(22):40-43.

[12] 王艳.模糊聚类分析在大理石质量评价中的应用[J].石材,2017(8):40-46.