最优货币区中的劳动力流动——基于福建自贸区金融风险防范的视角

吴孔磊

（福建师范大学，福建福州350108）

一、引 言

自由贸易区（Free Trade Zone），可被看成是一个小型的货币区。福建自贸区成立后，如何发展它和如何防范相关金融风险，涉及到劳动力的流动问题。

本文将主要以最优货币区为背景，以劳动力流动为主轴，以工资、价格和偏好为主要因素，以福建自贸区金融风险防范为归宿，求解社会最优化和最优劳动力流动。在此基础上，最优的政府干预政策、与自由贸易区金融风险防范相关的人口、就业和劳动力流动等一系列问题，也就便于寻找到答案。

在借鉴 Friedman（1953）、Meade（1957）和 Scitovsky（1958）有关弹性汇率机制、自由贸易区和其它相关经济理论的基础上，Mundell（1961）赞赏劳动力流动作为最优货币区（Optimal Currency Area， OCA）的一个前提。 Mundell（1961）的这一观点，已经成为最优货币区的文献研究的一个基石。其研究强调：来自于劳动力流动的宏观溢出收益并不明显；经济开放性的程度是一个重要的参数。McKinnon（1963）认为，开放性是最优货币区的另外一个前提。Farhi and Werning（2014）也对宏观溢出收益和开放性作了一些讨论。

我们认为，最能模拟当前有关自由贸易区（用“最优货币区”代替）劳动力流动的模型是Farhi and Werning（2014）的模型。Farhi and Werning假设：价格是既定的；偏好是一致的；市场或产品都是完全竞争的；工资和价格存在着刚性或黏性的问题。其结论对政策也有一定促进作用。但是，我国的二元制户籍制度还存在，劳动力很难自由流动并完全地享有当地居民的同等待遇；并非所有市场和产品都是完全竞争的；工资与价格也可双弹性变化；偏好也并非都是一致不变的。

我们在 Mundell（1961）和 Farhi and Werning（2014）理论的基础上，考虑劳动力的不自由流动，价格的可变性，偏好的非一致性，市场或产品的非完全竞争性，工资和价格的双弹性，借助数理方法，从厂商、政府和均衡的角度，从内、外部需求失衡两个方面进行研究；分析劳动力的流出，流出者对滞留者的影响，最优货币政策，最优流动等议题。

二、模型构建与分析

（一）内部需求失衡

借鉴 Obstfeld and Rogoff（1995），Farhi and Werning（2012）和 Farhi and Werning（2014）框架，对此模型及假设加以扩展。考虑三因素：劳动力流动、可贸易产品和不可贸易产品。在货币区，有限的地区的数量为i，且i∈I。关于可贸易商品，在Farhi and Werning（2014）的假设中，被认为其可以无弹性地供给；在竞争性贸易中，其价格调整并可达到市场出清。我们认为可贸易商品因区域不同而价格具有可变性。对于非可贸易产品，他们认为，由垄断厂商中的劳动力来提供。这点，我们暂时不改变。下面，将定义相关变量。

1.偏好、技术与市场

代理人（劳动力）：在货币区中，有一个有限数量j类型的代理人的连续体，且 j∈J。 每一个此类型人的数量为 μj，且。j类型代理人居住在i地区，其约束为：

一个j类型代理人居住在i地区，将会通过消费可贸易商品CiT，j和非可贸易商品以及使用劳动力 Ni，j来最大化其效用函数：

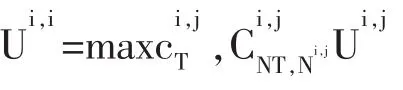
其预算约束：

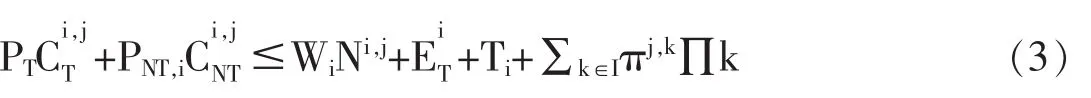
PT为可贸易商品价格；PNT，i为i地区不可贸易商品价格；Wi为i地区工资水平；πj，k为来自于k地区利润∏k的份额，此利润归属j类型代理人并满足∏k=1；Ti是独立于 j类型的 i地区代理人得到的折扣；为 j类型的代理人可贸易商品的禀赋。

当然，代理人只能在其居住地工作和消费；其在可贸易商品上的禀赋是不可剥夺的且不依赖于其所居住的地区；代理人可拥有所有地区的厂商的股份。所有税收与转移具有地区特质性，并不依赖于其所属代理人类型；在货币区的任何一个小区域内，不存在基于过去居住地的、对代理人的歧视。代理人的一阶条件：

若代理人可自由选择居住地区， 其附加条件是：

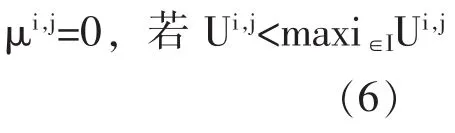
代理人流动的偏好与成本都隐含在效用函数方程Ui，j中。

在我国，当前劳动力无法有效地自由流动并选择其愿意居住的地区，还存在着对农村户籍的歧视，这很难在短期内得以消除。真实情况可能是：μi，j≠0，即使

若可贸易商品能够在竞争下进行交易，此商品的平均禀赋可定义为：Et=

也存在着一些商品，如烟草，实行专卖制度。在一国范围内，其在不同地区出售，将会有不同的价格，此价格会受到相关部门的管控。所以，所谓的可贸易商品的可竞争性交易就可能不存在。关于Et的定义，也没有任何意义。所以，这种情况也得考虑。

厂商：在每一个地区i，由竞争性厂商生产的不可贸易商品联合组成了一个关于不可贸易商品的连续体。此不可贸易商品种类可标记为l，且l∈［0，1］。利用CES生产函数法，算出关于规模CES条件下的恒定收益：，ε＞1。

垄断厂商根据线性技术所生产的不可贸易商品可被定义为：YNT，i，l=AiNi，l

假定每一个垄断厂商在竞争性市场中雇佣劳动力所支付的工资是Wi；向劳动力 τL，i支付地区特质的税收净额为 Wi（1+τL，i）；只有中间产品与最终产品，中间产品的价格是既定的且固定的，也是对称的，即 PNT，i，l=PNT，i。

具有两个式子 YNT，i，l=YNT，i和 Ni，l=Ni的对称均衡必满足：

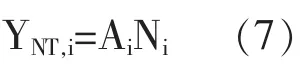
来自于 i地区的中间产品总利润可定义为：∏i=（1-τπ，i）

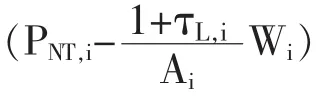
τπ，i为利润税；中间厂商雇佣劳动力以达到需求的固定价格为 PNT，i。

厂商这样做的前提是厂商的努力没有必要。 故，1-τπ，i＞0。 若政策放宽且政府鼓励某些产业优先发展，τπ，i=0 的情况也可考虑。

政府：在每一地区的政府预算约束为：

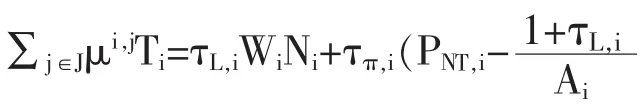
假定：有一个单一的货币区范围内的预算约束（等于所有货币区内小地区的预算约束的总和），可以使得劳动力在货币区内流动。

对均衡的定义：PNT，i为既定价格；为禀赋；πj，i为利润份额；τL，i和 τπ，i为税收；由一群人μi，j形成的不自由流动的均衡必然满足（1）式；可贸易商品的价格为PT；工资为Wi；消费与劳动力供给分别是产出水平为 YNT，i；劳动力需求为Ni；利润为∏i；税收为Ti。消费者最大化；厂商达到需求，该雇佣劳动力，支付税收并分配利润；政府拥有预算约束并使得市场出清。基于（3）式中预算约束，（4）和（5）式的一阶条件以及方程（7）、（8）、（9）的市场出清条件是：

在最理想情况下，即 μi，j≠0，若假设每一个代理人都是理性的人，即以个人利益最大化为目的。 一旦 μi，j≠0，即使则劳动力不能自由流动的状态将不会保持很久，则（6）式就不可能成立，此处条件将难求解。

2．对偏好、税收与禀赋的附加假设

以可贸易商品为例。若利润被全部课税，即 τπ，i=1，从（8）式知，有∏i=0。税收平等地分配到每一个居民，即：

μi为居住在地区的人数，其满足：

这里考虑的是对利润全部征税。由于最优货币区内有特殊政策，所有可贸易商品未必全部征税或者部分商品也可免税，即 τπ，i＜1 或 τπ，i=0，将会有∏i＞0。可见，对全部可贸易商品的利润都征税的做法，也不是明智之举。

（13）和（14）两式隐含的假设是：可贸易商品的禀赋独立于代理人j，即=ET；居住在地区的所有代理人有相同的非劳动性收入PTET+Ti。

若在任意一个i地区，效用函数Ui，j代表所有代理人的相同偏好序数；偏好在消费和劳动力之间可分离，但在消费上是相同的。 即：

这是一个次效用函数。假设是个一次齐次性的，递增的，凹的，严格准凹的，且三阶连续可微；i地区的可贸易商品的相对价格是；在i地区的j类代理人所选择消费的可贸易和不可贸易商品的固定比是：

函数αi（·）是递增且可微的，因为不可贸易商品的价格黏性和缺乏货币政策独立性，限制了地区相对价格Pi的可能变化。

i地区所有代理人j都选择相同的工作量，即总收入（包括劳动和非劳动收入）为其独立于代理人的类型 j。 对于居住在 i地区的所有代理人，关于消费和劳动力的分配是独立于其类型j。

现实并非如此。居住在i地区的所有不同类型的代理人，其在学历、经历、能力方面，未必相同；地区不同，政策不同，流动性也不一样。从而，其总收入必然是不尽相同的。 这说明，均衡状态不是唯一的，或根本不存在。

（二）内部需求失衡下的均衡与最优化

1.均衡

可实现性条件。根据前面的附加定义，i地区的代理人j对可贸易商品和不可贸易商品的消费和对劳动的提供可定义为：

地区的总产出和劳动力可定义为：

可从前面的式子中求出工资Wi和税收Ti。

结论1：（可实现性）可贸易商品的价格既定为PT，当劳动力自由流动时才存在唯一均衡，若劳动力不自由流动时，均衡将会不存在或不唯一；当人口规模为 μi，且 μi，j满足公式（14）时，劳动力不自由流动下的均衡才是唯一的；若公式（14）不能成立，则劳动力不自由流动下的均衡将会不存在或不唯一。

地区水平下的需求失衡的有效衡量工具应是劳动力工资，即

若公式右边的部分独立于代理人的类型j。当τi＞0时，当地经济萧条；当τi＜0 时，当地经济繁荣。

我们认为，的值也需要讨论。若其大于1，则所考察的地区的经济是不断繁荣的，是向上的。若的取值范围在大于0且小于1时，所考察的地区的经济是向上的，但是极其缓慢的。我们认为，应该更关心第二种取值范围。

流动对滞留者的影响。

结论2：（人均安置对居住决定的独立性）当所有代理人j偏好是一致的且可贸易商品的价格既定为PT时，在地区的所有代理人j的安置都是相同的，并由方程（15）—（17）中自由流动或不自由流动下的所有均衡来决定。但若这种偏好具有非一致性时，在i地区的所有代理人j的分配都未必相同。

假定可贸易商品的价格既定为PT，地区i所有代理人j的安置都是完全独立的。当然，当一些代理人流出地区i，减少了当地人口μi，在地区不可贸易商品的总需求也必然下降，这也减少了地区i的劳动力需求。此流出，也会减少地区i的劳动力供给。这种对于滞留者的净影响也可能是零，因为其安置保持不变。当然，流出者得到了一个不同的安置。流出者对滞留者没有影响，比如说，工资水平τi，可能没有受到影响。

但是，如果地区i的经济在不断发展中或者当地的人口生育或增长有限，这种流出可能只会减少劳动力的供给，但不会减少劳动力的需求。从而，当地的劳动力就非常缺乏，流出者对滞留者是有影响的，而且这种影响可能还很大。比如，工资水平τi，可能会有很大程度上升。所以，经济发展水平和人口问题，也应该考虑在内。

2.社会最优化

考虑一个能够描述受约束的帕累托最优的策划问题。这个问题，将被一组非负的帕累托权重 λi来定义，定义间接效用函数：

若可贸易商品的价格PT能够为货币政策所控制。由于研究劳动力流动时没有考虑到所选择的货币政策是否为最优的，这里考虑两个问题：受约束力的策划问题和完全的策划问题。在研究前一个问题时，假定货币政策是既定的，即可贸易商品的价格PT是既定的，最优化地安置地区内的代理人。即：

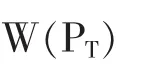
其约束条件是：

而完全的策划问题，允许货币政策具有弹性，并同时描述地区内代理人的最优安置和最优的货币政策。在（18）式中，价格PT是一个选择变量而非一个参数，最大化问题应该关于PT和μi，j。求解关于（18）式的既定价格PT下的有关代理人的最优安置，PT是最大化处理，得：

3．既定货币政策下的最优流动

考虑式子（18）的解。 关于 μi，j的一阶条件为：

Vj即为式子（19）的乘数。 当 μi，j∈（0，1）时，ρi，j=0；当 μi，j=1 时，ρi，j≥0；当μi，j=0 时，ρi，j≤0。 若用 Ui，j来替代 Vi，j，对于一切的 i∈I，j∈J，式子（21）的一阶条件为：

μi，j=0，若

这与自由流动下（6）式的结果类似。如果现实情况如此，对流动的干预也没有太大必要了。 在现实中，若则未必就有 μi，j=0 恒成立了。此情况，也得考虑进去。

结论3：（最优流动）既定货币政策（PT是既定的）下的受约束的有效安置与自由流动时是一致的，干预是没有必要的。 但若有效安置与自由流动时是不一致的，最优的流动就难以保证了，干预是有必要的。

这表明，若没有外部的代理人有关安置决定的对其他代理人的影响，自由流动可能是最优的。但现实中，一个地区的代理人的有关安置于何处的决定而不会对其它代理人的安置决定有任何影响，是很难办到的。这要求我们进一步假设：不同居住地内居民的任何偏好都是完全不同的且相互独立的，一个代理人的决定才不会对其它代理人的决定产生任何影响。所以，只有当情况如此时，就能很容易地达到了。

4．最优货币政策

这里研究（20）式的解。关于不可贸易商品的相对价格的间接效用函数的导数为关于 PT的一阶条件为

结论4：（最优货币政策）当价格ΡΤ是既定时，受约束的有效安置就是地区 ι的劳动力工资 τi的加权平均数等于零， 且关于 τi的权数由来决定；但若PT不是既定的，而是一个随机变量时，最优的货币政策将难以存在。

若PNT，i既定，此分析与具有粘性价格与弹性工资的模型完全相同。由上述式子可知，若价格与工资同时具有弹性时，这种结论难以成立。从而式子（23）也就难以保证了。

结论5：考虑到具有设定为Wi黏性工资的模型、相关均衡及最优安置，其结论都与由式子（23）来决定的黏性价格模型的结论相同；但当价格与工资同时具有弹性时，这种结论便不一定成立。当价格不具有弹性及工资Wi不是既定时，这种结论也不会成立。

这说明，黏性工资的假设至关重要。一旦工资与物价同时所具有的弹性是一样的时候，这种结论将难以存在。所以，工资与物价的此种情况也应该考虑在内。在最优货币区内，未必就是价格具有弹性且工资具有黏性，或者价格具有黏性且工资具有弹性。也有可能，二者的可调整程度是一样的。

（三）外部需求失衡

假设，有一个有限的地区i（i∈I）形成一个货币区；每个地区生产单一的有差异的最终产品；商品都由地区来标识；生产是独特的，但消费不是；冲击造成生产率和偏好变化；由于名义刚性且所有地区都处于货币区之内，价格（工资）不会随着冲击而变化，只会使安置偏离于弹性价格结果；价格（工资）是既定的，只考虑一次非预期冲击。

1．偏好、技术和市场

代理人 （劳动力本身或居民）：有一个有限数量的类型代理人的连续体，j∈J，每一个此类型的人的数量为 μj且 μi，j∈［0，μj］。 j类型的代理人居住在地区，约束为：

一个j类型的代理人居住在地区，通过一个具有劳动力Ni，j和最终产品的消费函数

从（22）的结果可知，最优货币政策或受约束的有效安置能够产生，将主要受制于价格变量的形态和劳动力工资的情况。若价格是随机变量或劳动力工资的加权平均数不等于零，此种最优货币政策或有效安置将无法产生。只要价格和工资都具有弹性或者其黏性和刚性很小，最优的安排就难以实现。可见，弹性在一定程度上也对结果有重要的影响。

5．粘性

前面论证的结果都依赖名义刚性。现在，依然考虑相同的模型，但价格是弹性的，工资Wi是黏性的。假设工资是既定的。考虑一个简单的均匀安置规则，即在地区i的劳动力Ni在居住在地区i的代理人中平等地分配。最优价格设置表明：来最大化其效用。 即

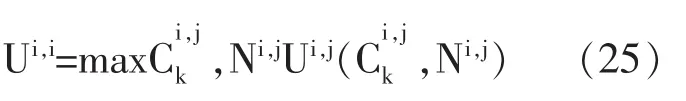
其预算约束为：

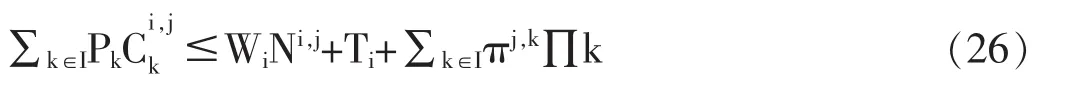
Pk为最终商品k的价格；Wi为i地区的工资水平；πj，k为j类型代理人的来自于k地区的利润∏k的份额；Ti是独立与类型的i地区的代理人所得到的总的转移支付。

对于所有的i，代理人的一阶条件是：

若代理人能够自由地选择居住地，则附加条件是：

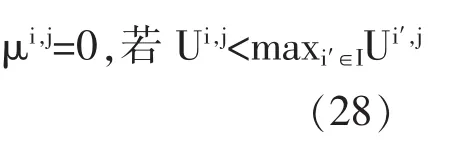
代理人流动的成本都隐含在效用函数方程Ui，j之中。

当前，劳动力无法自由流动并选择其所愿意居住的地区。目前，仍然存在着对乡村户籍的歧视，也很难在短期内得以消除。这表明，城乡二元制户籍仍然是有区别的，一线城市及其与二、三线城市在对待劳动力流入上有诸多限制条件。这样，我国目前的劳动力自由流动的假设难以在现实中发生。真实的情况可能就是：μi，j≠0，即使

厂商：在每一个地区i，由竞争性厂商生产最终产品。这些厂商联合组成了一个关于不可贸易商品的连续体。此商品的种类可标记为l，且l∈［0，1］。利用CES生产函数方法，可算出关于规模CES条件下的收益：Yi=，ε＞1。

垄断厂商根据线性技术所生产的每一种类不可贸易商品可定义为：Yi，l=AiNi，l。

若定每个垄断厂商在竞争性市场中雇佣劳动力所支付的工资是Wi，向劳动力 τL，i支付地区特质的税收净额为 Wi（1+τL，i）；价格 Pi，l=Pi由垄断厂商决定，具有黏性，是既定的；所有中间商在既定地区都雇佣相同数量的劳动力Ni。即：

中间产品的一般价格Pi，也即是在地区所生产的最终产品的价格。

来自于 i地区的中间产品总利润可定义为：

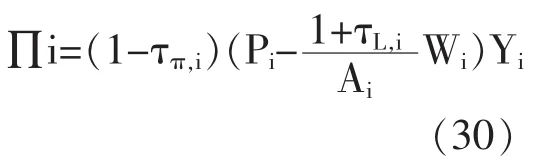
τπ，i为利润税，利润份额需满足：

厂商这样做的前提是，≤0，厂商的一切努力没有必要。关于中间产品的一般价格Pi的假设，蕴涵两点说明：其一，一切与商品有关的交易成本可能等于零，如加工费用、运输费等等。其二，商品能够在货币区内自由流动。但是，交易成本等于零的说法难以成立。一方面，中间产品不等于最终产品，中间产品一般都需要经过某种程度地加工才能变成最终产品，这也就决定了相关费用或成本的存在；另一方面，加工费和运输费等都等于零，完全不符合当前物流业或服务业高度发达的社会现实。从当前我国的现实来看，并非所有商品都是自由流通的，某些商品在地区间的限制还是存在的。 原则上，1-＞0；若政策放宽且政府鼓励某些产业优先发展，τπ，i=0 也可考虑。

政府：每一个地区的政府预算约束：

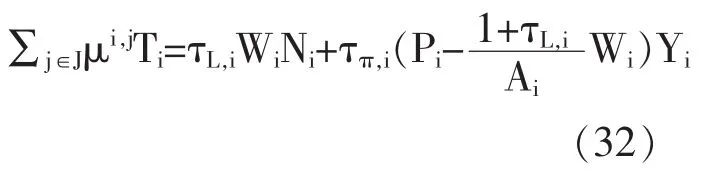
对均衡的定义：若 Pi为既定的价格；πj，i为利润份额；和为税收；不自由流动的均衡是以下变量的集合：即一群人工资为Wi；消费与劳动力供给 分别是，Ni，j；产出水平为 Yi；劳动力需求为 Ni；利润为∏i；税收为另一方面，消费者最大化；厂商达到需求，该雇佣劳动力，支付税收并分配利润；政府拥有预算约束并使得市场出清。基于（24）—（27）式及（29）和（32）式的一阶条件，市场出清条件成立，则对于k∈I：

在最理想时，即 μi，j≠0，若假设每一个代理人都是理性的人；一旦≠0，即使劳动力不能自由流动的状态将不会保持很久，则（33）式也不可能成立。从而，此处的条件可能就难求了。

2．对偏好与税收的附加假设

假设利润被全部课税，即 τπ，i=1，从（30）式可知，有∏i=0。 而且，税收平等地分配到每一个居民，即：

μi为居住在地区的人数，其满足：

这里考虑的只是对利润全部征税的做法。若由于最优货币区内有特殊政策，即所有可贸易商品未必全部征税或者部分商品也可以免税，即τπ，i＜1或τπ，i=0，将有∏i＞0。所以，对全部可贸易商品的利润征税的做法，也未必就是一个明智之举。因为，虽然政府可以从中得到收益，但厂商可能不愿意从事生产活动。这样，生活在货币区内的代理人的福利也可能会受到影响。

若所有居住在地区的所有代理人有相同的收入，并由在地区生产的最终产品的价值来确定；每一个地区都有一个平衡预算：

当然，在任意一个地区，其效用函数Ui，j都代表了所有j类代理人的相同偏好序数；偏好在消费和劳动力之间是可以分离的，但在消费上是相同的；∈（0，1）为在商品 k 上的支出份额，且；偏好的选择具有足够的弹性，能够允许任意程度的关于消费的本土偏好；Pi为相关价格指数，Ci，j为消费指数。 一个居住在 i地区的 j类型的代理人的效用可以定义为：这里，有三点值得讨论：

首先，基于（35）和（36）两式及后方的假设，其隐含之意是：每一个居民的产生都是相同的。只有这个假设成立，才能说明税收都平均地分配到每一个居民身上。但实际生产活动中，由于每个居民的要素禀赋不同，所分配的也未必全都相同，且每个居民的技术程度和劳动效率也不尽相同。从而，税收不应该平均分摊，而应该考虑差异化。

其次，所有代理人都有相同的收入且由其生产的最终产品的价值都由来确定，这一做法也值得商榷。前面已说明过，因为要素禀赋和技术水平的差异，居民的收入水平应该是不同的。此外，居民收入除了与生产的产品数量有关以外，还与商品的需求、生产成本、物流费用、政府税收等多方面因素相关，未必只唯一地由其生产的最终产品的价值来确定，即由来确定。

再次，偏好在消费和劳动力之间未必是可分离的。前面已假设居民为理性的经济人，则其必以个人利益最大化为目标。若劳动力各方面条件都很优秀，其本身能够得到更多收入，可得到更多更好的消费品；相反，若一个劳动力各方面都比较欠缺，则其本身将难以得到相当多的收入，从而其进一步消费的欲望可能会受到限制。所以，偏好与劳动力本身还是存在着一定的相关性，即偏好与劳动力本身也可能难以分离。

（四）外部需求失衡下的均衡与最优化

1.均衡

可实现性条件：根据上文的假设条件，i地区的总收入由PiYi来定，则地区对商品k的总需求为。将所有货币区的需求加总，得到总需求。k地的收入为：

可见，一个地区的总收入全部固定在产品价格和产出水平上，即与劳动相关。但现实情况是，居民除了拥有劳动性收入，也可能有非劳动性收入。如，专利权、租赁权等等。所以，居民的全部收入应大于既定收入水平PkYk。进一步假设，商品在货币区内是可以自由流动的且价格是一定的。

结论6：（可实现性）：在一个劳动力自由流动和不自由流动的均衡中且不存在其它非劳动性收入时，区域产品Yi必需满足上述可实现性条件。对于既定的区域产出Yi必需满足上述可实现性条件。当区域性人口规模μi满足（36）式且价格一定时，具有区域产品Yi且劳动力不自由流动下的均衡是唯一的；一旦价格不能确定或是不连续的随机变量时，这种均衡可能不唯一或不存在。

我们认为，一旦商品不能在货币区内自由流通，而且商品价格是不确定的，而是不连续的随机变量。只要存在其它形式的非劳动性收入，（37）式就不成立。即使它成立，（37）也无解或不止一个解，即均衡的唯一性也不存在。

若 Yi＞0且（37）式成立，则由 Yi决定的总产出为：

价格指数为：；地区水平下的需求失衡的有效衡量工具应该就是劳动力工资，即

假定公式右边的部分独立于代理人的类型j。当τi=0时，表明最佳的安置；当τi＞0时，表明当地经济处于萧条；当τi＜0时，表明当地经济处于繁荣。

我们认为的值也得讨论。若其大于1，则表明所考察的地区的经济是不断繁荣的，是向上的。若取值范围在大于0且小于1之间，所考察的地区的经济是向上的，但是极其缓慢的。所以，第二种取值范围可能是我们应该更关心的。

结论7：（需求结构）：在每一个货币区，商品价格都是既定时且非劳动性收入不存在时，存在一个严格递增的区域性产出，对于所有满足（37）的产出 Yi，都存在一个 λ＞0，对于所有的 i，都有=λ成立；若商品价格不能既定时，

从需求结构的角度来看，商品价格能否既定以及非劳动性收入是否存在，仍然是一个严格递增的区域性产出能否存在和Yi=λ能否成立的关键因素。若在货币区内部，某些商品的价格是不确定的，或者是一种不连续的随机变量，此式就不存在。非劳动性收入，也是要考量的一个因素。只要非劳动性收入存在，（37）式就难成立。

结论8：（人均安置对居住决定的依赖性）令λ＞0，在自由流动和不自由流动的均衡中，在i地区的所有代理人j的消费和劳动安置是由（37）和（38）式决定，这种安置取决于i地区的人口规模μi的有效统计而得到的均衡，且λ与μi是呈反比的。在每一个货币区，商品价格都不是既定的且非劳动性收入存在时，（37）和（38）两式将不成立，λ与μi的反比关系也将不会存在。

同理，从需求结构的角度来看，商品价格能否既定以及非劳动性收入是否存在，仍然是λ与μi的反比关系能否成立的关键因素。

2．社会最优化

考虑一个计划问题，其标记为一个非负的帕累托权数λj。通过改变此权数可以算出整个受约束下的帕累托边界，计划者在无自由流动下的一系列均衡中最大化。所考虑的两问题是：一个受约束下的计划问题，一个完全的计划问题。在讨论第一个问题时，货币区范围内的总需求管理λ是既定的，我们主要是去寻求在货币区内最优地安置代理人。利用结论7和结论8，此问题可写作：

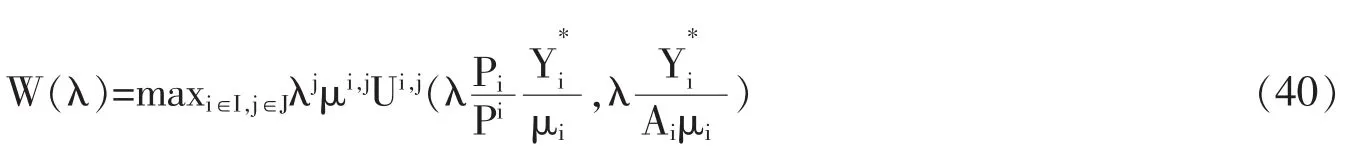
对于所有的 j∈J 和 i∈I，都有两式成立。

此问题要求弹性的货币政策，同时以地区间代理人的最优安置和最优货币政策为特征。第一个计划问题中（40）式的唯一差别就是：λ是一个选择变量而非一个参数。这样，最优化问题就与λ、μi和μi，j相关了。此计划问题可以通过递归方式来解决，这也解决了有关限定的、以受约束计划问题为特征的λ和有关λ最大化的地区间代理人的最优安置问题。

若λ是一个参数而非一个选择变量，最优化问题就与μi和μi，j相关，（41）式可改写成：

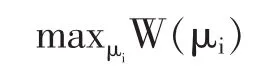
3．最优流动

我们主要描述既定货币区范围内总需求管理（受约束计划问题（40）式之解）下的受约束的有效安置问题。此处，受约束的计划问题可被分为两个步骤。第一步，解下式：

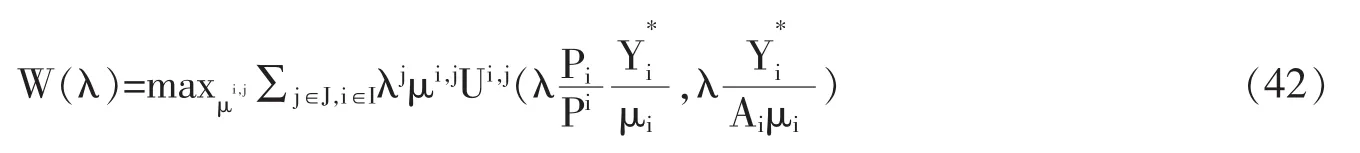
其约束条件为：

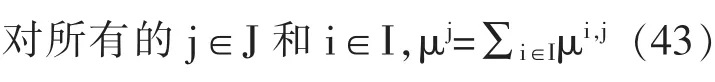
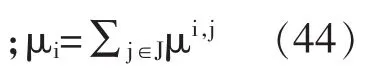
第二步，解式子：其约束条件为：

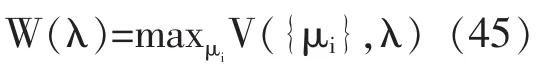
对所有的 j∈J和 i∈I，可得到在第一步的计划问题（42）式中关于 μi，j的一阶条件：

γi为约束（44）式的乘数；vj为约束（43）式的乘数；当 ρi，j∈（0，1）时，ρi，j=0；当 ρi，j=1 时，ρi，j≥0；当 ρi，j=0 时，ρi，j≤0。

根据包络定理，对于所有的 i∈I，有：

这要求等式右边的项目要独立于代理人的类型j，否则，上式将无法成立。对于所有的 i∈I，计划问题（45）的一阶条件为：Vμi=γ，即：

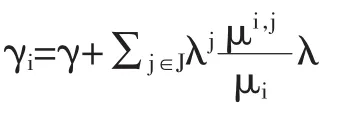
γi-γ 与劳动力工资 τi相一致。 若地区 i是繁荣的，则 τi＜0 且 γi＜γ；若地区i是萧条的，则 τi＞0 且 γi＞γ。 一阶条件（46）式也可变换为：对所有的 j∈J和 i∈I，有：

与（28）式比较后可知，与最大化目标Ui，j是不一样的。所以，劳动力的流动应该被干预。其干预的方式之一，便是通过一个在地区i和地区i′之间的效用对比情况下的暗示性的且附加的效用工资来实现。此效用工资既定为

显然， 因子和因子的大小关系是决定干预劳动力流动与否的关键因素。若，则 μi，j≠0，这种干预也没有必要和意义。

结论 9：（最优流动）若恒成立，既定货币区范围内总需求管理条件下的受约束的有效安置，通常与自由流动不一致；此时，劳动力的流动应该利用效用工资的方式来干预，地区i和地区i′之间的效用对比情况下的效用工资既定为，且λi由方程（47）来定义。 但若≥，则≠0，既定货币区范围内总需求管理条件下的受约束的有效安置，通常与自由流动可能就是一致。这时，劳动力的流动应该不需要干预，也不需要利用效用工资的方式来干预。

此结论说明，若恒成立，在一个自由流动的均衡中，代理人趋向于不愿意居住在一个相对繁荣但具有低值γi的地区，而趋向于居住在一个相对萧条但具有高值γi的地区。或者说，代理人不愿意从一个相对萧条的地区移入到一个相对繁荣的地区。

一旦，在一个自由流动的均衡中，代理人就很愿意从一个相对萧条的地区移入到一个相对繁荣的地区。

此结论也说明，代理人可能没有认识到，通过从萧条地区移出，他们能相应地增加滞留在那一地区的代理人的消费和劳动力供给。因为，全体总消费和劳动力供给在地区i都保持不变，并由于向外迁移而在较少的人口之间分享。

这种推理的前提是：滞留在萧条地区的居民的边际消费倾向保持递增且当地的就业情况在不断地改善（或经济在不断地增长）。否则，滞留在那一地区的代理人的消费和劳动力供给将难以增加，这样一来，后方的诸多结论将也不会成立了。

只有当这种隐含的前提成立时，滞留的代理人的效用影响力与那一地区的劳动力工资τi才是相对称的。假设一群代理人离开了地区i，且-dμi＞0。这样，类型的滞留者的效用函数的变化可写作：

当这种隐含的前提成立时，通过对比结论3和结论9可知，受约束的有效安置与自由流动是一致的，且代理人的流动决定对其它代理人没有外部效应。但若这种前提不成立时，就很难保证受约束的有效安置与自由流动是一致的，以及代理人的流动决定对其它代理人没有外部效应。这里也还需要假设：生活在地区的类型的代理人的安置独立于货币区内代理人的分配情况。相比之下，在外部失衡的模型中，受约束的有效安置一般与自由流动是否一致，代理人的流动决定是否对其它代理人的效用有外部影响，这都将取决于上述隐含的前提假设是否成立。即，若隐含的前提假设成立，则在外部失衡的模型中，受约束的有效安置一般与自由流动是一致的，且代理人的流动决定对其它代理人的效用有外部影响。否则，这种说法将不成立。

我们认为，在内部失衡的模型中，对于既定立场下的货币政策ΡΤ，从某地移出的做法将会减少该地区非贸易商品的总需求。以及在减少该地区相同数量的劳动力的总需求，因为该地区劳动力的总供给得到了减少。最终，滞留者的劳动力供给没有变化，其消费也是如此。若以上隐含假设不成立，此种推理也是错误的。

假设滞留者所处的地区的经济在不断增长，劳动力需求不断增加，消费不断上升。相比之下，对于货币区范围内总需求管理λ的一个既定的立场，在外部失衡的模型中，代理人从一个地区移出并不减少此地区产品的总需求。因为，这种产品的总需求可以通过滞留者劳动力的增加而得到，这也增加了其收入和消费。所以，若此前提假设不成立，即滞留者所处地区的经济不能增长，或劳动力需求不能增加，滞留者所处地区的劳动力需求将会进一步减少。这样，就更别提收入和消费的增加了。

4．最优的货币区范围内总需求管理

研究受约束的有效安置，即（41）式的解。 其一阶条件

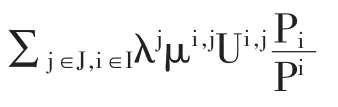
假设，等式右边独立于所有的j∈J。

结论10：（最优的货币区范围内总需求）当λ是一个选择变量而非一个参数时，受约束的有效安置是：地区i范围内劳动力工资τi的加权平均数，它等于零，这种结果主要由因子来决定。

若一阶条件（49）式成立，必有0成立。由于劳动力工资 τi＞0，μ＞0，P＞0，Y＞0，则必有≤0的情况存在。所以，λ不仅影响内生变量Ui，j，也影响结论9中的最优流动条件。因为，在此条件中，其余的变量从经济学的意义上来看，一般不会等于零。所以，因子对于（49）式能否成立有重要的决定性。

假设的条件之一便是：λ是一个选择变量而非一个参数。若λ不是一个选择变量而是一个参数（λ≠0），因子对于（49）式能否成立有更加重要的决定性。

5．粘性

上文都假设价格是弹性的，工资是黏性的，工资Wi是既定的。我们再次考虑一个类似的、简单的均匀安置规则，即在地区i的劳动力Ni在居住在地区的代理人中平等地分配。其最优价格设置表明：

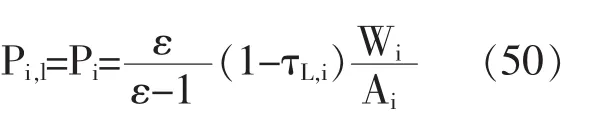
若价格设置Pi既定，此分析与具有粘性价格与弹性工资的模型完全相同。但由上式可知，一旦价格与工资同时具有弹性时，这种结论便难以成立了，即（50）式也未必能成立。

结论11：考虑到具有黏性工资的模型和相关均衡及最优安置，其结论都与由式子（50）来决定的黏性价格模型的结论相同；但当价格与工资同时具有弹性时，这种结论未必成立。当价格不具有弹性及工资Wi不是既定时，这种结论也不会成立。

一旦工资与物价所具有的弹性是一样的时候，这种结论将难以存在。所以，工资与物价的此种情况也应该考虑在内。在最优货币区内，未必就是价格具有弹性且工资具有黏性，或者价格具有黏性且工资具有弹性。也有可能，二者的可调整程度是一样的。

三、可行性建议

基于以上主要结论和福建省劳动力流动的现实，为了防范自贸区金融风险，我们建议：

当货币区的失衡主要来自于内部时：

（1）若一个货币区的经济在不断发展中或者当地的人口生育或增长有限，则劳动力流出可能只会减少劳动力的供给，但并没有减少劳动力的需求。所以，当地的劳动力就非常缺乏，流出者对滞留者是有影响的。此时，政府可以适当鼓励人口增加的政策或适量引入外来人口，以满足本地区的就业和经济增长之需要。当然，提升货币区内的工资水平和福利水平，也是吸引劳动力流入的较好方法。

（2）引导价格在一个较为合理的范围内波动，避免价格的大涨大跌，可促成最优货币政策或有效安置的产生。

当货币区的失衡主要来自于外部时：

（1）为达到最优的需求结构，可考虑适当地管理劳动力的非劳动性收入。

（2）为合理引导劳动力流动，若既定货币区范围内总需求管理条件下的受约束的有效安置与自由流动一致时，劳动力的流动应该不需要干预，也不需要利用效用工资来干预。

［1］Bonin， Holger， Werner Eichhorst， Christer Florman， Mette Okkels Hansen， Lena Skiold，Jan Stuhler， Konstantinos Tatsiramos， Henrik Thomasen， Klaus F．Zimmermann．Geographic Mobility in the European Union： Optimising its Economic and Social Benefits［R］．IZA Research Reports，NO．19， Institute for the Study of Labor （IZA）， July 2008．

［2］Dellas， Harris， George S．Tavlas．An Optimum-currency-area Odyssey［J］．Journal of International Money and Finance， 2009，28（7），1117-1137．

［3］Farhi， Emmanuel， Ivan Werning．Fiscal Unions［R］．NBER Working Papers 18280， National Bureau of Economic Research，Inc June 2012，revised March 2017 ．

［4］Farhi， Emmanuel， Ivan Werning．Labor Mobility within Currency Unions［R］．NBER Working Paper No．20105，National Bureau of Economic Research， May 2014．

［5］Friedman， Milton．The Case for Flexible Exchange Rates［M］//Milton Friedman．Essays in Positive Economics［M］．University of Chicago Press， 1954：157-203．

［6］McKinnon， Ronald．Optimum Currency Areas［J］．American Economic Review， 1963（53）：717-724．

［7］Meade， J．E．The Balance of Payment Problems of a Free Trade Area［J］．Economic Journal，1957（67）：379-396．

［8］Mundell， Robert．A Theory of Optimum Currency Areas［J］．American Economic Review，1961，51（4）：657-665．

［9］Obstfeld， Maurice， Kenneth Rogoff．Exchange Rate Dynamics Redux［J］．Journal of Political Economy， 1995，103（3）：624-60．

［10］Scitovsky， Tibor．Economic Theory and Western Economic Integration［R］．Stanford， 1958．