基于反应扩散和非局部自相似的图像去噪算法
2018-06-28莫佩基
莫佩基,雷 宏
(1.中国科学院电子学研究所,北京 100190; 2.中国科学院大学,北京 100049)
0 引 言
图像去噪作为低层次视觉中的经典问题,是图像处理的基础与难点,从20世纪70年代发展至今仍是一个研究热点。一般而言,图像去噪主要是从含噪图像y=x+v中恢复原始干净图像x(v假定为加性高斯白噪声)。去噪方法种类繁多,主要有滤波[1]、扩散[2-3]、全变分[4-5]、小波或曲线波[6-8]、稀疏表示[9-12]、非局部自相似性(Nonlocal Self-Similarity, NSS)[13-17]、NSS与扩散结合[18-19]等。
尽管在图像去噪中NSS早已证实了它的有效性,但现存的绝大部分算法,只是利用了输入噪声图像的NSS,而没有考虑干净图像的NSS。因此,Xu等[20]提出了PGPD算法,其利用干净图像学习得到块组(Patch Group, PG)的非局部相似性先验,然后利用基于PG的高斯混合模型(Gaussian Mixture Model, GMM)算法[21]和加权稀疏编码对图像进行去噪。该方法去噪效果和运行效率都非常好,但随着噪声水平的增加,去噪性能会下降,不能很好地保持图像边缘、纹理等细节信息。
对图像的小波分解而言,低频部分主要为图像有用信息,而高频部分包含图像的边缘、纹理以及噪声,并且,图像信号的小波系数要高于噪声的小波系数[16]。
基于以上分析,本文提出一种反应扩散与PGPD相结合的图像去噪算法,主要思想是对PGPD去噪图像进行小波分解,按照高低频及阈值划分为3个正交子带。经过理论分析与实验仿真,可知高频系数值大的部分多为图像边缘和纹理,去噪时对该部分锐化能力较差,因此最终的峰值信噪比(Peak Signal to Noise Ratio, PSNR)偏低,而反应扩散模型[22]恰好可以保护边缘,因而可以利用其对该部分进行锐化。实验结果表明,所提算法较之PGPD,不仅PSNR值更高,还可以有效保存图像细节和边缘。
1 算法介绍
1.1 PGPD算法
自然图像中会存在信息冗余性,即像素或图像块之间存在颜色和结构上的相似性。也就是说,给定一个图像块,在整个图像范围内通常可以找到许多相似结构的图像块,这就是图像的非局部自相似性(NSS)。NSS的引入大大改善了图像去噪效果,也为去噪领域开创了一条新颖的研究思路。文献[13]提出的非局部均值算法,就是利用图像中的相似像素估计目标像素;文献[14]将相似图像块分组,以组为单位进行维纳滤波以此改善去噪效果;也可结合文献[15]低秩逼近方法进行去噪。但是,上述算法只是利用了噪声图像的非局部相似性特征,没能充分利用干净图像的非局部相似性先验。因此,Xu等人[20]在此基础上提出了利用含噪图像与干净图像非局部相似性的PGPD去噪算法。

假设所有PG独立采样,对总的目标似然函数取最大化,即最大化
(1)
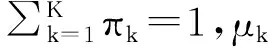

(2)
式(2)的解从最大后验概率估计的角度来看等价于
(3)

虽然经过学习和去噪2个阶段,PGPD算法能够充分利用干净图像和噪声图像的非局部相似性特征,达到较好的去噪效果,但整体对图像纹理细节的保护不够。因此对PGPD算法进行改进,将经过PGPD算法处理后的图像进行小波分解,然后按照高低频及阈值分为3个子带,对含大部分图像细节的高频大于阈值部分用反应扩散模型(TNRD)扩散处理即可。
1.2 TNRD算法
在图像复原问题中,各向异性扩散通过扩散系数在图像的边缘和平坦区域产生相应的锐化或平滑作用,因此可以有效保持图像细节特征。文献[2-3]提出的算法都是基于扩散模型的,其中PM方程尤为经典,很多相关的工作也是由此展开。虽然每个非线性扩散过程都可以等价为一个确定性的偏微分方程(Partial Differential Equation, PDE)形式,但是对特定图像处理问题很难设计出合适的PDE,而Chen等[22]提出了一种基于训练的非线性反应扩散模型(TNRD),主要思想是在训练的过程中不断地迭代优化反应扩散模型中的滤波器与影响函数。由于最终得到的惩罚函数(影响函数是惩罚函数的导数)与传统的惩罚函数明显不同,有些具有多个极小值点,更能增强图像结构,有些可以自适应地对图像进行平滑和锐化,因此可以使用该模型来对PGPD处理后的图像进行锐化。
1.3 改进算法
针对PGPD算法中存在图像边缘保护不足的问题,可以利用反应扩散模型对图像边缘、细节部分进行改进。而图像经过小波变换后,设定合适的阈值thr可以有效将图像中属于边缘、细节的部分提取出来,然后对该部分锐化处理。基于以上的分析,本文所提出的改进算法流程如图1所示。
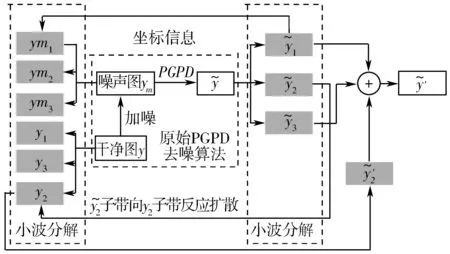
图1 本文改进算法流程图

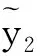
(4)

(5)
(6)
由于图像分解后不同下标(1,2,3)的重构子带彼此正交,因此式(6)最后展开为:
(7)
获得图像与分解子带均方误差的关系后,接着利用灰度图中PSNR与MSE之间的关系:
(8)
由此推导图像与分解子带PSNR的关系,有:
(9)
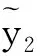
2 实验结果与分析
实验仿真利用Matlab R2015b实现,运行环境为Intel i5双核处理器,8 GB内存。对比算法分别为基于图像非局部自相似性的主流算法:BM3D[14]和PGPD[20]。

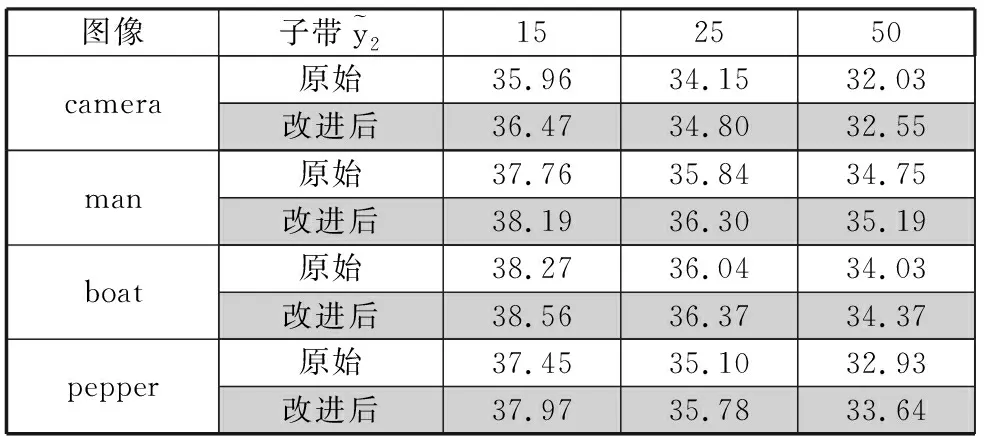
表1 改进前后子带PSNR值 单位:dB
表2 不同算法去噪效果比较PSNR(SSIM)

图像σBM3DPGPD本文算法camera1531.80(0.892)31.79(0.892)32.01(0.896)2529.33(0.843)29.21(0.841)29.47(0.846)5025.83(0.763)26.38(0.775)26.60(0.780)man1531.90(0.863)31.97(0.865)32.09(0.868)2529.58(0.802)29.65(0.802)29.76(0.805)5026.55(0.687)26.85(0.703)26.96(0.706)boat1532.11(0.854)32.05(0.849)32.12(0.850)2529.86(0.801)29.85(0.796)29.93(0.798)5026.54(0.691)26.84(0.701)26.90(0.703)pepper1532.66(0.902)32.66(0.902)32.85(0.904)2530.10(0.864)30.14(0.866)30.39(0.869)5026.43(0.770)26.77(0.794)26.96(0.797)
同时,选取了2幅添加均值为0,方差为50的高斯白噪声图像进行去噪视觉效果比较。如图2所示,本文所提出的改进算法能够更好地保护图像边缘等细节信息,对局部区域(小方框)进行放大观察(大方框),可以看出改进算法不会过多产生虚假信息。使用方法噪声对改进算法能否有效地保护图像边缘信息进行评估,其为含噪图像与去噪图像的差值。如果方法噪声越接近白噪声,所含图像细节越少,则表明算法去噪效果越好,越能有效保护图像边缘、纹理等细节信息。如图3所示,其为图2中的图像所对应的方法噪声,将其放大观察,可以发现改进算法的方法噪声更接近于高斯白噪声,而BM3D和PGBD的方法噪声中存在明显的图像纹理信息。由此可以看出,改进算法在图像细节保护方面的优势。

(a)干净图 (b)BM3D (c)PGPD (d)本文算法图2 不同算法去噪后的图像

(a) BM3D (b) PGPD (c) 改进算法图3 不同去噪算法得到的方法噪声
3 结束语
尽管PGPD同时利用噪声图像和干净图像的非局部相似性,去噪效果相较BM3D更佳,但对图像边缘、纹理等细节信息保护仍有欠缺,因此本文利用小波分解和TNRD模型对其改进。数值实验表明,所提出的算法可以有效去除噪声并且可以更好地保护图像边缘。但文中所涉及的算法都是在噪声水平已知的情况下进行处理,而在实际应用中,待处理图像的噪声水平往往都是未知的。因此,下一步工作将利用噪声估计方法估计待处理图像的噪声水平,并对反应扩散模型进行改进使其能更有效地向图像的ym2子带扩散。
参考文献:
[1] Tomasi C, Manduchi R. Bilateral filtering for gray and color images[C]// IEEE International Conference on Computer Vision (ICCV). 1998:839-846.
[2] Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on PAMI, 1990,12(7):629-639.
[3] You Y L, Kaven M. Fourth-order partial differential equation for noise removal[J]. IEEE Transactions on Image Processing, 2000,9(10):1723-1729.
[4] Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[C]// The 11th International Conference of the Center for Nonlinear Studies on Experimental Mathematics. 1992:259-268.
[5] Osher S, Burger M, Goldfarb D, et al. An iterative regularization method for total variation-based image restoration[J].SIAM Journal on Multiscale Modeling & Simulation, 2005,4(2):460-489.
[6] Donoho D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory, 1995,41(3):613-627.
[7] Chang S G, Yu B, Vetterli M. Adaptive wavelet thresholding for image denoising and compression[J]. IEEE Transactions on Image Processing, 2000,9(9):1532-1546.
[8] Starck J L, Candes E J, Donoho D L. The curvelet transform for image denoising[J]. IEEE Trans. on Image Processing, 2002,11(6):670-684.
[9] Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006,15(12):3736-3745.
[10] Mairal J, Bach F, Ponce J, et al. Non-local sparse models for image restoration[C]// IEEE International Conference on Computer Vision (ICCV). 2010:2272-2279.
[11] Dong Weisheng, Zhang Lei, Shi Guangming, et al. Nonlocally centralized sparse representation for image restoration[J]. IEEE Transactions on Image Processing, 2013,22(4):1620-1630.
[12] Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006,54(11):4311-4322.
[13] Buades A, Coll B, Morel J M. A non-local algorithm for image denoising[C]// IEEE Computer Society Conference on Computer Vision. 2005:60-65.
[14] Dabov K, Foi A, Katkovnik V, et al. Image denoising by sparse 3-D transform-domain collaborative filtering[J]. IEEE Transactions on Image Processing, 2007,16(8): 2080-2095.
[15] Gu Shuhang, Zhang Lei, Zuo Wangmeng, et al. Weighted nuclear norm minimization with application to image denoising[C]// IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 2014:2862-2869.
[16] 冯象初,李晓晖,王卫卫,等. 方向扩散方程修正BM3D图像去噪改进算法[J]. 西安电子科技大学学报(自然科学版), 2017,44(5):102-108.
[17] 刘向乐,冯象初. 小波域三维块匹配图像去噪[J]. 计算机工程与应用, 2010,46(16):185-187.
[18] Yuan Jianjun. Improved anisotropic diffusion equation based on new non-local information scheme for image denoising[J]. Computer Vision IET, 2015,9(6):864-870.
[19] 张兆伦. 基于非局部均值图像去噪算法研究[D]. 南京:南京邮电大学, 2015.
[20] Xu Jun, Zhang Lei, Zuo Wangmeng, et al. Patch group based nonlocal self-similarity prior learning for image denoising[C]// IEEE International Conference on Computer Society. 2015:244-252.
[21] Yu Guoshen, Sapiro G, Mallat S. Solving inverse problems with piecewise linear estimators: From Gaussian mixture models to structure sparsity[J]. IEEE Transactions on Image Processing, 2012,21(5):2481-2499.
[22] Chen Yunjin, Yu Wei, Pock T. On learning optimized reaction diffusion processes for effective image restoration[J]. Computer Vision and Pattern Recognition, 2015,8(1):5261-5269.
[23] Dempster A P. Maximum likelihood from incomplete data via the EM algorithm[J]. Journal of the Royal Statistical Society, 1977,39(1):1-38.
[24] Mahmoudi M, Sapiro G. Fast image and video denoising via nonlocal means of similar neighborhoods[J]. IEEE Signal Processing Letters, 2005,12(12):839-842.
