基于动态调整惯性权重的混合粒子群算法
2018-06-28顾明亮
顾明亮,李 旻
(华南理工大学机械与汽车工程学院,广东 广州 510640)
0 引 言
粒子群算法是由Kennedy和Eberhart[1]共同提出的。然而,基本的粒子群算法无法选择进行全局搜索还是局部搜索。文献[2]在基本粒子群算法的基础上提出了带有惯性权重的改进粒子群算法,由于该算法在迭代的过程中收敛效果较好,通常被默认为标准粒子群算法。文献[3]提出的线性递减动态调整惯性权重粒子群算法能够在迭代的过程中划分粒子进行局部搜索还是全局搜索,取得了较好的效果。然而,当面对复杂的非线性多维函数优化问题时,算法容易陷入局部最优解。因此,为了能够让算法达到最优性能,非线性权值调整策略逐渐替代线性权值调整策略。非线性函数有很多,常用的调整曲线为正切曲线、正弦曲线和对数曲线等[4-6]。权值调整曲线的变化规律一般为:迭代前期,惯性权重w值较大,此时算法全局搜索能力较强;当进入到迭代后期时,w值较小,此时局部搜索能力得到加强。然而,对于一些非线性多峰函数来说,当算法进入到后期时容易陷入局部最优解,造成算法早熟收敛[7-8]。
为了让粒子群算法在迭代的后期可以搜索到全局最优解,刘爱军等人[9]在标准粒子群算法中加入了混沌搜索策略,利用混沌搜索的遍历性来增强算法全局寻优的能力。赵志刚等人[10]根据迭代过程中适应度的大小关系将处于不同组别适应度的粒子赋予不同的惯性权重。文献[11]提出了基于反向学习的粒子群算法增加种群的多样性。
本文首先通过拉丁超立方体抽样产生初始种群,然后引入适应度方差的概念,并将其与惯性权重调整策略相结合。当方差小于设定的临界方差时,对改进的惯性权重调整公式进行随机扰动,并且引入小生境遗传算法淘汰一些相似的个体,增加种群的多样性,增强算法全局寻优能力。最后通过测试函数对本文改进算法进行性能测试,将结果与其他5种算法结果进行对比,验证此算法的有效性。
1 标准粒子群算法
假定种群的空间为N×D维,其中N代表种群数量;D代表粒子维数;D维向量Xi=(xi1,xi2,…,xiD)表示第i个粒子的位置(i=1,2,…,N),其速度可表示为Vi=(vi1,vi2,…,viD);pbest=(pi1,pi2,…,piD)表示个体极值;gbest=(g1,g2,…,gD)表示全局极值。在获得个体极值与全局极值之后,可以根据式(1)和式(2)来更新粒子的速度和位置。
vij(t+1)= wvij(t)+c1r1[pij(t)-xij(t)]+
c2r2[pgi(t)-xij(t)]
(1)
xij(t+1)=xij(t)+vij(t+1)
(2)
其中,c1和c2为学习因子,也称加速常数;r1和r2为[0,1]均匀分布的随机数;w为惯性权重。
2 改进的粒子群算法
2.1 初始种群的改进
算法一般是以随机方式产生初始种群的位置,这种方式比较容易实现,但是可能会导致种群内个体分布不均匀。因此,本文选用拉丁超立方体抽样的方法产生初始种群的位置[12]。拉丁超立方体抽样(Latin Hypercube Sampling,LHS)可以保证全空间填充和抽样点非重叠,从而使得群体分布均匀。
LHS抽样步骤如下:
step1确定抽样规模H。
step2将每维变量xi的定义域区间[xil, xih]划分成H个相等的小区间,这样就共有Hn个小超立方体产生。
step3产生一个H×n的矩阵A,A的每列均是数列{1,2,…,n}的一个随机全排列。
step4A的每行就只有一个小超立方体被选中,在每个小超立方体内产生一个样本,这样就共有H个样本被选出,且选出的样本互不相同。
通过拉丁超立方体抽样产生的粒子可以充满整个区间,产生的初始种群样本能更好地均匀分布在整个空间,能有效避免出现早熟收敛现象。
2.2 自适应惯性权重的改进
由于惯性权重决定算法在迭代过程中全局搜索占主要部分还是局部搜索占主要部分,因此权值的调整是决定算法性能的关键因素[13]。目前大多数采用的是线性递减动态调整权值策略。然而对于一些非线性复杂函数优化问题来说,使用线性递减权值调整公式时,由于粒子的启发性得不到提高,常常会使得种群陷入局部最优解,导致算法性能大大降低。为了让粒子可以搜索到全局最优解,本文利用非线性函数构造惯性权重进化曲线。由于Sigmod函数在前段和后段变化速度较为缓慢,只需将Sigmod函数稍微修改一下就完全符合惯性权重w的变化规律。因此本文选用Sigmod函数作为构造非线性惯性权重调整的基函数。
Sigmod函数:
(3)
Sigmod函数的变化规律如图1所示。

图1 Sigmod函数曲线
从图1可以看出,Sigmod函数曲线在前段和后段曲线斜率较小,变化速度较慢;在中间处,曲线斜率较大,变化速度较快;并且系数a越大,在曲线前段和后段变化越慢,中间变化越快。为了将Sigmod函数更好地运用在惯性权重调整公式中,本文选用参数a=5。为了使Sigmod函数适用于惯性权重的变化规律,将其变形为式(4):
(4)
然而,虽然粒子的惯性权重调整公式的变化规律为非线性变化,但仍然避免不了陷入局部最优解,此时种群中粒子的适应度大小接近,并且会聚集在局部极值点,粒子出现“靠拢”现象。本文以粒子适应度方差[14]评价种群的多样性好坏。当粒子适应度方差小于设定的临界值时,种群的多样性很差,粒子有可能陷入局部最优解。为了让粒子跳出局部最优解,增强种群的多样性,此时应增大粒子的惯性权重,给予惯性权重随机扰动。
(5)
式(5)中,f为归一化因子,favg为种群平均适应度;σ2为适应度方差;归一化因子f取值如公式(6)所示:
(6)
因此整个惯性权重的调整公式如公式(7)所示:
(7)
式(7)中,ε为设定的适应度方差临界值;rand为[0,1]上均匀分布的随机数。
由于粒子的“靠拢”现象,虽然给惯性权重赋予了较大的数值,仍然有可能陷入局部最优。对于非线性多峰函数来说,当群体多样性较差时,将小生境遗传算法嵌入到粒子群算法中,增强算法的全局寻优能力。
2.3 小生境淘汰策略
小生境技术就是将父代种群与经过交叉、变异操作过后的子代种群合并在一起,通过某种策略(预选择、排挤、分享)选择适应度较好的个体进行下次迭代。小生境策略在小生境距离之内只保留一个适应度较好的个体,大大增加了种群的多样性,是一种较好的全局寻优算法。
小生境淘汰策略算法步骤如下:
step1初始化种群。
step2执行遗传操作(选择、交叉、变异)。
step3将经过遗传操作产生的M个子代个体与N个父代个体合并在一起,得到一个含有M+N个个体的新种群。按照公式(8)计算新种群中每2个个体海明距离。
(8)
当‖Xi-Xj‖ Fmin(Xi,Xj)=Peanlty (9) step4对新种群中个体的适应度进行排序,选择适应度最好的N个个体作为下次迭代的父代种群。 step5若满足算法终止条件则算法停止;否则返回step2。 在对一些复杂的非线性多峰值函数进行优化求解的时候,由于一般的粒子群算法在进化过程中容易过早收敛,陷入局部最优解。本文改进算法是在粒子群算法中嵌入小生境遗传算法[15-17]。算法实现步骤如下: step1初始化粒子群。由拉丁超立方体抽样产生初始种群的位置,初始种群中粒子的速度随机产生。 step2计算粒子的适应度值,确定粒子的个体极值,记为pbest(i);确定粒子的全局极值,记为gbest。 step3根据公式(5)和公式(6)计算粒子的适应度方差;根据公式(7)计算粒子的惯性权重;如果σ2ε,转至step4;否则转至step6。 step4执行遗传操作(选择、交叉、变异)。 step5将初始种群与经过操作的种群合并,根据公式(8)计算粒子之间的海明距离,通过小生境淘汰策略选择适应度最好的N个粒子。 step6更新粒子的速度和位置;计算各粒子的适应度值,存储pbest(i)和gbest。 step7判断算法是否满足终止条件;若满足,则转至step8;否则转至step2。 step8输出gbest。 为了测试此改进算法的有效性,选取以下6个函数测试算法性能,其中既有简单的单峰函数,又有复杂的非线性多维函数和病态函数。测试函数详细信息见表1。为体现出改进算法优势,选取基本PSO算法、线性递减权重粒子群算法(LDWPSO)、混沌搜索粒子群算法(CLSPSO)、自然选择粒子群算法(NPSO)和遗传算法(GA)进行对比仿真实验。 表1 测试函数 函数取值范围最优值Rosenbrock[-10,10]0Rastrigrin[-5.12,5.12]0Griewank[-100,100]0Ackley[-100,100]0Sphere[-100,100]0Quatic[-1.28,1.28]0 算法设置参数为:学习因子c1=2,c2=2;wmax=0.9,wmin=0.4。对每个测试函数进行30次寻优,算法的3种统计特性如表2、表3所示。Best表示最优适应度,Mean表示适应度均值,Std表示适应度标准差。 表2 6种算法运行结果对比(D=10,MaxGen=1000) 函数统计特性RosenbrockRastrigrinGriewankAckleySphereQuaticPSOBest2.24E-51.993.20E-24.16E-41.91E-112.50E-3Mean1.643.296.73E-22.832.99E-87.80E-3Std2.111.414.53E-26.647.05E-84.90E-3LDWPSOBest6.40E-32.982.22E-21.164.25E-303.10E-3Mean2.146.697.30E-27.701.75E-181.10E-2Std1.992.173.20E-29.345.25E-188.70E-2NPSOBest1.36E-61.994.30E-21.94E-53.21E-181.20E-3Mean0.903.986.87E-24.357.07E-155.63E-3Std1.371.411.10E-27.881.40E-143.30E-3CLSPSOBest2.72E-51.992.11E-22.17E-77.00E-171.90E-3Mean7.62E-22.755.83E-20.101.93E-152.88E-2Std9.90E-20.771.90E-20.312.68E-153.10E-2GABest0.242.130.125.92E-45.95E-102.16E-2Mean1.383.350.188.30E-31.98E-83.40E-2Std0.821.187.40E-25.70E-32.07E-89.00E-3NDWNPSOBest1.91E-54.19E-83.50E-66.52E-57.97E-331.10E-3Mean2.93E-30.101.34E-41.73E-45.54E-266.09E-3Std4.21E-30.512.90E-41.08E-41.66E-253.12E-3 表3 6种算法运行结果对比(D=30,MaxGen=5000) 函数统计特性RosenbrockRastrigrinGriewankAckleySphereQuaticPSOBest29.3912.941.89E-41.516.08E-51.65E-2Mean49.5315.251.93E-214.849.90E-34.10E-2Std19.151.611.97E-29.202.99E-41.43E-2LDWPSOBest66.5425.101.90E-22.733.10E-45.46E-2Mean85.3032.733.00E-216.839.90E-47.90E-2Std11.134.748.00E-36.906.00E-41.60E-2NPSOBest19.7913.931.23E-23.60E-33.16E-51.00E-2Mean22.8016.902.26E-214.101.91E-41.98E-2Std1.903.247.80E-39.102.09E-46.10E-3CLSPSOBest18.7013.192.60E-72.90E-34.31E-55.70E-2Mean21.0017.103.33E-28.383.06E-40.13Std1.662.683.50E-210.062.50E-44.50E-2GABest18.7721.662.29E-415.431.28E-50.14Mean21.6126.142.36E-218.101.81E-40.17Std2.099.511.90E-21.531.90E-42.10E-2NDWNPSOBest1.00E-43.971.22E-104.98E-55.05E-61.30E-2Mean1.17E-24.621.31E-25.02E-41.72E-53.10E-2Std1.37E-20.601.69E-24.38E-41.35E-51.39E-2 图2 Rosenbrock函数进化曲线 图3 Rastrigrin函数进化曲线 图4 Ackley函数进化曲线 图5 Griewank函数进化曲线 图6 Sphere函数进化曲线 图7 Quatic函数进化曲线 本文算法主要是对惯性权重的调整和全局寻优能力方面进行了改进,对比的结果表明了本文改进算法的有效性;尤其是面对复杂的非线性多峰函数时,本文算法能够跳出局部最优解,搜索到全局最优解。 Sphere函数和Quatic函数为简单的单峰函数。从表2和表3中可以看出几种算法都能以很快的速度搜索到最优值,在相同迭代次数下,本文改进优化算法收敛精度较好。 其他4个函数相对于前2个函数来说比较复杂,一般的算法在对这类函数进行寻优时容易陷入局部最优解,从表2和表3中可以看出,使用小生境策略跳出局部最优解是可行的。由于改进算法将小生境策略嵌入到改进粒子群算法中,使得种群多样性大大增加,算法的后期性能得到改善。从表中可以看出,其他几种算法容易陷入局部最优解,本文改进算法在一定程度上能够使算法跳出局部最优解。 从图2~图7和表中可以看出改进的粒子群算法不管是求解单峰函数还是多峰函数都有很好的性能,尤其是面对容易陷入局部最优解的非线性复杂函数时,本文改进算法较其他2种算法在性能方面有了很大提高。 本文针对粒子群算法在处理非线性复杂函数优化方面的不足,提出了将变形的Sigmod函数作为自适应惯性权重调整公式的基函数。改进算法具有如下特点:1)引入非线性权值调整公式,在算法前期保证进化速度较快,在算法后期能够有可能拥有较大的惯性权重跳出局部最优解。2)在处理非线性多维复杂函数优化方面,引入小生境遗传算法作为算法跳出局部最优解、寻求全局最优解的关键。3)以单峰函数和多峰函数作为测试函数,通过对比其他几种算法性能,发现改进算法不管是在全局最优解的寻求还是在算法收敛速度和精度上均展现出了较好的性能。 结果表明,改进的自适应惯性权重粒子群算法既兼顾了算法的收敛速度和收敛精度,在多峰函数的寻优上也体现出了较好的性能。因此,改进算法可用于高维非线性复杂问题的求解。 参考文献: [1] Kennedy J, Eberhart R C. Particle swarm optimization[C]// Proceedings of IEEE International Conference on Neural Networks. 1995:1942-1948. [2] Shi Y H, Eberhart R C. A modified particle swarm optimizer[C]// Proceedings of IEEE Congress on Eveolutionary Computation. 1998:69-73. [3] Shi Y H, Eberhart R C. Parameter selection in particle swarm optimization[C]// The 7th International Conference on Evolutionary Programming VII. 1998,1447:591-600. [4] 敖永才,师奕兵,张伟,等. 自适应惯性权重的改进粒子群算法[J]. 电子科技大学学报, 2014,43(6):874-880. [5] 王传飞,韦涛,孙建芳. 改进粒子群算法求解广义Usher油田开发动态预测模型[J]. 新疆石油地质, 2012,33(1):102-105. [6] Zhang Jianhua, Yang Shaozeng. A novel PSO algorithm based on an incremental PID controlled search strategy[J]. Methodologies and Application, 2016,20(3):991-1005. [7] 张宏伟,张向锋,朱晨煊. 一种含驻留粒子的改进粒子群算法[J]. 计算机与现代化, 2017(11):1-5,12. [8] 董立军,蒲亦非,周激流. 基于多尺度分数阶多重记忆与学习的粒子群算法[J]. 计算机应用研究, 2018,35(3):1-2. [9] 刘爱军,杨育,李斐,等. 混沌模拟退火粒子群优化算法研究及应用[J]. 浙江大学学报(工学版), 2013,47(10):1722-1730. [10] 赵志刚,林玉娇,尹兆远. 基于自适应惯性权重的均值粒子群优化算法[J]. 计算机工程与科学, 2016,38(3):501-506. [11] Comak E. A generalized particle swarm optimization using reverse direction information[J]. Turk J Elec Eng & Comp Sci, 2016,24(2):639-655. [12] 郑金华,罗彪. 一种基于拉丁超立方体抽样的多目标进化算法[J]. 模式识别与人工智能, 2009,22(2):223-233. [13] He Yan, Ma Weijin, Zhang Jiping. The parameters selection of PSO algorithm influencing on performance of fault diagnosis[C]// 2016 International Conference on Mechatronics, Manufacturing and Materials Engineering. 2016. [14] 李佳,刘天琪,李兴源,等. 改进粒子群-禁忌搜索算法在多目标无功优化中的应用[J]. 电力自动化设备, 2014,34(8):71-77. [15] 马松涛. 复杂优化问题中小生境粒子群优化算法的改进及研究[D]. 郑州:郑州大学, 2013. [16] Gong Yuejiao, Li Jingjing, Zhou Yicong. Genetic learning particle swarm optimization[J]. IEEE Transactions on Cybernetics, 2016,46(10):2277-2290. [17] 谢红侠,马晓伟,陈晓晓,等. 基于多种群的改进粒子群算法多模态优化[J]. 计算机应用, 2016,36(9):2516-2520.2.4 非线性动态调整惯性权重小生境粒子群算法(NDWNPSO)
3 仿真分析
3.1 测试函数
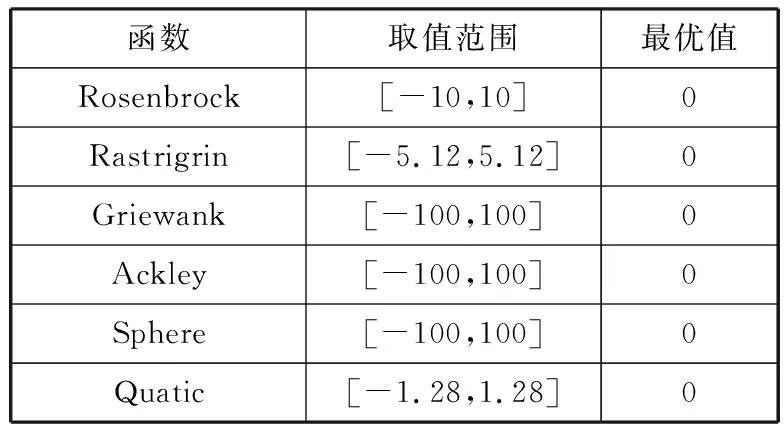
3.2 仿真结果及分析
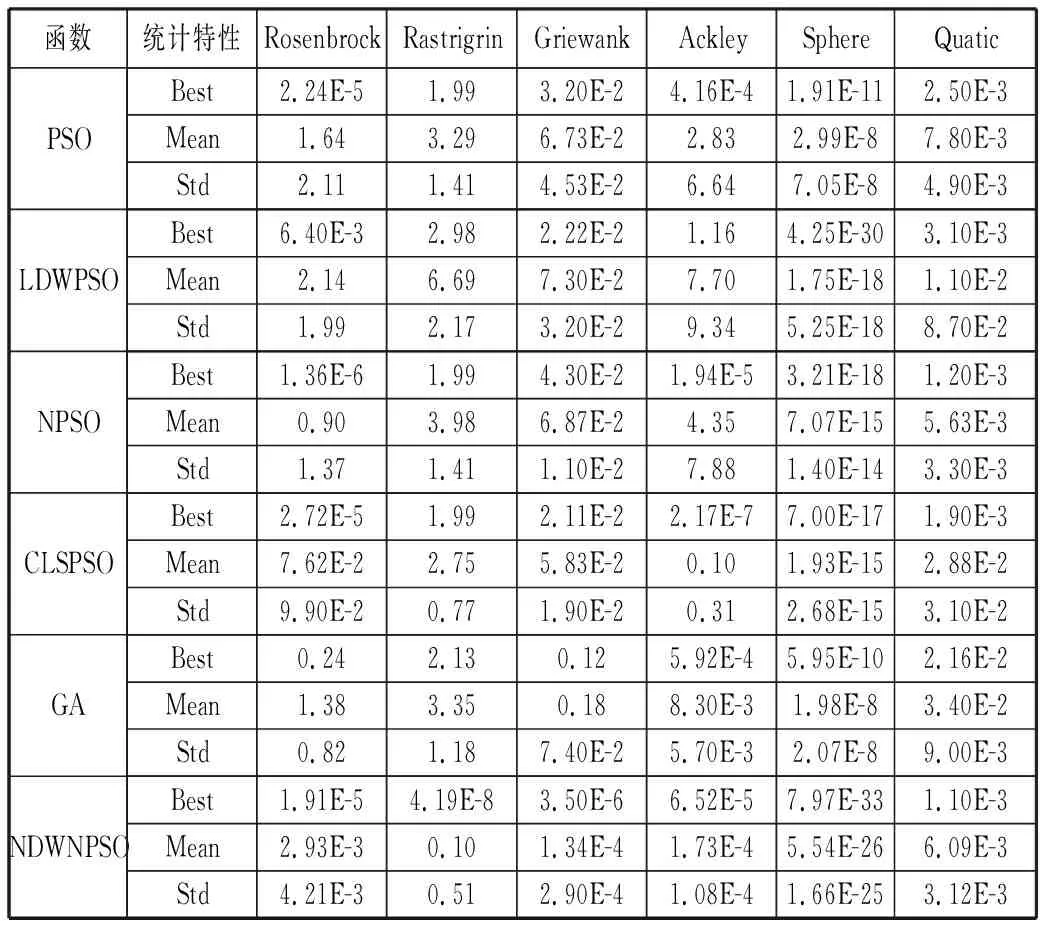



4 结束语
