基于SBT全结点存储的云数据完整性
2018-06-28龙士工
周 鹏,龙士工
(1.贵州大学计算机科学与技术学院,贵州 贵阳 550025; 2.贵州省公共大数据重点实验室,贵州 贵阳 550025)
0 引 言
随着分布式计算机硬件处理能力和网络传输能力的提升,远程数据处理中心能够给用户提供高质量的数据和软件服务。云计算就在这种情况下应运而生了,它是继网格计算、对等计算、分布式计算之后的又一种新型计算模式,其核心理念是按需服务、按用收费,为用户提供随处可用的资源连接池。通过云计算技术,不仅使得用户和企业可以随时随地通过网络访问自己的资源,同时减少了在软硬件管理上的投入。云计算强大的计算能力和存储能力使得用户更愿意将复杂的任务交付给云平台处理,然而当用户将大量的数据部署到云平台时,云计算系统就演变成一个云存储系统,使得用户用低廉的价格就能获得海量的存储能力,但是高度集中的计算机资源给云存储带来了严峻的安全挑战。根据Gartner调查结果显示,曾经70%受访企业的CEO担心云数据隐私被侵犯而拒绝大量使用云计算模式。而在最近几年,各大云服务提供商也相继暴露出安全问题,如谷歌Gmail邮箱故障和盛大云机房物理服务器磁盘故障。
在现有的完整性验证方案中由于自身原因存在着较大的局限性,如早期Deswarte等人[1]提出基于MAC认证码验证机制,后来又在此基础上做出改进,利用同态特性(am)=arm=(ar)m,提出了基于RSA签名完整性验证机制以及Dan等人[2]提出的基于BLS的短签名机制。上述方案中都在通讯效率和计算代价上做了改进,但是都仅针对静态数据存储,并不能支持动态数据更新,无法适应动态环境。因此,Ateniese等人[3]最先开始考虑如何支持动态操作,对现有方案做出改进,提出了支持部分动态更新的验证机制,但不能进行数据插入操作。基于这个问题,Erway等人[4]提出了基于跳表的验证机制来支持插入操作,但其认证路径过长,每次需要大量的辅助信息支持,计算代价和通讯开销较大。后来又提出了一种以Merkle-Tree数据结构为基础的方案[5-6],该方案中存储数据集为S,将S中的元素存储在Hash树的叶子结点中,并且每个结点都存储一个标签值。如果该结点为叶子结点,其标签值与其存储的数据相同;否则其孩子结点的标签值就需要通过抗碰撞哈希函数计算得出。而用户保存数据集S的摘要值就是Merkle-Tree根结点的摘要值。相比跳表具有更简单的数据结构,但是造成存储空间的极大浪费。文献[18]中将树形结构与RSA技术相结合构造出一种RSA树,该方案引入参数ε使得树的高度和树的分支都为常量,因此,该方案中得到的证据大小、查找和验证的时间复杂度为O(l)。但是该方案采用了单向累加技术,需要使用复杂的幂运算,所以实际的运行时间并不乐观,并且RSA树在大量数据插入操作上并不灵活,还会导致复杂的结构重构问题。
基于上述完整性认证方案所存在的不足,从存储空间和通信效率角度出发,并与现有方案相结合,本文引入了一种平衡二叉搜索树的数据结构——结点大小平衡树(Size Balance Tree, SBT),二叉排序树的结构特点使得数据的查找非常高效,可以快速定位到目标结点;同时平衡二叉树的结构特点又能够很好地维持树的高度以至不退化为链表,保证了数据查找和更新的效率。
1 云存储环境下的数据完整性证明
1.1 数据存储模型
云存储环境下的体系架构一般基于2种基础模型,分别为两方模型和三方模型。三方模型即引入了可信第三方审计(Third Party Auditor, TPA),具有更多的审计经验和能力,替代用户对云存储中的数据执行审计任务,也减轻了在验证阶段用户所需要的计算负担。其结构关系如图1所示。
在三方模型中,由于接入云中的设备受到计算资源的限制,用户不可能将大量的时间和精力花费在对云数据的完整性检测上,往往将其交付给经验丰富的第三方来完成。因此,验证方只需要拥有少量的公开信息即可完成完整性验证。而在两方模型中,没有第三方审计,只有云存储用户和云服务提供商,用户本身就具有三方模型中的审计功能。由于在这2种存储模型中,三方模型的自身优势更符合云存储的特性,所以本文中对云存储环境下的数据完整性研究,都是基于三方模型展开。

图1 云环境下存储模型
1.2 构建框架
数据完整性证明机制由Setup和Challege这2个阶段构成,通过随机数据抽样的方式对云存储中数据进行完整性验证。具体实现由如下4个多项式时间算法组成:
1)keyGen(1k)→(pk,sk)。密钥对生成算法,由用户来执行。算法以安全参数k作为输入,输出密钥对(pk,sk)作为返回值。
2)TagBlock(sk,f)→η。数据块标签生成算法,由用户来执行。算法以私钥和文件f作为输入,将每个文件生成的标签集合η输出作为认证的元数据。
3)GenProof(pk,f,η,chal)→ρ。证据生成算法,该算法在服务器上运行。将用户公钥pk、文件f、认证的标签集合η以及用户的挑战请求chal作为输入,生成这次请求的验证证据ρ返回。
4)CheckProof(pk,ρ,chal)→(″true″,″false″)。证据验证算法,由可信第三方TPA执行。该算法将用户的公钥pk、服务器生成的证据ρ以及用户挑战请求chal作为输入参数返回验证成功或者失败。
上述算法在数据完整性证明机制具体实施过程中可以分为2个阶段:Setup阶段和Challege阶段。
1)Setup阶段:初始化阶段。用户首先运行keyGen(·)算法生成密钥对(pk,sk);然后对文件f分块,执行TagBlock(·)算法为每个数据块fi生成标签集合η={ηf1,ηf2,…,ηfn};最后将数据文件f和标签集合η发送给云服务器,删除本地{f,η}。
2)Challege阶段:用户挑战请求阶段。可信第三方作为TPA向云服务器周期性地发起完整性验证。从文件f中随机选取c个数据块{f1,f2,…,fc}生成挑战请求chal发送给云服务器。
服务器作为证明者,通过存储在服务器上的{f,η},执行GenProof(·)生成验证证据ρ返回给验证者,TPA作为验证者收到证据后,执行CheckProof(·)验证证据是否正确。
2 基于SBT全结点存储的数据完整性方法
2.1 结点大小平衡树——SBT
2.1.1 SBT的结构
SBT本身也是一棵二叉排序树,其性质如下:
1)若左子树非空,则左子树上的所有结点关键字值均小于根结点的关键字值。
2)若右子树非空,则右子树上的所有结点关键字值均大于根结点的关键字值。
3)左、右子树本身也分别是一颗二叉排序树。
其又具备了平衡二叉树的特点。为了避免树的高度增长过快,降低二叉排序树的性能,规定在插入和删除操作时,保证任意结点的左、右子树高度差绝对值不超过1。它的优点是可以高效动态地维护二叉排序树的高度,如果树中出现结点不平衡的情况,需要进行左旋或右旋操作来保持平衡,并且旋转操作不需要额外的存储空间。
SBT中的平衡性是通过其定义的结点大小,即以该结点为根的结点的个数之间的关系来维持的。其结构如图2所示。

图2 SBT结构图
SBT树中的每一个结点应满足如下性质:
1)s[left[A]]≥s[right[right[A]]],s[right[left[A]]]
2)s[right[A]]≥s[left[left[A]]],s[left[right[A]]]
其中s[A]指的是以结点A为根的子结点的个数,left[A]指的是A的左孩子,right[A]指的是A的右孩子。在图2中该性质体现为:
s[L]≥s[D],s[E]& s[R]≥s[B],s[C]
如果在SBT上进行删除或者插入操作后,可能导致SBT上结点不满足上述性质,则需要执行Maintain()函数以调整树的高度来维持树的平衡。
以图2中SBT为例,假如出现s[B]>s[R]的情况,则需要通过以下步骤对其进行修复:
1)首先对根结点A进行右旋转Right-Rotate(A)操作,使得SBT由图2转化为图3。
2)右旋操作后可能还会出现s[D]>s[C]或者s[E]>s[C],同样不满足上述性质,所以还需要对A执行Maintain()操作;
3)图3中L的右子树可能由于步骤2中的不断调整出现不满足性质的情况,因此最后还需要对L执行Maintain()操作。
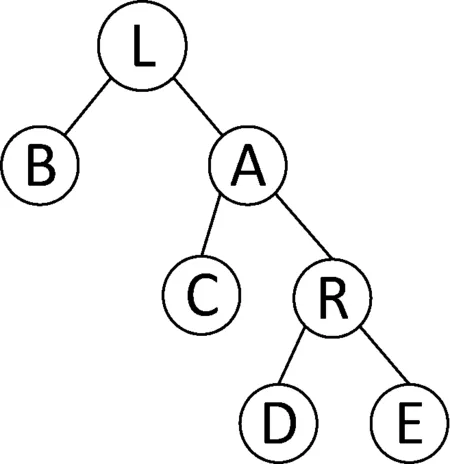
图3 右旋A后结构图
2.2 数据结构可认证化
基于SBT结构构建起来的全结点存储树A中每个结点都存储着如下3个字段:
1)该结点中存储的数据Dv4。
2)该结点数据的摘要值Hv=h(Dv4)。
3)该结点上的联合摘要值Hsum(v):如果该结点为底层叶结点,则Hsum=Hv;若该结点中只存在右孩子结点,则Hsum=h(Hv,Hsum(v.getLeft));如果该结点只存在左孩子结点,则Hsum=h(Hv,Hsum(v.getRight));如果该结点左孩子和右孩子结点都存在,则Hsum=h(Hv,Hsum(v.getLeft),Hsum(v.getRight))。

图4 可认证的SBT结构示意图
云存储环境中某个数据集的哈希摘要值为Digest(A),即在验证过程中用来进行对比的摘要值,就是该结点大小平衡树的联合摘要值。一个可认证的结点大小平衡树结构示意图见图4
2.3 验证过程
当用户发送一个检测数据请求到云服务器时,假如服务器在全结点存储树中找到存储着目标数据对应的目标结点target时,并且服务器会记录root到target的查找路径path={v0(target)→v1→…→vl-1→vl(root)}。此时,服务器还会给审计第三方TPA返回Yes并返回相应的证据ρ={η,λ1,λ2,…,λl}。其中η的定义如下:
1)如果v0是叶子结点,则η={Dv0}。
2)如果v0不是叶子结点,则η={Dv0,Hsum(v0.getLeft),Hsum(v0.getRight)}。
λ的定义如下:
1)如果vi-1为左孩子结点,则λi={Hvi,Hsum(vi-1),Hsum(vi.getRight)}。
2)如果vi-1为右孩子结点,则λi={Hvi,Hsum(vi.getLeft),Hsum(vi-1)}。
以图4所示的可认证的SBT为例,如果需要验证的数据块为Dv4,则证据ρ生成信息示例如图5所示。
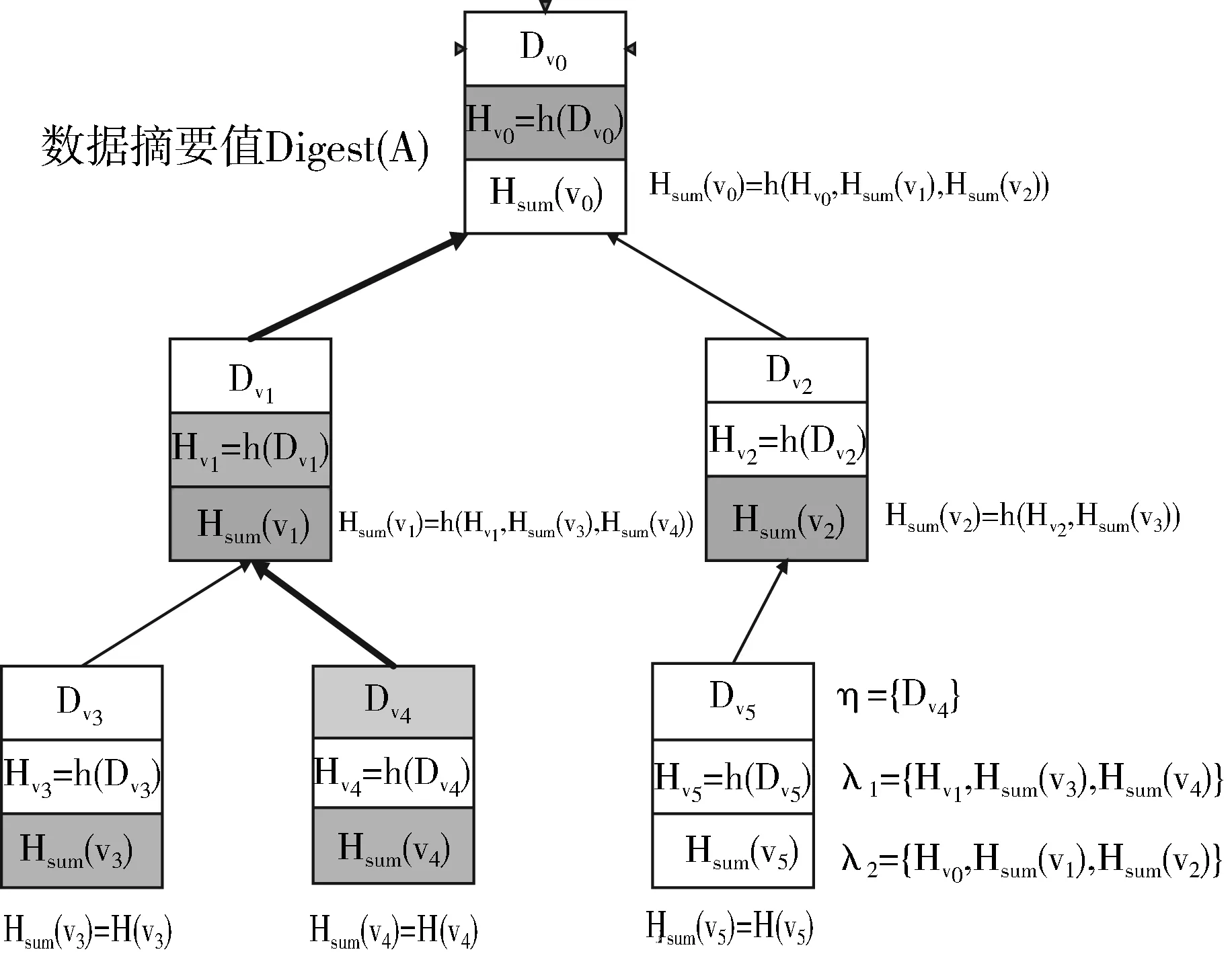
图5 证据ρ生成示意图
当可信第三方TPA收到云服务器返回的证据ρ时,将进行如下验证过程:
1)计算目标结点v0的摘要值,即a=h(Dv0),如果v0是叶子结点,则验证a=Hsum(Dv0)是否成立;否则,验证h(a,Hsum(v0.getLeft),Hsum(v0.getRight))=Hsum(v0)是否成立。
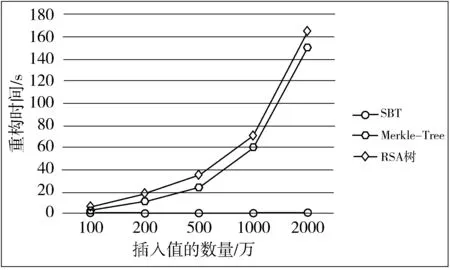
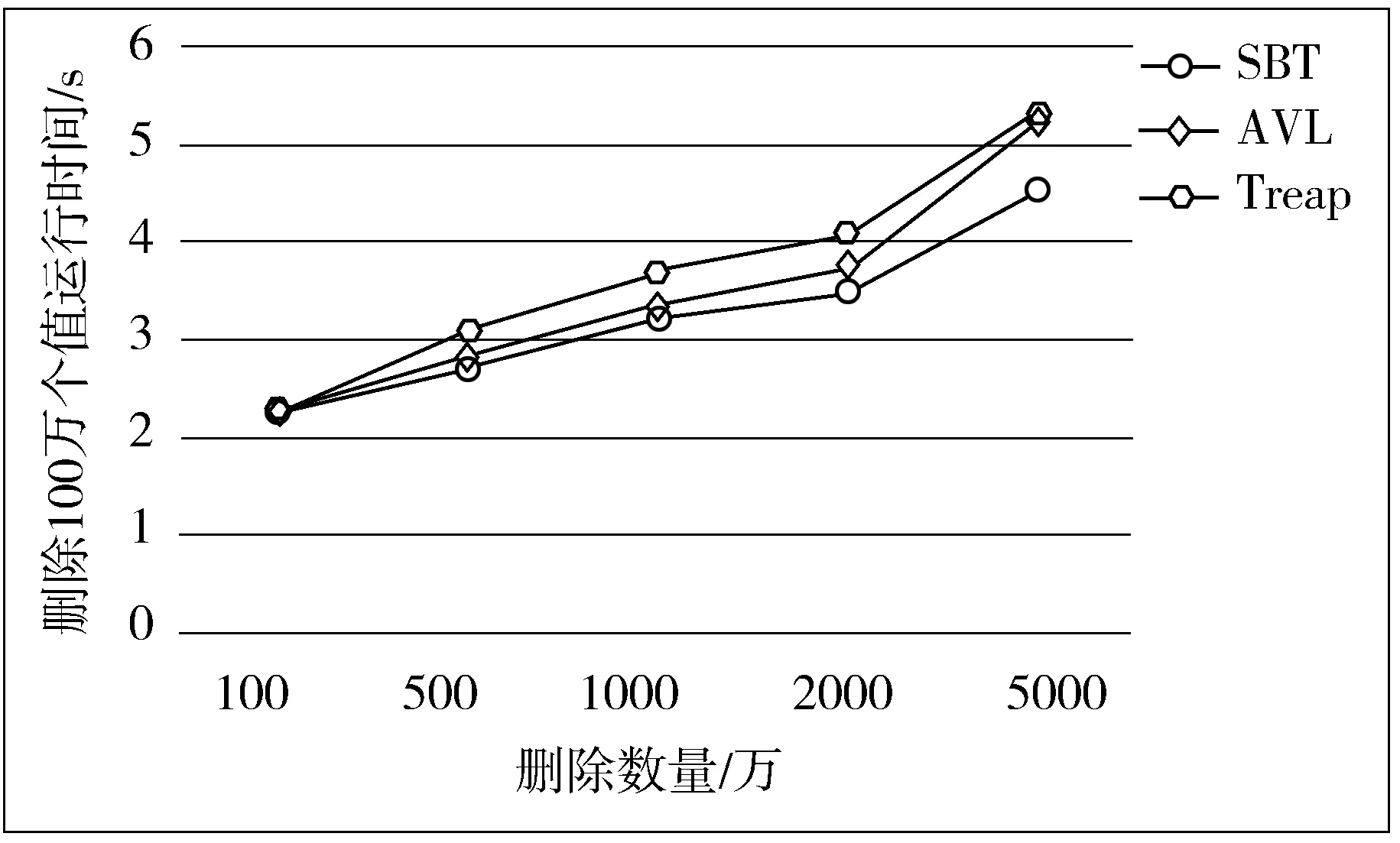
2)对于路径中的某个结点vi,即λi(i 3)对于根结点vl,即λl,同理如果vi-1为根的左孩子结点则计算h(Hvl,Hsum(vl-1),Hsum(vl.getRight));否则计算h(Hvl,Hsum(vl-1),Hsum(vl.getLeft));并与用户之前发送给TPA的数据摘要值Digest(A)作比较。 图6 完整性验证过程示意图 如果上述验证过程全部成立,则证明云服务器返回的证据ρ是正确的,即所查询的数据是完整的;否则,用户就会认为该数据已被修改或者伪造,此时就需要采取数据恢复技术对云存储中的数据进行恢复操作。 以图5结构为例,其数据完整性验证过程如图6所示。 通过上述分析,可得到如下结论: 1)对于查询验证操作,SBT认证及Merkle-Tree认证算法的时间复杂度在同一数量级,均为O(logn)。而与RSA树认证相对比,这2种认证方案都使用了哈希函数替代复杂的模幂运算,因此计算上更加简单。 2)在支持动态数据集方面,Merkle-Tree认证采用2-3树支持动态数据集,而RSA树认证是将成员哈希分组为固定大小的Bucket来支持动态数据集。因此这2种方式都不可避免地导致了认证结构的周期性重构。 3)SBT结构具有良好的自平衡性,能够有效地控制树高,使其趋近于完全二叉树。二叉树上的查询和更新操作时间复杂度都和树高有关,相对于非平衡树而言,SBT结构在数据操作效率上大大提高,将时间复杂度维持在O(logn)。此外,SBT认证也可以完全避免认证结构周期性重构。针对上述方案在插入操作中的重构分析,分别对SBT、Merkle-Tree、RSA树插入100万、200万、500万、1000万以及2000万个随机值,重构时间统计如图7所示。 图7 重构时间统计图 因此,对于大规模并且需频繁更新的数据集,该方案具有明显的优势。为了验证该树形结构更适合构建数据认证,下面通过实验将SBT与AVL树、Treap进行比较,评估基于SBT全结点存储云数据完整性验证方案中查询和更新的时间复杂度。 图8 插入操作时间统计图 针对基于SBT上插入操作分析,在SBT、AVL和Treap结构中分别插入100万、500万、1000万、2000万以及5000万个随机值,时间统计见图8。 图9 删除操作时间统计图 针对基于SBT上删除操作分析,在具有100万、500万、1000万、2000万以及5000万个随机值的SBT、AVL和Treap结构中,分别删除100万个值所用时间,删除操作时间统计如图9所示。 针对基于结点大小二叉树上的查询验证操作的时间分析,在具有100万、500万、1000万、2000万以及5000万个随机值的SBT、AVL和Treap结构中分别查询100万个目标值运行结果时间统计如图10所示。 图10 查询验证操作平均时间统计图 对于用户向云服务器发送验证请求时,服务器在生成证据信息过程中,没必要进行数据摘要值的重新计算,只需要在认证化的SBT中找到相应的数据结点,并把根结点到该目标结点路径上的结点摘要值及其子结点和兄弟结点作为返回值,返回的摘要值的个数与SBT的高度之间呈线性关系。可信第三方TPA在对返回的证据进行验证时,仅需进行O(logn)次哈希计算即可。 基于SBT认证的安全性与基于Merkle-Tree的认证相同,其安全性保证都是以其哈希函数的抗碰撞性为基础实现。 目前,云计算的优势使得越来越多的企业和个人更愿意将数据交付到平台处理,这给云存储的普及带来了非常可观的发展前景,然而数据本身的不确定性以及云服务器的不完全可信又使得云存储下的数据安全难以得到保障。针对数据完整性验证问题,本文提出了一种基于SBT全结点存储的数据完整性验证方案,并详细地介绍了云存储下完整性验证框架和基于结点大小平衡树全结点存储的数据验证过程。全结点存储相比叶结点存储无疑减少了服务器上的存储开销,也降低了树的高度,再者SBT本身具有二叉排序树和二叉平衡树的结构特性,不仅使得数据查找时非常高效,同时又很好地维持了树的高度,也保证了数据更新操作时的效率。 参考文献: [1] Deswarte Y, Quisquater J J, Saïdane A. Remote integrity checking[M]// IFIP International Federation for Information Processing. Springer, 2004,140. [2] Dan B, Lynn B, Shacham H. Shortsignatures from the weil pairing[M]// Advances in Cryptology—ASIACRYPT 2001. Springer Berlin Heidelberg, 2001:514-532. [3] Ateniese G, Pietro R D, Mancini L V, et al. Scalable and efficient provable data possession[C]// Proceedings of the 4th International Conference on Security and Privacy in Communication Netowrks. ACM, 2008:1-10. [4] Erway C, Papamanthou C, Tamassia R. Dynamic provable data possession[C]// ACM Conference on Computer and Communications Security. 2009:213-222. [5] Merkle R C. A certified digital signature[J]. Lecture Notes in Computer Science, 1990,435:218-238. [6] Merkle R C. Protocols for public key cryptosystems[C]// Proceedings of IEEE Symposium on Security and Privacy. 1980,3:122. [7] 任化强. 云环境下操作外包的动态审计方案设计与实现[D]. 成都:电子科技大学, 2016. [8] 邓晓鹏,马自堂,高敏霞,等. 一种基于双线性对的云数据完整性验证算法[J]. 计算机应用研究, 2013,30(7):2124-2127. [9] 李莹,张永胜,马洁. 一种基于H-MHT的动态数据完整性检查方案[J]. 计算机应用研究, 2015,32(12):3710-3713. [10] 张亮. 云存储数据完整性检测技术研究[D]. 大连:大连理工大学, 2014. [11] 谭霜,贾焰,韩伟红. 云存储中的数据完整性证明研究及进展[J]. 计算机学报, 2015,38(1):164-177. [12] 秦志光,王士雨,赵洋,等. 云存储服务的动态数据完整性审计方案[J]. 计算机研究与发展, 2015,52(10):2192-2199. [13] 姚戈. 云存储数据完整性验证机制研究[D]. 北京:北京交通大学, 2016. [14] 赵宇龙. 云存储中第三方审计机构在数据完整性验证中的应用[D]. 成都:电子科技大学, 2015. [15] 杜朝晖,王建玺. 云存储中利用TPA的数据隐私保护公共审计方案[J]. 电子技术应用, 2015,41(5):123-125. [16] 邢建川,韩帅. 一种基于哈希树的数据动态操作可验证性方法: 中国, CN103218574A[P]. 2013-07-24. [17] Motghare S, Khandait S P, Mohod P S. Framework of data integrity for cross cloud environment using CPDP scheme[J]. International Journal of Advanced Research in Computer Science, 2013,4(2):55. [18] Papamanthou C, Tamassia R, Triandopoulos N. Authenticated hash tables based on cryptographic accumulators[J]. Algorithmica, 2016,74(2):664-712. [19] Rao S, Gujrathi S, Sanghvi M, et al. Analysis on data integrity in cloud environment[J]. IOSR Journal of Computer Engineering, 2014,16:71-76.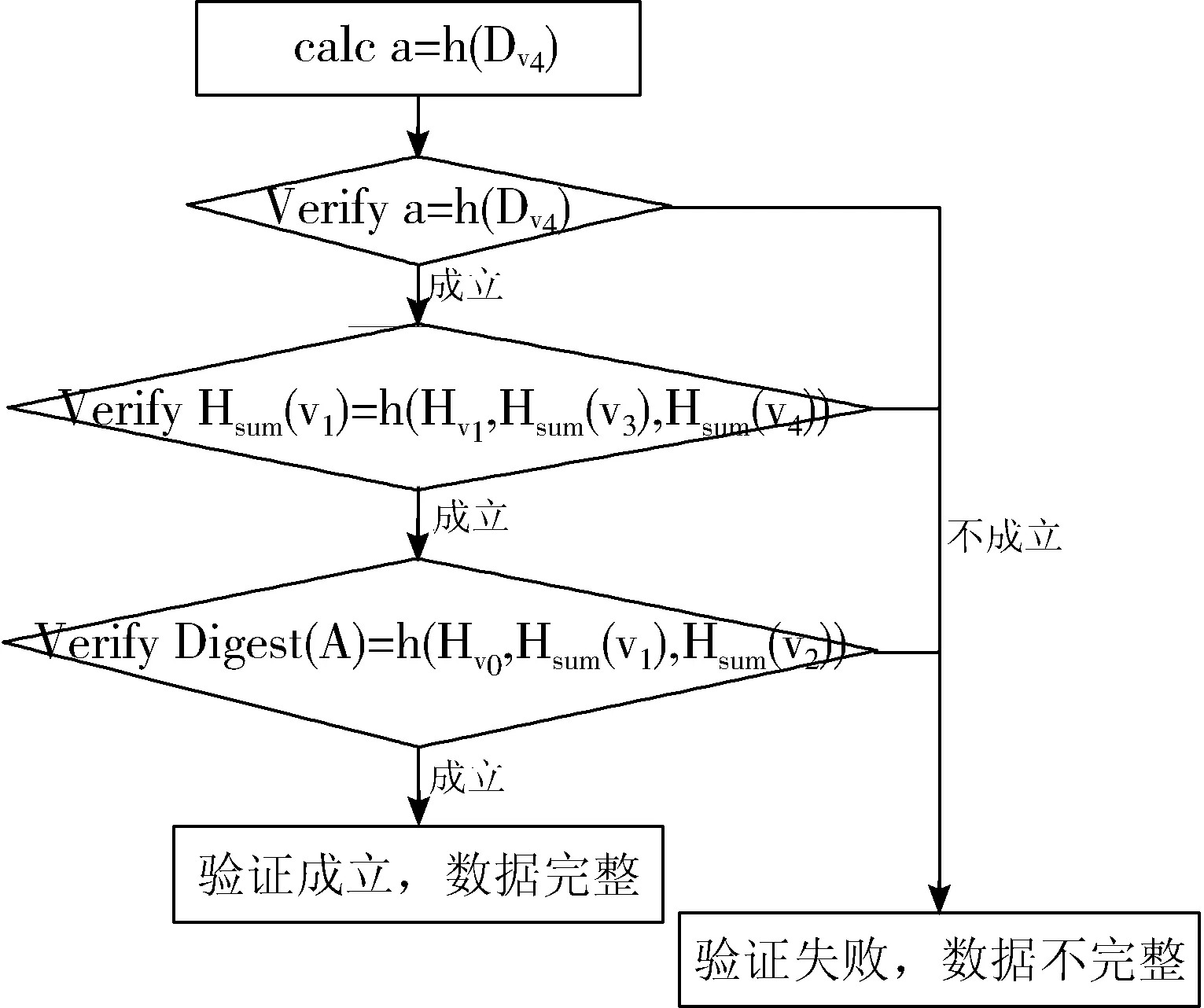
3 结果分析
3.1 数据更新操作分析

3.2 验证过程分析

3.3 安全性分析
4 结束语
