基于改进参考点的快速非支配排序遗传算法研究
2018-06-28肖俊明刘凯松朱永胜高洪洋
肖俊明, 刘凯松, 朱永胜, 谢 亮, 高洪洋
(中原工学院 电子信息学院, 河南 郑州 450007)
近年来,高维多目标优化问题成为进化计算的研究热点及难点。为改善高维多目标优化问题,1980年, Wierzbicki A P最先提出了一种参考点方法,其目的是通过求解一个成就标量问题得到一个最接近理想参考点的Pareto最优解[1]。Deb K等在Evolutionary Multi-objective Optimization(EMO)中使用参考点方法,结合决策者偏好信息找到了一组Pareto最优解集[2]。Mohammadi A等结合分解策略与参考点方法来搜索优选区域[3]。Figueira J R等通过近似Pareto前沿的并行策略来生成参考点,使用多个参考点将目标空间均匀地分割成不同的区域,对于每个参考点,独立地找到一组近似有效的解,以便同时计算[4]。Wang R等提出了一种偏好启发共同进化算法(Preference-inspired Co-evolutionary Algorithm,PICEA),以便在进化过程中同时优化候选解决方案和参考点,即通过较少的候选解决方案使参考点获得更高的适应度,通过满足尽可能多的参考点使候选解决方案获得适应性[5]。Deb K等根据当前种群获得了覆盖整个目标空间的超平面,并在超平面上生成一系列分布均匀的参考点[6]。本文对参考点的策略进行了改进,并将其与快速非支配排序遗传算法(NSGA-Ⅱ)相结合,形成了基于改进参考点的快速非支配排序遗传算法。
1 快速非支配排序遗传算法
以最小化为例,假设一个具有m维目标函数、n维决策变量的多目标优化问题,其表达式为[7]:
(1)
其中:x是决策变量,X是n维决策空间,F(x)为m维目标函数向量。当目标维数m≥4时,F(x)即为高维多目标函数,此问题即为高维多目标优化问题(Many-objective Optimization Problem)MaOP[8-9]。
Deb K等在非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm,NSGA)的基础上提出了快速非支配排序遗传算法(NSGA-Ⅱ)[10]。它的改进主要包括三方面:①采用快速非支配排序的方法,使计算复杂度大大降低;②定义了拥挤度和拥挤度比较算子,替代了需要指定的共享半径,使准Pareto域中的个体能扩展到整个Pareto域,且均匀分布,保持了种群的多样性;③引入了精英策略,扩大了采样空间,防止了最佳个体的丢失,提高了算法的运算速度和鲁棒性。NSGA-Ⅱ在处理较少目标(2个或3个)时,优化效果很好,但在优化高维多目标问题时,其优化效果将大大降低。目前存在以下问题:①有限规模的最优解无法近似高维目标空间中的Pareto前沿,算法的复杂度随目标空间维度的增加而变大;②在解决高维多目标问题时,算法的分布性能不佳;③优化较多目标时,非支配解的可视化十分困难。
2 参考点策略的改进
Liu Y等提出了基于参考点的多目标进化算法(Many-objective Evolutionary optimization based on Reference Points,RPEA)。该算法重新定义了参考点的选择方法,并加强了对Pareto前沿的选择压力,同时保持了解个体广泛和均匀的分布[11]。在RPEA算法中,根据当前群体生成了具有良好收敛性和分布性的一系列参考点,以指导个体进化。此外,算法通过计算目标空间中参考点和个体之间的Tchebychev距离[12],获得基于每个个体的评价,从而选择优良个体。RPEA的主要特征为:①提出的算法被推广到一个共同的框架;②仅利用父代和子代群体中的非支配个体来产生参考点,从而进一步增强这些参考点的性能;③采用基于Tchebychev距离的实现函数,以有效地评价候选解。其中,参考点选择策略可表示为:
r=(f1(x),…,fm(x)-ε,…,fM(x))(1≤m≤M)
(2)
改进后的参考点选择策略表示为:
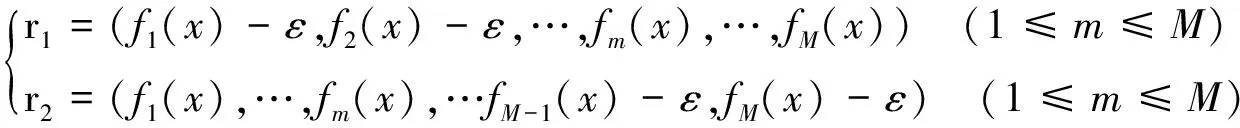
(3)
RPEA是通过公式(2)在单一目标函数上减小相应的目标值(ε是大于0的极小值)来生成参考点的,改进后的算法按照公式(3)向两个目标函数同时减小相应数值以生成参考点,这样改进后的参考点策略就进一步加强了最优前沿的选择压力。在选择新个体时,删除具有最小切比雪夫距离的个体,以避免重复选择,同时删除具有最小切比雪夫距离的参考点,以保证种群的多样性。
3 基于改进参考点的快速非支配排序算法
本文通过深入研究,将改进的参考点策略与快速非支配排序遗传算法(A Fast Elitist Non-dominated Sorting Genetic Algorithm,NSGA-Ⅱ)相结合,得到了一种可以解决高维多目标问题的基于改进参考点的快速非支配排序算法(RP-NSGA-Ⅱ)。
3.1 算法应用的操作
(1)初始化,由每一个向量(称为染色体或基因)组成问题的候选解。问题中的每个参数都有一个变量范围,且不能为负。初始化时应尽可能地覆盖全部的搜索范围。
(2)交叉操作,通过使用模拟二进制交叉算子(SBX)进行交叉操作。SBX 是一种二进制交叉算子,用来模拟在自然界中观察到的染色体交叉过程。两条父代染色体交叉生成两条子代染色体,保存于父代中染色体的相关信息在子代染色体中会得到保护。数学描述如下:
(4)
其中:ci,k表示含有第k个基因位的第i个子代;pi,k表示被选择的父代个体;βk(≥0)是具有一定概率的随机数。
(5)
公式(5)中β分布可以从(0,1)之间的均匀采样随机数u中获得。ηc为交叉点的分布指数(DIC),是非负实数,当ηc的值比较大时,子代个体与父代个体相邻的概率就比较大;而当ηc的值比较小时,子代个体与父代个体之间的距离就比较远。参数ηc可以根据实际情况进行自定义。
进化过程前期,SBX可以促使算法探索未知空间信息,到进化过程后期,算法可以利用个体信息逐渐收敛。
(3)变异操作,采用多项式变异算子(PM)进行变异操作,以防止算法陷入局部最优。其数学描述如下式:
(6)
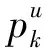
(7)
其中:rk是(0,1)之间的均匀采样随机数;ηm是自定义参数,称为变异分布指数 (DIM)。
(4)精英策略,将子代个体集合与父代个体集合相结合,生成下一代的个体。若父代和子代中最好的个体都加入过渡个体集合,则精英策略就可得到保证。根据非支配排序对过渡个体集合进行分类,随后每个最低级别的非支配集合都会填补到子代中,直到种群规模超过目前的个体规模。若种群规模大于N,则对最后加入子代种群的非支配集进行拥挤距离排序,并从中选择具有较大拥挤距离的个体,使种群规模维持在N。
(5)个体选择,根据生成的参考点指导解个体的进化过程,并选择最优解。
3.2 算法流程
RP-NSGA-Ⅱ算法流程见图1。
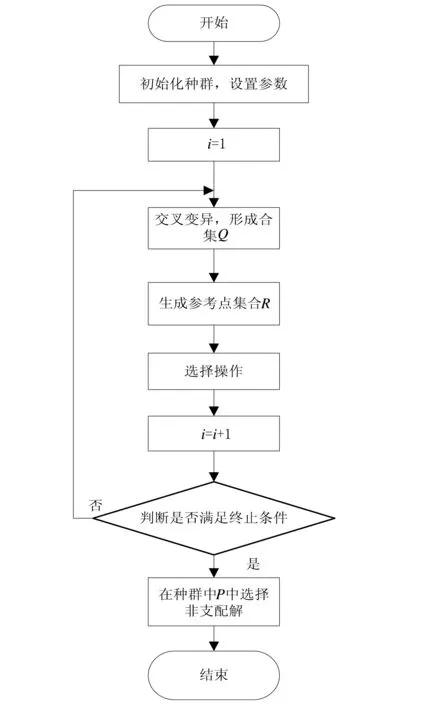
图1 算法流程图
主要算法步骤如下:
步骤1:初始化种群,设置种群大小、迭代次数等参数。
步骤2:父代种群P通过交叉、变异操作,生成相同种群大小的子代种群P′。
步骤3:对集合(P+P′)进行非支配操作,形成非支配解集Q。
步骤4:集合Q中的每个个体根据公式(3)生成参考点,将生成的参考点进行非支配排序,非支配个体为参考点集合R。
步骤5:根据切比雪夫距离公式计算个体与参考点之间的距离,选择具有最小切比雪夫距离的个体,形成子代种群P(t+1)。
步骤6:判断是否满足终止条件。若是,则进入步骤7;否则,返回步骤2。
步骤7:从子代种群中选择非支配解并输出。
4 实验分析
DTLZ是一个连续的问题函数集,可以应用到任意数量的目标和决策变量的问题中(M是目标空间维数,n是决策空间维数),并且通常将其用于多目标优化。DTLZ函数集由具有多种特性的多个问题组成,例如线性,凹面,偏置或退化的Pareto前沿。DTLZ函数集的特性见表1。
本文选择被广泛使用的Inverted Generation Distance(IGD)指标来测试改进后算法的性能。IGD可以测量解集的收敛性和多样性,IGD的值越小,算法的性能越好。测试中,将RP-NSGA-Ⅱ与经典NSGA-Ⅱ,具有参考点的RPEA和具有代表性的MOEA/D进行性能对比实验。为保证对比实验的公平性,四种算法均采用相同的参数设置:种群大小为100,目标数目为6,变量x维数为15(DTLZ1中维数为9),迭代次数为1 000。实验结果均为各算法独立运行30次所对应的平均值和标准差,其中最优结果均加粗表示。实验结果如表2所示。
表2显示,MOEA/D在解决DTLZ1时表现最佳,这是因为DTLZ1具有线性和大量局部最优的多模态问题,问题的目标值范围远大于其Pareto前沿,而MOEA/D避免了在其他算法中标准化程序容易将原始目标转化为错误尺度的问题。而DTLZ2问题比较容易解决,从实验结果可以看出RP-NSGA-Ⅱ具有更好的性能。对于DTLZ3,MOEA/D具有最佳性能。对于DTLZ4,RPEA显著优于其他算法,表明该算法具有很强的解决不规则Pareto阵线问题的能力。对于DTLZ5和DTLZ6,RP-NSGA-Ⅱ在解决Pareto退化问题时具有最佳性能。
分析表2中的数据,RP-NSGA-Ⅱ算法的优化效果远远优于NSGA-Ⅱ算法。RP-NSGA-Ⅱ在处理Pareto问题时更优秀,但是在处理具有多模态问题时,性能略有不足。综上所述,本文提出的基于改进参考点的非支配排序算法在解决高维多目标问题时具有良好的收敛性和稳定性。
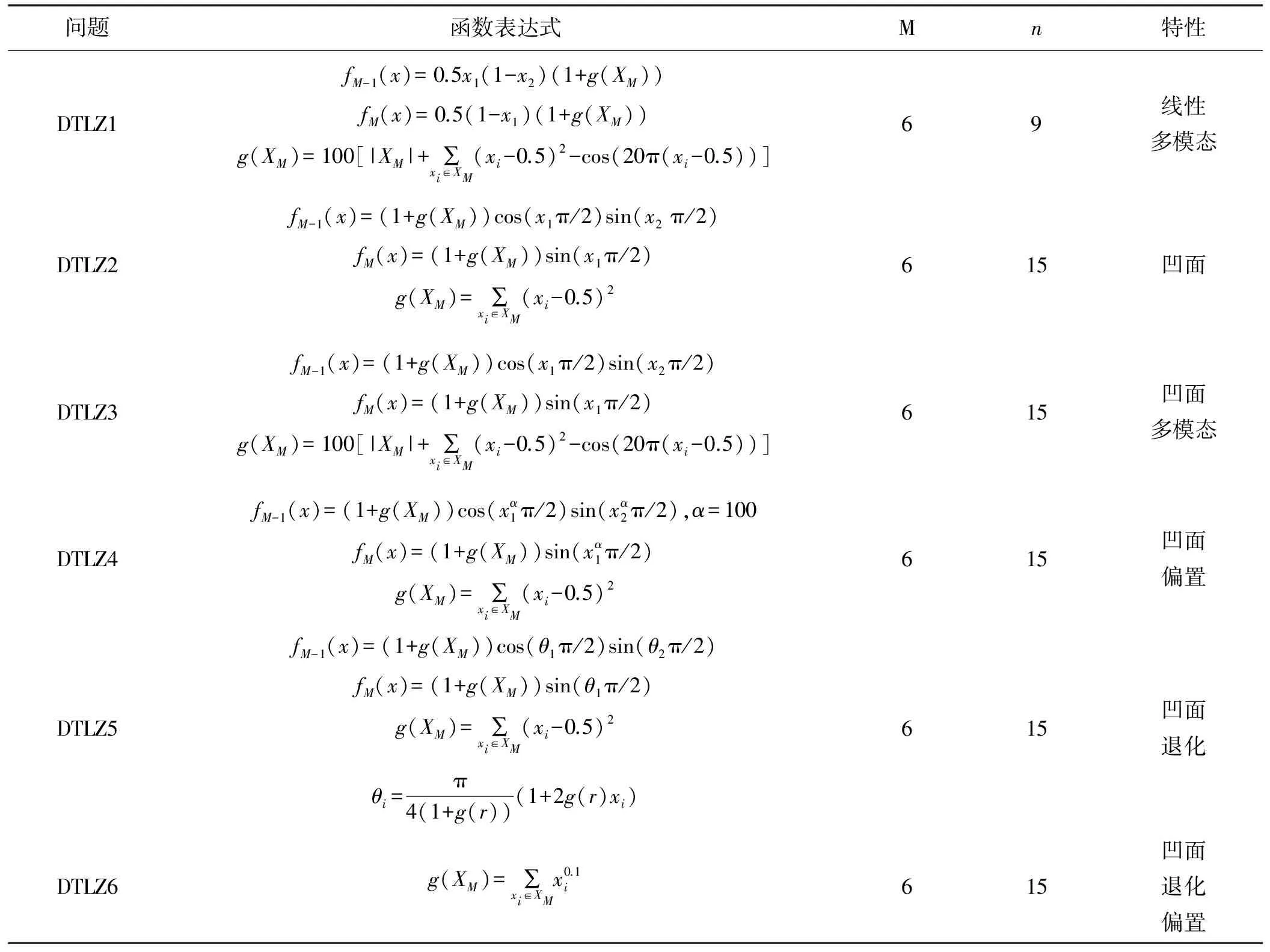
表1 DTLZ测试函数集
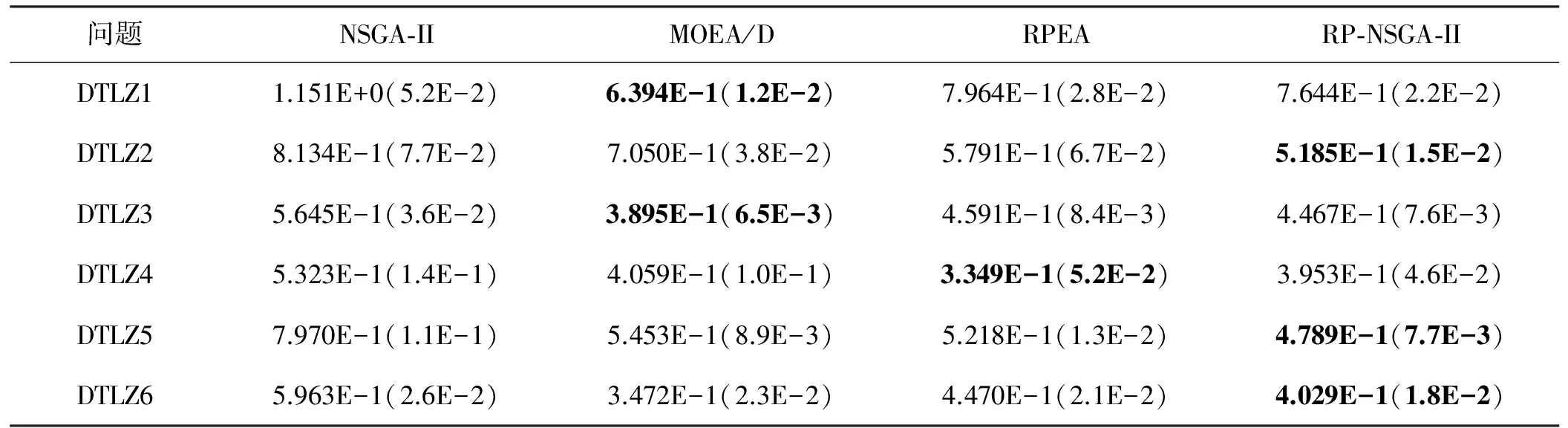
表2 DTLZ测试结果
5 结 语
本文通过对参考点策略的深入研究,对参考点策略提出了改进,并将改进后的参考点策略与NSGA-Ⅱ算法相结合,形成了基于改进参考点的快速非支配排序算法,有效地提高了算法的选择压力。DTLZ函数测试实验表明,RP-NSGA-Ⅱ能够有效地取得更接近Pareto前沿的最优解,适用于解决高维多目标问题。未来的研究方向将集中于两个方面:一是将参考点策略与其他算法相结合,构成在优化高维多目标问题方面具有更好效果的算法;二是将算法应用到实际工程中去。
参考文献:
[1] Wierzbicki A P. The use of reference objectives in multiobjective optimization[M].Springer Berlin Heidelberg: Multiple Criteria Decision Making Theory and Application, 1980:468-486.
[2] Deb K, Sundar J, Chaudhuri S, et al. Reference point based multi-objective optimization using evolutionary algorithms[C]//Conference on Genetic and Evolutionary Computation. New York: ACM, 2006:635-642.
[3] Mohammadi A, Omidvar M N, Li X. Reference point based multi-objective optimization through decomposition[C]//Piscataway, NJ: IEEE, 2012:1-8.
[4] Figueira J R, Liefooghe A, Talbi E G, et al. A parallel multiple reference point approach for multi-objective optimization[J]. European Journal of Operational Research, 2010, 205(2):390-400.
[5] Wang R, Purshouse R C, Fleming P J. Preference-inspired coevolutionary algorithms for many-objective optimization[J]. IEEE Transactions on Evolutionary Computation, 2013, 17(4):474-494.
[6] Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, Part I: Solving problems with box constraints[J]. IEEE Transactions on Evolutionary Computation, 2014, 18(4):577-601.
[7] Zhang Q, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6):712-731.
[8] 孔维健,丁进良,柴天佑.高维多目标进化算法研究综述[J].控制与决策, 2010,25(3):321-326.
[9] Farina M, Amato P. On the optimal solution definition for many-criteria optimization problems[C]//Piscataway, NJ: IEEE, 2002:233-238.
[10] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multi-objective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation,2002, 6(2): 182-197.
[11] Liu Y, Gong D, Sun X, et al. Many-objective evolutionary optimization based on reference points[J]. Applied Soft Computing,2017, 50:344-355.
[12] Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation,2002, 6(2):182-197.
