EET理论在超硬材料相变机理研究中的应用
2018-06-28王功振吕美哲
贾 凤, 王功振, 吕美哲, 许 斌,
(1.山东建筑大学 材料科学与工程学院,山东 济南250101; 2.山东大学 材料科学与工程学院,山东 济南250061)
超硬材料通常是指维氏硬度值超过40 GPa的材料,主要包含金刚石(diamond)和立方氮化硼(cubic boron nitride,cBN)。在此基础上,人们又合成出其他一些超硬材料,如氮化碳、硼碳氮、金属硼化物(WB2、RuB2、OsB2、ReB2)、富硼化物(B4C、B6O)、聚晶材料[1-2]等。当前超硬材料单晶制备方法有:高温高压触媒法、化学气相沉积法、物理气相沉积法、爆炸法、温度梯度法等,综合考虑所制备单晶的强度、韧性、缺陷、晶型等因素,最合适的合成方法为高温高压触媒法[3]。触媒的存在,大大降低了合成的温度压力条件,同时减少了单晶生产成本,也提高了单晶转化率,所以工业上普遍使用高温高压触媒法。目前高温高压触媒法合成的单晶粒度太小以及对金刚石单晶、立方氮化硼单晶的高温高压相变机理不明确,这严重制约了单晶应用范围。几十年来有些学者结合化学、固体物理、晶体学等多学科知识,对金刚石单晶、立方氮化硼单晶的高温高压相变机理给出了一定解释,但都不是很完善;还有些学者基于固体与分子经验电子理论,结合程氏理论,从价电子结构角度合理地分析了金刚石单晶、立方氮化硼单晶的高温高压相变机理[4-9]。

程氏理论(Thomas-Fermi-Dirac-Cheng,TFDC)由程开甲院士提出,该理论认为材料中原子间的边界条件要满足电子密度连续,即量子力学所要求的波函数连续条件[11]。当体系中两晶面间的电子密度差小于10%时,即可确定此组晶面连续,具有诱发相变的可能性。
1 超硬材料单晶相变机理
超硬材料在工业上普遍使用高温高压触媒法合成,由于目前的设备和技术水平很难对高温高压合成块实现原位鉴别和表征,还无法在线检测出高温高压下单晶相变及单晶生长信息,不易对金刚石单晶、立方氮化硼单晶的相变机理给出明确理论。几十年来,研究人员对单晶相变机理提出了一些理论,如固相转变理论、溶剂析出理论、溶剂-催化理论等。
固相转变理论认为在金刚石合成过程中,基于触媒金属的催化作用,石墨中的碳原子不需断键便可直接转变为金刚石结构。触媒金属一般为过渡族金属,在高温高压下,金属触媒一般呈似熔状态,结构上近程有序,其电子轨道中d层未被填满,d层空穴可以吸附碳原子的2pz电子,使碳原子由原来的sp2π杂化状态转变为sp3杂化状态,并促使金刚石结构形成。石墨与金刚石的晶体结构见图1。在立方氮化硼(cubic boron nitride,cBN)合成过程中,六方氮化硼(hexagonal boron nitride,hBN)中的原子无需断键解体,便可在触媒金属的催化作用下,沿hBN轴向方向压缩,当hBN上下两层中的B、N原子压缩到一定距离时,过渡元素原子d层电子空轨道会吸附N原子外层的一个2pz电子,并集中在垂直方向上成键,促使硼、氮原子由sp2π杂化状态转变为sp3杂化状态,从而转变为与金刚石结构相似的cBN,hBN与cBN的晶体结构如图2所示。
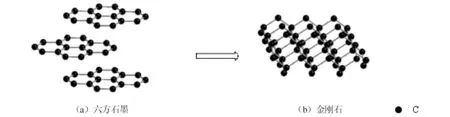
图1 石墨与金刚石的晶体结构图
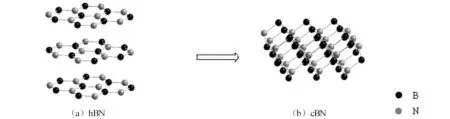
图2 hBN与cBN的晶体结构图
Dideikin A T等研究金刚石单晶的合成机制时,认为在高能爆炸冲击波的作用下,部分石墨直接固相转变为纳米金刚石颗粒(detonation nanodiamonds,DND),然后DND颗粒在烃化物的润滑作用下发生旋转,使得同名晶面间形成很好的晶格匹配,DND颗粒会以定向连生机制(oriented-attachment mechanism)长大[12]。Fukunaga O等在研究cBN单晶的合成机制时(Li3BN2为触媒),发现体系中hBN首先与Li3BN2反应生成亚稳重结晶hBN,之后cBN会在重结晶hBN中形核长大,并从重结晶hBN晶格中沉淀析出[13]。
溶剂析出理论从化学溶体角度来解释许多实验现象,即在该理论中触媒作为溶剂,溶质因溶解度的不同而呈现出溶解或析出的状态。金刚石合成是熔体中石墨溶解金刚石析出的过程;cBN合成过程则是熔体中hBN溶解cBN析出的过程。Shumilova T G等以石墨-碳酸盐体系来研究由亚稳液态碳形成金刚石的机制时,认为在合成条件接近金刚石-石墨平衡线时,形成了含有sp2和sp3杂化碳的亚稳液体,一旦温度压强条件改变,会由液体中的亚稳液态碳析出金刚石晶体[14]。Turkevich V等在研究AlN-hBN中cBN的合成机制时,认为hBN溶解在AlN固溶体中,当BN在AlN中处于过饱和状态时,cBN会从固溶体中析出[15]。
溶剂-催化理论认为在高温高压合成金刚石时,石墨与触媒互相溶解,金刚石一旦成核会在其表面形成一定厚度的金属包膜。碳原子在扩散作用下穿过包膜,并以sp3杂化的金刚石结构从包膜熔体中结晶析出。在该理论框架下,金属触媒兼具溶解和催化两种作用。Guo W等研究Li-B-N系统中的氮化硼相变机制时,发现Li3N首先与hBN发生共熔反应,生成熔融Li3BN2,一旦温度升高到1 460 ℃,cBN将会溶解在Li3BN2中,随着温度的升高,cBN会结晶析出,并认为在cBN的合成过程中,起催化、溶解作用的是Li3BN2而不是Li3N[16]。
总之,各种相变理论具有一定合理性,但也有其局限性,它们可以从一定角度解释部分现象,但不能圆满地解释所有现象。如固相转变理论未能对触媒催化作用与温度的关系、螺旋生长、晶内夹杂物及其分布等问题给出圆满解释;溶剂析出理论忽略了高温高压下所用触媒的状态及结构特征以及各原子及其原子团间的相互作用,对一些能溶解碳却不能形成金刚石的实验现象还无法解释;溶剂-催化理论对触媒状态、结构特征及各原子团间相互作用的解释不足。
2 EET-TFDC理论模型
目前的设备和技术水平很难对高温高压下各种物相进行在线检测,以上理论对于解释金刚石单晶、立方氮化硼单晶的高温高压相变机理仍存在很大争议。许多研究者转换视角,采用基于EET理论构建的EET-TFDC理论模型来研究单晶的高温高压相变机理(见图3),提供了一种从价电子结构角度上分析高温高压下单晶相变机理的方法。
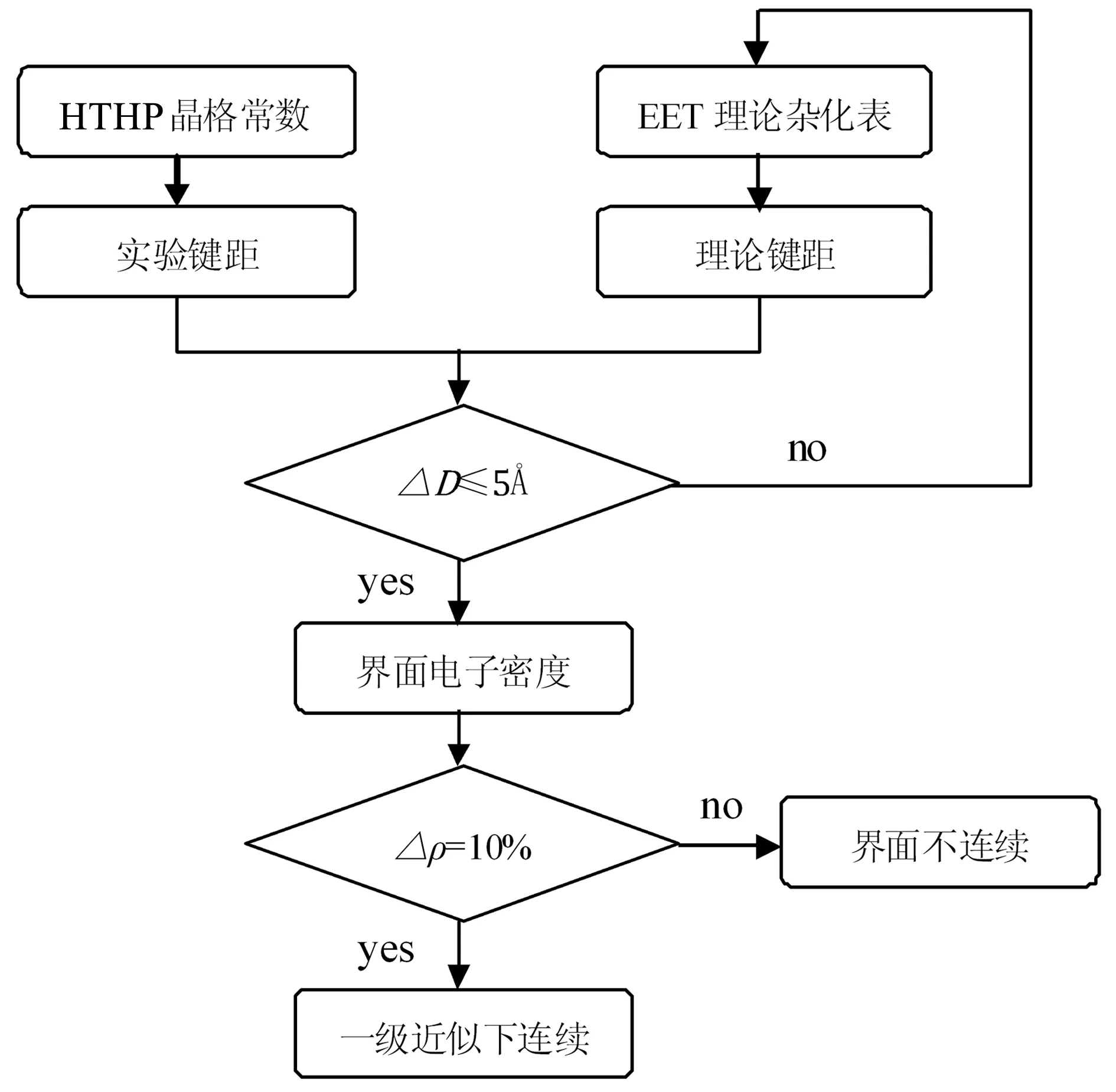
图3 EET-TFDC理论模型框图
3 EET理论在超硬材料合成中的研究现状
近年来,许多学者用EET理论对金刚石单晶、立方氮化硼单晶的合成机理进行了深入研究,并取得了一定进展。文献[4-7]研究发现,在铁镍系触媒合成金刚石的实验中,体系中会形成过渡相Fe3C型碳化物和γ-(Fe,Ni)固溶体,整个触媒中均发现了碳化物(Fe3C)、γ-(Fe,Ni),并且从触媒内层到触媒界面处石墨含量递减,与金刚石直接接触的触媒界面未发现石墨而碳化物(Fe3C)含量却很高,据此推测出金刚石生长所需的碳原子不是来自于石墨而是来自碳化物(Fe3C)的分解,并且金刚石单晶以同质外延生长方式长大。在以Li3N为触媒合成cBN的研究中,文献[8-9]研究发现触媒中均有hBN、cBN、Li3BN2而未检测到Li3N,并且熔体中的hBN、Li3BN2、cBN相均呈近程有序或中程有序状态,在以cBN/触媒界面为基,沿界面垂直向外分层(内层、中间层、外层)取样分析时,发现cBN的含量由内层到外层逐渐减少,据此推测出高温高压下,hBN可以直接转变为cBN,起催化作用的是Li3BN2而不是Li3N。
文献[17-18]利用EET理论,分别对金刚石单晶、立方氮化硼单晶的相变过程进行了研究,并基于EET理论从价电子结构水平上合理解释了单晶的相变过程,相关异相界面间的电子密度差计算结果如表1[17]、表2[17]、表3[17]、表4[18]所示,其中F代表Fe3C ,D代表金刚石,γ代表γ-(Fe,Ni),G代表石墨。
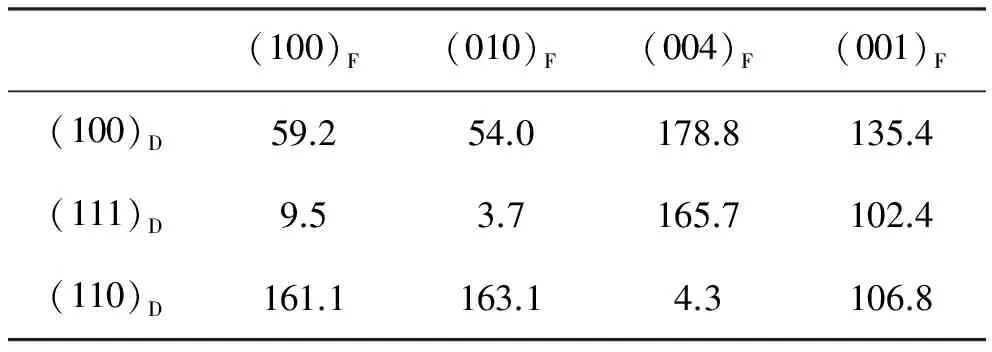
表1 Fe3C/金刚石界面相对电子密度差 %
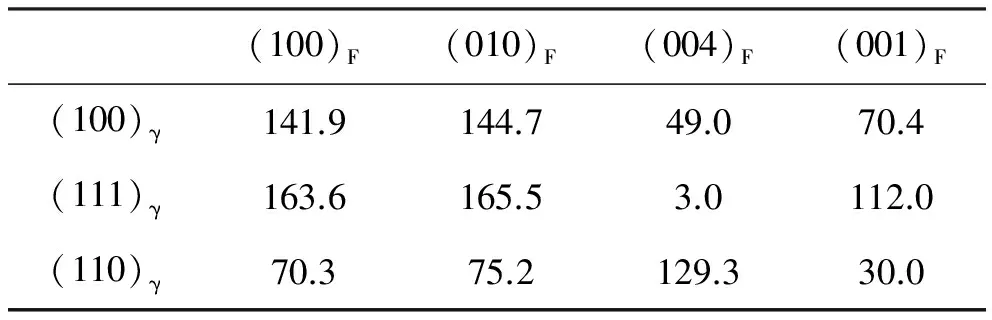
表2 Fe3C/γ-(Fe,Ni)界面相对电子密度差 %
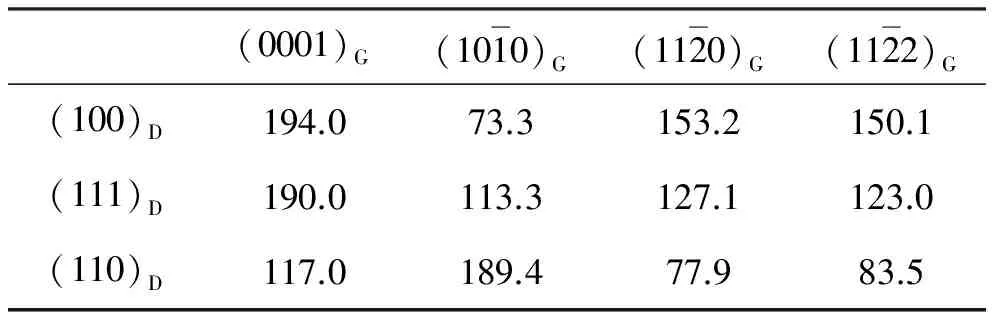
表3 石墨/金刚石界面相对电子密度差 %
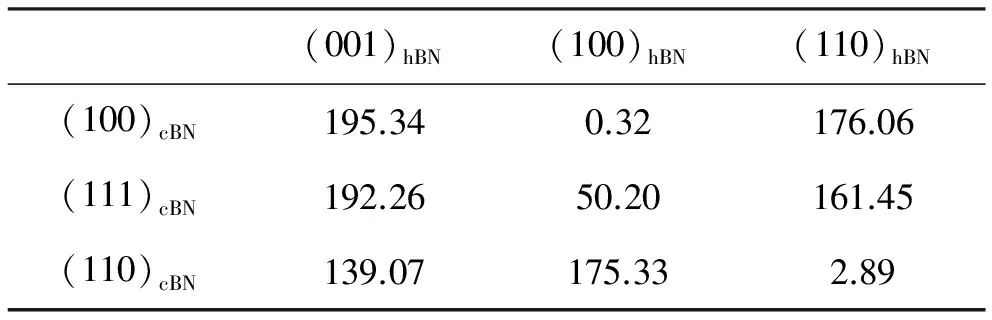
表4 hBN/cBN界面相对电子密度差 %
根据TFDC理论中原子间的边界条件要满足量子力学中电子密度保持连续的要求,如果两异相界面之间电子密度差小于10%,那么就可以认为两异相界面电子密度在一级近似下是连续的。由表1、表2、表3可知,在金刚石单晶合成过程中,Fe3C/金刚石单晶界面出现两组界面电子密度差小于10%,也即有两组Fe3C/金刚石界面电子密度在一级近似下连续。γ-(Fe,Ni)与Fe3C有一组界面电子密度差小于10%,也即γ-(Fe,Ni)/Fe3C有一组界面电子密度在一级近似下连续。石墨/金刚石界面电子密度差很大,远远大于10%,说明石墨/金刚石电子密度在一级近似下不连续,推测出合成金刚石的碳源不可能直接来自石墨,而有可能来自Fe3C的分解,在此过程中γ-(Fe,Ni)主要起催化作用。由表4可知,在cBN合成实验中,hBN/cBN界面有两组电子密度差小于10%,即有两组界面电子密度在一级近似下连续,据此推测出合成cBN的B、N源可能直接来自hBN。
结果分析表明,在静态高温高压触媒法合成金刚石单晶时,主要包含两步:一是碳化物的形成;二是碳化物分解出活性碳原子,为金刚石生长提供碳源。在高温高压下,首先石墨碳原子与触媒反应,生成碳化物与中间相,然后碳化物分解出具有sp3杂化态的活性碳原子,当碳原子在电子结构、能量状态达到金刚石成核条件时,瞬间形核,之后的活性碳原子沉积在金刚石单晶表面,促进单晶长大。基于EET理论推测出的金刚石单晶的相变机理支持溶剂-催化理论,在该相变过程中金刚石单晶的生长碳源来自碳化物分解而不是石墨直接转变,在相变过程中的中间相γ-(Fe,Ni)主要起催化作用。在静态高温高压触媒法合成cBN实验中,首先hBN与触媒反应生成触媒中间相(Li3BN2),在中间相的催化作用下,hBN转变为cBN,在该过程中cBN单晶的B、N源可能直接来自hBN,而中间相(Li3BN2)主要担任催化剂的角色。由EET理论推测出的cBN单晶相变机理支持固相转变理论。
EET理论考虑了材料组成元素的杂化态和晶体结构,将材料的成分、价电子结构和材料性能联系起来。近年来,许多科研人员不断完善和发展EET理论,并广泛应用于计算材料科学领域,由原来对材料物理性能(硬度、耐蚀性能、磁性等)及宏观机械性能等的定性分析阶段,进入到对材料的定量分析阶段。
4 展 望
4.1 EET-TFDC理论模型
EET-TFDC理论模型研究高温高压触媒法合成金刚石单晶、立方氮化硼单晶的相变机理时,即分析碳源相/金刚石、硼氮相/cBN界面的电子密度差是否存在连续性,这种连续性正是单晶生长的边界条件。利用EET理论的计算结果来验证实验[17-18],结果表明用EET理论解释金刚石单晶、立方氮化硼单晶相变机理是可行的。
基于EET理论构建的EET-TFDC理论模型用于超硬材料相变机理的研究,其结果可靠,能够很好地将材料的成分、价电子结构和材料相变联系起来。该理论模型从电子水平上分析了超硬材料的高温高压相变机理,这对其他材料的相变机理研究具有一定借鉴意义,将会更多地应用于关于材料相变机理、磨损断裂机理等方面的研究。
4.2 EET理论与第一性原理
第一性原理是指基于量子力原理,从具体要求出发,经过一些近似处理后直接求解薛定谔方程的方法。用EET理论的计算结果与第一性原理的计算结果来分析金刚石单晶、立方氮化硼单晶的相变机理时,二者得出的结论一致:在金刚石单晶相变过程中,石墨先经中间亚稳相,再由亚稳相释放出sp3杂化碳原子[17,19-21];在cBN单晶相变过程中,hBN的(100)晶面与cBN的(100)晶面的晶面能、晶面价电子密度均连续,可以诱发相变[18,22]。相比而言,第一性原理需要对薛定谔方程进行多次近似处理,计算过程繁琐,尤其在多元合金的计算方面,第一性原理不尽完美而EET理论却显示出了独特的优势。当然,EET理论[23]也存在诸多不足之处,比如计算值过度依赖实验值、计算精度过低、该领域研究人员比较少、国内研究者参与度不高、国际认知度较低等。面对诸多不足,需要广大研究人员共同努力,可以将EET理论与其他电子理论有机结合起来,不断完善和发展EET理论,使EET理论在计算材料学领域发挥越来越重要的作用。
4.3 电子理论与新材料成分设计
对材料领域诸多问题的研究,有必要深入到电子层次,而EET理论为其提供了一种简便、高效、快速的电子水平分析方法。近年来,EET理论不断完善和发展,先后经历了定性探讨、定量设计两个阶段。EET理论已经成功应用在金属及其合金、陶瓷材料等领域,研究内容包括材料相变机理、物理性能(硬度、耐蚀性能、磁性等)及宏观机械性能、合金元素作用、组织形态等;此外,在钛合金[24-25]、不锈钢[26]、低合金高强度钢[27]等合金成分定量设计方面也取得了一定成果。相信经过广大科研人员的共同努力,EET理论将会更好地应用于材料性能改善、新材料发展等领域,更好地指导工业生产。
参考文献:
[1] Lu J, Kou Z, Liu T, et al. Submicron binderless polycrystalline diamond sintering under ultra-high pressure[J]. Diamond & Related Materials, 2017, 77:41-45.
[2] Zhang Z, Huang S, Chen L, et al. Ultrahigh hardness on a face-centered cubic metal[J]. Applied Surface Science, 2017, 416:891-900.
[3] Xu C, He D W, Wang H K, et al. Synthesis of novel superhard materials under ultrahigh pressure[J]. Chinese Science Bulletin, 2014, 59(36): 5251-5257.
[4] Yin L W, Li M S, Cui J J, et al. Diamond formation using Fe3C as a carbon source at high temperature and high pressure[J]. Journal of Crystal Growth, 2002, 234(1):1-4.
[5] 许斌,宫建红,李木森,等.铁基金属包膜内Fe3C的行为与高温高压金刚石单晶转变[J].金属学报,2005,41(10):1101-1105.
[6] Xu B, Li L, Li M S, et al. The carbon source analysis for diamond crystal growth from Fe-C system at high pressure-high temperature[J]. Advanced Materials Research, 2008, 51(51):141-147.
[7] Xu B, Yang H M, Guo X F, et al. Research progress on the correlation between catalyst and cubic boron nitride synthesis under static HPHT[J]. Journal of Synthetic Crystals, 2012, 41: 137-142.
[8] Guo X F, Xu B, Zhang W, et al. XPS analysis for cubic boron nitride crystal synthesized under high pressure and high temperature using Li3N as catalysis[J]. Applied Surface Science, 2014, 321(321): 94-97.
[9] Xu B, Yang H M, Guo X F, et al. Research progress on the correlation between catalyst and cubic boron nitride synthesis under static HPHT[J]. Journal of Synthetic Crystals, 2012, 41: 137-142.
[10] 余瑞璜.固体与分子经验电子理论[J].科学通报,1978,23(4):217-224.
[11] 程开甲,程漱玉.TFD模型和余氏理论对材料设计的应用[J].自然科学进展:国家重点实验室通讯,1993(5):417-432.
[12] Dideikin A T, Eidelman E D, Kidalov S V, et al. Oriented-attachment growth of diamond single crystal from detonation nanodiamonds[J]. Diamond & Related Materials, 2017, 75:85-90.
[13] Fukunaga O, Takeuchi S. Growth mechanism of cubic BN using Li3BN2solvent under high pressure[J]. International Journal of Refractory Metals & Hard Materials, 2016, 55:54-57.
[14] Shumilova T G, Isaenko S I, Tkachev S N. Diamond formation through metastable liquid carbon[J]. Diamond & Related Materials, 2016, 62:42-48.
[15] Turkevich V, Taniguchi T, Andreev A, et al. Kinetics and mechanism of cubic boron nitride formation in the AlN-BN system at 6 GPa[J]. Diamond & Related Materials, 2004, 13(1):64-68.
[16] Guo W, Shi Y, Yang P, et al. Characterization of boron nitride phase transformations in the Li-B-N system under high pressure and high temperature[J]. Journal of Alloys & Compounds, 2015, 644:888-892.
[17] 许斌,范小红.触媒法金刚石单晶合成的高温高压相变机理[M].北京:科学出版社,2014:192-195.
[18] 许斌,吕美哲,张文,等.高温高压下cBN单晶转变机理的EET理论分析[J].人工晶体学报,2015,44(10):2714-2720.
[19] 阴知见. sp3键合的金刚石与氮化硼多型第一性原理研究[D].秦皇岛:燕山大学, 2013.
[20] Wang J T. Energetics and kinetics of direct phase conversion from graphite to diamond[J]. Science China (Physics Mechanics & Astronomy), 2013, 56(12):2266-2271.
[21] Wang L, Wan Q, Hu W, et al. The local states density and band structure of diamond and graphite studied by first principles molecular dynamics[J]. Computers & Applied Chemistry, 2010, 27(6):735-738.
[22] 时永鹏.基于研究cBN单晶转变的晶面能计算及晶面形貌表征[D].济南:山东建筑大学,2017.
[23] 林成,黄士星,尹桂丽,等.固体与分子经验电子理论的发展现状与展望[J].兵器材料科学与工程,2016,39(1):110-114.
[24] 赵永庆,曾卫东,林成,等.钛合金的定量研究进展[J].中国材料进展,2014,33(9-10):535-544.
[25] 赵永庆,曾卫东,林成.钛合金数据库系统的开发、显微组织定量表征及亚稳β钛合金的成分理论设计研究[J].中国材料进展,2009,28(6):51-55.
[26] 李春福,童丽华,程定春,等.不锈钢耐蚀性能的价电子理论研究进展[J].钢铁,2015,50(1):1-4.
[27] 俞杰.EET理论在低合金高强度钢成分设计中的应用[J].现代冶金,2017,45(4):13-17.
