一种基于激光超声的薄层金属材料厚度检测方法研究

刘永强， 杨世锡， 甘春标

(浙江大学 机械工程学院 流体动力与机电系统国家重点实验室，杭州 310027)

随着材料工程的发展，综合性能优良的薄层金属材料被广泛用于航空航天、汽车制造及生物医学等领域，在各类工程技术中占有越来越重要的地位。如薄层蒙皮是航天飞行器的重要承力构件，主要承受横向气动力并将其转换成机翼的弯矩和扭矩，是航天飞行器关键部件之一[1-2]。蒙皮厚度直接影响机翼动力学特性，拉伸后蒙皮厚度不均匀，会使机翼局部应力过大而导致结构失效，甚至造成机毁人亡的严重后果。对飞行器蒙皮厚度进行无损检测是实际生产过程中必不可缺的一个环节。

蒙皮等薄层金属材料厚度的无损检测方法主要有超声检测、涡流检测以及红外热成像检测等[3-5]。其中，超声检测因系统成本低、便于携带、检测精度相对较高等特点被广泛使用。根据工作原理不同，超声检测方法主要分为共振法[6-7]、兰姆波法[8]和脉冲反射法。脉冲反射法原理简单，对材料表面光滑度要求低，是目前发展最完善、应用最广泛的测厚方法。然而脉冲反射法所用传统超声波频率低(一般小于20 MHz)、波长长，对薄层金属材料厚度进行检测时，相邻反射信号易混叠；同时压电传感器必须通过耦合剂与被测试件黏接，耦合剂不仅可能对试件造成污染，还会增大测量间隙引起测量误差。因此传统超声检测法测厚下限一般为1 mm，无法满足实际工程需求[9]。激光超声检测，即利用激光辐照材料表面，在材料内部产生超声波进行厚度检测，其激发声波频率高(一般可高达100 MHz)、波长短，声波的激发与接收都可通过激光束完成[10-12]，能实现薄层材料厚度的非接触式检测，且检测精度高、速度快，可取代传统超声检测法对薄层材料厚度进行检测。

论文主要提出一种基于激光超声的薄层金属材料厚度检测方法以解决薄层材料的厚度检测问题。①对激光辐照后材料内波动方程进行求解，提出一种材料厚度计算方法，给出材料厚度计算公式；②提出一种激光超声回波信号特征量提取方法，能准确获取激光超声在材料内的传播时间，有效保证了材料厚度的检测精度；③通过搭建试验系统对不同厚度铝合金试样块进行检测，验证了所提测厚方法的可靠性；最后对全文内容进行总结。

1 激光超声测厚基本原理

激光辐照在材料上表面一点时，入射激光能量通过逆韧致过程在材料表面趋肤深度内被部分吸收，并在亚纳秒时间内转化为热能。激光加热使材料局部升温，发生热膨胀、产生热应力，进而在材料表面及内部激发出超声波，主要包括沿材料上表面传播的表面波及在材料内部传播的体波。关注材料下表面一对心点，在一定时间范围内，该点处只能接收到体波。激光与材料相互作用示意图，如图1所示。从图1可知，A为材料上表面受激光辐照点，B为材料下表面对心点，B点是过材料上表面受激光辐照点做上表面垂线，垂线与下表面的交点。

1.1 对心点位移计算

激光辐照材料上表面A点后，因体波作用，对心点B会上下振动。假设入射激光能量密度Q(x,t)具有如下表示形式

Q(x,t)=I·N(x)·q(t)

(1)

式中：I为入射激光峰值能量密度大小；N(x)，q(t)分别为I在空间、时间上分布的归一化函数。

图1 激光辐照材料表面示意图Fig.1 Schematic of laser irradiating at material

由Rose[13]的研究成果知，此时材料内部位移场分布u(x,t)可以表示为

(2)

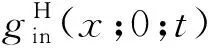
(3)

此时，质点运动方程也可以利用Helmholtz势表示为[14]

(4)

(5)

f1=Aσ(x)σ(y)σ(z)H(t)

(6)

f2=Bσ(x)σ(y)σ(z)H(t)

(7)

式中：ρ,α与β分别为材料密度、激光所激发出的纵波与横波在材料内的传播速度;f1与f2为激光束在材料表面引起的等效热应力值;A,B为常数，分别表征引起纵波与横波热应力力源幅值大小;σ为狄拉克函数；H(t)为阶跃时间函数。

对式(4)、式(5)取双重Fourier-Laplace变换，再通过Cagniard-De Hoop反演法[15]，可以得到位移势表达式如式(8)、式(9)所示

(8)

(9)

为得到声波到达对心点B的相对时间，可将激光束在时间上的分布函数q(t)取为δ(t)函数以简化计算，式(2)变为

u(x,t)=EaTkI[(1-2υ)K]-1·gH(x;0;t)

(10)

将式(8)、式(9)代入式(10)，可得到入射纵波、横波引起的位移值分别为

(11)

(12)

式(11)、式(12)中Z为板材厚度。利用Matlab画出对心点B处的位移波形图，如图2所示。

根据式(11)、式(12)计算结果可知，图2中在时间轴tp及ts处出现的波形分别为纵波与横波；若不考虑波传播损耗情况，在时间轴tp及ts处到达对心点B的纵波与横波经过反射回到材料上表面A点，在上表面A点反射后再次回到B点时将以同图2中完全相同的形式周期出现。

图2 对心点B位移波形图，泊松比ν=1/3Fig.2 Displacement of position B, for poison ratio ν=1/3

由式(8)、式(9)可得，纵波到达B点的时间tp、横波到达B点的时间ts可以表示为

(13)

(14)

由式(13)、式(14)知，相邻两纵波或相邻两横波之间时间间隔是对应声波传播过两个材料厚度Z所用时间。

1.2 厚度检测基本原理

1.2.1 激光超声测厚方法

对式(13)、式(14)所得结果进行推论，有

(15)

或

(16)

式中： Δtp与Δts分别为相邻两纵/横波到达对心点B的时间差值。在固体材料中，纵波传播速度远大于横波传播速度，当所记录波形到达次数N相等时，纵波用时更少，这有利于提高厚度检测效率。因此采用式(15)作为材料厚度计算公式。为使计算结果更为精确，取多次相邻纵波到达时间差的平均值进行计算。假设纵波第N次到达材料底面对心点B的时间为tpN，则材料厚度可以表示为

(17)

式中： Δtp(N-1)=tpN-tp(N-1)。若纵波在材料中的传播速度α已知，测得相邻各纵波到达材料底面对心点B处的时间差，就可根据式(17)计算材料厚度Z。实际上因材料种类众多、内部结构各异，声波在其内部传播的声速等特性可能是未知的，为提高材料厚度检测精度，宜通过试验测得激光超声纵波在待测材料内的实际传播速度，进而利用式(17)求得材料厚度。下面简要介绍激光超声纵波传播速度测量基本原理。

1.2.2 激光超声纵波波速测量方法

由式(15)可知，当材料厚度Z已知时，激光超声纵波在材料中的传播速度可以通过式(18)进行计算

(18)

为使计算结果更为精确，取多个相邻纵波到达材料底面对心点B处时间差的平均值进行计算。假设纵波第N次到达底面对心点处的时间为tpN，则纵波在材料内的传播速度就可以表示为

(19)

式中： Δtp(N-1)=tpN-tp(N-1)。当样品材料厚度Z已知，可以测得相邻各纵波到达材料底面对心点B处的时间差，根据式(19)能计算出纵波在该材料中的传播速度。

2 试验系统

2.1 激光超声测厚系统

试验使用的激光超声厚度检测系统包括激光发射装置及超声检测装置。激光脉冲由Nd:YAG激光发射器激发，波长1 064 nm，脉冲宽度10 ns，发射激光束最大能量为10 mJ，经凸透镜聚焦后激光光斑直径为0.3 mm，垂直入射到2024铝合金试样块上表面。在试样块底面对心点处安置纵波传感器接收激光超声纵波。所用纵波传感器为奥林巴斯高频传感器(V375-SU)，直径6 mm，中心频率为30 MHz。传感器采集到的位移信号经前置放大器放大后传送给高速数据采集卡，放大器放大倍数为40 dB，高速数据采集卡采样频率为100 MHz。采集到的数据存储在上位机中，供后续分析使用。试验系统如图3所示。

2.2 试验试样

试验使用试样均为长方体2024铝合金块，长宽高分别为150 mm×50 mm×Zmm。超声速度检测试验中所用铝合金块高度分别为4 mm±5 μm与8 mm±5 μm。厚度检测试验中待测铝合金试样块厚度在0.2～20 mm内变化。待检测试样块各项参数值，如表1所示[16]。

表1 试样块热力学参数表

1-激光发射器；2-扫描振镜；3-数据采集系统集成； 4-待检测试样；5-压电传感器；6-三维移动平台； 7-数据处理系统图3 激光超声测厚系统Fig.3 Schematic diagram of laser testing system

3 试验结果及讨论

3.1 激光超声纵波速度检测

3.1.1 速度检测试验结果及分析

激光超声纵波传播速度检测试验中，传感器测得4 mm±5 μm， 8 mm±5 μm厚试样块对心点处位移波形图，如图4、图5所示。所得试验数据已经过64次的叠加平均处理以提高信噪比。

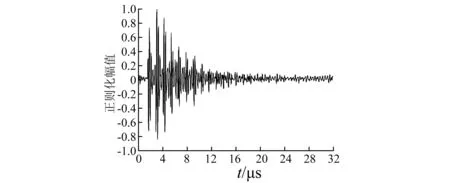
图4 4 mm±5 μm厚试样块对心波形图Fig.4 Longitudinal waves in 4 mm±5 μm alloy

观察图4及图5所得位移波形图，可以发现图中都包含一系列等时间间隔峰值点，由式(13)知，相邻两波峰间的时间间隔是激光超声纵波在试样块中传播一个来回所用时间；从图中可知，各峰值点的幅值在不断减小，这是材料阻尼等作用引起超声纵波能量衰减的结果；从图中还能看出相邻两峰值信号之间存在一些幅值较小的波形信号(见图5中箭头所指信号)，这些信号经过多次叠加平均也没有消失。根据信号出现时间推论，这是横波在试样块边界处发生波形转换变为纵波而被传感器接收的。理论上，在激光辐照点与对心点处不会有波形转换发生，实际因传感器晶片有一

定尺寸大小，并不能完全简化为一个点，因此在对心点处会有部分模式转换波被传感器接收，从而出现了图5中箭头所指信号。进一步观察图4、图5中的各峰值信号可发现，各峰值信号的结构组成是比较复杂的，每个时间点处对应的峰值信号都是由多个尖峰组成。这是由传感器自身特性决定的。想要获得准确的超声速度值，首先要获取各波峰到达对心点B的准确时间值，就需要对图4、图5中的位移波形图进行信号处理以获取准确、唯一的波峰到达时间值。

图5 8 mm±5 μm厚试样块对心波形图Fig.5 Longitudinal waves in 8 mm±5 μm alloy

3.1.2 时域波形信号峰值提取

论文对时域波形信号进行处理的基本流程是：①对激光超声时域信号进行降噪处理，最大限度的去除信号中夹杂的低幅值、高频率背景噪声；②对获得的有效信号值求解上包络线；③对得到的包络线进行平滑处理，进一步去除小幅值背景噪声。以得到峰值信号到达所对应的准确、唯一时间值。

使用经验模态分解法(Empirical Mode Decomposition, EMD)[17-18]对信号进行降噪处理。从图4、图5试验检测结果可知，实际接收的超声信号是一种时变非平稳信号，而EMD对时变非平稳信号具有较强的分析能力；其次，试验前可以预估待检测试样块厚度范围，进而可对有效信号值的出现时间进行预判，令信号记录时间大于预判值，可以有效避免EMD在数据拟合过程中出现的过冲/欠冲及端点问题；基于同样的原因，采用Hilbert变换求解降噪后信号的上包络值，以将结构复杂的峰值信号转化为结构单一、峰值凸出的波形信号；最后再对上包络信号进行平滑处理，去除小幅值转换波形信号及背景噪声，就可获取峰值信号到达得准确、唯一时间值。利用Matlab编写对应程序对图4、图5中数据进行处理，处理过程及结果，如图6、图7所示。

图6 4 mm铝合金板数据处理过程图Fig.6 Schematic of data processing for 4 mm plate

图7 8 mm铝合金板数据处理过程图Fig.7 Schematic of data processing for 8 mm plate

对比图4、图5与图6(d)、图7(d)可知，原波峰混叠、背景噪声复杂、结构复杂的双极性对心波形信号经过数据处理后变为单一峰值的单极性信号，从图6(d)与图7(d)中可以准确读出各次波峰到达时间值。

3.1.3 纵波传播速度计算

从图6(d)、图7(d)中读取各峰值信号到达时间值，进而利用式(19)计算激光超声纵波在2024铝合金试样块中的传播速度，结果如表2所示。

对比计算结果可知，激光超声纵波在本次试验使用的2024铝合金试样块中的传播速度约为6 482 m/s；这与文献[19]给出的纵波传播速度比较接近，说明此次激光超声纵波传播速度检测试验结果是可靠的，同时表明论文使用的数据处理方法是准确的。后续试验将6 482 m/s视为激光超声纵波在2024铝合金试样块中的传播速度。

3.2 试样块厚度检测

3.2.1 试样块厚度检测试验结果

利用所搭建激光超声测厚系统对0.2～20 mm厚铝合金试样块厚度进行检测。利用“3.1”节中引入的时域信号处理方法对试验结果进行处理，以得到各峰值信号到达的准确时间值，再根据式(17)计算材料厚度，所得结果如表3所示。

表3给出了铝合金试样块厚度的实际值、检测值及检测的相对误差。所有检测值都是将试样块厚度检测3次，取3次检测结果计算平均值得到。根据计算结果利用指数函数拟合法得到厚度检测相对误差与试样厚度值得关系曲线图，如图8所示。表2及表3中时间值均通过处理后信号波峰值提取得到。

表2 激光超声纵波传播速度计算结果

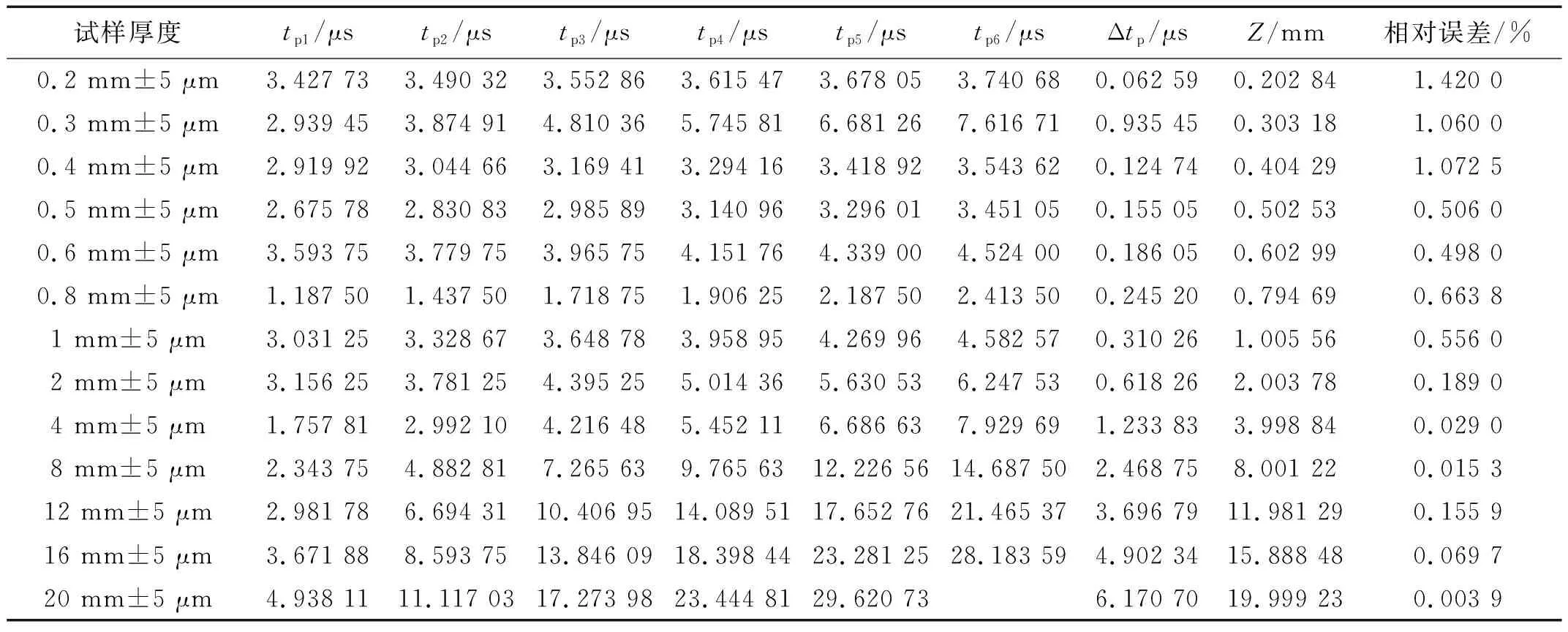
表3 试样块厚度实际值与检测值

3.2.2 试验结果分析

从表3及图8可知，检测值与真实值基本相符；当待检测样块厚度在0.2～0.5 mm时候，测厚系统检测的相对误差在1%～1.42%波动，当待检测样块厚度大

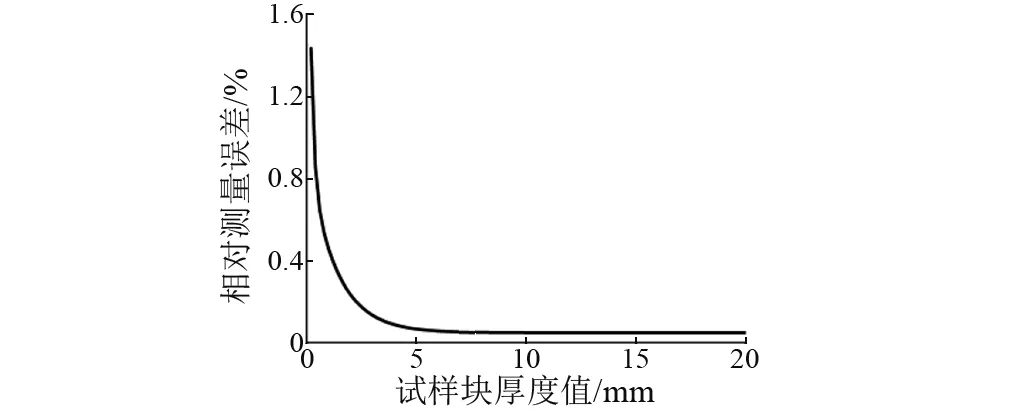
图8 相对测量误差与试样厚度关系曲线图Fig.8 Relative error as a function of measuring thickness

于0.5 mm时，测厚系统检测的相对误差保持<0.67%，随着试样块厚度增加，厚度检测的相对误差在不断减小，厚度计算结果更为准确。出现这种现象的原因是当试样块厚度增加时，激光超声纵波在试样块内部传播的时间增大，不易出现波峰混叠现象，时域信号处理简单，因而材料厚度越大检测结果将越精确。所搭建激光超声测厚系统厚度检测最小值可到0.2 mm，其测厚范围超过传统超声波测厚系统。试验结果验证了所提测厚方法的可行性。

所述基于激光超声的材料厚度检测方法，其厚度检测下限值主要受纵波传感器性能及时域信号处理方法限制。选用敏感度更高的激光干涉仪，所测超声波峰值信号结构简单、相邻波峰间隔更明显，所述信号处理方法计算结果将更精确，测厚下限值将进一步得到提升。测厚方法上限值主要受波能量值及其衰减速度限制，激光束所激发超声波能量越大、声波传播衰减越小，测厚上限值将进一步得到提升。因此在不损伤材料的前提下，提高激光束能量密度、使用阵列光源等均可提高检测厚度范围。

4 结 论

提出一种基于激光超声的薄金属材料厚度检测方法，该方法能够克服传统超声脉冲回波法难以检测薄层材料厚度的缺点，厚度检测精度高、速度快。通过建立、求解激光辐照后材料内波动方程，得到材料底面对心点处位移波形图，阐述了所提测厚方法基本原理、给出了厚度计算表达式；提出一种激光超声回波信号特征量提取方法，能准确获取激光超声在材料内传播时间值，保证了厚度检测精度；搭建试验系统对不同厚度2024铝合金试样块厚度进行检测，试验结果表明，相对传统超声波测厚方法，所提基于激光超声的测厚方法测量结果更可靠性、更准确。提高传感器中心频率值、提高激发超声波能量束密度、使用阵列光源等还可进一步提高本测量方法测量范围与测量精度。本方法还可进一步用来检测超声传播速度及材料的衰减系数。

参 考 文 献

[ 1 ] GUO Xijuan, ZHAO Qiang, XI Fengfeng. Design segmented stiff skin for a morphing wing[J]. Journal of Aircarft, 2016,53(4): 962-970.

[ 2 ] SKULBORSTAD A J, SWARTZ S M, GOULBOURNE N C. Biaxial mechanical characterization of bat wing skin[J]. Bioinspiration & Biomimetics, 2015,10(3): 1-16.

[ 3 ] 肖锋,华宏星,谌勇,等.潜艇湿表面抗冲覆盖层压缩特性及抗冲击性能研究[J].振动与冲击,2013,32(18): 126-132.

XIAO Feng, HUA Hongxing, CHEN Yong, et al. Compression and shock resistance performance of an anti-shock layer coated on wet surface of submarine[J]. Journal of Vibration and Shock, 2013,32(18): 126-132.

[ 4 ] 邵泽波,刘兴德.无损检测[M].北京:化学工业出版社,2011.

[ 5 ] 唐力伟,张晓涛,王平.管状金属构件裂纹电磁声发射激发特性试验研究[J].振动与冲击,2014,33(19): 48-58.

TANG Liwei, ZHANG Xiaotao, WANG Ping. Tests for exciting features of electromagnetic acoustic emission of tubular metal parts’ crack[J]. Journal of Vibration and Shock, 2014,33(19): 48-58.

[ 6 ] 李家伟.无损检测手册[M].北京:机械工业出版社,2012.

[ 7 ] DIXON S, EDWARDS C, PALMER S B. High accuracy non-contact ultrasnic thickness gauging of aluminium sheet using electromagnetic acoustic transducers [J]. Ultrasonics, 2001,39(6): 445-453.

[ 8 ] LATYSHEV A V, YUSHKANOV A A. Nanofilm thickness measurement by resonant frequencies [J]. Quantum Electronics, 2015,45(3): 270-274.

[ 9 ] LUO W, ROSE J L. Lamb wave thickness measurement potential with angle beam and normal beam excitation[J]. Materials Evaluation, 2004,62(8): 860-866.

[10] AMZIANE A, AMARI M, MOUNIER D, et al. Laser ultrasonics detection of an embedded crack in a composite spherical particle [J]. Ultrasonics, 2012,52(1): 39-46.

[11] MONCHALIN J P, AUSSEL J D. Ultrasonic velocity and attenuation determination by laser ultrasonics[J]. Journal of Non-destructive Evaluation, 1990,9(4): 211-221.

[12] 丁一珊，杨世锡，甘春标. 利用激光超声技术研究金属裂纹缺陷的检测波特性[J].振动与冲击,2015,34(14): 33-37.

DING Yishan, YANG Shixi, GAN Chunbiao. Detecting features of defect metal based on laser ultrasonic technique[J]. Journal of Vibration and Shock, 2015,34(14): 33-37.

[13] ROSE L R. Point-source representation for laser-generated ultrasound[J]. Journal of The Acoustical Society of America, 1983,75(3): 723-732.

[14] KEIITI A K, RICHARDS G. Quantitative seismology[M]. San Francisco: University Science Books, 1980.

[15] DEHOOP A, VANDERHIJDEN G. Generation of acoustic-waves by an impulsive line source in a fluid solid configuration with a plane boundary[J]. Journal of The Acoustical Society of America, 1983,74(1): 333-342.

[16] 吴宗泽.机械设计师手册[M].2版.北京：机械工业出版社,2008.

[17] FLANDRIN P, RILLING G, GONCALVES P. Empirical mode decomposition as a filter bank[J]. IEEE Signal Processing Letters, 1999,21(3): 285-288.

[18] WU Z H, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceedings of The Royal Society A-Mathematical Physical and Engineering Sciences, 2004,460: 1597-1611.

[19] LABY H T. Tables of physical and chemical constants [M]. Cleveland: World Publishing Company, 1999.