地震动作用下三层框架模型倒塌的平行双目视觉监测

单宝华， 王 海， 袁文厅， 左占宣， 李 爽

(1.哈尔滨工业大学 土木工程学院，哈尔滨 150090; 2.哈尔滨工业大学 结构工程灾变与控制教育部重点实验室，哈尔滨 150090)

近年来，世界范围内发生多次破坏性地震，造成极大的经济损失及人员伤亡，因此对结构的抗震性能研究显得尤为重要[1]。将地震波输入到结构模型并测量结构模型的振动反应是一种较好的研究结构抗震性能的方法。目前，测量结构振动反应的方法主要包括两种，即接触式测量法和非接触式测量法。

工程上用于结构位移和加速度测量的接触式测量仪器主要有位移传感器、引伸计、加速度传感器等，上述方法均需提前在被测对象表面布设传感器，准备工作复杂。而实际工程中，对于许多动态测量问题，结构的失效和破坏过程是研究者最关心的。但当接触式传感器本身也随着测量对象的失效破坏而损坏时，就会导致动态测量的失败，无法获得结构倒塌过程的全程变形曲线。

常用于振动变形测量的非接触式测量方法有激光位移传感器、GPS和视觉测量法等[2]。激光位移传感器测量精度高，但每次只测量一点，只能得到一个方向位移信息。GPS在实际工程中有广泛应用，同激光位移计一样只对一个测点进行测量，还存在转场的问题。且这两种方法的测量仪器价格均比较昂贵。传统视觉测量中的单摄像机数字图像相关法可同时进行多点面内位移测量，但无法满足面外位移测量要求, 且使用时要求相机必须尽量垂直于被测对象表面。而立体视觉技术通过分析两相机采集到的图像建立被测对象的三维信息，可以测量结构的面内、面外位移及应变。立体视觉方法作为一种精度高、非接触、全场三维多点实时测量技术[3]，越来越受到人们的重视，目前已成为土木工程领域中测量结构振动变形的有力工具[4]。但立体视觉方法的测量误差与物距平方成反比，使用中应尽量将物距控制在数百厘米至数米的量级[5]。因此，将该方法用于实验室模型测量是可行的，但是对于实际结构全程动态测量，使用中会受到物距的制约。

自20世纪以来，国内外许多学者利用立体视觉方法对结构在动荷载作用下振动变形信息进行测量。Chang等[6]采用利用双目视觉测量技术对地震荷载作用下的框架模型进行动态试验测量。Mcginnis等[7]利用数字图像相关方法，对一个6层框架模型基底输入地震动(在地震动输入方向仅有一排柱子)试验进行测量，获得每层位移曲线，获得构件的变形和框架梁柱节点处的转动数据，为该模型的分析提供了详细的变形信息。Shan等[8]使用立体视觉方法完成桥梁拉索模型自由振动监测试验，测得桥梁拉索模型三维位移时程曲线，测量精度较高。

综上所述，虽然上述立体视觉方法可获得不同加速度峰值地震波作用下结构模型的位移时程曲线，但没有用于结构模型倒塌的全程监测。本文将立体视觉方法与数字图像相关方法结合起来监测地震波作用下三层框架模型的倒塌过程，获得三层框架模型倒塌全程位移曲线，以验证该方法用于结构大变形全程动态测量的可行性。

1 立体视觉三维测量原理

本文以平行双目视觉模型为基础进行三维变形测量，平行双目视觉是最简单的双目立体视觉模型，用该模型进行三维坐标测量是基于视差原理[9]，如图1所示。假设两摄像机的成像平面在同一平面内，两摄像机同时观察空间同一物点P，分别得到左右摄像机相互独立的图像坐标为Pl(Xl,Yl)及Pr(Xr,Yr)。因为两摄像机的成像平面共面，故Yl=Yr=Y。设物点P在左摄像机坐标系中的坐标为P(xc,yc,zc)，则视差为Disparity=Xl-Yr。因此，计算点P在左摄像机坐标系下的坐标为

(1)

式中：基距B、焦距f可通过摄像机标定获得，本文采用基于2D共面参照物方法标定得到[10]。

由式(1)可知，当给定基距B、焦距f时，已知空间点在左右图像中的视差Disparity，就可求出该点三维空间坐标。本文经过比较分析，选择Geiger等[11]提出的大范围有效匹配算法(Efficient Large-scale Stereo, ELAS)计算视差。该方法是一种基于特征的图像匹配算法，可对视差进行有效的插值，能够获得高像素图像的致密视差图。

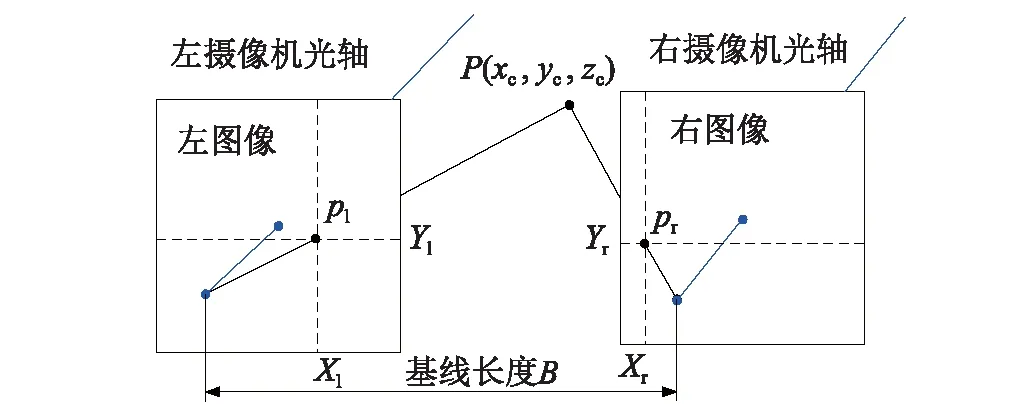
图1 平行双目视觉模型Fig.1 Parallel binocular model

ELAS算法具体计算视差过程如下：①寻求能够准确匹配的点，也称之为支持点集；以此为基础，结合三角剖分方法插值，求参考图(左图像)中观测点的先验概率；②利用左图与右图的灰度相关性，求表征左、右图像相似性的似然概率；③在上面步骤中获得的支持点集和左图观测点的条件下获得右图采样，使用最大后验概率(Maximum A Postiriori, MAP)得到视差计算模型；④对MAP做简单变换，生成能量函数，并且使之达到最小值，此时得到的视差即为所求。

2 空间三维位移计算

结构三维变形是通过结构测点的三维坐标计算获得。由上可知，本文选择基于特征的ELAS计算测点三维坐标, 用于同一时刻左、右图像的立体匹配；而对于左、右相机的时序图像匹配，经比较分析，本文选择基于区域匹配的数字图像相关法(Digital Image Correlation, DIC)方法来实现[12]。

2.1 DIC

DIC通过处理变形前后被测物体表面图像来获得位移和应变信息，其原理如图2所示。数字DIC进行

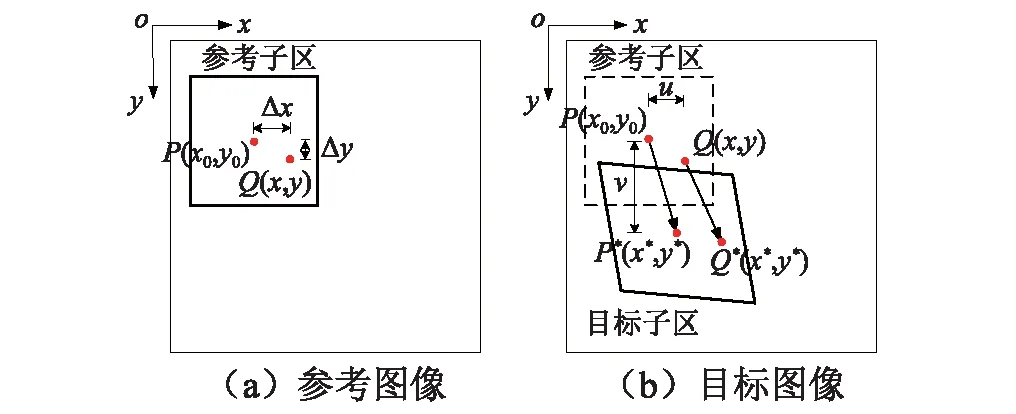
图2 数字图像相关法原理图Fig.2 Sketch map of DIC

整像素相关搜索，首先选定测点Q(x,y)附近整像素点P(x0,y0)，并以点P为中心建立一个(2M+1)×(2M+1)参考子区；然后以此作为匹配模板，在目标图像中按照某一相关函数进行计算，寻找与参考子区相关系数最大、以P*(x*,y*)为中心的目标子区，以确定参考子区中心点P位移初值(u,v)。

经过上述搜索得的只是整像素值，而实际位移值往往是非整像素的。为进行亚像素搜索，本文选取一阶位移模式对图像灰度进行插值。如图2所示，点P为参考子区中心，Q为测点，且P*,Q*为变形后目标子区对应于P,Q的两点，则点Q*坐标见式(2)

(2)

式中：Δx，Δy为点Q(x,y)到子区中心P(x0,y0)的距离；u,v为参考子区中心在x,y方向上的位移；ux,uy,vx,vy为参考子区位移梯度。

本文使用DIC处理不同时序被测物体表面图像，选择式(3)所示的零均值归一化互相关函数(Zero-normalized Cross-Correlation, ZNCC)[13]进行相关计算。该相关函数考虑光照不均匀分布，具有较强的抗干扰能力。

CZNCC(p)=

(3)

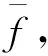
本文使用Newton-Raphson方法[14]对式(3)进行亚像素迭代计算，采用双线性插值获得g(x*,y*)的灰度值。迭代完成，将迭代结果代入式(2)，便可得Q*图像坐标值，从而实现与测点Q的对应，实现左右序列图像在不同变形时刻的匹配。

2.2 三维位移计算

如图3所示，假设初始时刻t0，使用ELAS算法对该时刻左、右图像进行分析。利用式(1)测得未变形测点Q的三维坐标(x0,y0z0)。由于结构变形，ti时刻，在左、右序列图像上分别通过DIC获得与初始时刻测点相对应的测点；接着，再次使用ELAS方法可获得变形后测点Q*的三维坐标(xi,yi,xi)，则ti时刻测点Q三维位移如式(4) 所示

(4)

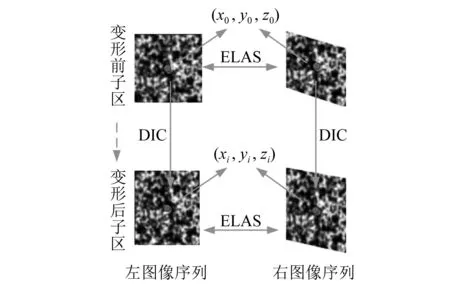
图3 空间三维位移计算流程Fig.3 Flowchart of 3D displacement calculation

3 三层框架倒模型倒塌监测试验

3.1 试验设置

三层框架模型缩尺比为1∶5，如图4(a)所示。三层框架模型柱网尺寸为1.3 m×1.2 m，层高0.7 m，梁柱截面尺寸为80 mm×60 mm，板厚30 mm，选用C30混凝土。三层框架模型底部通过浇筑混凝土承台与振动台连接，承台与振动台台面使用φ22和φ24高强螺栓锚固。试验采用全配重方式。试验使用一维模拟振动台，台面尺寸为4 m×3 m，频率范围为0～40 Hz，最大加速度为1 100 gal，单向电伺服驱动。振动台沿位移计布设方向进行单向振动，如图4(a)所示。

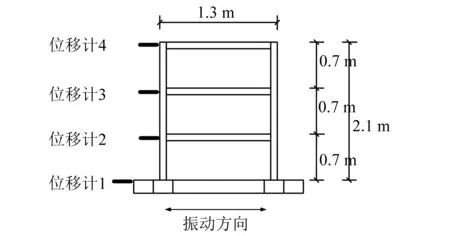
(a) 模型尺寸

(b)试验照片图4 试验设置Fig.4 Experimental setup

本试验采用接触式位移传感器和立体视觉两种方法同时测量三层框架模型的地震反应。位移传感器量程为150.0 mm，精度为0.2 mm，采样频率为1 000 Hz，如图4(b)所示。接触式位移传感器布设于三层框架模型的每一层的左侧纵墙上。为了方便与位移传感器数据进行比较，在三层框架模型的每一层布设直径12 cm的圆形标识点，用于立体视觉方法测量结构变形。

本文使用的立体视觉测量系统选用Pike F-100c系列摄像机，分辨率为1 000×1 000。以上述算法为基础，使用MATLAB语言编译立体视觉三维变形测量软件。试验时，立体视觉测量系统的采样频率设为25 Hz，选用焦距5 mm光学镜头，物距为1.86 m，视场大小为2.45 m× 2.45 m。此外，为保证光线充足，选用1 300 W的卤钨灯作为补充光源。

3.2 试验结果分析

试验时，在模型底部分别输入七种不同加速度峰值El Centro地震波作为激励，加速度峰值分别为80 gal，130 gal，220 gal，370 gal，600 gal，900 gal及1 100 gal，其中1 100 gal重复2次。在第二次1 100 gal的El Centro地震波作用下，框架模型发生倒塌。

3.2.1 370 gal地震波作用

在加速度峰值为80 gal，130 gal，220 gal及370 gal的El Centro地震动作用下，本文方法和位移计同时测得三层框架模型的位移时程曲线。不同加速度峰值的El Centro地震波作用下的各层楼板位移曲线非常相似，只幅值略有差异。因此，本文仅给出加速度峰值为370 gal的El Centro地震波作用下的模型反应，测量结果如图5所示。图中给出结果为相对地面的绝对位移时程曲线。

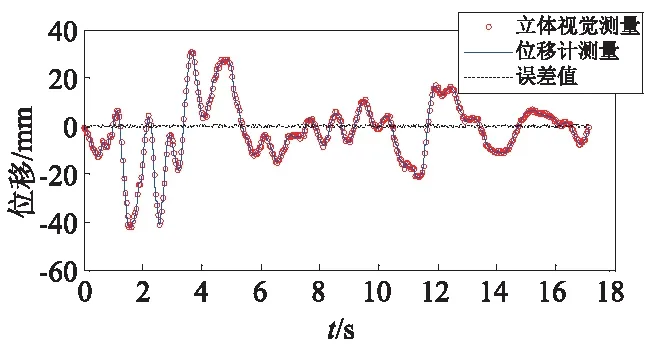
(a) 第一层梁柱节点

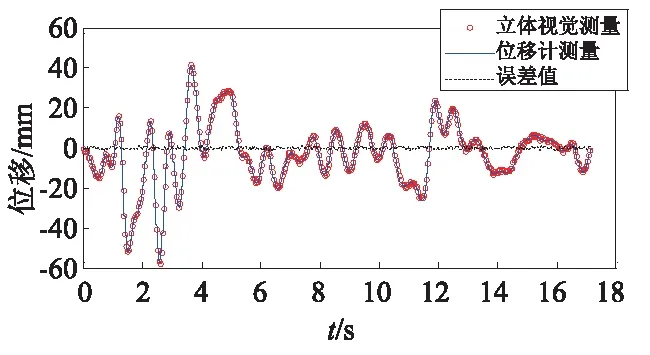
(b) 第二层梁柱节点

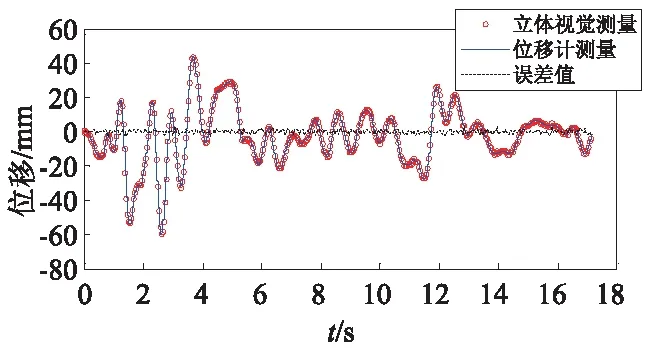
(c) 第三层梁柱节点

由图5可知，模型的一层梁柱节点位移峰值可达30 mm左右，二层楼板和三层梁柱节点达到40 mm及50 mm左右，三层框架模型在370 gal的El Centro地震波作用下将近18 s时停止晃动。 由图5可知，立体视觉方法测得的框架模型的三层梁柱节点位移时程曲线与位移计数据吻合较好，误差均值为0.5 mm左右，证明本文的立体视觉方法的有效性和可靠性。

3.2.2 600 gal地震波作用

考虑到结构大变形时位移计可能损坏，在600 gal El Centro地震波作用下，位移计2和位移计3被撤掉，使用位移计仅测得第三层梁柱节点的位移。而本文的立体视觉方法测得三层框架模型的每层梁柱节点的位移时程曲线，测量结果如图6所示。

由图6可知，本文所提立体视觉方法可同时测得三层梁柱节点的位移时程曲线，而一个位移计仅能测得一层梁柱节点的位移曲线，表明本文立体视觉方法可同时多点进行测量。由图6(c)可知，立体视觉方法测得的三层框架模型的第三层梁柱节点的位移时程曲线与位移计数据吻合很好，误差均值约为0.5 mm，验证本文立体视觉方法的有效性和可靠性。

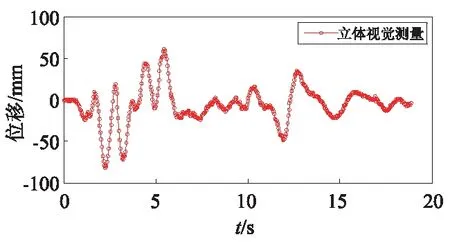
(a) 第一层梁柱节点

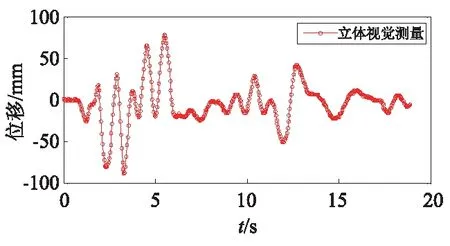
(b) 第二层梁柱节点

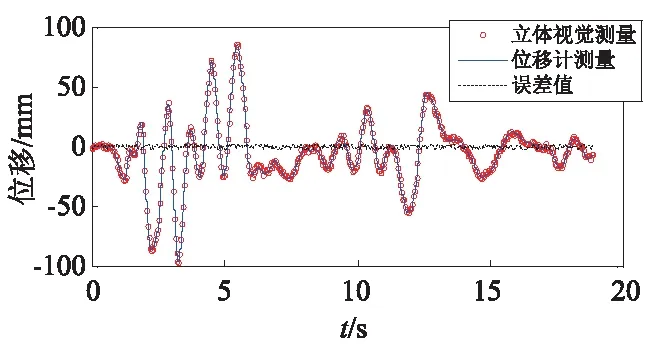
(c) 第三层梁柱节点

3.2.3 1 100 gal地震波作用

在1 100 gal的El Centro地震波作用下，位移计2、位移计3、位移计4均已被撤掉，位移计没有获得任何梁柱节点的变形曲线。三层框架模型的每层梁柱节点位移时程曲线均由本文立体视觉方法测得，测量结果如图7所示。

由图7可知，使用立体视觉方法可同时测得三层梁柱节点的倒塌破坏全程的位移曲线，充分证明本文方法全程监测结构倒塌的可行性。

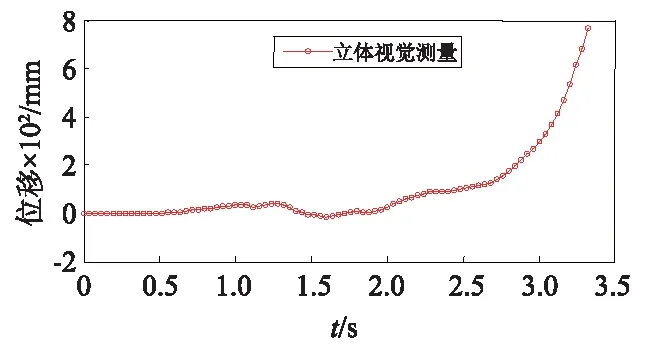
(a) 第一层梁柱节点

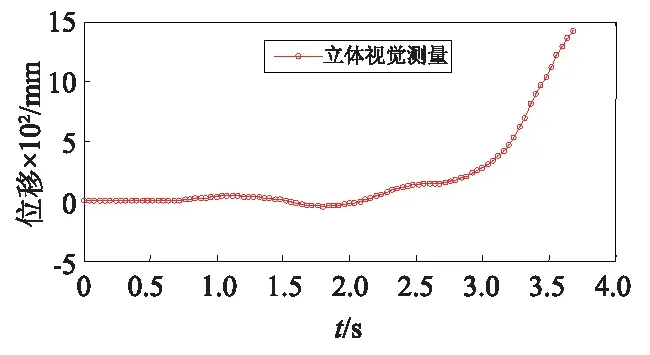
(b) 第二层梁柱节点

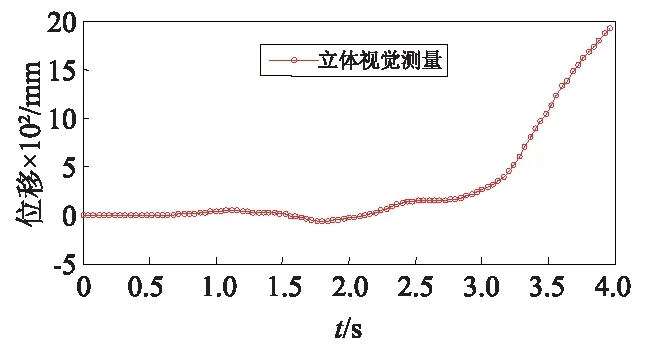
(c) 第三层梁柱节点

在1 100 gal El Centro地震波作用下，三层框架模型的位移在将近3 s的时候开始大幅度增加，表明三层框架模型破坏严重(见图7)，开始倒塌。从第一层梁柱节点到第三层梁柱节点，梁柱节点开始接触地面时间逐渐加大，说明框架模型倒塌的发生是从一层到三层，与实际情况相符。

4 结 论

本文以平行双目视觉模型为基础,组合ELAS及DICM两种算法实现立体匹配及左右序列图像的匹配，由此给出结构三维变形公式。使用立体视觉系统完成不同加速度峰值El Centro地震波作用下三层框架模型振动台试验，测得结构位移时程曲线，并与位移计数据进行比较分析，得到如下结论：

(1) 本文方法与位移计数据吻合较好，验证本文立体视觉方法进行结构动态监测的有效性及可靠性。

(2) 本文通过ELAS与DICM两种算法的组合使用，实现地震波作用下三层框架模型倒塌全程的三维变形监测，证明该方法用于结构大变形全程监测的可行性。

(3) 本文方法独立测得三层框架模型倒塌全程位移曲线，倒塌全程位移数据的获得为结构有限元分析及结构抗震性能分析提供重要依据。

参 考 文 献

[ 1 ] 何庆锋, 刘义仁, 周超, 等. 冲击作用下钢筋混凝土框架抗连续倒塌数值模拟[J]. 振动与冲击, 2016, 35(23): 56-64.

HE Qingfeng, LIU Yiren, ZHOU Chao, et al. Numerical simulationfor progressive collapse of a reinforced concrete frame under impact load [J]. Journal of Vibration and Shock, 2016, 35(23): 56-64.

[ 2 ] 薛志宏. GNSS 动态变形测量关键技术研究[D]. 郑州： 解放军信息工程大学, 2012.

[ 3 ] 冯文灏. 近景摄影测量—物体外形与运动状态的摄影法测定[M]. 武汉: 武汉大学出版社, 2002.

[ 4 ] LUO P F, CHAO Y J, MICHAEL A S, et al. Accurate measurement of three-dimensional displacement in deformable bodies using computer vision[J]. Experimental Mechanics, 1993, 33(2): 123-132.

[ 5 ] 张旭萍，汪家其，张益昕, 等. 大尺度三维几何尺寸立体视觉测量系统实现[J]. 光学学报， 2012， 32(3)： 0315002.

ZHANG Xuping, WANG Jiaqi, ZHANG Yixin, et al. Large scale three-dimensional sterov visio geometric measurement system [J]. Acta Optica Sinica, 2012, 32(3): 0315002.

[ 6 ] CHANG C C, JI Y F. Flexible videogrammetric technique for three-dimensional structural vibration measurement [J]. Journal of Engineering Mechanics, 2007, 133(6): 656-

664.

[ 7 ] MCGINNIS M J, SMITH B, HOLLOMAN M, et al. 3D digital image correlation- an underused asset for structural testing [C]∥Structures Congress of ASCE. Chicago: ASCE, 2012.

[ 8 ] SHAN B H, ZHENG S J, OU J P. Free vibration monitoring experiment of a stayed-cable model based on stereovision[J]. Measurement, 2015, 76(12): 228-239.

[ 9 ] 张广军. 视觉测量[M]. 北京: 科学出版社, 2008.

[10] ZHANG Z Y. A flexible new technique for camera calibration[J]. IEEE Trans. on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330-1334.

[11] GEIGER A, ROSER M, URTASUN R, et al. Efficeint large-scale stereo matching[C]∥Computer Vision-ACCV 2010, Lecture Notes in Computer Science. Berlin: Springer, 2011.

[12] SUTTON M A, MCNEIL S R, HELM J D, et al. Advances in two-dimensional and three-dimensional computer vision [J]. Topics in Applied Physics, 2000, 77(1): 323-372.

[13] 叶南. 基于机器视觉的板料成形性能分析关键技术及系统实现[D]. 南京： 南京航空航天大学, 2010.

[14] BRUCK H A, MCNEIL S R, SUTTON M A, et al. Digital image correlation using Newton-Raphson method of partial differential correlation [J]. Experimental Mechanics, 1989, 29(3): 261-267.