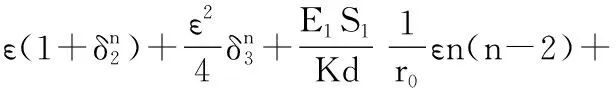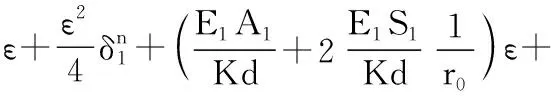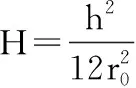环肋椭圆柱壳自由振动分析的一种解析法

方 敏， 朱 翔,2， 李天匀,2， 胡晓芳

(1. 华中科技大学 船舶与海洋工程学院，武汉 430074； 2. 船舶与海洋水动力湖北省重点实验室，武汉 430074； 3. 中国舰船研究设计中心，武汉 430064)

长期以来，圆柱壳结构在工程领域得到了广泛应用，由于肋骨的加强作用,关于环肋柱壳的研究具有重要意义。骆东平等[1]基于Flügge壳体理论和有限差分法系统研究了环肋增强柱壳的自由振动特性；梁斌等[2]在Flügge理论的基础上，考虑流体的影响，分析了水下环肋圆柱壳的固有频率。

随着现代科学技术的发展，椭圆柱壳也被应用于工程实际；另一方面，针对原设计的圆柱壳结构，制造误差[3]，甚至使用环境如深水压力[4]等因素，也会使理想圆柱壳结构的圆形截面产生不可忽略的椭圆度等偏差。与圆柱壳相比椭圆柱壳的解析解或半解析解的获取相对困难一些，因为椭圆截面的曲率半径是一个变量，这使得椭圆柱壳的动力平衡方程为一个变系数的偏微分方程，难以求解。因此关于椭圆柱壳，尤其是加肋椭圆柱壳的振动特性研究开展的并不广泛。Boyd等[5]基于Love和Donnell的薄壳理论对简支椭圆柱壳的自由振动进行了研究，并将结果与早前的两种理论进行了比较，指出Rayleight-Ritzs法对所有范围的椭圆度都相当准确，但是摄动法只在椭圆度小于0.5时是可靠的；Chen等[6]基于Sander壳体理论，采用基于Hamilton准则的模态展开法对有限长椭圆柱壳的自由振动展开了研究，指出该方法较Fourier分析法更为方便，并就多种边界条件对椭圆柱壳自由振动频率的影响进行了分析； Armenakas等[7]基于Flügge壳体理论，讨论了简支椭圆柱壳自由振动的对称和反对称模态，并对比了基于Donnell, Love, Sander壳体理论所得出结果的差异，指出不同壳体理论结果的差异随着椭圆度的增加而增大；熊路等[8-9]基于Love-Timoshenko薄壳理论，采用波传播法以及模态叠加法将位移模式以双Fourier级数形式展开，推导出椭圆柱壳的自由振动方程，并求解了椭圆柱光壳自由振动的固有频率；Boyd等[10]运用Rayleight-Ritzs法讨论了任意边界条件下圆与非圆柱壳加筋与否的振动模态，并分析了环筋与纵梁对振动的贡献程度大小，指出环筋对固有频率的影响要大于纵梁带来的影响；邹时智等[11]基于一类柱壳谐振控制方程呈一阶常微分矩阵方程形式以及傅里叶展开，提出了一种新矩阵方法求解两端简支环肋加强的非圆柱壳在谐外力下的稳态响应；Brodsky等[12]基于Love壳体理论，使用能量原理推导出了两端简支的环肋加强椭圆柱壳的稳定性方程，并表明椭圆柱壳稳定性受环肋的影响类似于圆柱壳，均匀侧向压力下椭圆柱体的屈曲载荷略微超过等效圆柱体的相应值。

本文采用Flügge壳体理论[13]，并采用刚度均摊法考虑环肋与壳体的关系，利用波传播法将壳体位移沿周向和轴向展开成双Fourier级数的形式，并结合Marguerre[14]对于非圆截面曲率半径的处理方法推导出了环肋椭圆柱壳的自由振动方程。为了验证所建立方程和算法程序的准确性，文中将环肋椭圆柱壳退化成环肋圆柱壳和椭圆柱光壳，并将两个退化模型的计算结果与相应参考文献进行了对比分析。深入的研究了椭圆度参数ε，壳肋间距比d/mr0，以及环肋高度a1对环肋椭圆柱壳固有频率的影响。

1 研究对象

图1 环肋椭圆柱壳几何参数及坐标系Fig.1 Geometric parameters and coordinate system of elliptic cylindrical shell with ring stiffeners

无量纲化坐标为

(1)

2 环肋椭圆柱壳自由振动理论模型

2.1 壳体自由振动方程

由Flügge薄壳理论的基本公式出发，并考虑到椭圆截面的曲率半径R(s)是与无量纲周向坐标s有关的函数，可推导出壳体的几何方程以及内力表达式，并将二者带入壳体平衡方程中，便可得到位移形式表达的环肋椭圆柱壳的自由振动方程

(2)

式中： 矩阵[L]3×3的各元素的表达式为

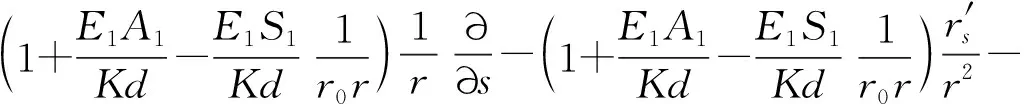
2.2 椭圆截面曲率半径及壳体位移的展开

为了求解式(2)，需将算子Lij(i,j=1,2,3)从变系数形式转换为易于求解的常系数形式，曲率半径r(s)需给出具体形式，根据文献[14],椭圆柱壳曲率半径的无量纲表达形式为

(3)

式中：s为椭圆截面无量纲化的周向弧长坐标，0≤s≤2π；ε为截面的椭圆度参数，为了不产生负曲率，ε不能超过1，定义0≤|ε|≤1，改变ε的正负号只是相当于将壳体沿其对称轴转动π/2弧度，因此，只需考虑椭圆度为正的情况，即0≤ε≤1。对于给定的长短轴a,b，椭圆度参数可表达为[15]

(4)

值得注意的是，椭圆柱壳在周向的对称轴仅有长轴和短轴两条，而圆柱壳则有无数条，故圆柱壳的对称模态和反对称模态的振型相同，这对椭圆柱壳并不成立。因此，对椭圆柱壳的对称模态和反对称模态的变化规律需要分开讨论。壳体各位移在壳体周向是以2π为周期的，将它们在轴向和周向展开成双Fourier级数形式。

对称模态的展开形式为

(5)

反对称模态的展开形式为

(6)

式中：ω为圆频率；m为轴向半波数;n为周向模态阶数；Umn,Vmn,Wmn分别为不同m,n下壳体轴向、周向和径向位移的Fourier系数；λm=kmr0，km为壳体的轴向波数，可根据梁函数推导出其近似值[16]。

将式(3)、式(5)代入平衡方程式(2)中，即可得到三个关于Umn,Vmn,Wmn沿周向模态阶数n相互耦合的新的方程

(7)

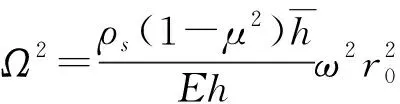
进一步考察式(7)， 其中Fourier系数关于不同周向模态阶数n是相互耦合的，在数值计算时，需对周向模态阶数进行截断处理。当n取有限项数p时，可以得到3p个线性方程，这些方程用矩阵形式表示为

(8)

式中： 当n为奇数时，X=[Um,1Um,3…Um,2p-1⋮Vm,1Vm,3…Vm,2p-1⋮Wm,1Wm,3…Wm,2p-1]T； 当n为偶数时，X=[Um,0Um,2…Um,2p-2⋮Vm,2Vm,4…Vm,2p-2⋮Wm,0Wm,2…Wm,2p-2]T；M为3p阶的实数方阵， 由式(7)中的系数循环而成；I为单位矩阵。

若式(8)中的X有非零解，则要求其系数矩阵行列式值为零，即

|M-Ω2I|=0

(9)

求解式(9)即可求解真空中环肋椭圆柱壳的自由振动固有频率。

3 椭圆柱壳自由振动特性分析

3.1 收敛性分析及算法验证

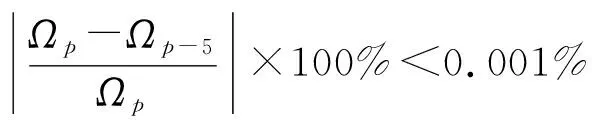
计算的模型参数为：壳厚比h/r0=0.01，壳肋宽度比为b1/mr0=0.02，壳肋高度比为a1/mr0=0.04； 泊松比μ=0.3， 杨氏模量E=E1=2.06×1011Pa；边界条件为壳体两端简支。随着截断项数p的改变，环肋椭圆柱壳自由振动的无量纲固有频率Ω计算结果变化，如图2所示。计算结果收敛时对应的截断项数，如表1所示。

图2 无量纲固有频率的计算值随截断项数的变化(m=1,n=8)Fig.2 The change of the non-dimensional natural frequency versus truncated number(m=1,n=8)

L/mr0d/mr0ε0.20.40.60.81.030.6161618181830.3161618181830.1161618181810.11616181818100.11616181818200.11616181818

由图2可知，随着截断项数p的增大，环肋椭圆柱壳的无量纲固有频率Ω的计算值最终会趋向于一个稳定值；同时，由表1可知，在L/mr0≤20，d/mr0≤0.6的范围内，当取截断项数p=25时，能够保证计算结果收敛，同时也能使计算量不至于过大，本文后续的计算中均取p=25。

为了验证本文建立的控制方程和计算程序的正确性，首先设置ε=0，这样就得到了退化验证的第一个模型。计算了两端简支的退化环肋圆柱壳的自由振动固有频率，并与文献[17]进行了对比验证，本文计算结果与参考文献吻合良好，具体结果见表2。计算模型为L=0.470 9 m,r0= 0.103 7 m,h=0.001 19 m,a1=0.002 91 m,b1=0.002 18 m,d=0.031 4 m，壳体和肋骨材料相同，密度ρ=7 850 kg/m3, 杨氏模量E=2.06×1011Pa， 泊松比为μ=0.3。

表2 两端简支的环肋圆柱壳固有圆频率的对比验证

将肋条的高度a1和b1宽度设为零，这样将环肋椭圆柱壳退化成第二个验证模型，也即无筋椭圆柱壳。计算了两端简支椭圆柱光壳的无量纲固有频率，与基于变分原理求解椭圆柱光壳固有频率的文献[18]进行了对比分析，本文退化结果与文献的结果吻合良好，具体结果见表3。计算模型为h/r0=0.002,μ=0.3,ε=0.5,m=1,E=2.1×1011Pa。这进一步表明本文所建立的理论模型及求解方法的准确性。

同时，本文基于文献[17]的模型参数，通过改变壳体长度，保持环肋数量不变，对椭圆度ε=0.5、不同壳长比的环肋椭圆柱壳的固有频率用商用有限元软件ANSYS进行了计算验证，其中壳体采用SHELL63单元建模，环向肋骨采用BEAM188单元建模。对比验证结果如表4所示，部分FEM计算模态振型图如图3所示。可以看到，本文结果在不同壳长比下的计算结果与有限元结果吻合较好。但同时，在壳长比增大，也即肋骨间距逐渐增大时，两种计算结果的误差也会相应增大，这是因为文中对于环肋的模拟采用了涂抹式的“刚度均摊法”，该方法对于越密、且尺寸越大的加筋结构，结果越准确，而当壳体结构的振动波长远小于肋骨间距时，结果会存在较大误差[19-20]。本文采用的计算模型均考虑了肋骨间距的要求，保证振动波长大于肋距。

表3 椭圆柱光壳的无量纲固有频率对比验证

表4 环肋椭圆柱壳固有频率对比验证

图3 FEM计算的环肋椭圆柱壳模态振型及对应频率Fig.3 Mode shapes and its corresponding natural frequencies of elliptic cylindrical shell with ring stiffeners obtained by FEM

3.2 环肋椭圆柱壳模态振型和固有频率

正如“2.2节”提到的，不同于圆柱壳，由于椭圆柱壳的对称轴仅有长轴和短轴两条，因此有必要分开讨论其对称模态和反对称模态频率。图4给出了本文计算方法得到的不同周向模态阶数的环肋椭圆柱壳的对称和反对称模态振型。与图3对比可见模态吻合良好。

图4 环肋椭圆柱壳的模态振型Fig.4 Mode shapes of elliptic cylindrical shell with ring stiffeners

同时，本文基于文献[17]的模型参数，肋骨高度取a1=0.002 91 m，计算出了两端简支环肋椭圆柱壳轴向半波数m=1的固有圆频率。具体结果见表5，S表示对称模态频率，A表示反对称模态频率。

表5 环肋椭圆柱光壳的固有圆频率

3.3 椭圆度对壳体固有频率的影响

椭圆度是椭圆柱壳区别圆柱壳的一个重要参数，因此，有必要研究环肋椭圆柱壳的固有频率随其椭圆度的变化规律。图5给出了在m=1时， 不同L/mr0及不同d/mr0下，椭圆度ε对两端简支环肋椭圆柱壳固有频率的影响。

(——对称模态；……反对称模态)图5 环肋椭圆柱壳固有频率随椭圆度的变化Fig.5 The change of the natural frequency of elliptic cylindrical shell with ring stiffeners versus ellipticity

从图5可知，环肋椭圆柱壳的固有频率相对于环肋圆柱壳有明显的不同，在同一周向模态阶数n下，壳体的对称模态频率和反对称模态固有频率有所不同，且二者差异随着椭圆度ε的增大而增大；在周向模态阶数n=1,3,5等奇数时，壳体对称模态频率大于反对称模态频率，而在n=2,4,6等偶数时，壳体的反对称模态频率大于其对称模态频率，随着周向模态阶数n的增加，环肋椭圆柱壳的对称模态频率和反对称模态频率的差异逐渐减小；n=0对应的呼吸模态频率都较高，且基本不受椭圆度ε改变的影响；

对比图5(a)～图5(d)可以得出，当壳长比L/mr0一定时，随着壳肋间距比d/mr0的减小也即环肋数量逐渐增大，除了n=0,1外，其他周向模态阶数下环肋椭圆柱壳的对称模态频率和反对称模态频率均有所增大，但二者差异在逐渐减小，在d/mr0≤0.3时，环肋椭圆柱壳的高阶(n≥4)对称和反对称模态频率基本重合；且随着环肋数量的增大，某一椭圆度ε下的环肋椭圆柱壳自由振动基频对应的周向模态阶数也会逐渐降低。

对比图5(e)、图5(c)、图5(f)可以得出，当壳肋间距比d/mr0一定时，随着壳长比L/mr0的增大，环肋椭圆柱壳低阶模态阶数(n≤3)对应的对称模态和反对称模态频率值明显减小，而高阶模态阶数(n≥4)对应的固有频率值变化不大；任意周向模态阶数下的对称模态和反对称模态频率的差异在壳肋间距比d/mr0一定时均随着壳长比L/mr0的增大而减小；且随着壳长比L/mr0的增大，环肋椭圆柱壳自由振动基频对应的周向模态阶数也在逐渐减小。

3.4 环肋间距对壳体固有频率的影响

相邻肋骨之间的距离是影响加肋结构固有属性的重要因素之一，本文采用无量纲参数d/mr0，也即壳肋间距比来讨论肋骨间距的影响。图6给出了环肋椭圆柱壳前6阶周向模态阶数对应的固有频率值随壳肋间距比的变化情况。

(——对称模态；……反对称模态)图6 环肋椭圆柱壳固有频率随壳肋间距比的变化Fig.6 The change of the natural frequency of elliptic cylindrical shell with ring stiffeners versus the non-dimensional stiffeners interval d/mr0

图6(a)是椭圆度ε=0也即环肋圆柱壳固有频率随壳肋间距比d/mr0的变化曲线，图6(b)～图6(d)则是不同椭圆度下的环肋椭圆柱壳固有频率随壳肋间距比的变化曲线。从图6可知，环肋椭圆柱壳固有频率随环肋间距的变化规律与环肋圆柱壳较为相似，环肋间距的改变对周向低阶模态阶数(n≤2)对应的固有频率影响相对较小，对周向中高阶模态阶数(n≥3)对应的固有频率影响较大；随着环肋间距的增大，也即环肋数目减少，周向低阶模态阶数(n≤2)对应的固有频率会逐渐增大，最终趋于一个稳定值，而周向中高阶模态阶数(n≥3)对应的固有频率则明显减小，而且越高的周向模态阶数对应的固有频率减小幅度越大，从模态振型分析，对于低阶模态，环肋以整体参与壳体振动，其质量影响大于其刚度的影响，而对高阶模态，壳体出现了局部弯曲，其刚度影响更大；在椭圆度较小时，随着环肋间距的增大，环肋椭圆柱壳基频对应的周向模态阶数会由n=2往高阶偏移，如在图6(b)中，d/mr0=0.1时，基频对应的周向模态为n=2， 当d/mr0=0.4时，基频对应的周向模态为n=3。

3.5 环肋高度对壳体固有频率的影响

环肋尺寸也是壳体固有频率的因素，本文为讨论方便，在保持环肋宽度不变的情况下，改变环肋高度。图7给出了在环肋宽度b1不变的前提下，环肋椭圆柱壳固有频率值随高度与宽度的比值a1/b1的变化情况。

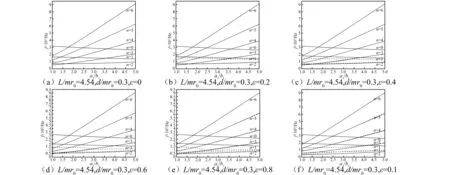
(——对称模态；……反对称模态)图7 环肋椭圆柱壳固有频率随环肋高度的变化Fig.7 The change of the natural frequency of elliptic cylindrical shell with ring stiffeners versus the height of ring stiffeners

图7(a)是椭圆度ε=0也即环肋圆柱壳固有频率随肋骨高度的变化曲线，图7(b)～图7(f)则是不同椭圆度下的环肋椭圆柱壳固有频率随环肋高度的变化曲线。从图7中可以得出，环肋椭圆柱壳固有频率随环肋高度的变化规律与环肋圆柱壳较为相似。低阶模态阶数n=0,1对应的环肋椭圆柱壳对称模态在环肋高度增大后会减小，n=1对应的反对称模态频率则在椭圆度较小(ε<0.6)时随着环肋高度的增加而减小，而在椭圆度较大ε≥0.6时，n=1对应的反对称模态频率则在环肋高度增加到某一值时呈增大趋势，且椭圆度ε越大，该变化对应的高度越小，在ε=1时，n=1对应的反对称模态频率则一直呈增大趋势，这是因为在椭圆度较小时，在环肋高度较低的情况下，环肋的质量影响大于其刚度影响，而随着环肋高度的增加，环肋刚度影响逐渐增大，对于椭圆度较大如ε=1时，环肋刚度影响较其质量影响更大；而n≥3等稍高阶周向模态应的对称模态和反对称频率则随着环肋高度的增大而增大，且越高的周向模态阶数对应的固有频率增大越明显；n≤3时，环肋椭圆柱壳的对称和反对称模态频率的差异随着环肋高度的增大而减小，最终会趋于一致，而n≥4时，对称和反对称模态频率的差异则随着环肋高度的增大而增大；环肋椭圆柱壳基频对应的周向模态阶数也会随着环肋高度的增大而减小。

4 结 论

本文提出了一种求解环肋椭圆柱壳固有频率的解析解法。基于Flügge壳体理论，并采用“刚度均摊”考虑环肋，建立了环肋椭圆柱壳的自由振动方程，计算了不同椭圆度下，两端简支的环肋椭圆柱壳在真空中的自由振动固有频率。较为细致的探讨了壳体椭圆度ε、壳肋间距比d/mr0以及环肋高度a1对环肋椭圆柱壳自由振动的影响，并总结出以下结论：

(1) 在同一周向模态阶数n下，环肋椭圆柱壳体的对称模态频率和反对称模态固有频率值不等，且二者差异随着椭圆度ε的增大而增大；在周向模态阶数n=1,3,5等奇数时，壳体对称模态频率大于反对称模态频率，而在n=2,4,6等偶数时，壳体的反对称模态频率大于其对称模态频率，随着周向模态阶数n的增加，二者差异逐渐减小；而n=0对应的呼吸模态频率不随椭圆度的改变而变化。

(2) 随着环肋间距的增大，也即环肋数目减少，周向低阶模态阶数(n≤2)对应的固有频率会逐渐增大，而周向中高阶模态阶数(n≥3)对应的固有频率则明显减小，且越高的周向模态阶数对应的固有频率减小幅度越大；在椭圆度较小时，随着环肋间距的增大，环肋椭圆柱壳基频对应的周向模态阶数会由n=2往高阶偏移。

(3) 随着环肋高度的增大，低阶模态阶数n=0,1对应的环肋椭圆柱壳对称模态会减小，n=1对应的反对称模态频率则在椭圆度较小(ε<0.6)时减小，而在椭圆度较大ε≥0.6时，n=1对应的反对称模态频率则在环肋高度增加到某一值时呈增加趋势，且椭圆度ε越大，该变化对应的高度越小，在ε=1时，n=1对应的反对称模态频率则一直呈增大趋势；而n≥2等稍高阶周向模态应的对称模态和反对称频率则随着环肋高度的增大而增大，且越高的周向模态阶数对应的固有频率增大越明显；n≤3时，环肋椭圆柱壳的对称和反对称模态频率的差异随着环肋高度的增大而减小，最终会趋于一致，而n≥4时，对称和反对称模态频率的差异则随着环肋高度的增大而增大；环肋椭圆柱壳基频对应的周向模态阶数也会随着环肋高度的增大而减小。

参 考 文 献

[ 1 ] 骆东平,张玉红. 环肋增强柱壳振动特性分析[J]. 中国造船,1989(1): 66-77.

LUO Dongping, ZHANG Yuhong. Analysis of vibration characteristics of ring-stiffened cylindrical shell[J]. Shipbuilding of China,1989(1): 66-77.

[ 2 ] 梁斌, 李戎, 刘小宛,等. 基于波动法的静水压力下环肋圆柱壳耦合振动特性研究[J]. 振动与冲击, 2014,33(21): 142-147.

LIANG Bin, LI Rong, LIU Xiaowan, et al. Coupled vibration of ring-stiffened cylindrical shells under hydrostatic pressure based on wave method[J]. Journal of Vibration and Shock, 2014,33(21): 142-147.

[ 3 ] 张盛,金翔,周桦,等.加肋圆柱壳制造误差对声学性能的影响研究[J].中国舰船研究,2011,6(4): 43-50.

ZHANG Sheng, JIN Xiang, ZHOU Hua, et al. Study on the influence of manufacturing error on the acoustic performance of the stiffened cylindrical shell[J]. Chinese Journal of Ship Research, 2011,6(4): 43-50.

[ 4 ] 赵天奉,段梦兰,杨晓刚,等. 深水导管架桩腿制造误差与抗屈曲特性研究[J].船舶力学,2009,13(2): 241-249.

ZHAO Tianfeng, DUAN Menglan, YANG Xiaogang, et al. Study on manufacturing error and buckling resistance of pile legs in deep water jacket[J]. Journal of Ship Mechanics, 2009,13(2): 241-249.

[ 5 ] BOYD D E, CULBERSON L D. Free vibrations of freely supported oval cylinders[J]. AIAA Journal, 1971,9(8): 1474-1480.

[ 6 ] CHEN Y N, KEMPNER J. Modal method for free vibration of oval cylindrical shells with simply supported or clamped ends[J]. Journal of Applied Mechanics, 1978,45(1): 142-148.

[ 7 ] ARMENAKAS A E, KOUMOUSIS V K. Free vibrations of simply supported cylindrical shells of oval crosssection[J]. AIAA Journal, 1983, 21(7): 1017-1027.

[ 8 ] 熊路,李天匀,朱翔. 基于双Fourier级数表达的椭圆柱壳自由振动特性分析研究[C]//第十四届船舶水下噪声学术讨论会论文集. 重庆：船舶力学学术委员会《船舶力学》编辑部，2013.

[ 9 ] 熊路. 典型非圆截面柱壳的声振固有特性研究[D]. 武汉：华中科技大学, 2014.

[10] BOYD D E, RAO C K P. A theoretical analysis of the free vibrations of ring-and/or stringer-stiffened elliptical cylinders with arbitrary end conditions. Volume 1: Analytical derivation and applications：NASA CR-2151 [R]. [S.l.]: NASA, 1973.

[11] 邹时智, 黄玉盈, 何锃,等. 周向加肋非圆柱壳谐振分析的一个新矩阵方法[J]. 应用数学和力学, 2007,28(10): 1245-1252.

ZOU Shizhi, HUANG Yuying, HE Zeng, et al. A new matrix method for response analysis of circular stiffened non-cylinndrical shell[J]. Applied Mathematics and Mechanics, 2007, 28(10): 1245-1252.

[12] BRODSKY W L, VAFAKOS W P. Buckling analysis of ring-stiffened oval cylindrical shells[J]. Computers & Structures, 1974, 4(6): 1135-1158.

[13] FLÜGGE W. Stress in shells[M]. Berlin:Springer-Verlag, 1973.

[14] MARGUERRE K. Stability of the cylindrical shells of variable curvatur：NASA TM1302 [R]. [S.l.]: NASA, 1951.

[15] ROMANO F, KEMPNER J. Stresses in short noncircular cylindrical shells under lateral pressure[J]. ASME Journal of Applied Mechanics, 1962, 29(4): 669-674.

[16] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403.

[17] BASDEKAS N L, CHI M. Response of oddly-stiffened circular cylindrical shells[J]. Journal of Sound and Vibration, 1971, 17(2): 187-206.

[18] ELSBERND G F, LEISSA A W. The vibrations of non-circular cylindrical shells with initial stresses[J]. Journal of Sound and Vibration, 1973, 29(3): 309-329.

[19] JAFARI A A, BAGHERI M. Free vibration of non-uniformly ring stiffened cylindrical shells using analytical, experimental and numerical methods[J]. Thin-Walled Structures, 2006, 44(1): 82-90.

[20] HAO P, WANG B, LI G, et al. Hybrid optimization of hierarchical stiffened shells based on smeared stiffener method and finite element method[J]. Thin-Walled Structures, 2014, 82: 46-54.

附录：