基于Bayesian证据推断与信息增益的参数化有限元修正模型选择

尹 涛, 王祥宇, 周 越

(武汉大学 土木建筑工程学院，武汉 430072)

经过几十年的发展，有限元分析方法在工程中的应用日益广泛，但由于各种理论假设、边界条件近似性以及几何材料特性参数等不确定性因素影响，致使结构有限元分析模型计算响应与实测结构响应之间不可避免地存在一定偏差。基于试验模态分析方法的有限元模型修正技术正是提高有限元模型精度的有效手段，该方法通过实测低阶模态参数数据进行结构有限元模型修正，从而获得与实际结构较好吻合的修正后有限元模型，并以此为基准模型开展结构响应预测、振动控制、性能评估以及健康监测等领域研究，相关问题已成为目前国内外的研究热点[1-5]。

为求更好地模拟实际结构，开展结构正向分析，人们往往倾向于建立精细的有限元模型，以求细致描述结构各构件局部及结构整体的物理力学特征，这将显著增加结构有限元模型的复杂程度，直接导致过于庞大的有限元模型规模。事实上，结构有限元模型修正过程可视为带约束的参数优化过程，其在优化算法框架内，通过迭代计算不断调模型参数，使有限元模型的计算响应输出与实测数据之间的误差达到极小，属于典型的结构动力学反问题范畴。但在实际应用中，过于复杂的有限元模型会造成至少两方面不利影响。一方面，过于庞大的模型规模非常不利于动力学反问题优化分析过程中的反复迭代计算；另一方面，受传感器通道数量、测量噪声以及高阶模态获取困难等因素制约，实际获得用于有限元模型修正的有效测量信息相对于模型待修正参数往往不足，使得模型参数修正过程容易出现病态，同时也会显著增加待识别模型参数相对于模型误差及测量噪声等不确定性因素的敏感性，容易出现所谓‘过拟合’问题[6]，而这对含有大量待定模型参数的复杂有限元模型尤其如此。因此，在保持有限元模型计算响应与结构实测响应吻合程度条件下，如何有效降低有限元分析模型的参数化复杂程度，值得进一步研究。

目前常采用敏感性分析方法来进行有限元模型参数选择，以减少待修正模型参数数量，即通常选择对结构响应敏感性较大的模型参数作为待修正参数[7-12]。但对于规模较大的结构模型，该敏感性分析方法所选取的模型参数并不一定能很好地用作待修正参数[13]。针对有限元模型修正中的待定参数选择问题，本文以概率论和信息论为基础，发展一种基于Bayesian证据推断与马尔科夫链蒙特卡洛(Markov Chain Monte Carlo，MCMC)法相结合的有限元修正模型选择分析方法。通过引入信息增益(Information Divergence)或KL散度(Kullback-Leibler Divergence)[14]指标(该指标在本文具体指从实测数据中提取用于未知模型参数修正的信息量多少)，对有限元模型待修正参数的复杂程度进行惩罚，从而在有限元模型建模参数复杂性与其相应信息论复杂性之间获得平衡，最终获得满足模型与实测数据吻合度的相对简单有限元修正模型，有效避免由于待修正参数过多而导致的模型过拟合问题。通过某两层螺栓连接框架结构有限元模型修正的数值仿真与实验室模型试验研究，对本文方法正确性与有效性进行验证。

1 基本理论

1.1 Bayesian多模型证据推断

考虑目标结构存在NC种可能的有限元参数化建模方式(或称之为模型类别)，分别定义为C1, C2, …, CNC。本文假定各有限元模型类别之间通过不同的建模参数进行区分，即第j个模型类别Cj(θj)通过其待估参数向量θj来描述，θj=θj(Θj)为模型参数空间Θj⊂RNj中的向量，Nj表示向量θj所含模型参数的数目。基于Bayes定理，在给定测量数据D的条件下，模型类别Cj的后验概率密度函数可以表示为

(1)

式中：U为使用者对于各模型类别Cj先验概率密度函数p(Cj|U)(j=1,2,…,NC)的经验判断；其满足

(2)

式(1)中分子项p(D|U)可由全概率公式给出

(3)

式中：D为从目标结构获得的测量数据集合，本文具体指Ns组重复测量得到的前Nm阶固有频率与模态振型，即

(4)

此外，式(1)中p(D|Cj,U)表示模型类别Cj在给定数据集D条件下的证据，忽略用户经验判断U，并结合此前模型类别定义，该证据项可以通过全概率积分形式表示为

(5)

式中：p(θj|Cj)为对于指定模型类别Cj，定义在其模型参数空间Θj中参数向量θj的先验概率密度函数；对于本文考虑的有限元模型修正问题，假定该先验概率服从高斯分布。p(D|θj,Cj)为给定数据集D和模型类别Cj条件下的似然函数，即

(6)

式中：J(θj;D,Cj)为有限元模型类别Cj在给定模型参数θj条件下的固有频率、模态振型计算值与Ns组测量值之间的误差函数，且假定该误差服从均值0、方差为σ2的独立高斯分布，即

(7)

依据Bayes定理，在给定测量数据集D与模型类Cj条件下，模型参数θj的后验概率密度函数可以表示为

(8)

式中：等式右边分母项p(D|Cj)即为式(5)给出的证据因子。

为方便，取证据因子的对数形式进行计算，即对式(5)两边同时取对数，可得

(9)

考虑式(8)所给出的后验概率分布，式(9)等号右边可以进一步表示为

(10)

式中：等号右边两个数学期望式分别为

(11)

与

(12)

式(11)反映有限元模型类别Cj的计算数据与实际测量数据的平均吻合程度，即该值越大，表示有限元模型与实测数据越符合。式(12)称为KL散度或信息增益，其表示对含模型参数θj的有限元模型类Cj进行修正时所需要从测量数据集D中提取的信息量多少，该值恒为非负，且其取较大值时表明对Cj类模型进行修正时需要提取的信息量多。事实上，有限元模型修正过程为特征值反问题求解过程，与函数拟合过程类似，并非模型越复杂越好，过于复杂的模型有时会造成对实测数据的‘过拟合’问题，过度拟合了实测数据中的噪声，而式(12)中给出的信息增益量度能够较合理地对模型复杂程度进行惩罚，这在后面的数值仿真与模型实验部分中将获得验证。

1.2 基于后验分布中MH抽样的数学期望值估计

Metropolis Hasting(MH)是蒙特卡罗马尔科夫链(MCMC)方法中一类重要的抽样方法[15]。本文采用该方法分别计算式(11)与式(12)在后验分布p(θj|D,Cj)中定义的多重数值积分，获得以数学期望值表示的模型数据吻合度与信息增益，从而通过式(10)得到模型类别Cj以对数形式表达的证据因子。

(13)

(14)

(15)

(16)

此时，式(9)中对数形式的证据因子ln[p(D|Cj) ]可以通过对以上两个数学期望值求差获得，因而，式(1)中给出的有限元模型类别Cj的后验分布则可以通过下式计算为[16]

(17)

式中，M为ln[p(D|Cj) ]在所有模型类别Cj(j=1,2,…,NC)中的最大值。模型后验概率p(Cj|D)从概率论角度对有限元修正模型的合理选择进行解释，即某类有限元模型Cj的后验概率值越大，表明该类候选模型选作有限元修正模型的可能性越高。

2 数值仿真研究

2.1 框架模型介绍

为验证本文方法，对某两层平面螺栓钢框架进行数值仿真研究，如图1(a)所示。其中，梁-柱与柱-基础均采用螺栓连接，模型共4个梁-柱连接部位及2个柱-基础连接部位。该框架梁柱均采用10#工字钢，其几何与材料特性参数分别为：杨氏模量E=2.01×1011N/m2，质量密度ρ=7.85×103kg/m3，截面面积A=1.57×10-3m2及截面惯性矩I=2.21×10-6m4。该两层框架模型中梁-柱及柱-基础节点均视为半刚性连接，其转动刚度采用端部短梁的抗弯刚度来模拟，并通过调整端部短梁的抗弯刚度来模拟螺栓连接松紧程度。

此框架有限元离散模型示意图及相应测量节点与方向编号，如图1(b)所示。共有30个单元、30个节点以及84个自由度，6个半刚性节点，且在其中8个自由度方向上布置模态拾振点。取该框架结构前4阶模态频率与振型进仿真计算，对计算频率与振型分别施加标

图1 两层螺栓框架的模型图Fig.1 Schematic model of two-storey bolt-connected frame

准差为1%与10%的高斯白噪声以模拟测量噪声情况，且假定通过重复测量共获得30组模态参数数据，即Nm=4，Ns=30。

本算例将此框架结构中所有螺栓半刚性连接的转动刚度k1,k2,…,k6均视为待修正参数，如图2所示。NC=6类有限元模型。从C1～C6，模型所含建模参数逐渐增多，即模型复杂程度相应逐渐增加。具体地，C1为相对最简单模型，其表示所有半刚性连接均采用相同的单一模型参数θ1进行修正。C2含两个建模参数θ1与θ2，其分别修正所有柱-基础连接刚度与梁-柱连接刚度。C3通过3个建模参数θ1，θ2与θ3分别修正所有柱-基础连接刚度与各层梁-柱连接刚度。在C3基础上，C4进一步区分左、右柱的柱-基础连接刚度，继续增加了模型的复杂程度。C5在C3基础上，进一步将各层左、右柱的梁-柱连接刚度区别开来，共含有θ1～θ5此5个建模参数。C6在C5基础上进一步对左、右柱-基础连接刚度k1和k2进行区分，共包含6个模型参数，且该类模型为本算例所考虑的相对最复杂有限元参数化模型类别。

图2 所考虑的各有限元模型类Fig.2 Different classesof FE models considered

此外，本模型算例共考虑5种仿真工况，各工况具体设置情况，如表1所示。其中kb与kbc分别表示柱-基础与梁-柱半刚性连接刚度值，本例分别取为0.03EI与0.06EI。工况1为基准状态情况，即所有梁-柱及柱-基础半刚性连接刚度均分别取为各自基准值；工况2基于基准状态，将首层左侧梁-柱连接刚度值k3降低为其基准状态值的0.7倍；工况3在基准工况下，将左侧柱-基础连接刚度k1取为其基准状态值的0.7倍；工况4进一步考虑两处梁-柱连接松动情况，即在工况2基础上，将第二层右侧梁-柱连接刚度k6值进行降低；工况5将工况2与工况3中的半刚性节点松动情况进行组合，即研究左侧柱-基础连接刚度k1与第一层左侧梁-柱连接刚度k3同时发生降低的情况。

表1 数值仿真工况设置

MCMC算法模拟次数设为10 000，且先验分布中各模型参数均服从以基准状态值为均值、标准差为0.3的正态分布，使模型参数空间定义在给定的(0,2]范围内。以工况2为例，图3为此工况下模型类C2中模型参数θ1与θ2的MCMC采样历程。从图3可知，在采样历程中，模型参数θ1与θ2的值围绕各自均值在较小范围内波动。同时，梁-柱连接刚度的整体模型参数θ2值略小于1，这与工况2中所定义的框架第一层左侧梁-柱连接刚度值k3降低的事实相符(参见表1与图2)。此外，模型参数θ1偏离均值的离散度较θ2大，表明该两层螺栓框架结构中柱-基础连接刚度的不确定性程度较梁-柱连接刚度大，其与文献[17]中的有关研究结果规律相符(见图3)。

图3 仿真工况2下模型类C2中建模参数的MCMC采样历程Fig.3 MCMC sampling history of modeling parameters in C2for case 2

图4给出工况2下，模型类C2中模型参数θ1与θ2的联合先验分布与后验分布情况对比。从图4可知，后验分布范围仅占先验分布的一部分，经过Bayesian更新，模型参数θ1与θ2的不确定性程度明显降低，或者说在有限元模型修正过程中，算法从先验分布中提取了部分有用信息用于对于模型参数θ1与θ2的更新，依式(12)之定义，其反映从数据D中提取的关于模型类C2的信息增益大小。此外，模型参数θ1的不确定性较θ2大，这与图3中的结果相符(见图4)。

图4 工况2中模型类C2中建模参数的联合先验与后验分布Fig.4 Jointed prior and posterior distributions of modeling parameters in C2 for case 2

采用本文方法对表1中所列各仿真工况进行有限元修正模型选择研究，分别计算各工况下各类有限元模型的数据吻合度(式(11))、信息增益(式(12))、对数形式的证据因子ln[p(D|Cj) ](式(10))以及后验概率p(Cj|D)(式(17))，计算结果列于表2，其中，最优模型相关数据用粗体表示。对于工况1，本文方法给出的最优有限元模型类别为C1，其为所有考虑模型类别中最简单的一类。这表明在基准状态情况下，对本例仅单个参数就足够修正该有限元模型，而并非模型越复杂越好。

表2 各数值工况下模型选择结果

在工况2下，由于其在基准状态基础上对两层框架第一层左侧梁-柱连接刚度值k3进行了局部调整，相比于工况1，工况2理论上需要较多的模型参数才能更好地对该局部刚度改变进行刻画，因而本文方法确定C3为最优模型类的结论符合上述推断。同时，从表2给出的工况2计算结果中还可知，随着模型复杂程度增加，即模型参数逐渐增多，有限元模型修正过程就需要从数据D中提取更多的信息用于修正这些额外增加的模型参数，表现在信息增益指标变大。该信息增益指标又反过来对模型的复杂程度起到一定的惩罚作用。例如，工况2中C4与C5两类模型复杂程度均较C3高，因而相应的信息增益也逐渐增加，表明需要提取更多信息来修正C4与C5中较多的模型参数。但信息增益也并非一定随着模型复杂程度增加而单调增大，例如，此工况下的C6类模型，其复杂程度相对最高，但对其进行模型修正所需提取的信息量却较相对简单的C5类模型少。此外，还应指出，在工况2下，虽然模型类C2较C3简单，其也将梁-柱连接刚度与柱-基础连接刚度区分开(见图2)，但由于其并未进一步区分框架第一层与第二层梁-柱连接刚度，难以细致刻画仅由k3引起的第一层局部刚度改变，因而，造成模型类C2的数据吻合度相对C3差很多(对比表2中工况2的第2、第3行结果)，因此，尽管修正C2类模型所需提取的信息量较C3类模型相对要少，但综合来看，模型类C3的证据因子较C2大很多，其导致C3类模型以34.63%的后验概率p(Cj|D)被选中，而C2类模型被选中的概率仅为0.34%。

表2中所列其余3种工况的计算结果规律与工况1、工况2类似，且对于不同工况，在数据吻合度基本相同条件下，有限元模型修正过程均倾向于选择较为简单的参数化模型类别。此外，图5综合给出了所有计算工况下各类模型的后验概率p(Cj|D)，从图5可知，在综合考虑信息论表达复杂性条件下，数据吻合程度接近情况下，复杂程度相对较低的参数化模型类别对于有限元模型修正更为适合。

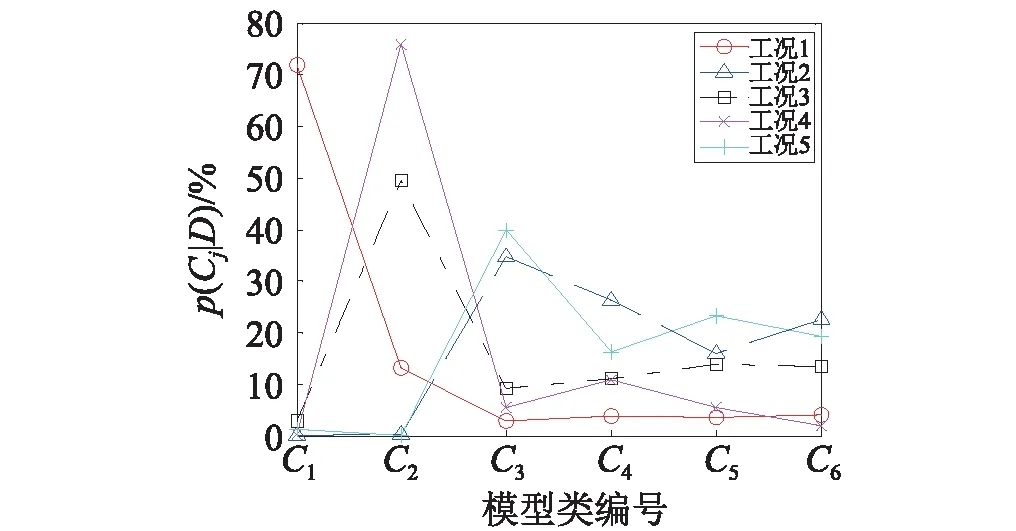
图5 各仿真工况下 p(Cj |D)的结果对比Fig.5 Comparison of simulation results of p(Cj |D) for all cases

3 实验验证

通过实验室螺栓框架结构模型进一步验证本文方法，该实验钢框架几何尺寸与材料特性均与此前数值仿真所采用的框架模型对应，同样由4根10#工字型钢组成，梁-柱通过角钢与螺栓进行连接，而柱-基础则通过柱底端部焊接钢板与基础进行螺栓连接，通过扳手控制螺栓松紧程度，本实验框架整体与连接细部如图6所示。

模态试验中传感器布设位置及方向亦与此前数值仿真保持一致，通过冲击力锤施加框架平面内的水平向瞬态激励(见图6(e))。利用MPS-140801-IEPE信号采集卡将采集到的结构加速度自由响应信号通过USB端口传输到PC机，采用MPS-140801 Date Acquisition软件动态显示并存储信号，再通过自编NExT-ERA模态识别程序[18-19]获得框架结构的前4阶固有频率与模态振型，其中，采样频率设为1 000 Hz，采样时长为10 s。保持激励位置与方向不变，基准状态下重复进行多次模态试验，并获得Ns=15组模态参数，其中，前4阶固有频率的平均值分别为：17.59 Hz，77.76 Hz，148.85 Hz及159.80 Hz。通过扳手松动框架第一层左侧梁-柱连接上部角钢的一对螺栓，如图6(d)所示。如图7所示，并保持此前激励方式，通过重复模态试验获得此状态下的15组模态参数，且前4阶模态频率均值分别为：16.72 Hz，77.41 Hz，148.74 Hz及157.02 Hz。

图6 两层螺栓框架实验模型Fig.6 Experimental two-storey bolt-connected steel frame

图7 两层实验框架螺栓松动部位图Fig.7 Bolt-loosening location of the two-storey laboratory frame

基于模态试验测得的两种状态下Ns组模态参数数据，采用本文方法进行实验框架结构的有限元模型选择研究，其中MCMC算法的控制参数设置与数值仿真一致。对该实验框架考虑两种工况，即基准状态工况与梁-柱连接部位局部螺栓松动工况，其分别与数值仿真中的前两种工况相对应，计算结果列于表3。与表2所列项目相同，表3分别给出两种工况下各类有限元模型的数据吻合度、信息增益、证据因子及后验概率。对于实验工况1，通过本文方法确定的最优有限元参数化模型类别为所考虑的最简单模型C1，其与数值仿真工况1结果相符，表明基准状态条件下，有限元模型修正倾向于选择相对最简单的参数化分析模型。同时，该实验工况1的结果还可以看出，对相对最复杂模型类别C6(含6个模型参数)的修正所需从实测数据D中提取的信息量，比相对简单的含3参数的C3类模型更少；因而，在两者模型数据吻合程度接近的情况下，C6类模型的证据因子(或后验概率)较C3更大，表明此状态下C6类模型相对C3较优。

表3 实验工况下模型选择结果

实验工况2考虑第一层左侧梁-柱半刚性连接局部螺栓松动情况(见图7)，其计算结果也表现出与仿真工况2相似的规律。从表3可知，模型类别C3的后验概率最大，被确定为此工况下的最优模型类别。同时，也可以看出，在此局部刚度变化情况下，有限元模型修正倾向于选择相对较复杂的参数化模型类别，以较好地反映该局部刚度变化特征。但从信息论复杂度表征角度来看，在数据吻合程度类似条件，过于复杂的参数化模型反而不利于模型修正，因为此时需要从实测数据D中提取的信息量最多，其对模型复杂程度的增加起到惩罚作用。例如，表3工况2中，模型类C3与C4数据吻合程度很相近，但由于C4在修正过程中需要提取更多信息，导致其最终的证据因子或后验概率比C3小。

此外，为更直观地比较实验与数值仿真结果，图8分别比较了实验与仿真条件下工况1与工况2中各类模型的后验概率p(Cj|D)，从图8可知，两者吻合程度较好，反映出实验结果与数值仿真的一致性，进一步验证了本文方法的合理性与正确性。

图8 模型后验概率p(Cj |D)的数值仿真与试验结果对比Fig. 8 Comparison between simulation and experiment results of model posterior PDF p(Cj |D)

4 结 论

本文基于Bayesian证据推断理论与信息增益指标，并结合MCMC中的Metropolis Hastings抽样法，对有限元参数化模型修正中待定模型参数的选择问题进行研究，通过对某两层螺栓连接钢框架有限元模型修正进行数值仿真与实验室模型试验研究，结果表明：本文方法通过信息增益指标定量表征有限元模型修正过程从测量数据中提取用于修正待定模型参数的信息量大小，以惩罚有限元模型待修正参数的参数化复杂程度，能有效权衡有限元模型建模参数复杂程度与其相应的信息论表征复杂度，以获得模型参数化相对较简单的待修正有限元模型。此外，对于本文螺栓连接框架结构而言，柱-基础半刚性连接模型参数的不确定性较梁-柱半刚性连接的不确定性更大，对结构整体特性影响也相应更显著，这在该类型结构的实际工程设计过程中需要予以注意。应注意到，待修正模型参数先验分布形式会对信息增益计算结果产生影响，其选取主要依赖使用者经验，本文选取满足最大熵原理和中心极限定律的正态分布作为有限元待修正模型参数先验分布形式，有关模型参数先验分布影响规律将在后面的研究中予以进一步探讨。

参 考 文 献

[ 1 ] FRISWELL M I, MOTTERSHEAD J E. Finite element model updating in structural dynamics[M]. Dordrecht: Kluwer Academic Publishers, 1995.

[ 2 ] 张德文, 魏阜旋. 模型修正与破损诊断[M]. 北京：科学出版社, 1999.

[ 3 ] 魏来生. 结构有限元动态模型修正方法综述[J]. 振动与冲击, 1998, 17(3): 43-46.

WEI Laisheng.A review on the updating methods of finite element model[J]. Journal of Vibration and Shock, 1998, 17(3): 43-46.

[ 4 ] 尹涛, 余岭, 朱宏平. 一种基于模型修正的结构损伤识别方法[J]. 振动与冲击, 2007, 26(6): 59-62.

YIN Tao, YU Ling, ZHU Hongping.Model updating based approach for structural damage detection[J]. Journal of Vibration and Shock, 2007, 26(6): 59-62.

[ 5 ] YU L，YIN T. Damage identification in frame structures based on FE model updating[J]. Journal of Vibration and Acoustics, 2010, 132(5): 1741-1757.

[ 6 ] BECK J L. Bayesian system identification based on probability logic[J]. Structural Control and Health Monitoring, 2010, 17(7): 825-847.

[ 7 ] FRISWELL M I, MOTTERSHEAD J E, AHMADIAN H. Combining subset selection and parameter constraints in model updating[J]. Journal of Vibration and Acoustics, 1998, 120(4): 854-859.

[ 8 ] 宋汉文, 王丽炜, 王文亮. 有限元模型修正中若干重要问题[J]. 振动与冲击, 2003, 22(4): 68-71.

SONG Hanwen, WANG Liwei, WANG Wenliang.Several important problems for updating finite element model[J]. Journal of Vibration and Shock, 2003, 22(4): 68-71.

[ 9 ] 费庆国, 张令弥, 李爱群, 等. 基于统计分析技术的有限元模型修正研究[J]. 振动与冲击, 2005, 24(3): 23-26.

FEI Qingguo, ZHANG Lingmi, LI Aiqun, et al. Finite element model updating using statistics analysis[J]. Journal of Vibration and Shock, 2005, 24(3): 23-26.

[10] 李延强, 杜彦良. 基于最敏感设计参数的斜拉索有限元动力模型修正[J]. 振动与冲击, 2009, 28(3): 141-143.

LI Yanqiang, DU Yanliang. Dynamic finite element model updating of stay-cable based on the most sensitivity design variable[J]. Journal of Vibration and Shock, 2009, 28(3): 141-143.

[11] MOTTERSHEAD J E, LINK M, FRISWELL M I. The sensitivity method in finite element model updating: a tutorial[J]. Mechanical Systems and Signal Processing, 2011, 25(7): 2275-2296.

[12] WAN H P, REN W X. Parameter selection in finite-element-model updating by global sensitivity analysis using Gaussian process metamodel[J]. Journal of Structural Engineering, 2014, 141(6): 04014164.

[13] 姜东, 丁继锋, 费庆国，等. 一种有限元模型修正中的参数选择方法[C]∥2010全国固体力学大会. 武汉：固体力学学报, 2011.

[14] GULL S F. Bayesian inductive inference and maximum entropy[C]∥ In Maximum Entropy and Bayesian Methods. Dordrecht: Kluwer Academic Publishers, 1989.

[15] HAARIO H, LAINE M, MIRA A, et al. DRAM: efficient adaptive MCMC[J]. Statistics and Computing, 2006, 16(4): 339-354.

[16] YUEN K V. Bayesian methods for structural dynamics and civil engineering[M]. Hoboken: John Wiley & Sons, 2010.

[17] YIN T, JIANG Q H, YUEN K V. Vibration-based damage detection for structural connections using incomplete modal data by Bayesian approach and model reduction technique[J]. Engineering Structures, 2017, 132(1): 260-277.

[18] YIN T, LAM H F, CHOW H M, et al. Dynamic reduction based structural damage detection of transmission tower utilizing ambient vibration data[J]. Engineering Structures, 2009, 31(9): 2009-2019.

[19] LAM H F, YIN T. Dynamic reduction based structural damage detection of transmission towers: practical issues and experimental verification[J]. Engineering Structures, 2011, 33(5): 1459-1478.