水泥砂浆的平板撞击实验与高压状态方程研究

高 飞， 王明洋， 张先锋，熊 玮， 邹慧辉， 文 祝

(1. 南京理工大学 智能弹药国防重点学科实验室，南京 210094; 2. 解放军理工大学 爆炸冲击防灾减灾国家重点实验室，南京 210007 )

水泥砂浆为构成混凝土的基体材料，无论是军事领域还是民用领域都广泛使用。在军事领域，绝大多数军事工事都是由混凝土构造的，譬如指挥所、飞机库等；在民用领域，混凝土可浇筑成核设施保护层、桥梁等。但在战时和恐怖袭击条件下，这些工程往往会面临爆炸与冲击载荷的破坏。因此，水泥砂浆或混凝土在强动载作用下的动态特性研究对重大工程安全防护和钻地武器战斗部设计具有重要的工程应用背景和科学研究价值。

在强动载作用下，防护结构处于数百兆帕到数十吉帕甚至更高的压力状态时，混凝土可看作可压缩流体，其本构方程表示为静水压力与体应变的关系，即高压状态方程。很多学者采用平板撞击实验技术研究了混凝土的冲击波传播特性[1-2]、冲击绝热关系[3-4]、高压状态方程[5-6]、本构关系[7-8]等相关内容。施绍裘等[9-10]采用改进的分离式霍普金森压杆(Split Hopkinson Pressure Bar, SHPB)被动围压试验方法和平板撞击试验对水泥砂浆在准一维应变和一维应变下的应力-应变关系与高压下静水压曲线进行了比较研究。Wang 等[11]采用SHPB实验技术对水泥砂浆在高应变率下的动态响应进行了研究，结果表明水泥砂浆是一种含内部损伤的非线性率相关材料，且对围压效应较敏感。Grote等[12]对无围压强度为46 MPa的水泥砂浆分别进行了SHPB实验和平板撞击实验，SHPB实验结果表明，当应变率为1 700 s-1时材料的流动应力是静态强度的4倍，平板撞击实验结果表明，330 m/s的撞击速度下材料的平均流动应力达到了1.3 GPa。Tsembelis等[13]通过应力计对水泥砂浆的剪应力强度和失效破坏进行了研究。Tsembelis认为应力超过Hugoniot弹性极限(Hugoniot Elestic Limit, HEL)时，水泥砂浆材料呈非弹性行为，伴随着孔隙坍塌和破坏，材料的强度会进一步降低，而且随着围压的增加剪应力将有所增加。Riedel等[14]对强度为35 MPa和140 MPa的混凝土及水泥砂浆进行了冲击压缩特性研究，分别采用P-α状态方程和Mie-Grüneisen型冲击状态方程描述材料的孔隙压实过程和基体的压缩。尽管对水泥砂浆的动态力学性能已有部分研究结果，但是对其冲击绝热关系及状态方程的研究国内还不多，主要工作还是针对混凝土材料。

本文采用火药枪装置和PVDF(Polyvinylidene Fluoride)应力测试技术，对强度约40 MPa的水泥砂浆在一维应变条件下的冲击波传播特性、冲击绝热关系及状态方程进行研究，重点围绕材料的微损伤对冲击波的传播规律和冲击绝热关系的影响展开论述，揭示冲击波衰减规律的细观物理本质，对材料的冲击压缩特性采用P-α状态方程和Mie-Grüneisen型多项式状态方程分段描述，明晰了多孔介质从孔隙压缩到基体压缩的完整过程。

1 试样与实验装置

1.1 试样制备与试样参数

水泥砂浆试样采用P.O42.5普通硅酸盐水泥、中砂和水按一定的配合比例(水泥、砂、水的质量之比为1∶1∶0.4)经混合搅拌均匀、注模、振动、凝固而成，脱模后，养护28 d后经过切割和端面打磨等工序制作成尺寸约Φ48 mm×8 mm的水泥砂浆试样，端面平行度0.05 mm以内，表面平整度在0.02 mm以内，试样的密度实测约为2.10 g/cm3。通过3个尺寸为150 mm的立方块单轴压缩实验，测得水泥砂浆的单轴抗压强度为41.8 MPa (3个试样的平均值)。表1为编号为M1-1～M7-2的14个试样的相关参数，表中从上到下每两个试样为1组，组成实验编号为001～007的7组试样，每组试样中单个试样的厚度相近。

表1 Φ48 mm×8 mm砂浆试件参数

1.2 实验装置与测试方法

平板撞击实验在内径为50 mm的火药发射枪上进行，装置如图1 所示。利用枪口处的线圈靶和测时仪对飞片进行速度捕捉，试件部分主要由外壳、保护板、传感器和试件组成(见图2)。实验中，飞片速度范围：250～450 m/s，在弹托的驱动下，飞片与待测试件碰撞并产生一维应变波，利用试件中不同位置处的PVDF传感器来记录应力波的传播信息。组装完成的水泥砂浆样品，如图3所示。

实验过程参数见表2，PVDF可测到两处的电压-时间波形，通过2个51 Ω的并联电阻、PVDF灵敏度系数K及敏感元面积A，可得到实验中试件的冲击波波后应力。

图1 水泥砂浆平板撞击实验装置布局Fig. 1 Arrangement of the planar impact experiment setup

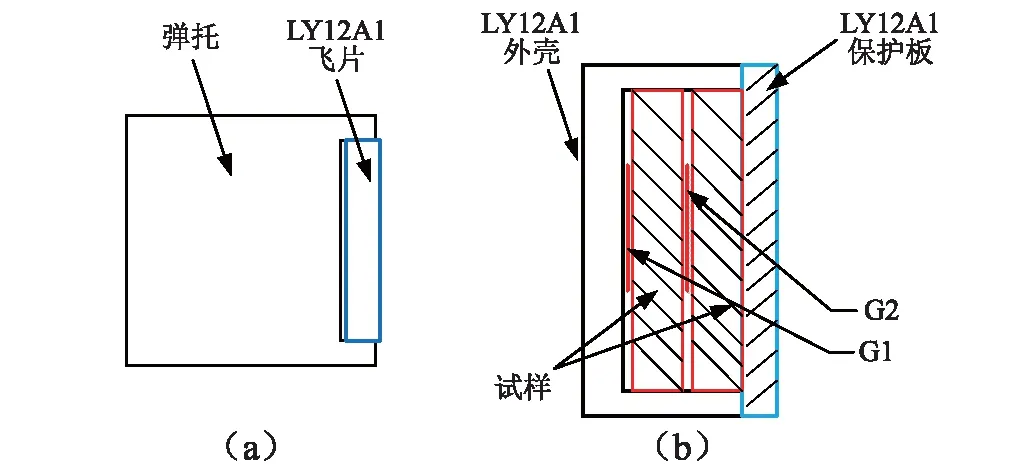
图2 水泥砂浆平板撞击实验装置示意图Fig. 2 Schematic of cement mortar samplesfor planar impact experiment

图3 组装好的水泥砂浆待测组件Fig. 3 Photograph of fabricated cement mortar samples

实验编号弹速/(m·s-1)飞片厚度/mm铝外壳厚度/mmR1/ΩR2/Ω001323.624.942.905151002257.074.962.885151003281.694.922.905151004369.004.922.865151005393.704.942.885151006439.604.922.905151007318.474.962.925151

1.3 PVDF动态标定

为了使用和实际工况相近的K值，采用对称撞击法获得高压区动态灵敏度系数，文中选用电流模式进行标定。电流模式[15]是将一个阻抗较低的电阻并联在传感器的两端，构成放电电路，传感器两端产生的电荷经过电阻R形成电流。通过测量外接电阻R两端的电压，可以得到电流的变化情况，电流对时间积分就可以求出PVDF传感器产生的电荷量。具体步骤如下：

将图2中的试样换成Φ48 mm×8 mm的LY12铝合金，根据LY12铝合金的冲击波速度D与粒子速度u的关系[16]D= 5.33+1.34u，单位为km/s。平面对称碰撞条件下，粒子速度约等于飞片撞击速度的一半，由此易得应力峰值P，并利用如下关系式求得电荷量Q和灵敏度系数K

(1)

(2)

式中：V(t)为时间-电压信号；R并联电阻值；A=1 cm×4 cm = 4 cm2为传感器敏感元面积；q为单位面积上的电荷量。

将不同速度下的数据点通过线性拟合得到q-P关系的斜率，即动态灵敏度系数K值为4.4 PC/N。

2 实验结果与讨论

由PVDF测得的典型002号和006号实验时间-电压信号如图4(a)和图5(a)所示，再由式(1)和式(2)即可得到相应的时间-应力信号(见图4(b)和图5(b))。

图4 002号试样时间-电压曲线及时间-应力曲线Fig. 4 Curves of time versus voltage andtime versus stress for sample 002

图5 006号试样时间-电压曲线及时间-应力曲线Fig. 5 Curves of time versus voltage andtime versus stress for sample 006

由G1和G2处的波形曲线得到试样中应力传播的时间为Δt，若试件厚度为h，则可计算冲击波速度

D=h/Δt

(3)

由冲击波波阵面关系[17]

[σ]=-ρ0D[u]

(4)

[u]=-D[ε]

(5)

对002号实验进行应变率估计，由图4(a) 时间-电压曲线可知，加载升压时间约为0.654×10-6s，由表3可知，根据实测数据估算的最大应变约为0.131 3，故应变率近似为2.01×105s-1，同样可得其余试样中的应变率。图4(b)、图5(b)的曲线显示，冲击波峰值随撞击速度的提高而增加，G1和G2处的应力在迅速上升至波峰后均随时间衰减；同时，冲击波峰值又随传播距离的增加而衰减，而且测点越往后，波形展宽且应力脉冲的升时也明显地增长，呈现出明显的黏性本构特性和冲击波由强间断波向弱间断波的逐渐转化的特征，这与张忠孝等对C40混凝土，王永刚等对C30混凝土平板撞击实验的观测结果相似。

由于水泥砂浆材料内部含有大量的微损伤缺陷，在冲击载荷作用下这些微缺陷引起了应力幅值的衰减，伴随着能量的耗散，反映了应力脉冲与材料细观结构相互作用的过程和结果。由此，可以更好地理解混凝土类多孔介质由于本构耗散引起的冲击波衰减现象。另外，随着冲击速度的增加，衰减效应更为明显。当撞击速度为257.07 m/s时(002号)，应力峰值由G1处的1.689 GPa降至G2处的1.116 GPa，衰减率为33.9%；当撞击速度为439.6 m/s时(006号), 应力峰值由G1处的2.371 GPa降至G2处的1.366 GPa，衰减率为42.4%。

表3 5个水泥砂浆试样实验结果

3 冲击绝热关系

由表3可确定砂浆试样的冲击波速度D与粒子速度u之间的冲击绝热关系，即D-u关系(见图6)。由图6可见，与大多数材料相同，水泥砂浆的D与u之间也存在线性关系，按线性公式

D=C0+qu

(6)

进行拟合，可得体积声速C0=1 838 m/s和斜率q=1.93。因而有

D=1 838+1.93u

(7)

图6 砂浆冲击波速度D与粒子速度u的Hugoniot曲线Fig. 6 The curve of shock wave speed and particle velocity for cement mortar

根据公式

ρ=ρ0D/(D-u)

(8)

可以得到P-ρ的Hugoniot关系，如图7所示，式(8)中：ρ为冲击状态的材料密度，ρ0为初始状态的材料密度。

对于多孔介质的理论密实密度ρgrain的计算，采用

图7 砂浆压力P与密度ρ的Hugoniot曲线Fig. 7 The curve of shock wave pressure and density for cement mortar

了传统的Hugoniot混合法。根据干燥水泥砂浆试样各组分的质量分数mi和ρi，可预测材料理论密实密度

(9)

式中：水泥砂浆各组分参数如表4所示。

表4 水泥砂浆试样组分及质量分数

需要指出的是，PHEL值的大小依赖于拟合的函数形式，但主要还是取决于材料组分、密度和强度。Gebbeken等取PHEL= 0.6 GPa，Grady[18]取PHEL=0.5 GPa，Gebbeken等[19]取PHEL= 0.25 GPa。同样，Cpor和Cgrain的值，也是由材料本身的构造所决定的。计算结果表明，密实材料波速大于初始弹性波速，主要原因是在水泥砂浆中，存在相当数量的初始微缺陷，包括微裂纹和微孔洞，使得冲击波的能量很大程度上耗散在微缺陷变形与压溃，进而影响了冲击波的传播，当压力较高时，材料由初始的含孔隙状态转变成相对致密的状态，使得密实材料波速有着显著的提高。

4 状态方程

为实现不同压力水平下含孔隙的水泥砂浆物态变化的完整描述，将低压段的孔隙压密P-α状态方程和高压段的Mie-Grüneisen型状态方程相连接。如图8所示，随着压力增加，P-α曲线依次经历弹性区(Ⅰ区，αp<α<α0，骨架的弹性变形，可恢复)，孔隙压密区(Ⅱ区，1≤α<αp，孔隙坍塌)和基体压缩区(Ⅲ区，无孔隙的基体材料压缩)。α的定义式为

(10)

图8 多孔材料状态方程曲线Fig. 8 Schematic of the postulated compaction behavior of a porous material

式中：ρ和ρs分别为孔隙介质和基体的密度。

由于弹性区孔隙率变化很小，假设在弹性区满足dα/dP=0，忽略弹性阶段孔隙率的微弱影响，则原始P-α模型[20]简化成图9所示，此时水泥砂浆材料孔隙压实过程由式(11) 描述。

图9 简化后的P-α状态方程曲线Fig. 9. The curve of modified P-α equation of state

(11)

式中：Pe为对应孔隙开始坍塌时的压力；Ps为孔隙恰好完全消失时的压力；n为压缩指数；α0为初始孔隙率参数。

密实的砂浆材料体积容变律采用多项式形式的Mie-Grüneisen型状态方程，并引入参数α，其方程具体形式为

(12)

(13)

为了确定低压到高压段完整的状态方程，仍需要确定参数Pe，Ps，n及K1，K2，K3的值。Pe=PHEL=0.25 GPa；由图7可知，当压力P由2.29 GPa上升到2.37 GPa时，材料密度(或体变)几乎不再变化，类似锁变现象，体变μs=0.08，取Ps=2.29 GPa；对于水泥砂浆材料，取n=3[21]。K1=E/[3(1-2ν)][22]，泊松比ν=0.2[23]，杨氏模量E=11 700(fc)0.3，fc=41.8 MPa为砂浆的单轴压缩强度，由此算得K1= 20 GPa，由于缺少更高压力下密实砂浆材料的压力与体变数据，考虑到密实的混凝土类材料的压缩行为基本相似[24]，本文取K2=30 GPa，K3=10 GPa。具体模型及参数详见表5。

表5 水泥砂浆状态方程及参数

5 结 论

本文对水泥砂浆试样进行了一维应变动态力学行为的实验研究，通过对实验结果的讨论与分析，主要结论如下：

(1)时间-应力曲线表明，应力峰值随撞击速度的提高而增加，应力在迅速上升至波峰后随时间衰减，冲击波峰值随传播距离而衰减，冲击速度越高衰减效应越明显；测点越往后，波形展宽，应力脉冲升时也明显地增加。从细观角度探讨了应力脉冲与材料细观结构相互作用的过程和结果，揭示了混凝土类多孔介质产生冲击波衰减现象的物理本质。

(2)确定了材料的冲击绝热关系，其中冲击波速度D与粒子速度u之间满足线性关系，压力P与密度ρ的Hugoniot关系分为弹性段和压实段，基于拟合曲线计算了材料的Hugoniot弹性极限，初始弹性波速，密实材料波速，上述参数的取值依赖材料本身构造，如组分、密度、强度。

(3)将材料的孔隙压实和基体压实分别采用P-α状态方程和多项式形式Mie-Grüneisen型状态方程描述，给出了模型参数值。

参 考 文 献

[ 1 ] 张忠孝， 董海威， 陈江瑛， 等. 混凝土材料的平板撞击实验与数值模拟研究[J]. 宁波大学学报(理工版)， 2011， 24(3)： 80-85.

ZHANG Zhongxiao, DONG Haiwei, CHEN Jiangying, et al. Study on planar impact and numerical simulation for concrete materials[J]. Journal of Ningbo University ( Natural Science & Engineering), 2011, 24(3): 80-85.

[ 2 ] 王永刚， 王礼立. 平板撞击下C30混凝土中冲击波的传播特性[J]. 爆炸与冲击，2010， 30(2): 119-124.

WANG Yonggang, WANG Lili. Shock wave propagation characteristics in C30 concrete under plate impact loading[J]. Explosion and Shock Waves, 2010, 30(2): 119-124.

[ 3 ] 王永刚，张远平，王礼立. C30混凝土冲击绝热关系和Grüneisen型状态方程的实验研究[J]. 物理学报， 2008， 57(12): 7789-7793.

WANG Yonggang, ZHANG Yuanping, WANG Lili. Experimental study on the shock Hugoniot relationship and the Grüneisen-type equation of state for C30 concrete[J]. Acta Physica Sinica, 2008, 57(12): 7789-7793.

[ 4 ] GEBBEKEN N, GREULICH S, PIETZSCH A. Hugoniot properties for concrete determined by full-scale detonation experiments and flyer-plate-impact tests[J]. International Journal of Impact Engineering, 2006, 32(12): 2017-2031.

[ 5 ] 严少华，钱七虎，周早生，等.高强混凝土及钢纤维高强混凝土高压状态方程的实验研究[J].解放军理工大学学报，2000，1(6)：49-53.

YAN Shaohua, QIAN Qihu, ZHOU Zaosheng, et al. Experimental study of equation of state for high-strength concrete and high-strength fiber concrete[J]. Journal of PLA University of Science and Technology, 2000, 1(6): 49-53.

[ 6 ] 蒋国平， 焦楚杰， 肖波齐. 高强混凝土气体炮试验与高压状态方程研究[J]. 物理学报， 2012， 61(2)： 354-358.

JIANG Guoping, JIAO Chujie, XIAO Boqi. High-pressure state equation of high strength concrete investigated with the gas gun experiment[J]. Acta Physica Sinica , 2012, 61(2): 354-358.

[ 7 ] 宁建国， 刘海峰， 商霖. 强冲击载荷作用下混凝土材料动态力学特性及本构模型[J]. 中国科学G辑(物理学 力学 天文学)， 2008， 38(6)： 759-772.

NING Jianguo, LIU Haifeng, SHANG Lin. The dynamic mechanical properties and constitutive model of concrete under intense dynamic loading[J]. Scientia Sinica Physica, Mechanica & Astronomica, 2008, 38(6): 759-772.

[ 8 ] LIU H F, FU J, NING J G. Experimental study on the dynamic mechanical properties of reinforced concrete under shock loading[J]. Acta Mechanica Solida Sinica, 2016, 29(1): 22-30.

[ 9 ] 施绍裘， 陈江瑛， 李大红， 等. 水泥砂浆石在准一维应变下的动态力学性能研究[J]. 爆炸与冲击， 2000， 20(4)： 326-332.

SHI Shaoqiu, CHEN Jiangying, LI Dahong, et al. A study on the dynamic mechanical behavior of cement mortar under quasi-one dimensional strain state[J]. Explosion and Shock Waves, 2000, 20(4): 326-332.

[10] 施绍裘， 王礼立. 水泥砂浆石在一维与准一维应变状态下动态力学响应的比较和讨论[J]. 岩石力学与工程学报， 2001， 20(3)： 327-331.

SHI Shaoqiu, WANG Lili. Discussion on dynamic mechanical behaviors of cement mortar under quasi-one and one dimensional strain states[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(3): 327-331.

[11] WANG L L, SHI S Q, CHEN J Y, et al. Influences of strain-rate and stress-state on dynamic response of cement mortar[J]. International Journal of Structure Stability and Dynamics, 2003, 3(3): 419-433.

[12] GROTE D L, PARK S W, ZHOU M. Dynamic behavior of concrete at high strain rates and pressures: experimental characterization[J]. International Journal of Impact Engineering, 2001, 25(9): 869-886.

[13] TSEMBELIS K, PROUD W G, FIELD J E. The dynamic strength of cement paste under shock compression [C]∥ AIP Conference Proceedings, CP620, Shock Compression of Condensed Matter. New York: American Institute of Physics， 2001.

[14] RIEDEL W, WICKLEIN M, THOMA K. Shock properties of conventional and high strength concrete: experimental and mesomechanical analysis[J]. International Journal of Impact Engineering, 2008, 35(3): 155-171.

[15] 李焰， 张向荣， 谭红梅， 等. 国产 PVDF 压电薄膜的冲击加载及卸载响应研究[J].高压物理学报， 2004， 18(3)： 261-266.

LI Yan, ZHANG Xiangrong, TAN Hongmei, et al. Response of homemade PVDF piezofilm under shock loading and unloading[J]. Chinese Journal of High Pressure Physics, 2004, 18(3): 261-266.

[16] 王礼立. 应力波基础[M]. 北京： 国防工业出版社，2005.

[17] 马晓青. 冲击动力学[M]. 北京： 北京理工大学出版社，1992.

[18] GRADY D E. Impact compression properties of concrete[C]∥Proceeding of the 6th International Symposium on Interaction of Nonnuclear Munitions with Structures. Panama: University of California Press, 1993.

[19] GEBBEKEN N, RUPPERT M. A new concrete material model for high dynamic hydrocode simulations[J]. Archive of Applied Mechanics, 2000, 70(7): 463-478.

[20] HERRMANN W. Constitutive equation for the dynamic compaction of ductile porous materials[J]. Journal of Applied Physics, 1969, 40(6): 2490-2499.

[21] HARTMANN T, PIETZSCH A, GEBBEKEN N. A hydrocode material model for concrete[J]. International Journal of Protective Structures, 2010, 1(4): 443-468.

[22] XU H, WEN H M. A computational constitutive model for concrete subjected to dynamic loadings[J]. International Journal of Impact Engineering, 2016, 91: 116-125.

[23] POLANCO-LORIA M, HOPPERSTAD O S, BØRVIK T, et al. Numerical predictions of ballistic limits for concrete slabs using a modified version of the HJC concrete model[J]. International Journal of Impact Engineering, 2008, 35(5): 290-303.

[24] HOLMQUIST T J, JOHNSON G R, COOK W H. A computational constitutive model for concrete subjected to large strains, high strain rates, and high pressures[C]∥Proceeding of 14th International Symposium on Ballistics. Quebec: DEStech Publications, 1993.