道面脱空检测中Rayleigh波频散曲线的提取

，，， ，，

(南京航空航天大学 自动化学院， 南京 211106)

瑞利波于1885年由英国物理学家Rayleigh首先发现并证明[1]，其是在以真空或气体为界的自由固体表面上传播的弹性表面波[2]。瑞利波具有低频、低速、强振幅的特点，振幅随着波的传播深度的增大呈指数迅速衰减[3]，在层状介质中具有频散特性，即波速随波长的变化而变化[4]。瑞利波检测正是利用这些特性，在地质勘探、无损检测等领域被广泛应用。目前国内外有三种主要的瑞利波地质勘探法，分别是微动法、稳态法和瞬态法[5]。

地质勘探中，携带了地下不同深度处介质信息的瑞利波的频散特性可以帮助人们探测地下介质结构。因此，如何准确可靠地提取频散曲线是瑞利波勘探技术的关键问题之一。为此，前人做了大量研究，其中TATHAM[6]等人提出利用τ-p变换进行波场分离的思想；陈淑珍，刘怀林[7]证实了τ-p变换法求瞬态瑞利波的频散曲线具有失真小等特点；刘云祯[8]等通过多道分析选择最佳观测时窗，利用f-k变换法提取瑞利波频散曲线，具有运算简便、易于实现的特点。

笔者首先通过理论研究，对τ-p变换法和f-k变换法在瑞利波数据处理中的应用做了分析；然后针对道面脱空检测设计了试验，分别使用τ-p变换法和f-k变换法对试验数据进行处理，提取出频散曲线，并对两种变换法的处理效果进行对比。

1 瑞利波频散曲线及其提取

1.1 频散曲线及其提取方法

频散曲线指的是频散波的频率与波速间的对应关系曲线。瑞利波在不均匀的介质中传播时会发生频散现象，即传播速度与传播介质的物理性质相关。常用的瑞利波频散曲线提取方法有f-k变换法以及τ-p变换法[9]。

1.2 频散曲线提取的τ-p变换法

1.2.1τ-p变换原理

τ-p变换是将t-x域的信号变换到截距(τ)斜率(p)域的变换方法。瑞利波和其他的规则波具有不同的视速度v*(即p值不同，p=1/v*),所以其处于不同的p值区间。因此，将数据经τ-p变换后，再滤掉噪声保留瑞利波，然后反变换回t-x域，这样就提纯了瑞利波。由t-x域变换到τ-p域，从数学上相当于做了一次坐标变换

t=τ+px

(1)

式中：t为波的传播时间；x为波在水平方向的传播距离。

对瑞利波而言，其时距曲线方程如下式

t=x/νR

(2)

p=dt/dx=1/νR

(3)

式中:νR为瑞利波的相速度。

因此，在t-x域内为直线的瑞利波，在τ-p域内变为一个点。同理，在t-x域内为直线的直达波、折射波在τ-p域内也为一个点，但p值不相同。对于反射波而言，其时距曲线方程为

(4)

式中：h为波在竖直方向的传播深度。

则

(5)

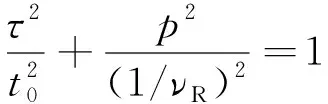
(6)

式中：k为波数。

可见在t-x域内为双曲线的反射波，在τ-p域内变为椭圆。瑞利波、直达波和声波都从震源出发，其时距曲线在t轴的截距为零，因此，其都在τ=0的p轴上。由于直达波时距曲线在无限远处与同一界面的反射波时距曲线相切，即在该处具有相同的p值，所以直达波与反射波在p轴上共点。而瑞利波时距曲线因斜率大于直达波时距曲线，故p值大，它的点位于椭圆之外。折射波时距曲线由于与同一界面的反射波时距曲线相切，它的点位于椭圆上与临界角对应的p值处。

τ-p变换的实现归结于倾斜叠加，在t-x域中的信号φ(t,x)经过τ-p变换后的输出φ(τ,p)为：

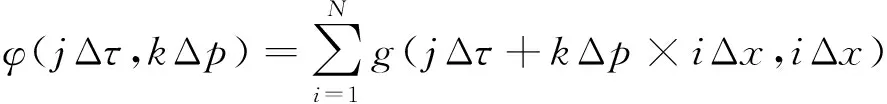
(7)

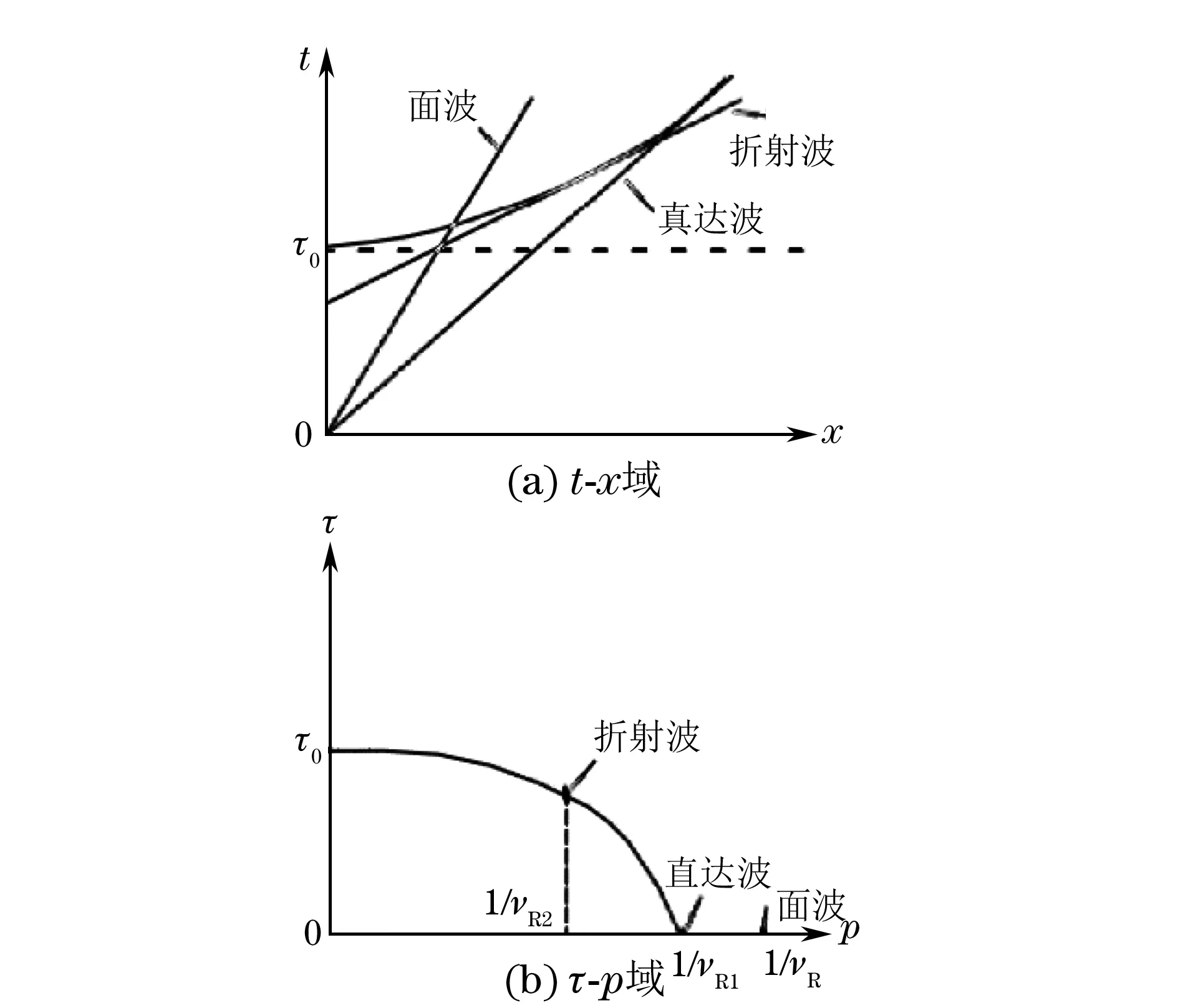
图1 t-x域和τ-p域各个位置的示意

1.2.2 利用τ-p变换提取频散曲线的步骤

(1) 将数据信号记录的(t,x)域，利用τ-p变换可以变成(τ,p)域。

(2) 对(τ,p)域记录的每一个p道进行一维傅里叶变换可以得到f-p域记录。

(3) 令νRi=1/pi，可以得到f-νR域记录。

(4) 取f-νR域记录中的极值点可以得到(fi,νRi)，将其连成线就得到了f-νR曲线。

(5)Hi=νRi/(2fi)，将(Hi,νRi)点连成线就可得到速度关于半波长的曲线。

1.3 频散曲线提取的f-k变换法

1.3.1 瑞利波信号增强

虽然瑞利波在地震波中具有能量高的特点，但要满足检测需求，还须进行信号增强，提高信噪比。由于瑞利波的面波特点，瑞利波能量主要聚集于自由表面，也就是地表浅表面。由于其强度在竖直深度方向呈指数递减，所以可增大深层信号的放大倍数，减小浅地表信号的放大倍数。

1.3.2f-k滤波

f-k滤波是根据f-k变换法的二维傅里叶变换原理来实现的。将波的传播时间t及空间距离x表示的函数f(t,x)中的一个记录d(t,x)沿t轴做傅里叶变换，将t-x域信号变换到f-x域，然后对得到的D(f,x)信号沿x轴做傅里叶变换，转换为以频率f和波数k所表示的函数F(f,k),如下式所示。

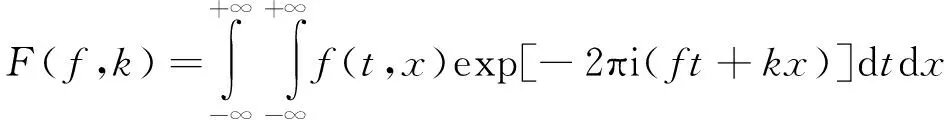
(8)

图2 频率波数谱F的示意

图2为频率波数谱F的示意图。由图2可发现，通过原点的直线上的每一个f/k都是一个常数，这说明在t-x域上该直线就是一个确定的速度。利用这一性质，可在频率波数谱上设计一个滤波器,表示为

(9)

式中：D集合为图2中标出的有效信号区和规则干扰区。

因此可得

F(f,k)×H(f,k)=F′(f,k)

(10)

至此，滤波工作完成。

1.3.3 二维傅里叶变换

瑞利波数据的时间-空间域可看作为时间t和空间距离x的二维函数f(x,t)，在道面脱空检测中，需在道面上铺设若干道传感器节点，在道数N和每道的采集点数M已经确定之后，则得到下式。

f(m,n)=f(x0+mΔx,t+nΔt)

(11)

式中：m=0,1,…，N-1;n=0,1,…，M-1;Δx为道间距；Δt为采样间隔。

对f(m,n)作二维傅里叶变换

(12)

式中：W=e-2π;f为频率，f=0,1,…,M-1;k为波数,k=0,1,…,N-1。

由于经过傅里叶变换和滤波后的函数F(f,k)具有对称性，因此得到的(N/2,M/2)是一系列对称的点，同时F(f,k)和F(N-k,M-f)为一对共轭复数，它们所对应的是同一波谱。因此只需要对(0～N/2,0～M/2)的1/4区域分析就能够得到全波谱的信息。因为在地震波中，瑞利波所占的能量比重很高，达到67%[10]，故通过F(k,f)振幅能量谱，标出能量最大线上的各点，再根据半波长理论就可以绘制瑞利波的频散曲线。

1.3.4 频散曲线的获得

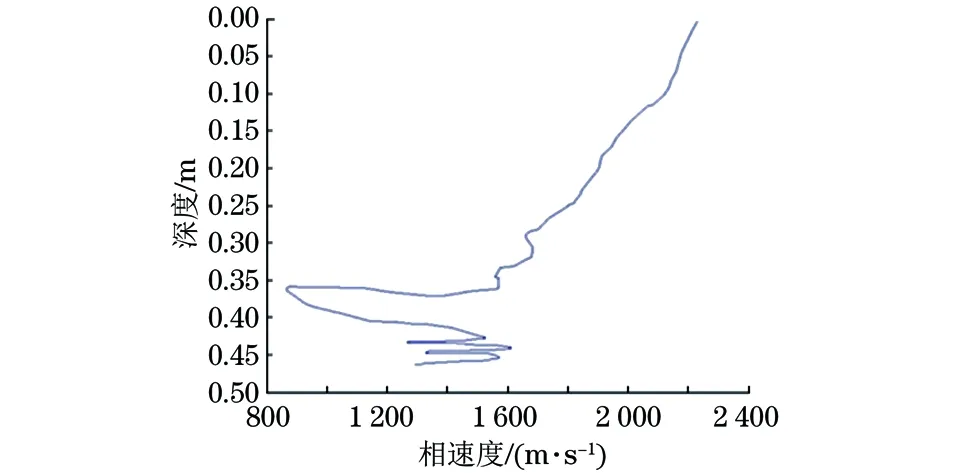
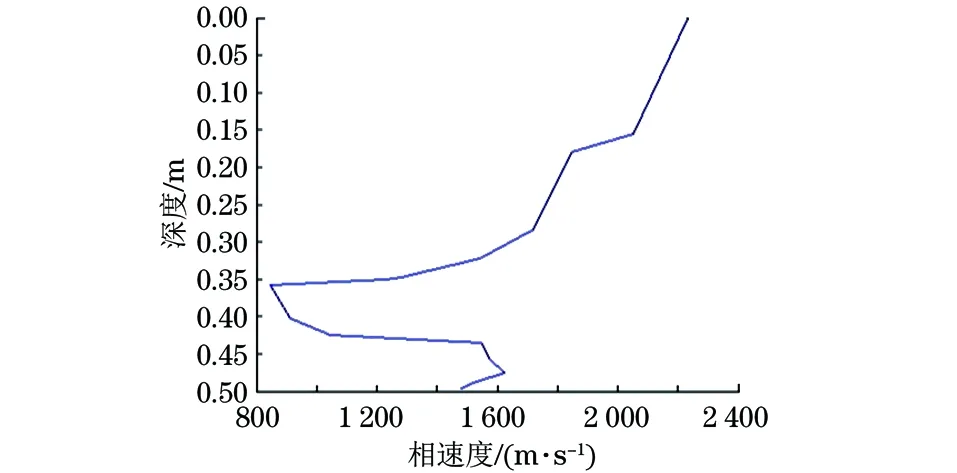
取频率-波数(f-k)能量谱中值最大的一点ki(0≤ki

则得到，在能量谱上的ki点处的相速度与波长的关系为

(13)

λRi=N·Δt/ki

(14)

依据半波长理论，可得

(15)

根据式(14)可得到瑞利波的频散曲线。

由于τ-p变换是线性变换，具有良好的保真性，可以将反射波和折射波进行有机结合，将无用的噪声波也作为利于检测的波形；f-k变换解决了一维数字处理技术存在的不足，同时充分利用了多道瞬态瑞利波数据信息的优势。

但τ-p变换算法是通过对原信号进行采样、求导后取得的，因此也存在一些弊端，如会出现假频现象和端点效应[11]。这对道面检测中频散曲线反映出的地下脱空结果的准确性会造成影响，所以τ-p变换需要经过一定的优化才能够获得较为准确的结果。加之，考虑到程序设计的复杂性，认为f-k变换更加符合检测需求，因此在道面检测中更适合用f-k变换法来提取频散曲线。

2 模拟道面脱空检测试验及频散曲线提取

2.1 试验方案

文章通过以下的道面脱空检测模拟试验来验证频散曲线提取的理论分析结果。

试验对象为带有圆形空洞的混凝土板(长×宽×高为1 750 mm×1 500 mm×80 mm)，空洞圆心位置距离上表面深度约350 mm，震源采用锤击生成瑞利波，试验装置布置示意及混凝土板实物如图3所示。

采用3道加速度传感器采集信号，每道采集1 024个点，采集频率为1 000 Hz，道间距为100 mm，布线采用线性等间距排列方式；用激励锤正面垂直敲击水泥板。每个测试点均分别采用100，200mm偏移距做了测试，每个激发点进行数次激发，选取瑞利波能量强、干扰小、信噪比高的记录作为瑞利波数据并加以处理。

图3 脱空检测模拟试验装置布置示意及混凝土板实物

2.2 试验结果

首先使用τ-p变换法对获得的数据进行处理，提取出的频散曲线如图4所示。

图4 采用τ-p变换获得的频散曲线

从图4中可看出，频散曲线在0.35～0.40 m的深度处出现了明显的频散曲线的突变——波速瞬间下降后回折。这说明瑞利波传播经过的介质的性质发生了改变——即混凝土板上设置的空洞。该曲线整体特征鲜明，反映出了样本的特征。

然后采用f-k变换法对该试验数据进行处理，提取出的频散曲线如图5所示。

图5 采用f-k变换获得的频散曲线

从特征上看，该曲线上的突变位置与τ-p变换法所得曲线上的突变位置比较，相差不大，但由于弱化了其他的突变曲线，使得空洞造成的频散曲线特征更加突出，从而更加利于对样本空洞属性的分析，因此针对道面检测，选用f-k变换法来提取频散曲线更合适。

3 结语

通过阐述τ-p变换法和f-k变换法的原理与步骤，对两种方法在瑞利波数据处理中的应用特点做了对比，得出道面脱空检测中f-k变换法提取频散曲线要优于τ-p变换法的结论；然后设计了模拟道面脱空检测试验，分别使用τ-p变换法和f-k变换法对混凝土构件模型测试波形数据进行处理，提取出频散曲线，验证了f-k变换法在道面检测提取瞬态瑞利波频散曲线中的效果更好。实际检测中，当各种转换波与面波严重耦合在一起时，f-k变换法也存在难以选择最佳观测窗口的问题，要想改进f-k变换法尚需要进一步的深入研究。

参考文献:

[1] LORD R. On waves propagated along the plane surface of an elastic solid[J].Proceedings of the London Mathematical Society,1885,1(1):4-11.

[2] 张波，李健君.瑞利波反射理论探讨[J].无损检测，2001,23(11):472-478.

[3] 辛小春.面波新技术在工程地质勘察场地评价中的应用[J].北京水利,2003(1):25-26.

[4] 杨成林.瑞利波勘探[M].北京：地质出版社, 1993.

[5] 严寿民.瑞利波勘探方法的应用与展望[J].地球物理学进展,1991(2):21-30.

[6] TATHAM R H, GOOLSBEE D V. Separation of S-wave and P-wave reflections offshore western Florida[J]. Geophysics, 1984,49(5):493-508.

[7] 陈淑珍，刘怀林.基于τ-P变换技术实现多波波场分离[J].煤田地质与勘探，1998,22(5):336-376.

[8] 刘云祯，王振东.瞬态面波法的数据采集处理系统及应用实例[J].物探与化探,1996,20(1):28-33.

[9] 张碧星，鲁来玉，鲍光淑.瑞利波勘探中“之”字形频散曲线研究[J].地球物理学报2002,45(2):263-274.

[10] 刘强.基于瑞利波理论的公路无损检测方法研究[D].西安:长安大学,2010.

[11] 宋先海，肖柏勋，张学强,等.用改进的τ-p变换算法提取瞬态瑞利波频散曲线[J].物探与化探,2003,27(4):292-295.