无人机质量特性参数一体化测量系统的研究

温晶晶, 邓 聃, 吴 斌

(1. 西北工业大学 航天学院, 陕西 西安 710072; 2. 四川航天系统工程研究所, 四川 成都 610100)

1 引 言

质量特性参数(质量、质心、转动惯量和惯性积)是飞行器总体设计的重要参数[1-3],在工程实际中,经常需要对其进行测量。目前,常用的质量特性测量设备主要存在以下问题:(1)主要用于测量导弹、火箭等回转体飞行器,尚未发现成熟的测量无人机这类非回转体的质量特性参数的设备[4～6];(2)一台设备通常不能测量出全部的质量特性参数,且被测物需要多次装夹,操作过程繁琐[5,7]; (3)在测量俯仰和滚转方向转动惯量时,传统的竖直安装测量法容易对无人机等薄壁结构造成损害,并且也可能造成设备掉落而出现安全事故。

针对上述问题,本文设计了一套全新的无人机质量特性参数一体化综合测试系统,通过一次装夹即可测量出无人机的全部质量特性参数,操作效率高。针对竖直安装测量法带来的安全性和稳定性问题,本文提出了小角度翻转测量法。试验表明,该方法既满足测量准确度又保证了产品测量的安全性;实际使用过程中,该系统也取得了良好效果。

2 测量台的设计

测量台主要由底座组件、翻转机构、转盘机构、工作平台及工装夹具等组成,如图1所示。其中底座组件和转盘机构是整个测量台的核心。

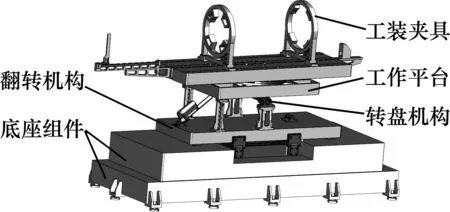
图1 测量台三维示意图

底座内有3个称重传感器,用于质量质心的测量;预扭电机用于推动扭摆台体转动,达到预定扭转角度后,预扭释放机构自动释放,扭摆台体在扭杆作用下来回摆动,从而可以测量转动惯量和惯性积;底座下面安装有调平机构,工作平台上安装有精密水平仪,进而实现测量平台的精确调平;固定在底座上的升降机构和升降电机可以控制测量平台的升降;转换机构用于质量质心和转动惯量及惯性积测量功能的转换。详细的底座组件示意图如图2所示。

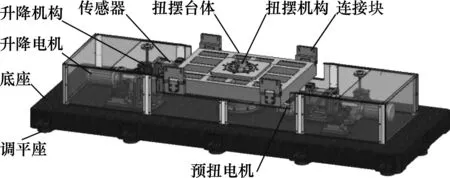
图2 底座组件示意图

翻转机构通过电动缸的直线伸缩运动实现翻转;转盘机构上设计有8个不同的分布角度的定位锁紧链接孔(0°,45°,90°,135°,180°,225°,270°和315°),用于工作平台偏航方向旋转时的角度定位和锁紧(用定位锁紧销锁紧)。通过翻转机构和转盘机构的相互配合,可以实现测量台不同测量状态的转换。

3 质量质心测量

质量质心的测量方法主要有机械重定位法、不平衡力矩法和多支点称重法等[8,9],本文中采用多支点称重法。多支点称重法可同时测量出产品的质量和质心,结构简单,对测量环境和设备调平都没有较高要求。

称重传感器在测试平台上的投影如图3所示。其中点1,2,3分别表示3个传感器和测量平台的接触点;OX、OZ为装置参考轴;原点O为测量平台的定位中心;H2,H3,L1,L2,L3分别为3个称重传感器与参考轴OX,OZ的垂直距离。设Oxyz为机体坐标系,测量平台的OX轴和机体Ox轴重合,点C为试件质心在XOZ平面的位置,有:

G=G1+G2+G3

(1)

式中:G为被测物重量;G1,G2,G3分别为传感器1,2,3的实测值。

图3 传感器安装示意图

各点的分重量测出后,根据力矩平衡原理在平面XOZ内对OZ取矩可得被测物在OXZ平面内的轴向质偏Xc为:

(2)

对OX取矩可得横向质偏Zc为:

(3)

通过上述步骤已经测得被测物x向和z向质心,然后将测量平台绕OZ轴翻转θ角,可以求得高度方向质偏Yc,图4为高度方向质偏测量原理图。

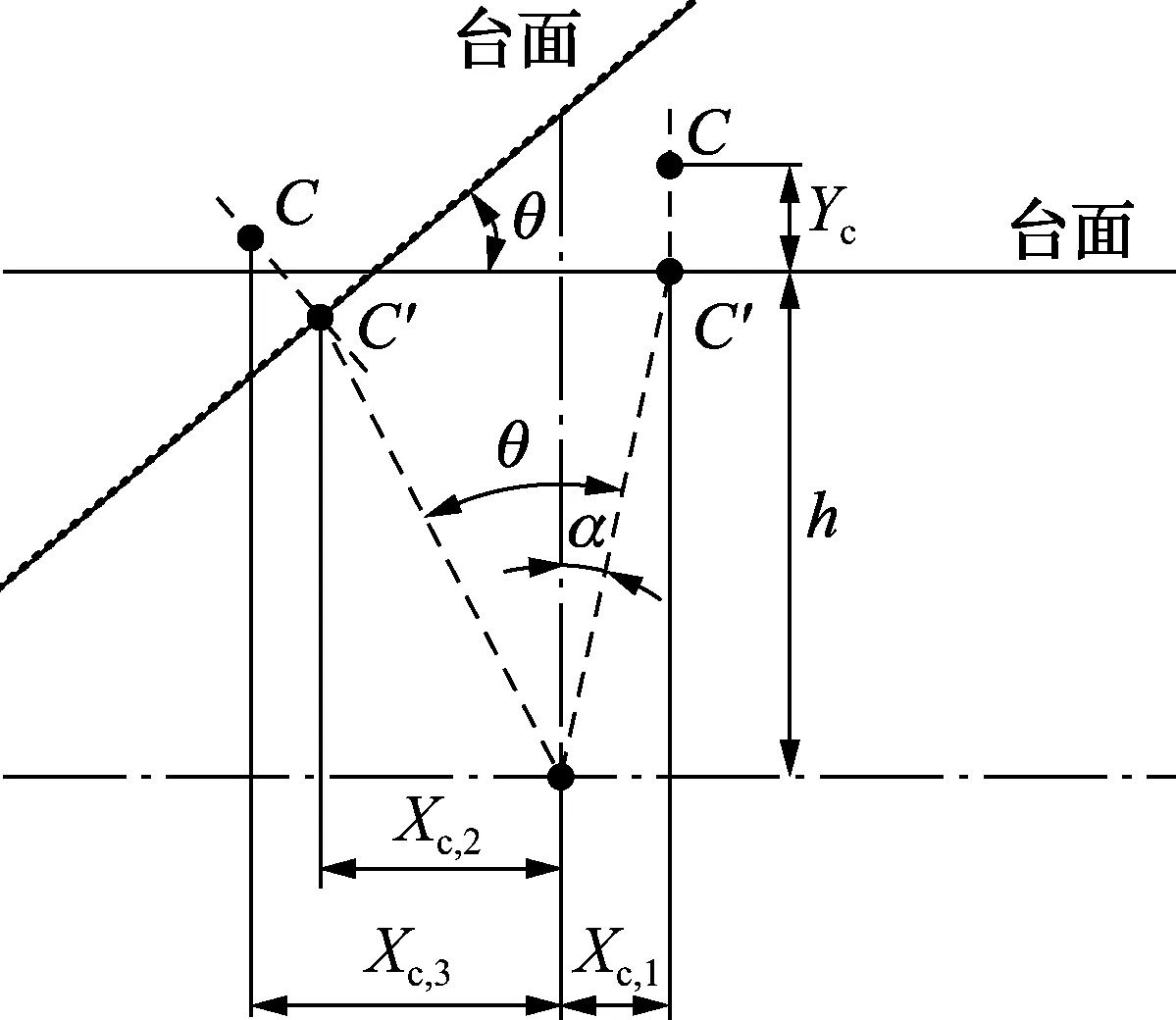
图4 高度方向质偏测量原理图

图4中C′为质心在台面的投影;h为台面到定位中心O的距离;Xc,1为水平测量时质心位置;Xc,2为翻转θ角后质心在台面上的投影点的位置;Xc,3为翻转θ角后质心位置。由几何关系有:

(4)

(5)

(6)

最后可以得到Yc的计算公式为:

(7)

X向质心是指产品质心到其尾部的距离;Y向、Z向质偏是产品质心相对于其几何轴线的偏移距离。

4 转动惯量和惯性积的测量

4.1 单轴转动惯量的测量

无人机质量特性参数测量系统采用扭摆法进行单轴转动惯量的测量。扭摆法是通过光电传感器测量摆动周期,计算出被测物的绕单轴的转动惯量[10]。扭摆系统如图5所示,考虑粘性阻尼,有:

(8)

式中:I为试件对H轴的转动惯量;K为扭杆刚度系数;ξ为系统粘性阻尼系数;T为系统自由扭摆周期。则系统的转动惯量为:

图5 扭摆系统示意图

先测得测试台的摆动周期为T0,然后把被测物装夹到测试台得摆动周期为TX。实际工程中认为2种状态下系统的粘性阻尼系数不变,则得到被测物的转动惯量IP为:

(10)

4.2 惯性矩和惯性积的求解

采用扭摆法和惯性椭球法相结合的方法来求解惯性矩和惯性积[11]。

如图6所示,以台面定位中心O为坐标原点建立右手坐标系OXYZ,OH轴为扭杆转轴。则被测物绕OH轴的转动惯量为:

IH=IXXcos2α+IYYcos2β+IZZcos2γ-

2IXYcosαcosβ-2IYZcosβcosγ-

2IXZcosαcosγ

(11)

其中:IXX,IYY,IZZ,IXY,IYZ,IXZ分别为被测物相对于坐标系OXYZ的3个转动惯量和3个惯性积;α,β,γ分别为待测物坐标系3个坐标轴与扭杆转轴的夹角,因此若测得6个不同状态下的转动惯量IH,就可以求得被测物相对于质心坐标系OXYZ的转动惯量和惯性积。

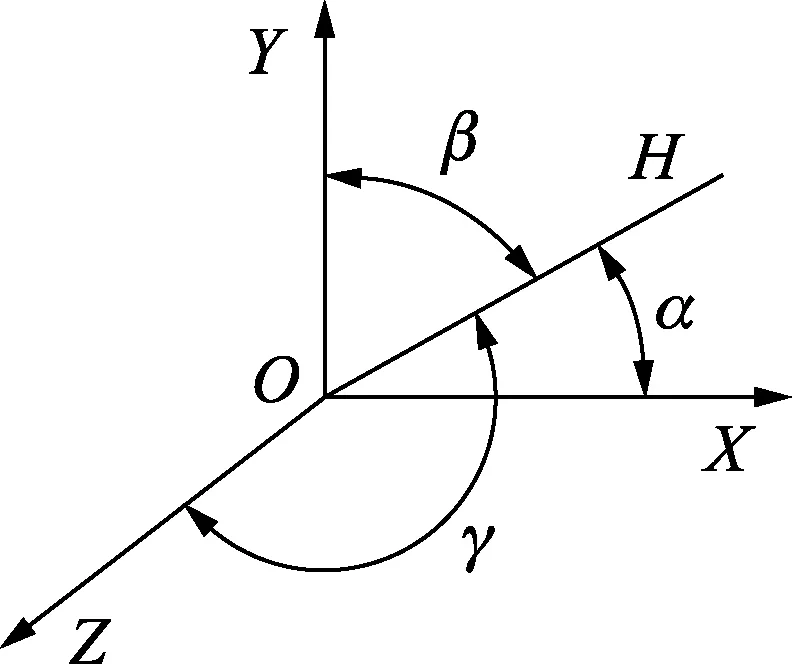
图6 质心坐标系的坐标轴与转轴OH的夹角

设6种状态下的试件绕OH轴的转动惯量测量值分别为IH1～IH6,各测量状态示意如图7所示。

图7 6种测量状态示意图

测量状态的参数如表1所示。通常在测量滚转方向和俯仰方向转动惯量时,总是要把产品竖直装夹,这样虽然测量准确度较高,但存在以下问题:

(1)装夹过程繁琐复杂;

(2)若试验室空间较小无法完成测量;

(3)为克服待测物自身重力,工装必须对待测物夹持较紧,这容易对无人机等薄壁结构设备造成损坏;

(4)容易造成设备掉落而出现安全事故。所以采取翻转小角度θ的方法来测量。

表1 测量转动惯量所选取的6种状态

代入公式(11)化简得:

(12)

解得6个惯性张量的值分别为:

(13)

5 翻转角度θ的选定

在测试时,首先需要加载标准件(即已知质量特性参数的样件)来标定测量台的测量参数,包括h,θ,Keq等。标定完成之后,就可以装夹产品进行测量。再由平行移轴定理,消除转动惯量测量时的被测物质心相对于测量轴OH的偏移di(i=1,2,…,6)引起的误差。

在消除质心偏移误差之后,根据误差传递理论[12～15]求得惯性积的极限误差表达式为:

(14)

(15)

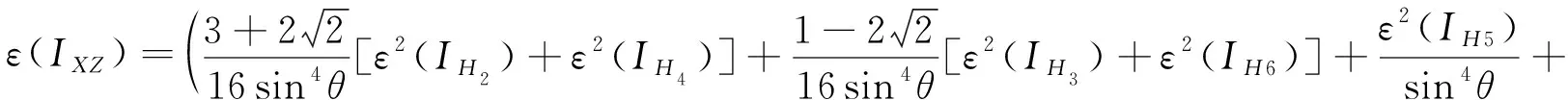
(16)

已知一钢制试件惯性张量的理论值如表2。

表2 试件惯性积张量的理论值 kg·m2

已知转动惯量IH1～IH6的测试准确度为0.1%,翻转角θ的极限误差为ε(θ)=20",取θ=30°,由式(12)计算得IH1～IH6的理论值和绝对误差如表3所示。

表3 IH1～IH6的理论值和绝对误差 kg·m2

将数据代入式(14)、式(15)和式(1)得惯性积的绝对误差和相对误差如表4所示。

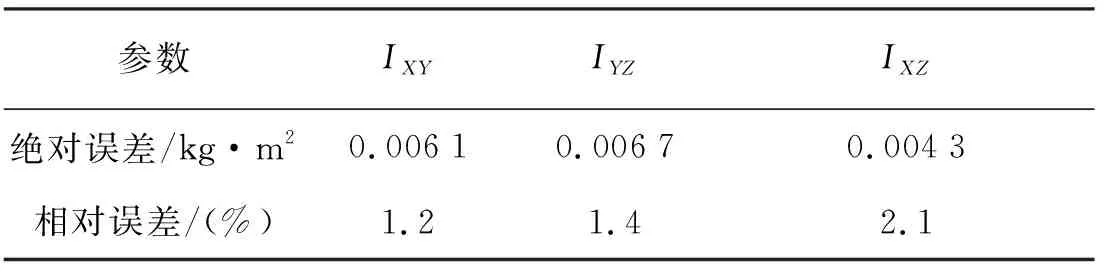
表4 惯性积的绝对误差和相对误差

图8给出了翻转角θ在20°～80°范围内变化时,惯性积测量的相对误差随其变化的规律。

图8 惯性积测量的相对误差和翻转角的关系

6 样件测试

为了验证系统的可靠性,用已知全部惯性张量的钢制样件进行测量。样件三维模型如图9所示,样件现场测量如图10所示。

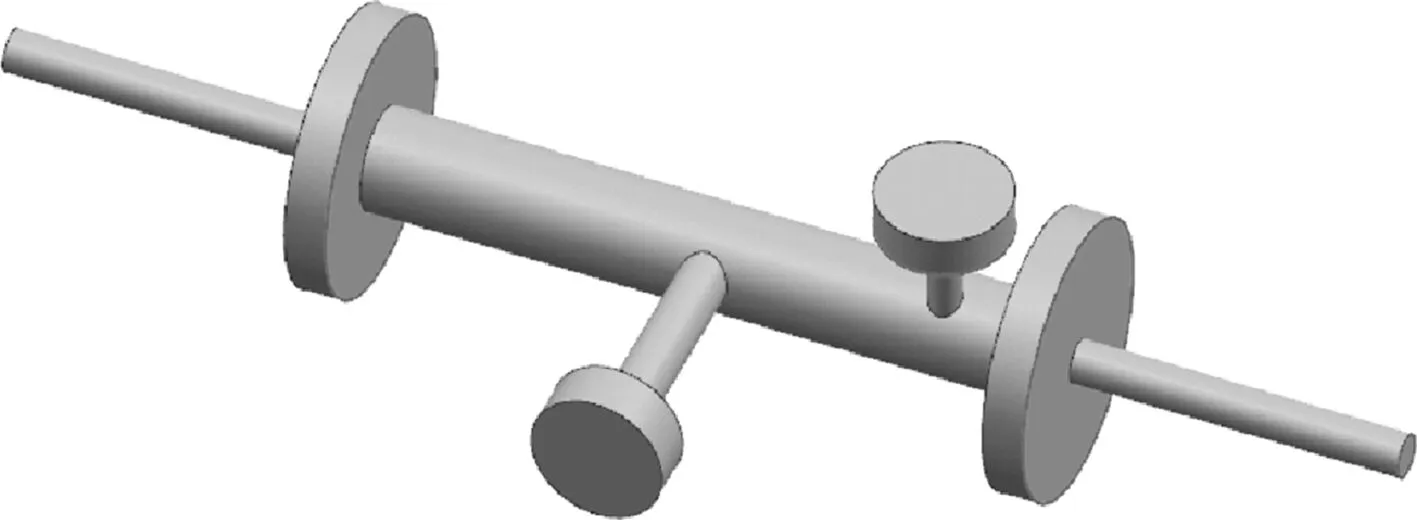
图9 样件三维模型图

图10 样件现场测试图

实际测试表明:质量质心测量相对误差和转动惯量测量相对误差均容易达到设计要求,而惯性积测量误差较难控制,受翻转角θ影响较大。分析图8可知,在20°～60°范围内,惯性积的相对误差随翻转角θ增大而减少。但为确保测量过程的安全性和稳定性,θ角越小越好。设计指标要求惯性积测量相对误差小于4%。本文从20°开始,以0.5°为步长,经过反复试验,最终取定翻转角θ=27.5°。

具体测试步骤及结果为:

(1)利用状态1可以测量出样件的质量和X向、Z向质心。然后转换到状态2,结合状态1测量出的纵向质心,表5列出了计算所需参数;

(2)将表5中数据代入式(1)～式(3)、式(7)计算得到质量质心测量值和仿真值的比较如表6所示;

表5 状态1和状态2测量参数

表6 样件质量质心测量值和仿真值比较

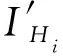
(4)将表7中数据带入式(13)计算得到转动惯量和惯性积的测量值如表8所示。

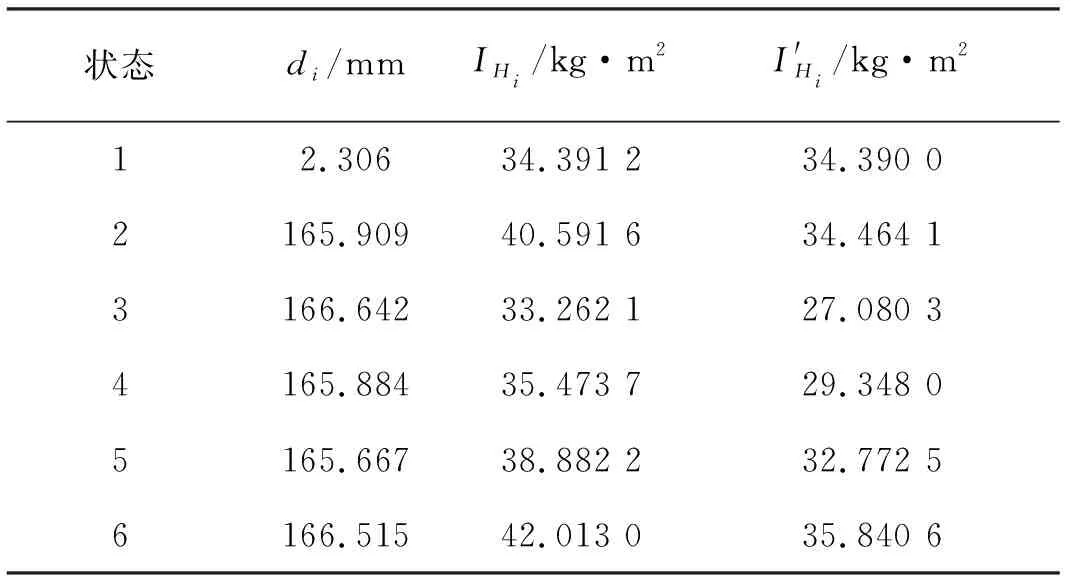
表7 转动惯量和惯性积计算参数

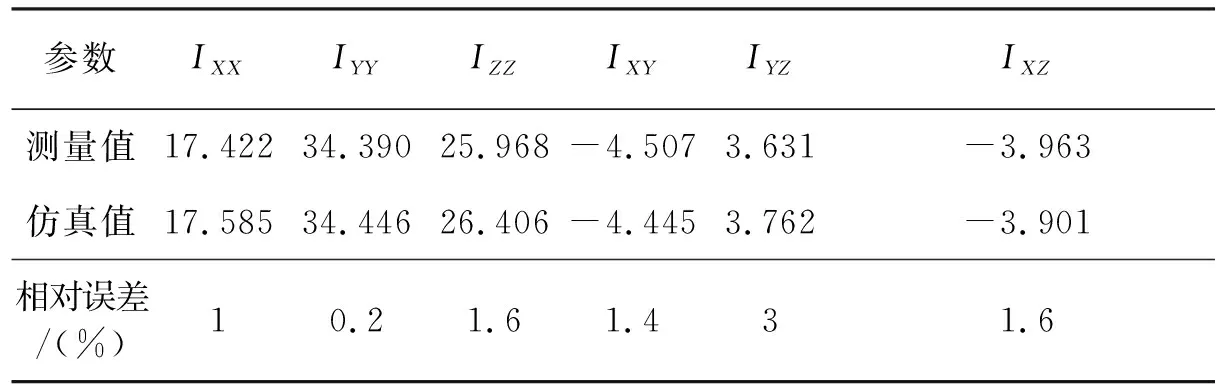
表8 样件惯性参数测量值和仿真值比较 kg·m2

通过测量值与仿真值的对比可以得出结论:质量测量相对误差小于0.02%;质心质偏测量相对误差小于1%;转动惯量测量相对误差小于2%;惯性积测量相对误差小于3%。以上指标不仅满足了设计要求,并且和以往同类型设备相比有很大改进。

7 结 论

(1)设计了一套无人机质量特性参数一体化综合测量系统；该系统通过一次装夹可测量出产品的全部质量特性参数,使得测量效率极大提升。

(2)系统采用小角度翻转测量法,解决了传统竖直测量方法带来的安全性和稳定性问题;且该系统已经投入使用,取得了良好的效果；同时该系统也可用于其它产品的测量。

(3)为了减小转动惯量和惯性积的测量误差,可以增加测量状态,按照第4.2节进行多于6次测量,再由最小二乘法得到最优解。但这会增大测量时间,在实际测量中要酌情考虑。

[参考文献]

[1] 陈平, 邓高福, 吴海瀛.飞行器模型质量特性参数一体化测量装置研究[J]. 机械科学与技术, 2015, 34(12):1891-1895.

[2] 王超,张晓琳,唐文彦,等.质量特性测量系统的运动学标定[J].计量学报,2014,35(6):595-598.

[3] 王超, 唐文彦, 张晓琳, 等. 大尺寸非回转体质量特性一体化测量系统的设计[J]. 仪器仪表学报, 2012, 33(7):1634-1639.

[4] 张俐,江春. 基于纵向对称面重合的机身位姿求解方法[J]. 计量学报. 2017,38 (4): 385-390.

[5] 王国刚, 刘玉宝, 刘强, 等. 一种测量无人机重心和转动惯量的方法[J]. 航空兵器, 2013, (5):7-11.

[6] 王瑾，孙宁. 基于转动惯量的刚体9个惯性参数的测量[J]. 计量学报, 2012,33(2): 135-139.

[7] 王超. 大尺寸飞行器质量特性测量关键技术研究[D]. 哈尔滨:哈尔滨工业大学, 2014:76-91.

[8] Boynton R, Wiener K. Mass properties measurement handbook[R]. SAWE Paper No.2444, Berlin,1998:17-49.

[9] Boynton R. Precise measurement of mass[J].SocAlliedWeightEngineers, 2001,8:1-30.

[10] Swank A J, Hardham C, Sun K X ,etal. Moment of inertia measurement using a five-wire torsion pendulum and optical sensing[J].AmericanSocietyforPrecisionEngineering, 2006:126-130.

[11] Zhao Y, Zhang X L, Wang J,etal. Measurement of Moment of Inertia Based on Torsion Pendulum[C]//International Conference on Advances in Mechanics Engineering, 2012, 964-967.

[12] 吴斌, 杨全洁. 用扭摆法测导弹惯性积的误差分析[J]. 弹箭与制导学报, 2005, 25(4):153-155.

[13] 费业泰. 误差理论与数据处理[M]. 5版. 北京:机械工业出版社,2005:52-97.

[14] 李化义，张迎春，李葆华，等. 高精度转动惯量测量仪分析与设计[J]. 计量学报, 2004,25(3): 250-253.

[15] 冯艳秋. 转动惯量测量测试系统设计及精度分析[D]. 长春:长春理工大学,2011:25-39.