同步压缩-交叉小波变换及滚动轴承故障特征增强
2018-06-25李继猛黄梦君江国乾
李继猛, 黄梦君, 谢 平, 江国乾, 陈 萌, 何 群
(燕山大学 电气工程学院 河北省测试计量技术及仪器重点实验室, 河北 秦皇岛 066004)
1 前 言
滚动轴承是机械设备最为关键的部件之一,轴承的缺陷和损伤不仅直接影响机械设备的稳定运行,而且会造成整个设备的损坏。据统计,机械故障的发生很多都是由于滚动轴承的损坏所引起的,所以对轴承的故障诊断有重要的工程意义。但轴承故障特征微弱,由于受到滚动轴承的工作环境和工作机理的影响,一般采集的振动信号通常是非平稳、非线性的,加上背景环境噪声的干扰,故障信号的信噪比低,增加了轴承故障特征的识别难度,使得故障特征难于提取。文献[1]提出小波变换和独立分量分析相结合的方法来诊断滚动轴承的早期故障;文献[2]通过小波变换,将单通道信号分解后重构,成功分离复合故障特征信息;文献[3]提出一种改进多阈值小波包的去噪算法,解决了单一阈值对噪声去除不完全和对一些有用信号无差别去除的问题。然而这些方法大部分是在小波变换的基础上来进行故障诊断的,故而存在小波基函数选择困难和时频分辨率较低的缺点。时频分辨率较低使得信号特征在时频图谱上相对较模糊,对轴承的故障诊断精度产生影响。因此,提高小波变换的时频分辨率是当前亟需解决的关键问题。
同步压缩小波变换(synchrosqueezing wavelet transform,SWT)[4]是一种时频重排的新方法。通过对信号的小波变换系数进行重分配,可以将信号时频谱上的能量聚集到信号的真实瞬时频率附近,达到消除干扰项,提高信号时频分辨率的目的。相较于传统小波变换,SWT具有高的时频分辨率。文献[5]将SWT运用到地震信号分析中,对比一般的小波变换,SWT在地震信号中的更有优势;文献[6]利用SWT方法,对风电功率信号进行了处理,然后采用神经网络的方法进行建模,实现对风电功率的预测;文献[7]将SWT算法引入土木工程领域中,用来识别拉索的瞬时频率。然而这些文献并没有考虑SWT之后的去噪问题使得最后的结果中仍然存在较多的噪声干扰。交叉小波变换(cross wavelet transform, XWT)建立在小波分析理论基础之上,在时频域内分析2个非平稳信号之间的相关性[8],其被广泛应用于气象、医学等多种领域[9~12]。考虑到振动信号中的噪声具有随机性和互不相关性,通过XWT可以实现时频域内噪声消除,从而提高信噪比。
综合上述2种方法的优点,提出基于同步压缩-交叉小波变换(synchrosqueezing-cross wavelet transform, SXWT)的故障特征提取方法,提高故障信号信噪比和时频分辨率,增强故障特征,并将其运用到轴承故障诊断中。仿真与实测信号分析结果表明,该方法可以实现轴承特征频率的提取与增强,有助于滚动轴承故障的精确诊断。
2 同步压缩-交叉小波变换
2.1 同步压缩变换
SWT是以小波变换为基础的一种时频重组分析算法,首先对信号x(t)进行连续小波变换(continuous wavelet transform, CWT):
(1)
式中:a为尺度因子;b为平移因子;t为时间;ψ*(t)为小波基ψ(t)的共轭。

(2)
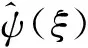
(3)

(4)
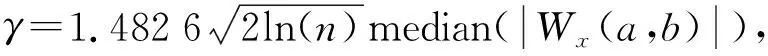
2.2 交叉小波
对于一路能量有限信号x(t),其CWT如式(1)所示,对于两路信号x(t)和y(t),它们之间的XWT定义为
(5)
实际分析中,通常采用交叉小波尺度谱对非平稳信号进行分析,其定义为
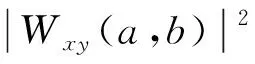
(6)
式中“*”表示取共轭。
XWT可以得到2个信号相关性在时频域中分布状况,其变换系数表示这两个信号在时频域中存在相关性的大小,其值越大说明相关程度越密切。噪声由于具有随机性和互不相关性,在XWT中对信号分析的影响较小。
2.3 同步压缩-交叉小波变换原理
当滚动轴承发生故障时,其损伤部位与其他元件接触时会产生冲击,在轴承连续旋转时将产生周期性冲击。
轴承故障发生的位置不同,产生的冲击信号的周期也不一样。如果能够准确地识别这种冲击周期的大小,就可以实现轴承的故障预警与检测。然而滚动轴承工作时,存在噪声等其它信号的干扰,实现微弱冲击信号的识别存在一定的难度。
因此,结合SWT高分辨率的优势和XWT提高信噪比的优点,提出了SXWT的方法,以实现对滚动轴承的故障诊断。该方法的特征提取步骤如下:
1) 对长度为2n的信号均分长度为n的两段信号,然后再做希尔伯特包络解调处理;
2) 分别对两段信号进行CWT,得到小波系数Wx(a,b),Wy(a,b);然后再按照式(4)分别对两段信号得到的小波系数进行SWT,则得到信号的同步压缩小波变换系数为:Tx(ω,b)、Ty(ω,b);
3) 将求得的同步压缩小波变换系数Tx(ω,b)、Ty(ω,b)输入到XWT里面,按照式(5)、式(6)得到交叉小波尺度谱。应用交叉小波变换后的尺度谱对故障信息识别,进行故障诊断。
3 仿真信号检测分析
为了验证本文所提方法的有效性,建立轴承外圈故障仿真模型如下:
(7)
式中:t1为振荡衰减信号的衰减时间;α=1 000为共振衰减系数;f1=2 000 Hz为共振频率;f2=30 Hz为调制频率;fm=100 Hz为故障频率;采样频率为fs=12 000 Hz;n(t)为高斯白噪声。取信号前6 000个点组成第一路信号,后6 000个点为第二路信号,分别给这两路信号加上信噪比为5的随机噪声。信号未加噪声和加噪声之后的时域波形图如图1所示。显然,从加噪声之后的时域图中无法直接得到有用信息。
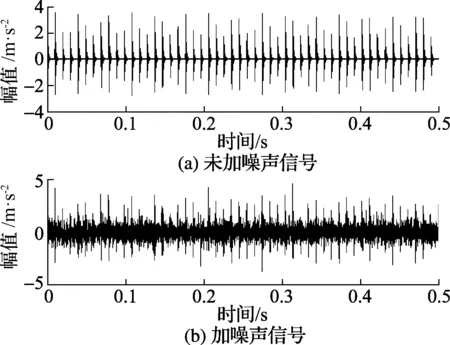
图1 仿真信号时域图
采用Morlet小波对信号进行CWT和XWT。其中CWT图和SWT图都是显示的第一路信号的图谱。
图2(a)为CWT谱,从大量的噪声分布中初步可以发现故障频率(100 Hz)的存在。对比图2(a)和图2(b)所示的XWT谱噪声明显减少,能够区分故障频率及其倍频。充分说明XWT对两个信号的相关性分析具有很强的时频分析功能,但由于CWT方法本身在尺度/频率方向上存在模糊现象,加上低频区噪声过多,对故障频率干扰较大。故XWT同样无法清晰分辨其具体频率。
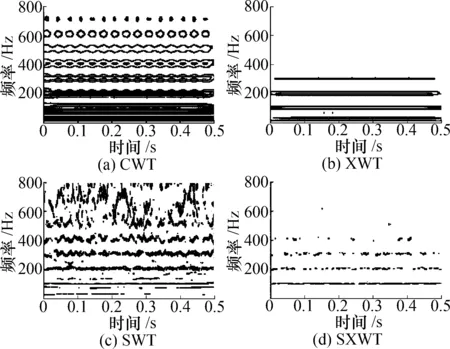
图2 仿真信号时频图
图2(c)是SWT图,对比图2(a)和从图2(c)可以看出SWT低频处噪声得到很好的抑制,且对频率成分进行了压缩,这个步骤消除了CWT的时频模糊现象从而提高了信号的频率分辨率。但和CWT的图谱一样,SWT在高频处噪声依旧很大,对故障频率的提取有很大干扰。图2(d)是本文所用SXWT得到的图谱,相较于图2(b)和图2(c),图2(d)中的随机噪声基本消除,100 Hz的故障频率及其倍频清晰可见。仿真分析结果说明,SXWT充分发挥了XWT与SWT的优点,既消除了噪声干扰,又提高了时频分辨率。
4 轴承故障特征实例
为了对SXWT的有效性进行进一步验证,选取美国凯斯西储大学的滚动轴承数据进行分析。该实验平台的加速度传感器垂直固定在驱动端的轴承座上方。轴承型号为SKF6205,采样频率为12 000 Hz,轴承故障采用电火花加工单点损伤,其中内外圈故障选择的故障直径为0.711 2 mm。正常状态和发生内外圈故障时,都选择的是转速为1 796 r/mim且处于空载状态的数据。其中第一路数据为前4 096个点,第二路数据为后面4 096个点。分别对两路数据做包络解调预处理之后再进行分析。
根据轴承的型号参数,经计算在1 796 r/mim的转速下其特征频率如表1所示。

表1 滚动轴承特征频率 Hz
采用CWT、XWT、SWT和SXWT 4种方法对正常轴承进行对比分析,结果分别如图3所示。由图3可知,从CWT中特征频率(30 Hz)基本上被噪声淹没;XWT相对CWT更加集中,这是由于减少了大部分高频随机噪声的干扰,但较低的时频分辨率使转频成分依旧难于分辨;SWT图谱少数频率成分清新可见,时频分辨率明显提高,然而依旧存在部分高频噪声干扰;而从本文提出的SXWT上可以清晰地看到30 Hz特征频率(转频)成分,符合轴承正常运行状态。
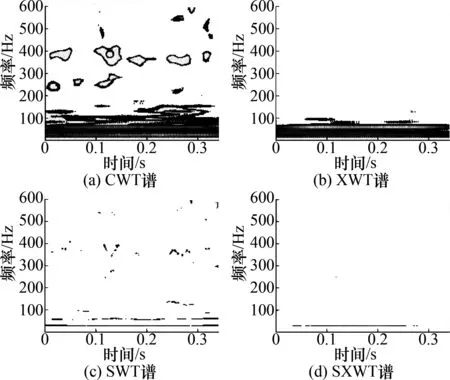
图3 正常轴承信号时频图
同样,采用4种方法对轴承内圈和外圈故障进行诊断分析,结果分别如图4和图5所示。对比发现:由于随机噪声或低时频分辨率影响,CWT无法准确检测到故障特征频率;XWT和SWT检测效果略好,但依然有其他频率成分干扰;而本文所提的SXWT方法能够清晰的检测到外圈故障特征频率107 Hz和内圈故障特征频率162 Hz,表现出最佳的检测性能,这更加说明了SWT的高时频分辨能力和XWT优良的时频去噪能力。
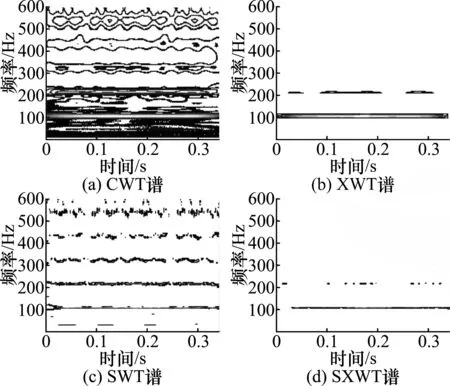
图4 外圈故障信号时频图
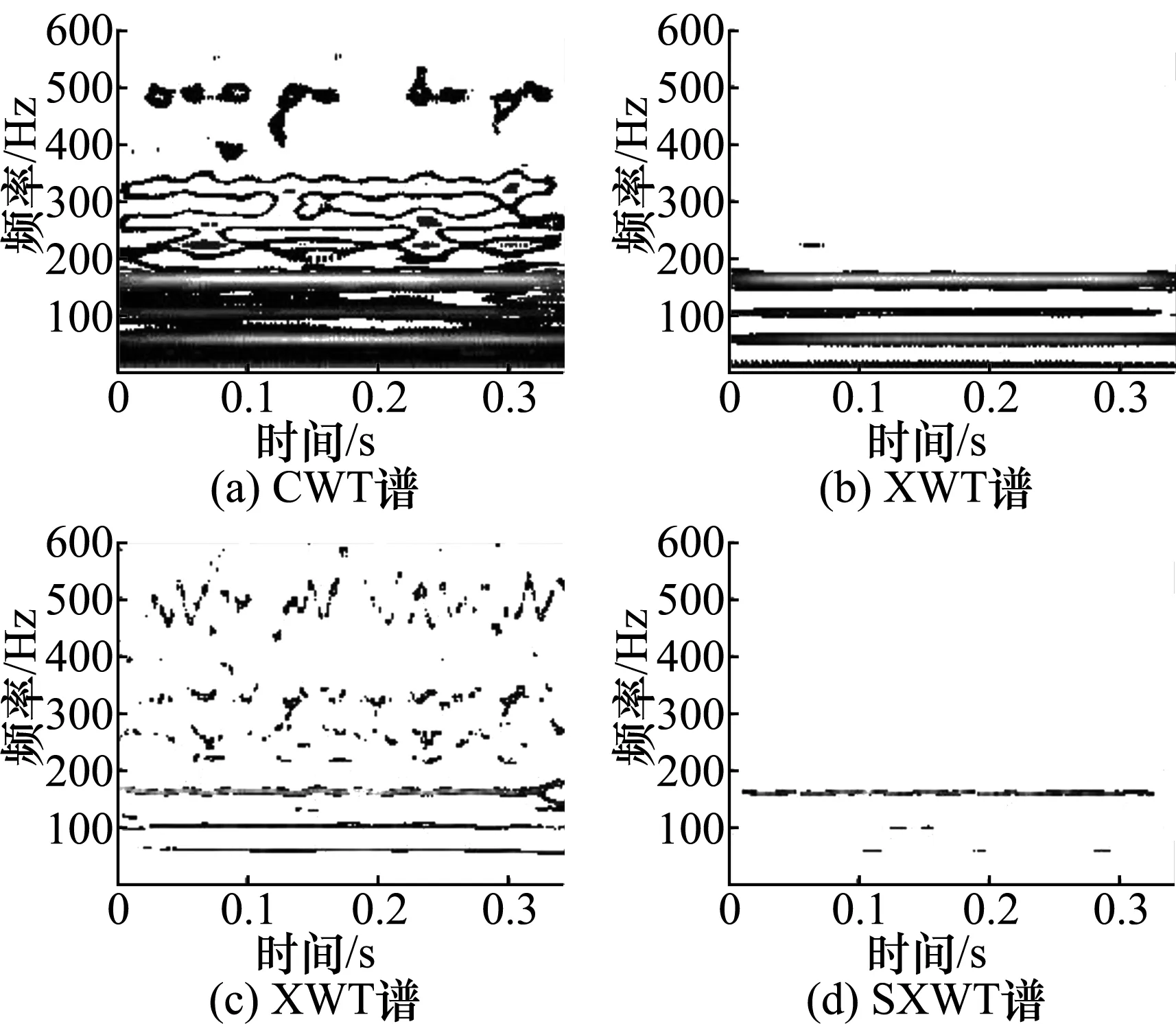
图5 内圈故障信号时频图
对比图3,图4和图5可以看出,轴承振动信号经过CWT后可以大致得出故障频率,但是噪声较多,特征频率容易被噪声掩盖;经过XWT处理后的图谱,明显减少了高频随机噪声的影响,但如图3(b)所示,低频干扰如果过大,特征频率同样容易被淹没;SWT的时频集聚性及对低频噪声的消除效果明显高于CWT和XWT,可高频噪声也相对较多。使用本文提出的SXWT的方法,能有效滤除信号中随机噪声的干扰,增强故障特征频率,从而实现精确可靠的故障诊断。
5 结 论
(1)基于SXWT的轴承特征提取方法通过SWT对信号的频率进行压缩变换,消除小波变换在时频上的频率模糊现象;进一步,利用XWT对信号进行消噪处理,达到突出轴承的特征频率目的。
(2)使用SXWT方法对轴承的正常和内外圈故障进行故障诊断。结果表明,该方法可以很好地消除振动信号中的非周期分量和随机干扰,增强故障特征频率。对比CWT,XWT和SWT,SXWT的特征频率在时频图上聚集性更好,噪声影响更少。
[参考文献]
[1] 吴强, 孔凡让, 何清波. 基于小波变换和ICA的滚动轴承早期故障诊断[J].中国机械工程, 2012, 23(7): 835-840.
[2] HONG H, LIANG M. Separation of fault features from a single-channel mechanical signal mixture using wavelet decomposition[J].MechanicalSystemsandSignalProcessing, 2007, 21(5): 2025-2040.
[3] 王洪斌, 王世豪, 籍冰朔, 等. 基于改进多阈值小波包的去噪算法及应用[J]. 计量学报, 2016, 37(2): 205-208.
[4] Daubechies I, LU J, WU H T. Synchrosqueezed Wavelet Transforms: an Empirical Mode Decomposition-Like Tool[J].AppliedandComputationalHarmonicAnalysis, 2011, 30(2): 243-261.
[5] WANG P, GAO J H, WANG Z G. Time-Frequency Analysis of Seismic Data Using Synchrosqueezing Transform[J].IEEEGeoscienceandRemoteSensingLetters, 2014, 11(12):2042-2044.
[6] 厉祥. 基于SST和神经网络的风电功率预测[D] 武汉: 武汉科技大学硕士论文, 2013.
[7] 刘景良, 任伟新, 王佐才. 基于同步挤压和时间窗的时变结构损伤识别[J]. 振动工程学报, 2014, 27(6):835-841.
[8] 张进, 冯志鹏, 卢文秀, 等. 交叉小波变换在水轮机非平稳信号分析中的应用[J]. 中国电机工程学报, 2010, 30 (23): 84-89.
[9] 孙卫国, 程炳岩.交叉小波变换在区域气候分析中的应用[J]. 应用气象学报, 2008, 19(4):480-487.
[10] 林志一,陈希武,周秀英,等. 采用小波变换的功率测量方法[J]. 计量学报, 2003, 24(1): 52-55.
[11] de Michele G, Sello S, Carboncini M C,etal.Cross-correlation time-frequency analysis for multiple EMG signals in Parkinson’s disease:a wavelet approach[J].MedicalEngineeringandPhysics, 2003, 25(5): 361-369.
[12] Turbelin G, Ngae P, Grignon M. Wavelet cross-correlation analysis of wind speed series generated by ANN based models[J].RenewableEnergy, 2009, 34(4): 1024-1032.
