基于改进差分进化算法的运动想象脑机接口频带选择

胡春海， 李 涛， 刘永红， 齐 凡

(燕山大学 测试计量技术及仪器河北省重点实验室， 河北 秦皇岛 066004)

1 引 言

脑机接口(brain computer interface, BCI)是一种不依赖外围神经和肌肉组织的人机通信系统[1]。脑电信号(electroencephalogram，EEG)反映了大脑功能状态和大脑组织电活动，所以EEG的识别与处理在BCI系统中得到了广泛应用[2,3,15]。肢体运动或运动想象会引发大脑的EEG特定频带能量的降低或升高，这种现象被称为事件相关去同步现象(event-ralated desynchronization, ERD)和事件相关同步现象(event-ralated synchronzation, ERS)，而ERDERS现象主要体现在μ节律频段(8～13 Hz)和β节律频段(13～30 Hz)的波动[4]。脑机接口中根据运动想象信号来判别受试者的运动想象模式，由于个体之间大脑不同，对ERDERS事件的最优响应频带也有所不同，所以通常采用的(8～30 Hz)频带并不是一个高效的特征提取频带。

脑机接口研究的关键在于提取有效特征和提高分类识别率，很多研究者采用各种优化算法对脑机接口进行通道选择和特征向量选择。文献[5]提出一种基于稀疏组lasso的脑机接口通道和特征选择方法，同时对通道和特征进行优化选择。文献[6]提出一种基于改进的遗传算法与RC最大化方法的脑机接口通道选择。文献[7]提出一种基于Relief-SBS的脑机接口通道选择算法，该算法结合了Relief的统计相关性原理和顺序向后算法的迭代思想对EEG通道进行优化选择。文献[8]提出一种基于回溯搜索优化算法的运动想象脑机接口频带选择方法，虽然分类结果优于(8～30 Hz)滤波的方法，但是该算法收敛到最优频带的时间开销太大。

本文将实数编码的差分进化(differential evolution, DE)方法用于EEG处理，并提出多策略变异算子和时变非线性交叉因子的差分进化(multi-strategy mutation operator and time-varying nonlinear crossover factor differential evolution, MSTVNDE)算法，充分利用DE算法良好的全局寻优能力，并解决了DE算法容易陷入局部最优导致无法收敛到全局最优的弊端，实现了个体频带的最优选择。

2 MSTVNDE差分进化算法

标准DE算法[9]包括种群初始化，变异，交叉，选择操作等步骤。DE算法的搜索性能与变异算子和交叉因子的选取密切相关，MSTVNDE算法从变异策略和交叉参数两方面对DE算法进行了改进。首先，用凸二次函数融合了DE/rand/1与DE/best/1两种变异策略，使变异策略能够随着迭代过程而调整;其次，对CR因子取值进行动态调整，以满足不同迭代时期的需求。

当采用DE/rand/1方案时，参与变异的频带是随机产生，并没有利用适应度的信息，全局搜索能力强，但收敛速度慢;当采用DE/best/1方案时，保留了本代最优频带，收敛速度快，但是容易陷入局部最优[10]。本文融合了这两种不同的变异方式，采用一种基于凸二次函数的多策略变异算子(multi-strategy mutation operator, MSMO)：

(1)

m=-[(s/Smax)2-2(s/Smax)+1]

(2)

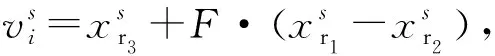
CR因子取值会影响整个搜索过程的收敛速度和最优频带搜索成功率。在进化前期，利用较小的CR因子舍弃较差的个体，保留更多的变异个体;在进化后期，为了避免陷入局部最优，需要利用较大的CR来提高种群的多样性[11]。结合高斯函数，提出一种时变非线性CR因子(time-varying nonlinear crossover factor, TVNCF)取值方法：

(3)

CRmin和CRmax为交叉因子的最小取值和最大取值，通过参数σ对CR的增长曲线进行调节，σ一般取值在[4，6]。在整个迭代过程中，CR因子从CRmin逐渐增加到CRmax。当s=1时，CR因子约为CRmin，父代频带xij对尝试频带uij的贡献多，保证了个体多样性，提高了算法的全局搜索能力;当s=Smax时，CR因子约为CRmax，变异频带vij对uij的贡献多，可以避免陷入局部最优，同时加快了收敛速度。

3 基于MSTVNDE算法的EEG信号

处理

脑机接口信号处理的主要流程有EEG信号预处理、特征提取、特征识别，采用MSTVNDE算法对脑机接口进行频带选择的系统由4个部分组成。首先，采用MSTVNDE算法完成滤波频带选择;其次，使用IIR椭圆带通滤波器对多通道EEG信号进行子带滤波;然后，对滤波后的EEG信号计算共空间模式滤波器参数，并根据该参数进行空间滤波，提取特征向量;最后，将输入测试样本的特征向量输入分类器进行分类识别。分类正确率作为个体的适应度值，经过多次差分进化得到个体最优频带和最大适应度值。

3.1 基于MSTVNDE算法的频带选择

采用MSTVNDE算法对频带进行优化选择，种群中的个体表示为[Pb1，Pb2]。根据ERS/ERD现象把搜索频带限制在(8～30 Hz)，则个体的搜索下限为[8,8]，上限为[30,30]。设置种群大小Np=10，每个频带个体间隔2 Hz，且有2 Hz的频带重叠;个体维数D=2，最大迭代次数N=100;变异因子F=0.5，交叉因子CRmin=0.1和CRmax=0.8，参数σ=5。

3.2 基于CSP的特征提取

采用CSP算法[12]作为特征提取算法，CSP是一种从多通道EEG信号中提取事件相关去同步信号成分的有效方法。设EEG源信号为X，使用该滤波器对EEG数据进行滤波，得到空间滤波后的EEG信号Z。由下式对滤波后的信号计算特征向量：

(4)

使用MSTVNDE算法得到进化频带[Pb1，Pb2]，利用进化频带对EEG信号滤波，用滤波信号计算CSP滤波器的滤波参数W，用频带滤波后的EEG信号输入CSP滤波器，提取2m维特征向量。

3.3 LDA特征识别

LDA算法[13]将高维特征向量投影到最佳分类空间，投影后的特征向量能达到较大的类间离散度和最小的内类离散度，使得特征向量具有最佳可分性。基于MSTVNDE算法的最优频带选择方法中，将LDA的分类正确率作为适应度值，从而引导搜索方向。

4 实验及结果分析

采用BCI competition III-dataset 4a[14]的数据集对本文所提算法进行验证，数据集记录了5个健康受试者(包含aa，al，ay，aw，av)发生ERDERS事件的运动想象EEG信号。截取事件发生后原始EEG信号在3.5 s内的有效数据点进行实验，并选取位于大脑中部区域内的部分导联作为实验导联集合：(1)选取导连CFC5，CFC3，CFC4，CFC6，C5，C3，C1，C2，C4，C6，CCP5，CCP3，CCP4，CCP6的数据作为14导联数据集;(2)在14导联数据集基础上增加11个导联CFC7，CFC1，CFC2，CFC8，T7，Cz，T8，CCP7，CCP1，CCP2，CCP8的数据作为25导联数据集。

本文在Pentium E6500 CPU，2G RAM，WIN7-32bit， Python 3.5系统实验平台下进行了常规(8～30 Hz)频带滤波的特征提取分类实验、基于MSTVNDE算法的频带优化方法实验，并对分类正确率进行了对比。

实验1：对3个不同导联集合的数据集，采用(8～30 Hz)的带宽进行滤波，CSP提取6维特征向量，LDA对特征向量分类识别。进行10次5倍交叉验证，最终结果如表1所示。从表1可以看出，受试者aa、av、aw、ay使用(8～30 Hz)频带滤波后的EEG信号不能提取到有效的特征向量，使得分类正确率都比较低;同时可以看到，导联的减少并没有使分类正确率大幅降低，在少数导联条件下受试者aa、al、av、ay的分类正确率反而升高了，这说明所选导联集合去除了冗余导联，选出了与信号分类更加相关的通道。

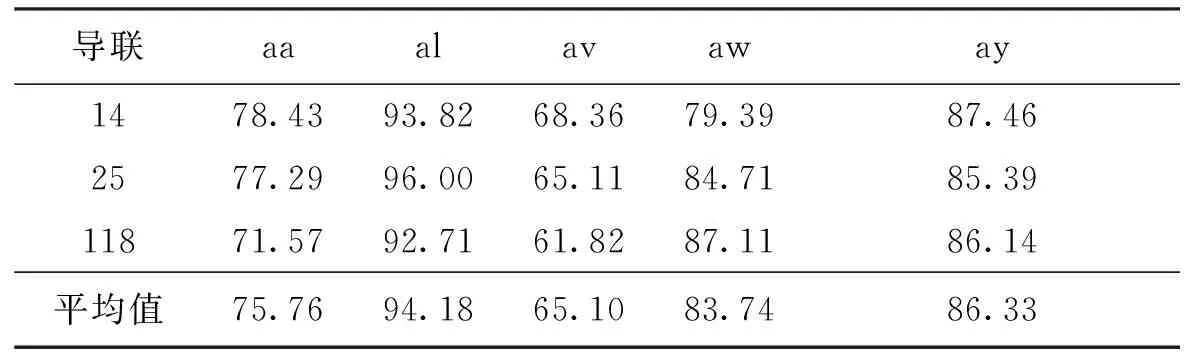
表1 使用(8～30 Hz)频带的分类正确率

实验2：在基于MSTVNDE算法的频带优化方法中，使用IIR椭圆带通滤波器滤波，CSP算法提取信号的1维特征向量，LDA完成特征向量的分类识别。同样进行10次5倍交叉验证，实验结果如表2、表3和图1、图2所示。MSTVNDE算法得到的5个受试者最优频带如表2所示。可以看出不同的受试者最优频带分布不同，这些频带大都集中在(9～15 Hz)。对于同一个受试者，不同的导联集合也会影响最优频带的分布，表明MSTVNDE算法能够根据所用的通道集合自适应地确定个体最佳频带。

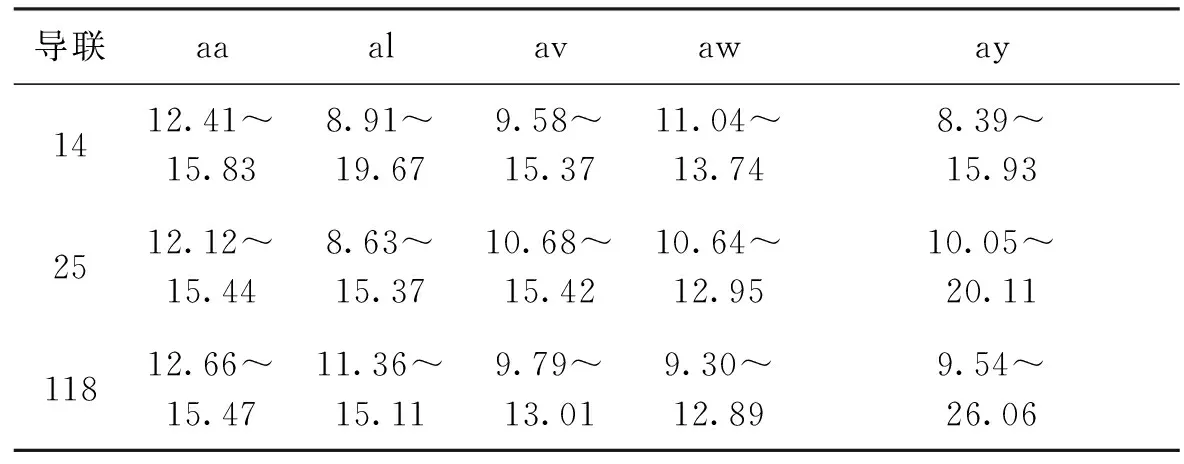
表2 MSTVNDE算法频带寻优结果

表3显示了使用最优频带滤波的分类正确率，对比表1发现，采用MSTVNDE算法，所有受试者的平均分类正确率分别提升了14.27%，4.07%，13.08%，12.04%，6.65 %，其中受试者aa提升最明显。

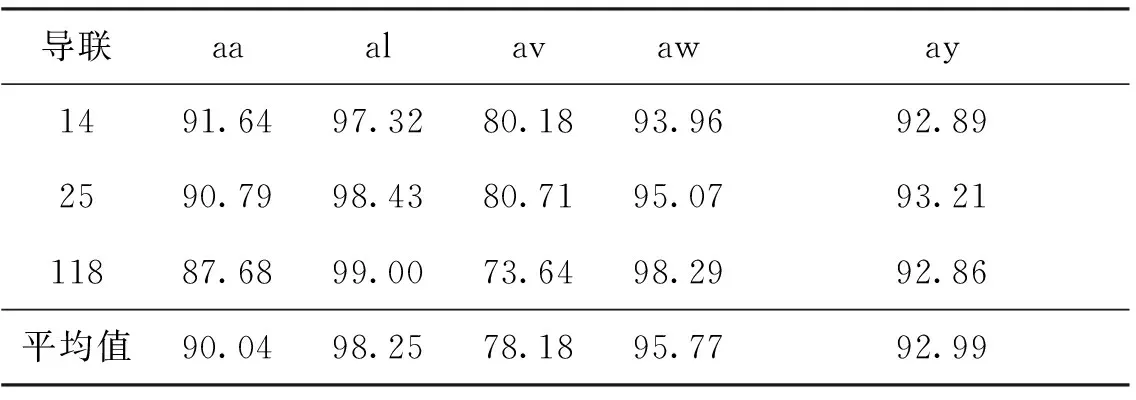
表3 使用个体最优频带的分类正确率

图1为5个受试者的收敛代数箱线图，从左往右依次是每个受试者使用14、25、118导联数据集的结果。图2是5个受试者使用该3个导联数据集在不同迭代次数时消耗的平均时间。从图1可以看出，使用MSTVNDE算法后，5个受试者均在65次迭代内全部收敛。

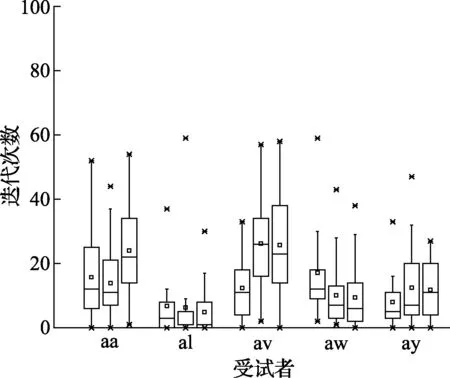
图1 收敛代数

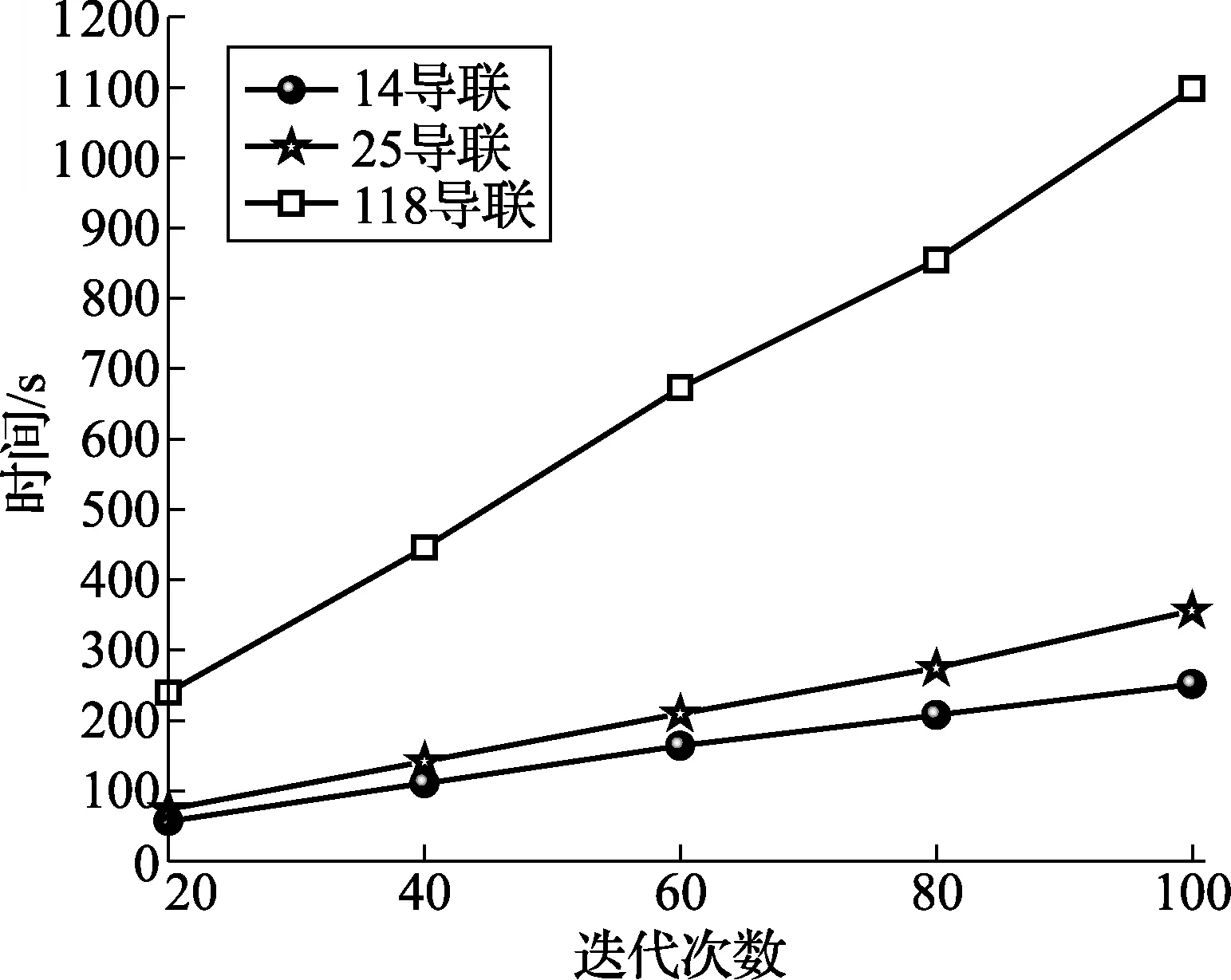
图2 不同导联集合迭代次数和时间的关系

本文使用MSTVNDE算法对5个受试者进行了频带优化实验，采用14导联数据，约180s可以收敛到最佳频带，采用最优响应频带的平均分类正确率比(8～30 Hz)宽带滤波的方法要高10.03%。与同样采用频带选择的方法[8]相比，本文在分类正确率上提高了0.15%和2.06%，且收敛时间大幅减少，说明该算法能够实时有效地选择个体最优频带。

5 结 论

本文提出一种基于MSTVNDE算法的运动想象EEG信号最优频带选择方法。克服了运动想象信号处理过程中不能根据受试者个体差异选择滤波频带，需要人工选择的困难;解决了差分进化算法容易陷入局部最优而无法收敛到全局最优等问题。提出的方法能够快速有效地选择个体最优响应频带，在系统分类正确率和收敛速度方面都有了很大改善，为基于运动想象脑电信号的脑机接口在线应用提供了一种可行方案。

[参考文献]

[1] Wolpaw J R, Birbaumer N, Mcfarland D J,etal. Brain-computer interfaces for communication and control[J].ClinicalNeurophysiology, 2002, 113(6): 767-791.

[2] Hohne J, Holz E, Staigersalzer P,etal. Motor imagery for severely motor-impaired patients: evidence for brain-computer interfacing as superior control solution[J].PlosOne, 2014, 9(8):1-11.

[3] 张立国, 张玉曼, 金梅, 等. 基于盲源分离的P300脑电信号特征提取方法的研究[J]. 计量学报, 2015, 36(6): 634-637.

[4] Park C, Looney D, Rehman N U,etal. Classification of Motor Imagery BCI Using Multivariate Empirical Mode Decomposition[J].IEEETransactionsonNeuralSystemsandRehabilitationEngineering, 2013, 21(1): 10-22.

[5] 王金甲, 薛芳, 李慧. 基于稀疏组lasso的脑机接口通道和特征选择研究[J]. 仪器仪表学报, 2015, 36(8):1831-1837.

[6] He L, Hu Y, Li Y,etal. Channel selection by Rayleigh coefficient maximization based genetic algorithm for classifying single-trial motor imagery EEG[J].Neurocomputing, 2013, 121(18):423-433.

[7] 单海军, 朱善安. 基于Relief-SBS的脑机接口通道选择[J]. 生物医学工程学杂志, 2016,(2):350-356.

[8] 魏中海, 魏庆国.基于回溯搜索优化算法的运动想象脑机接口频带选择[J].科学技术与工程, 2015, 15(14):70-75.

[9] Das S, Mullick S S, Suganthan P N. Recent advances in differential evolution — An updated survey[J].Swarm&EvolutionaryComputation, 2016, 27:1-30.

[10] Epitropakis M G, Tasoulis D K, Pavlidis N G,etal.Enhancing Differential Evolution Utilizing Proximity-Based Mutation Operators[J].IEEETransactionsonEvolutionaryComputation, 2011, 15(15):99-119.

[11] Guo S M, Yang C C.Enhancing Differential Evolution Utilizing Eigenvector-Based Crossover Operator[J].IEEETransactionsonEvolutionaryComputation, 2015, 19(1):31-49.

[12] 李明爱, 刘净瑜, 郝冬梅.基于改进算法的运动想象脑电信号识别方法[J].中国生物医学工程学报, 2009, 28(2):161-165.

[13] Blei D M, Ng A Y, Jordan M I,etal. Latent dirichlet allocation[J].JournalofMachineLearningResearch, 2003，3: 993-1022.

[14] Lu N, Yin T.Motor imagery classification via combinatory decomposition of ERP and ERSP using sparse nonnegative matrix factorization[J].JournalofNeuroscienceMethods, 2015, 249:41-49.

[15] 于向洋， 罗志增. 基于小波系数非线性连续函数衰减的脑电信号去噪[J]. 计量学报, 2017,38(6):754-757.