一种数字阵列雷达小视场快速成像方法

唐 琳，孟宏峰，杨经纬，王文晴

(上海无线电设备研究所，上海 200090)

0 引言

随着高速数据采集、传输和高速数字信号处理技术的发展，数字阵列雷达成为新一代雷达技术的一个重要发展方向[1]。该种雷达融合了数字技术和雷达阵列信号处理技术，实现了数字波束形成对传统模拟波束形成的替代，为雷达软件化和智能化提供了重要的实现途径。与传统雷达相比，数字阵列雷达具有更灵活的系统重构能力、更高效的系统资源利用率，具备实现更多任务、更多功能的适应能力[2]。数字阵列雷达瞬时多波束形成能力强、动态范围大，使其在穿墙、探地、安检等近程成像中得到了广泛应用[3-10]。由于近程成像数字阵列雷达的通道众多，因此在通道长时间幅相稳定性和幅相一致性测量中，如何快速评估系统性能指标成为难题。解决该问题的一种切实可行方法是实时测量成像结果的成像性能，考虑到系统性能评估测试应用中通常采用点目标，视场相对较小，因此，可以采用小视场成像来实现性能指标的快速评估。这也使得小视场快速成像在近程成像数字阵列雷达的系统性能评估测试中具有重要地位。

近程成像数字阵列雷达中包含大量的收发通道。天线的安装误差、通道延时和增益的不一致以及时钟信号的不同步将会导致系统出现多通道幅相误差，而回波散射场的球面特性则会导致系统出现RCM(距离单元徙动)幅相误差，两种误差的耦合出现给近程成像数字阵列雷达快速成像带来极大挑战。文献[11-12]研究了快速时域成像方法，利用子孔径划分来实现快速成像，该方法主要关注大场景下RCM幅相误差的快速校准，可以大幅减少SAR成像的计算量，不过由于缺乏小视场约束，且成像过程未考虑多通道幅相误差，成像效率较低，因此不能应用于小视场快速成像；文献[13]研究了基于感兴趣区域搜寻的波数域快速成像方法，通过小视场约束来提高成像方法的时效性，该方法能有效提高成像效率，但依然未讨论多通道幅相误差的校准问题；文献[14]研究了一种能同时校准近程数字阵列雷达多通道幅相误差和RCM幅相误差的成像方法，通过电磁仿真获得多通道幅相误差的粗估计，利用自聚焦算法获得多通道幅相误差的精估计，同时实现RCM幅相误差的校准，该方法能精确实现近程成像，然而电磁仿真和迭代运算量大，依然不能应用到快速成像中。

本文针对系统性能评估测试应用中难以实现小视场快速成像的问题，提出了一种在小视场条件下快速实现数字阵列雷达近程成像的方法。研究了近程成像数字阵列雷达的小视场快速成像方法，针对数字阵列成像雷达的特点，建立了数字阵列雷达的回波信号模型，研究了DBF(数字波束合成)成像中的幅相误差来源，给出多通道幅相误差和RCM幅相误差的校准公式，给出了数字阵列雷达小视场快速DBF成像的模型，通过实验进行验证。

1 信号模型

数字阵列雷达通常由收发通道阵列组件、数据采集组件和信号处理组件组成。其中，收发通道阵列组件负责信号的发射与接收，数据采集组件负责信号的采集，信号处理组件负责信号的处理。由于收发通道具有互易性，本文只考虑接收通道。图1为数字阵列雷达的组成架构。由图可知：目标反射回波经近场传播后由数字阵列天线接收，经高频接收前端组件和中频处理组件下变频和放大后，由数据采集组件采集变成数字信号，最终由信号处理组件在数字域实现成像处理。接收系统的成像处理不仅包括校正数字阵列天线、高频接收前端组件、中频处理组件带来的多通道幅相误差, 还需要校正近场传播带来的RCM幅相误差。

在数字阵列雷达架构下，近程成像数字阵列雷达的回波信号处理主要包括数字正交解调、脉冲压缩、RCM校正和成像处理等处理过程。通常，可假设发射系统发射的信号波形为

s(t)=cos(2πf0t+θ(t))

(1)

式中：t为时间；θ(t)为调制的窄带波形；f0为载频；s(t)为发射的参考信号，经某个点目标反射后，信号被数字阵列天线接收，其中第n个接收阵元接收到的回波信号为

sn(t)= (1+αn)Acos(2πf0(t-τn)+

θ(t-τn)+φn)

(2)

式中：τn为回波延时；φn为第n个接收通道的相位误差；αn为第n个接收通道的幅度误差；A为回波强度；sn(t)为接收到的回波信号。经数字正交解调后，第n个接收通道的信号为

sn1= (1+αn)Aexp(-j2πf0τn+

jθ(t-τn)+jφn)

(3)

图1 数字阵列雷达组成架构Fig.1 Digital array radar structure

式中：j为虚数单位；sn1(t)为回波数字正交解调后的复数信号。脉冲压缩后，第n个接收通道的信号变为

sn2= (1+αn)Ap(t-τn)

exp(-j2πf0τn+jφn)

(4)

式中：p(t-τn)为脉冲压缩中匹配滤波的结果函数；sn2(t)为脉压后的回波信号。τn可能引起RCM，当RCM不明显，且小于单个距离分辨单元时，τn可忽略；在小视场成像中，即使RCM明显大于单个距离分辨单元，也可简单通过插值实现RCM校正，校正后的信号可等效表示为

sn3= (1+αn)Ap(t-τ0)

exp(-j2πf0τn+jφn)

(5)

近程成像数字阵列雷达信号处理总流程如图2所示。图中：第n个接收通道由AD采样后获得的信号为sn(t)，在信号采集组件中首先进行数字正交解调，解调后的信号为sn1(t)，然后对该复信号进行匹配滤波脉冲压缩，获得幅相校准后的复信号sn2(t)，该复信号经RCM校正后，获得无跨RCM的信号sn3(t)，最后由信号处理组件进行幅度与相位的校正，最终实现DBF成像。

图2 近程成像数字阵列雷达信号处理流程Fig.2 Short-range imaging digital array radar signal processing flow

2 成像模型

近程成像数字阵列雷达成像的本质是多个收发通道的同相叠加，因此其成像过程为幅相补偿和校正的过程。经数字正交解调、脉冲压缩和RCM后，近程成像数字阵列雷达通道间相位差主要由τn和φn决定，通道间幅度差主要受αn影响。正由于τn和φn决定的相位误差耦合在一起，才使传统快速成像方法失效。实际上，多通道幅相误差主要由系统本身决定，不随目标位置的变化而变化。RCM误差主要由天线和目标相对位置决定，其值为空变。在系统性能评估测试应用中，目标场景通常很小，在这样的小视场下，通常可认为RCM幅相误差同样不随目标位置的变化而变化。

因此，在小视场条件约束下，近程成像数字阵列雷达多通道幅相误差、RCM幅相误差在场景内都不随目标位置的变化而变化，任意位置的多通道幅相误差和RCM幅相误差都可以通过同一场景内其它位置测得的幅相误差数据补偿。基于该机理，本文给出一种小视场下快速实现数字阵列雷达近程成像的方法，通过采集近程成像数字阵列雷达场景中心目标的数据，实现场景内多通道幅相误差和RCM幅相误差的同时校准和补偿，通过单次FFT (快速傅里叶变换)实现小视场的快速成像。

图3为数字阵列近程成像雷达的成像几何模型，以分析成像系统的幅相误差来源。图中：用于近程成像的均匀稀疏数字阵列天线位于xoy平面；坐标原点o位于阵列中心；r0为目标到阵列中心的距离；θ0为目标方位角；φ0为目标俯仰角。

图3 成像几何模型Fig.3 Geometry model for imaging

在直角坐标系中，目标位置为(r0cosφ0sinθ0,r0cosφ0cosθ0,r0sinφ0)。

对于位于(x,y,0)位置的第n个数字阵列天线阵元，其信号延时为

(6)

式中：c为光速。在原点附近，对延时进行二阶泰勒展开，得

(7)

RCM校正后，信号可等效表示为

sn,ref=(1+αn)exp(jφn)·A0p(t-τ0)

(8)

式中：(1+αn)表示幅度不一致性；τ0为RCM校正后一致的距离延时；第1个指数项为多通道相位误差，对于特定的数字阵列雷达，在特定时间内其保持稳定；第2个指数项为成像所需的相位项，由目标所在位置决定；第3个指数项为近场误差，由目标位置决定；对于场景中心位于(r0,θ0,φ0)的小成像视场，当视场足够小时，视场内的任意点目标为(r,θ,φ)，第3个指数项可认为是固定的。此时，可对场景中心采集到的信号sn,ref进行校正，表达式为

sn,cor=sn3/sn,ref

(9)

校正后的结果为

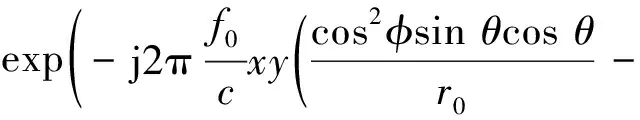
(10)

式中：第1，2个指数项为成像所需的相位项，由目标所在位置决定；第3～5个指数项为校正后的残差，该残差对小视场近程成像效果的影响可忽略不计，其表达式为

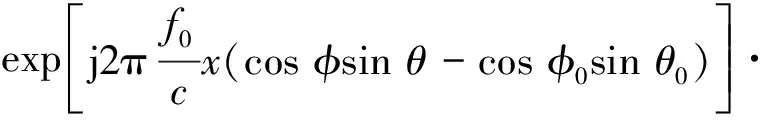
(11)

此时可通过IFFT(快速逆傅里叶变换)来实现目标的成像，即

I=IFFT(sn,cor)=

PSFy((cosφcosθ-cosφ0cosθ0))

(12)

式中：I为DBF成像获得的成像结果；PSFx，PSFy为成像结果的点扩展函数。

3 试验结果

使用IFFT进行快速DBF成像的相位残差通常由目标和数字阵列阵元位置决定，具体包括3项相位残差：第1项残差与方位向阵元位置x2有关，第2项残差与俯仰向阵元位置y2有关，第3项残差与方位与俯仰位置的交叉项xy有关。为评估相位残差对成像结果的影响，进行了如下仿真试验：根据一般的场景设置，视场中心(r0,θ0,φ0)位于(5 m,0 m,0 m)处，视场范围为方位角|θ|≤10°、俯仰角|φ|≤10°，阵列尺寸范围|x|≤1 m，|y|≤1 m，考虑到各项的绝对残差与孔径大小成正比，选取阵元位于x=1 m和y=1 m的位置进行残差仿真结果如图4所示。由图可见：3项残差中最大为0.02λ，对应的相位小于π/25，显然远不能满足成像中相位误差的要求。

为验证数字阵列雷达快速DBF成像方法的有效性，使用了1台Ka波段的数字阵列雷达试验样机进行验证。该样机包含384个接收通道，采用24×16的均匀稀疏阵列天线，天线阵元水平间距为2.620 4λ，垂直间距为1.461 9λ，阵面尺寸约为315 mm×269 mm，采用单音频信号进行了2组成像试验。

第1组试验为点目标成像试验，成像距离为2.5 m，在场景中心位置放置了喇叭天线，采集到相应的校准数据，在视场内移动喇叭天线，采集到成像数据，使用上述方法实现单点目标成像，成像中采用了契比雪夫窗来实现旁瓣抑制。点目标成像结果如图5所示。由图可见，单点目标聚焦效果良好，旁瓣也得到了很好控制，基本在-30 dB以下。

图4 相位残差Fig.4 Phase residual error

图5 点目标成像结果Fig.5 Point target imaging results

第2组试验为陶瓷刀成像试验，成像距离为2.8 m，在场景中心位置放置喇叭天线，采集到相应的校准数据，同时使用喇叭天线照射目标场景，采集到陶瓷刀回波，使用快速DBF成像方法实现成像。图6为陶瓷刀快速DBF成像的结果。由图6可见，本文提出的快速DBF成像方法，对复杂目标依然有效。

图6 陶瓷刀成像结果Fig.6 Ceramic knife imaging results

为进一步评估成像效率，对本文成像方法的运算量进行了评估，运算量主要来源于两部分：一是用于多通道幅相误差和RCM的幅相误差校准和补偿的校准操作；二是DBF成像的IFFT操作。对于Nr×Na的目标场景，校准操作需要6NrNa次浮点运算，DBF成像需要5NrNalog2(NrNa)次浮点运算。对于Nr=1 024，Na=512的场景，成像总共需要50.5 M次浮点运算，优于现有快速成像方法，能很好实现实时成像。

4 结束语

近程成像数字阵列雷达中，多通道幅相误差与近场幅相误差的同时出现会影响雷达成像效率。本文通过研究数字阵列雷达的回波信号模型，建立了近程成像数字阵列雷达的快速DBF成像模型，通过研究DBF成像中幅相误差的来源，提出了一种适用于近程成像数字阵列雷达的小视场成像方法，只需单次FFT即可实现数字阵列雷达的小视场成像。理论分析和试验验证表明：该方法能满足数字阵列雷达小视场的快速成像要求，在系统性能评估测试应用中具有较好的应用前景。值得注意的是，该方法以小视场为前提，未考虑目标空变对RCM幅相误差的影响，同时对相位二阶泰勒展开，因此在相对大视场的应用中成像质量将有所下降，为进一步扩展该方法应用范围，可将本文方法获得数据代替电磁仿真数据进行幅相误差的粗校准，然后使用自校准算法进一步提高成像分辨率或扩大成像视场。

[1] CANTRELL B， GRAAF J D． Development of a Digital Array Radar(DAR) [J]． IEEE Aerospace and Electronic Systems Magazine， 2002， 17(3): 22-27．

[2] 吴曼青．数字阵列雷达及其进展[J]．中国电子科学研究院学报， 2006， 1(1): 11-16．

[3] AHMED S，SCHIESSL S, GUMBMANN A, et al. Advanced microwave imaging[J]．IEEE Microwave Magazine, 2012， 13(6): 1527-3342.

[4] SATO M. Array GPR “Yakumo” and its application to archaeological survey and environmental studies[C]// General assembly and scientific symposium (URSI GASS), Beijing: IEEE, 2014: 1-2.

[5] ZHANG W, HOORFAR A.Three-dimensional synthetic aperture radar imaging through multilayered walls [J]. IEEE Trans. Antennas Propag, 2014, 62(1): 459-462.

[6] LEONARDO C, ALEXANDER G. Concealed weapon detection using UWB 3-D radar imaging and automatic target recognition [C]// Antennas and Propagation (EuCAP), Hague: IEEE, 2014: 2786-2790.

[7] FEDERICO G R, LUISM, JESS G. Real-Time GPU-Based image processing for a 3-D THz radar [J]．IEEE Transactions on Parallel and Distributed Systems, 2017, 28(10): 2953-2964.

[8] MOHAMMAD T G, MATTHEW J. H, M R. D, et al. Wideband Microwave Camera for Real-Time 3-D Imaging [J]．IEEE Transactions on Antennas and Propagation, 2017, 65 (1): 258-268.

[9] FRANK G, ANDREAS S.Short-Range imaging system with a nonuniform SFCW approach [J], IEEE Transactions on Microwave Theory and Techniques, 2017,65(4): 1345-1354.

[10] DAVID M S, DOUGLAS L,et al. Hall three-dimensional millimeter-wave imaging for concealed weapon detection [J]．IEEE Transactions on Microwave Theory and Techniques, 2001, 49(9): 1581-1592.

[11] YANG Z M, SUN G C, XING M D. A new fast back-projection algorithm using polar format algorithm[C]// Asia-Pacific Conference on Synthetic Aperture Radar, Tsukuba: IEEE, 2013: 373-376.

[12] YANG Z M, DONG Q, SUN G C, et al. A fast implementation method for the FFBP algorithm [C]// International Radar Conference, Arlington: IEEE, 2015: 411-414.

[13] 彭学明,王彦平,谭维贤,等.基于感兴趣区域搜寻的机载下视阵列3D SAR波数域快速成像方法[J].电子与信息学报, 2013, 35(7): 1525-1531.

[14] AHMED S S. Electronic microwave imaging with planar multistatic arrays [D]. Erlangen：Friedrich alexander university, 2013.