基于驱动机构作动的太阳翼振动控制原理与实验研究
2018-06-25朱春艳陈必发张美艳唐国安
李 涛,朱春艳,陈必发,张美艳,唐国安
(1. 复旦大学 航空航天系,上海 200433; 2. 上海宇航系统工程研究所,上海 201108)
0 引言
航天器入轨后,太阳翼在驱动机构的作用下转动,实现对日定向,吸收太阳辐射能并转化为电能,为航天器工作提供能量[1]。航天器大型化、轻质化及低刚度的发展趋势对其结构设计及安全运行提出了更高要求[2]。与航天器本体相比,太阳翼具有跨度大、刚度低的特点。由于太阳翼低阶频率ωn很小,衰减项e-ωnζt随时间变化慢,使调姿、定向及变轨中形成的低频振动很难自行衰减。这些振动不仅影响航天器的姿态稳定、定位精度及机载设备的正常工作,严重时还会降低航天器使用寿命甚至导致结构破坏,威胁航天器结构的安全[3]。因此对太阳翼振动抑制开展研究尤为必要。
输入整形技术是一种前馈控制方法,将原始输入信号与依据系统动力学特性设计的特定脉冲整形序列卷积生成新的输入信号,以减小结构在特定频率的振动[4-7]。文献[8]提出了一种在太阳翼根部和表面加装阻尼元件和弹性元件的被动控制方法,具有结构简单、易操作、成本低等优点,是较为成熟的振动抑制方法。文献[9]采用开关式喷射发动机、运用不同的开关策略实现振动抑制,但作动需要消耗工质,不宜频繁采用。近年来,以压电材料为作动器的主动控制方法发展迅速,在航天器柔性结构的振动抑制中得到广泛应用,控制效果显著[10-15]。文献[16]利用反作用飞轮抑制太阳翼振动,取得了不错效果。文献[17]提出了以太阳翼自身配备的驱动机构为作动器的振动控制方法,但仿真模型基于带配重的钢尺,与实际太阳翼结构相差较大,不能很好体现太阳翼动力学特性,且由于采用了较简单的以驱动机构转速为输出量的控制策略,控制结束后驱动机构会发生角度偏移,使太阳翼无法复位且只开展了仿真分析,缺乏实验支撑,振动抑制效果的验证还显不足。
在此基础上,建立了太阳翼真实比例的有限元模型,提高仿真的真实性,并提出通过添加驱动机构角度反馈的转速项来解决驱动机构角度的复位问题,开展了太阳翼缩比模型实验,在控制算法中引入积分环节,实现驱动机构角度反馈转速的等效作用,验证了基于驱动机构作动的振动控制方法的有效性。
1 太阳翼控制方程及振动控制原理
哈勃望远镜由望远镜本体及展开的太阳翼组成,如图1所示。实际中,航天器本体质量远大于太阳翼质量,为简化考虑,在分析太阳翼振动时,将航天器本体视为静止体。展开后太阳翼的简化模型如图2所示,建立随驱动机构运动的非惯性坐标系O-XYZ。

图1 哈勃望远镜Fig.1 Hubble space telescope
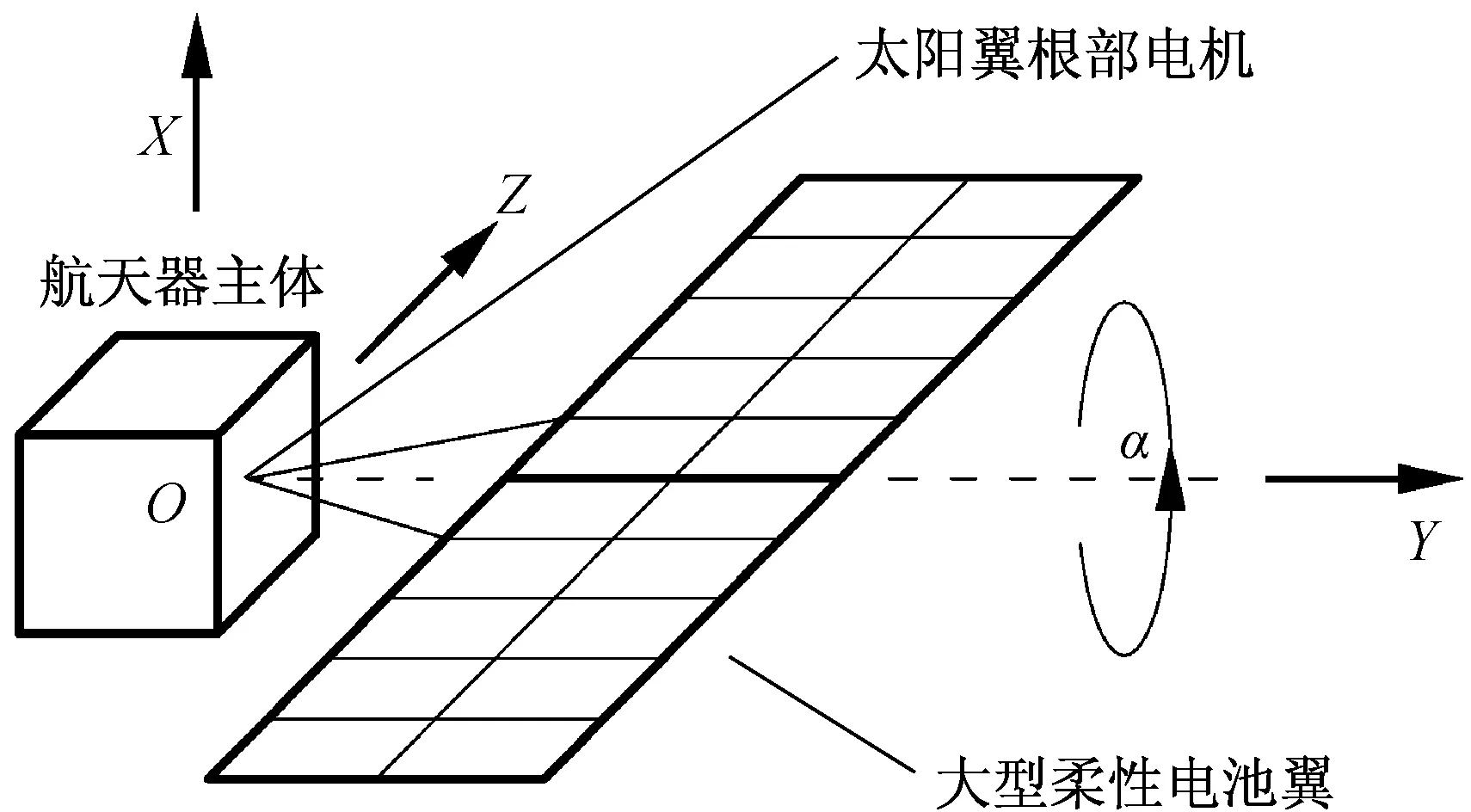
图2 太阳翼简化模型Fig.2 Simplified model of solar array
太阳翼在YOZ平面内横向弯曲振动主坐标下的运动方程[17]为

(1)

(2)
其中,Φ为根部固支的固定界面主模态;M为太阳翼有限元模型的质量矩阵;Ψ为绕Y轴转动的刚体约束模态。
对于线性结构,太阳翼根部弯矩正比于相对位移,可表示为
Mb=κTΦξ
(3)
太阳翼振动主要由一阶横向弯曲振动构成,式(1)可简化为
(4)
式(4)右端为驱动机构提供的输入扭矩,控制律为
(5)
式中:ζa为通过反馈控制力矩添加的人工阻尼系数,ζa>0。将式(5)代入式(4),进一步可得
(6)
式中:ζa起到了加快振动衰减的作用,对小阻尼情况,ζa越大,太阳翼振动衰减速度越快。

(7)
式(7)为驱动机构转速与模态坐标之间的关系,但在实际情况中,ξ1无法测得。根据式(3),在仅考虑一阶模态的情况下,太阳翼根部的弯矩表示为
Mb=κTΦ1ξ1
(8)
根据式(7)和(8),驱动机构转速与太阳翼根部弯矩之间的反馈关系为
Ω=βMb
(9)

2 仿真算例验证
采用太阳翼有限元模型仿真验证振动控制方法有效性,仿真模型如图3所示。太阳翼长度为12 m,宽度为2.8 m,等效均质板的厚度为3.5 mm,总质量为317.5 kg,弹性模量E=7×1010Pa,泊松比ν=0.3。建立空间坐标系O-XYZ,太阳翼在驱动机构的作用下绕Y轴转动。
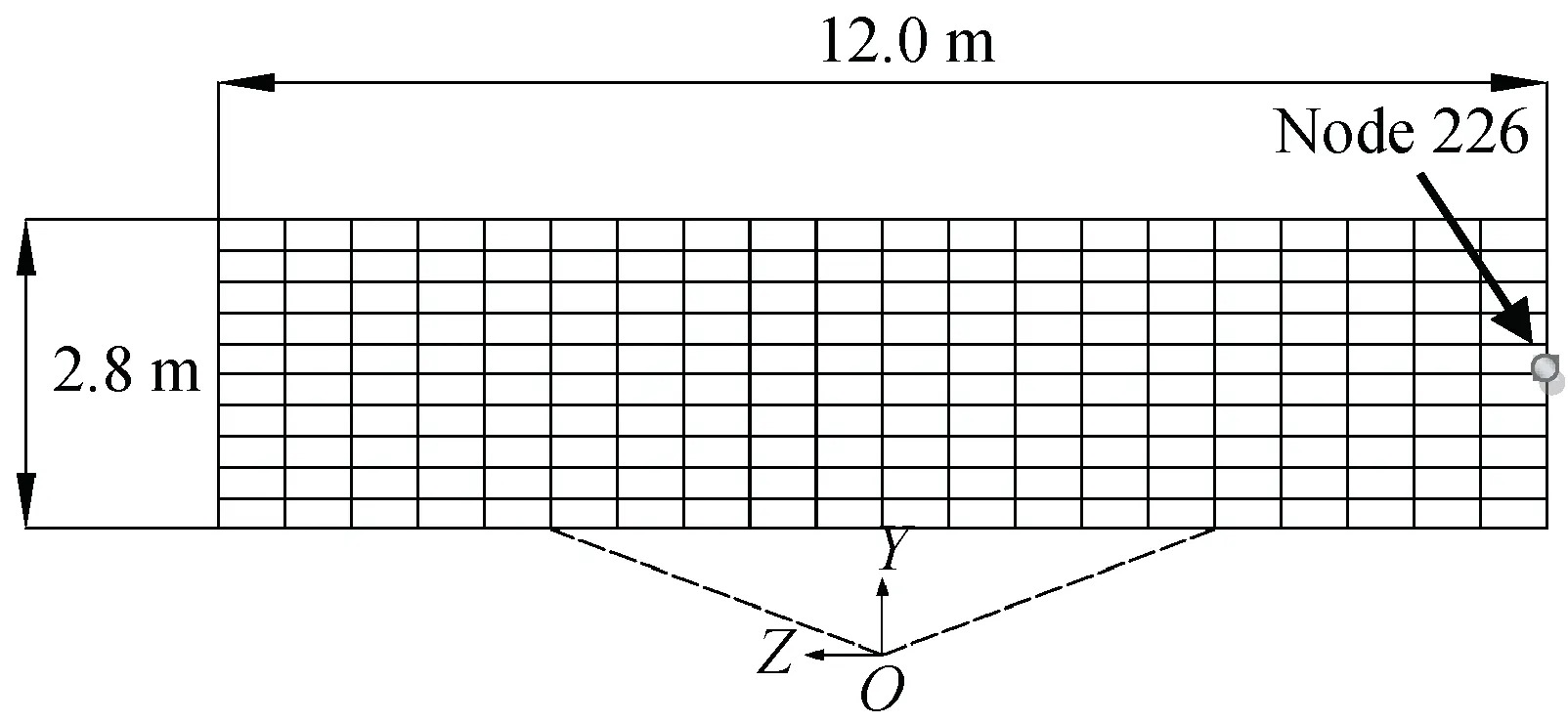
图3 太阳翼有限元模型Fig.3 Finite element model of solar array
太阳翼根部与航天器驱动机构之间的连接简化为1个扭簧,刚度ks=50 kN·m/rad。在进行控制过程仿真时,可利用其计算太阳翼根部的弯矩
Mb=ks(θ1-θ0)
(10)
式中:θ0,θ1分别为驱动机构和太阳翼根部的转角。
太阳翼有限元模型采用Rayleigh比例阻尼,即
C=c1K+c2M
(11)
式中:c1=4.5×10-3;c2=2.7×10-3。太阳翼一、二阶阻尼比为0.005。
仿真过程分为激振阶段和抑振阶段。在激振阶段,模拟太阳翼调姿过程的驱动机构转动,采用梯形信号输入,经过匀加速、匀速、匀减速阶段后停止。由于驱动机构的转速与太阳翼根部弯矩成正比,为保护驱动电机,抑振阶段设定在激振阶段结束后、太阳翼根部弯矩接近于0时开始启动。为此,在激振阶段仿真时,有限元模型的节点位移和速度响应计算结果被导出,作为振动抑制阶段仿真的初始条件。
施加控制时驱动机构的转速为
(12)
式(12)可视为2个节点转角之间的约束关系,用Nastran软件仿真时可利用传递函数输入功能来实现,其标准形式为
(B0+B1p+B2p2)ud+
(13)
对式(12)进行Laplace变换,并按式(13)的形式整理得
(1+η·s+0·s2)L(θ0)+
(-1+0·s+0·s2)L(θ1)=0
(14)
式中:η为控制的增益,η=(βks)-1。
在用Nastran软件进行振动控制仿真时,式(14)可用TF卡的形式表示,并添加到有限元模型[18]。但仿真结果表明,控制过程中驱动机构会发生角度偏移,第226号节点位移如图4所示。

图4 不添加反馈转速第226号节点位移Fig.4 Displacement of node 226 without feedback rotational speed
为使驱动机构正确复位,对式(12)修正,整理得
(15)
式中:-λθ0为由驱动机构转动角度θ0反馈的转速,当θ0没有复位时,提供反向转速使其复位。式(15)也可用TF卡的形式添加至有限元模型,整理得
(λη+η·s+0·s2)L(θ0)+
(-1+0·s+0·s2)L(θ1)=0
(16)
结果表明:当λ=0.1时,既能保证驱动机构控制前后位置一致,又不影响控制效果。添加反馈转速第226号节点位移如图5所示。
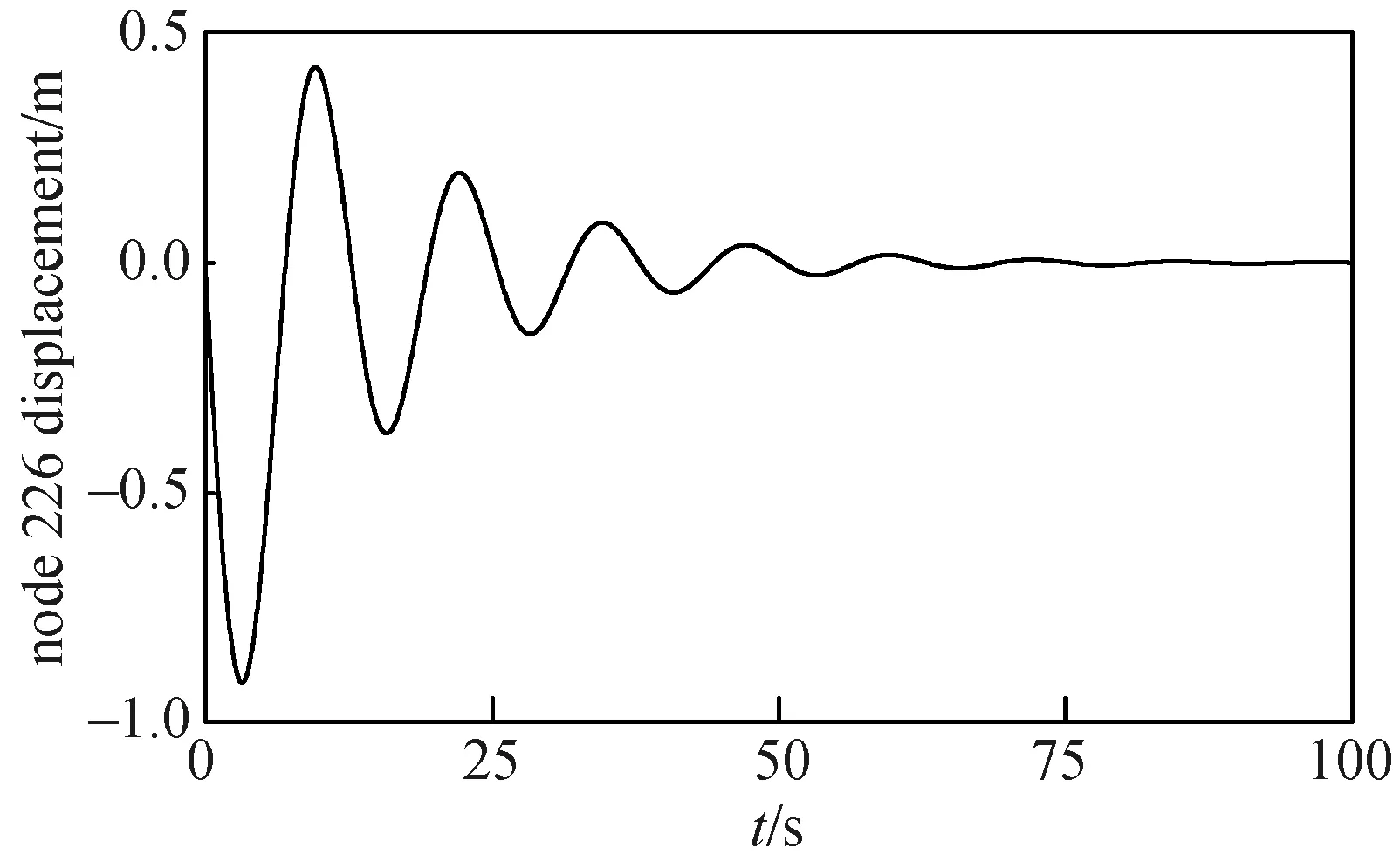
图5 添加反馈转速第226号节点位移Fig.5 Displacement of node 226 with feedback rotational speed
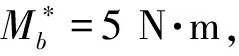
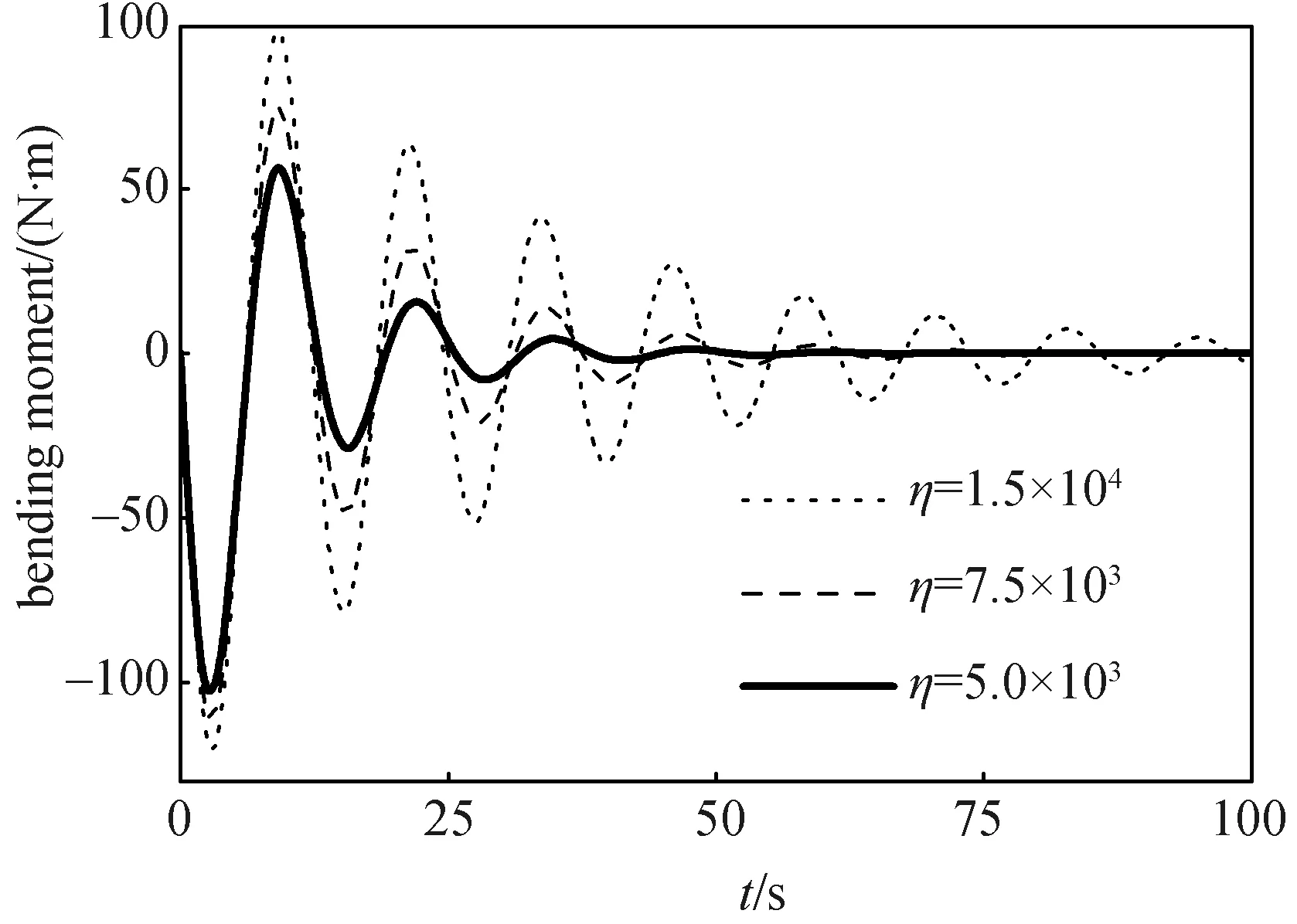
图6 不同增益下太阳翼根部弯矩衰减曲线Fig.6 Attenuation curve of bending moment at the root of solar array with different gains
3 缩比模型实验验证
以太阳翼缩比模型来验证驱动机构抑制振动方法的有效性。太阳翼缩比模型如图7所示。由图可见:太阳翼缩比模型由弹簧钢片制成,中心用夹具夹持,模拟太阳翼调姿转轴,底座通过螺钉与由步进电机驱动的小转台连接,提供驱动力矩;太阳翼侧向放置,弯曲振动与重力方向垂直;装配4个配重,用于调节实验模型的固有频率。经实验测量,太阳翼模型一阶固有频率为0.86 Hz。太阳翼缩比模型的参数见表1。

图7 太阳翼缩比模型Fig.7 Scaled model of solar array

类型参数弹簧钢片长度、高度、厚度/mm×mm×mm750×150×0.3内测配重块质量m1/g220外侧配重块质量m2/g122内测配重块至根部距离l1/mm137.5外测配重块至根部距离l2/mm362.5
缩比模型实验过程如图8所示。由图可知:应变片将测得的根部应变电压输入控制模块,由设计的控制律进行计算,输出相应的驱动电压,以驱动步进电机及转台,向太阳翼提供控制力矩,进行振动控制。实验中,应变片贴在缩比模型根部,其电阻值R=350 Ω,采用全桥电路连接,桥路输入电压为5 V,应变放大仪增益为1 000,滤波模式为低通3 Hz。在线性变形范围内,太阳翼根部弯矩Mb正比于应变放大仪测得的应变电压Uε,根部弯矩根据力及力臂参数计算,可标定应变电压至根部弯矩的转换系数为

图8 缩比模型实验流程图Fig.8 Flow diagram of scaled model
(17)
实验测得kV-M约为0.04 N·m/V。
根据式(9)和(17),转台转速与应变电压之间的关系为
Ω=βkV-MUε
(18)
实验中转台由步进电机驱动。转台转速与电机转速的关系为
Ω=2πN/(60×i)
(19)
式中:N为步进电机转速,r/min;i为电机至转台的减速比,i=180。
实验利用步进电机细分驱动器,放大来自Arduino UNO单片机的脉冲信号,实现对步进电机的精确平稳控制。脉冲信号的频率正比于驱动电压,设定0~5 V的驱动电压,电机便可以在0~285 r/min的转速范围内转动。电机的方向由映射至UNO单片机上数字信号的高低电平控制。驱动电压Udri与电机转速之间的关系为线性的,其表达式为
Ω=2π×285/(60×180)×(Vdri/5)
(20)
结合式(18)和(20),可得电机驱动电压与应变电压的关系为
Udri=γUε
(21)
式中:增益为
γ=5×60×180/(2π×285)×βkV-M
(22)
根据理论分析可知,增益γ越大,振动抑制效果越好。增益的选取也应考虑电机实际的转速能力。当太阳翼根部弯矩Mb最大时,转台转速达到最大值,即应变电压最大时,驱动电压达最大值。经计算,增益最大值γmax=1.3。
应变电压采集过程中存在噪声等干扰信号,因此需对输入信号进行滤波处理。选用巴特沃兹(Butterworth)带通滤波器,该滤波器低通为0.75 Hz,高通为1.5 Hz。为了保护电机驱动器,需要对输出的驱动电压进行饱和限制。完整的控制算法如图9所示。与仿真一样,在实验中,驱动机构存在角度偏移。为解决该问题,在控制算法中增加了积分环节。由经验可得,当积分增益为-0.5时,转台位置在施加控制前后能保持一致,且不影响振动控制的效果。采用固定时间步长的算法,时间步长Δt=0.01 s。实验激振采用梯形信号输入,在1.14 s激振阶段内转台转速Ω变化情况如图10所示。

为验证控制增益对振动抑制效果的影响,选取3组不同的增益(γ=0.3,0.7,1.3)进行振动控制,实验结果如图12所示。
4 结束语
针对航天器太阳翼在调姿或变轨后低频振动衰减速度缓慢的问题,本文以太阳翼自身驱动机构为作动器,产生正比于系统主振动速度的反馈控制力矩,加快振动衰减速度。该方法无需增加额外机构,具有较强的可操作性。在有限元仿真时,通过添加驱动机构角度反馈的转速,并在实验控制算法中引入积分环节,解决了控制结束后驱动机构发生角度偏移的问题。结果表明:基于驱动机构作动的太阳翼振动控制方法能明显减振;对于小阻尼情况,等效的人工阻尼系数越大,振动衰减的速率越快。本文方法能在保证太阳翼不偏离目标位置的同时,有效抑制太阳翼的低频振动。

图9 控制程序框图Fig.9 Block diagram of control program

图10 转台转速曲线Fig.10 Curve of rotational speed of spinning platform
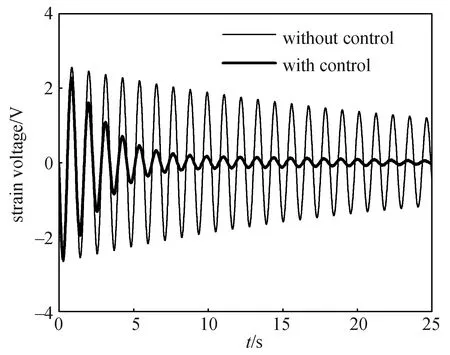
图11 太阳翼根部应变电压衰减曲线Fig.11 Attenuation curve of strain voltage at the root of solar array

图12 不同增益下太阳翼根部应变电压衰减曲线Fig.12 Attenuation curve of strain voltage at the root of solar array with different gains
[1] 袁家军. 卫星结构设计与分析[M]. 北京:中国宇航出版社, 2004.
[2] 黄文虎, 王心清, 张景绘, 等. 航天柔性结构振动控制的若干新进展[J]. 力学进展, 1997, 27(1): 6-19.
[3] 李东旭. 挠性航天器结构动力学[M]. 北京:科学出版社, 2010.
[4] 刘玮, 郭其威, 朱春艳, 等. 柔性航天器舱体搬运时输入整形振动抑制方法和原理试验[J]. 上海航天, 2015, 32(5): 31-34.
[5] 那帅, 朱春艳, 彭福军, 等. 基于输入整形技术的太阳翼调姿残余振动抑制实验研究[J]. 振动与冲击, 2013, 32(7): 107-112.
[6] 朱春艳, 邵济明, 那帅, 等. 太阳电池翼调姿后残余振动抑制的整形器设计[J]. 振动与冲击, 2012, 31(8): 176-180.
[7] 朱春艳, 绍济明, 唐国安. 双输入整形器抑制两轴转动太阳翼调姿后的残余振动[J]. 噪声与振动控制, 2011, 31(6): 1-4.
[8] 许雲淞. 挠性卫星姿态机动及太阳帆板振动抑制研究[D]. 哈尔滨:哈尔滨工业大学, 2014.
[9] 任萱. 人造地球卫星轨道力学[M]. 长沙: 国防科技大学出版社, 1988.
[10] MEYER J L, HARRINGTON W B, AGRAWAL B N, et al. Vibration suppression of a spacecraft flexible appendage using smart material [J]. Smart Materials and Structures, 1998, 7(1): 95-104.
[11] SONG G, AGRAWAL B N. Vibration suppression of flexible spacecraft during attitude control [J]. Acta Astronautica, 2001, 49(2): 73-83.
[12] HU Q L, MA G F. Spacecraft vibration suppression using variable structure output feedback control and smart materials [J]. Journal of Vibration and Acoustics, 2006,(2): 221.
[13] SALES T P, RADE D A, DE SOUZA L C G. Passive vibration control of flexible spacecraft using shunted piezoelectric transducers [J]. Aerospace Science and Technology, 2013, 29(1): 403-412.
[14] WU D, HUANG L, PAN B, et al. Experimental study and numerical simulation of active vibration control of a highly flexible beam using piezoelectric intelligent material [J]. Aerospace Science and Technology, 2014, 37: 10-19.
[15] HALIM D, LUO X, TRIVAILO P M. Decentralized vibration control of a multi-link flexible robotic manipulator using smart piezoelectric transducers[J]. Acta Astronautica, 2014, 104(1): 186-196.
[16] 陈必发,吕亮亮,彭福军,等.利用反作用飞轮抑制太阳电池阵振动的原理和方法研究[J].上海航天,2018,34(1):104-109.
[17] 李涛, 陈必发, 吕亮亮,等. 基于驱动机构作动的柔性附件振动控制原理与算法[J]. 载人航天, 2017, 23(4):482-486.
