考虑小波数相关性的SAR图像去斑算法
2018-06-25陈国忠王廿菊陈重华朱少杰
陈国忠,王廿菊,崔 雷,陈重华,孙 杰,朱少杰
(1. 上海卫星工程研究所,上海 201109; 2. 上海航天技术研究院,上海 201109)
0 引言
SAR(合成孔径雷达)发射的相干信号之间会使图像产生相干斑点噪声(speckle noise),严重影响SAR图像的判读效果,甚至可能导致地物特征消失。因此,研究如何去除图像斑点噪声对SAR图像有效应用具有重要意义[1-2]。近十几年来,小波变换作为一种强有力的统计信号处理工具,被引入到去除SAR图像斑点噪声算法中[3-4]。
以往小波变换斑点噪声抑制算法,有的仅考虑了小波系数之间的幅度相关性,有的未考虑小波系数之间的相关性[5-6]。然而,小波系数不仅具有幅度间的相关性,而且其符号间也具有强相关性[7],即小波系数如果在粗的分解级中为正(或为负),则在细的分解级中也为正(或为负)。小波系数符号之间的相关性,在图像边缘附近表现更为明显,因此将各尺度小波系数之间的这种符号相关性引入到现有小波去斑算法中,可提高滤波器及小波斑抑制算法的性能[9]。在考虑小波系数在幅度、符号的相关性的基础上,提出一种新的小波斑抑制算法,以更好区分小波系数中哪些需保留,哪些需抑制,从而在抑制SAR图像斑点噪声时,保持图像边缘细节特性。
1 小波系数之间符号相关性
为说明利用小波系数符号相关性对更好抑制斑点噪声的作用,以一个典型的Blocks带乘积噪声信号及其小波分解系数(见图1)为例进行说明。此处采用UDWT(平稳离散小波变换)[10]。由图1(c)和图1(e)可见,图1(e)中的系数更接近图1(d)中干净信号的小波系数。所以,利用图1(e)中的小波系数比利用图1(c)中的小波系数更易检测出重要需保留系数和非重要需抑制系数,从而使信号的突变部分更好保持。

图1 Blocks信号及其小波系数Fig.1 Blocks signal and its wavelet coefficients
2 本文算法
本文通过引入小波系数符号之间的相关性,提出了一个新的小波去斑算法。小波系数幅度之间的相关如图2所示,其包括尺度间相关和尺度内相关。

图2 尺度间和尺度内小波系数幅度相关Fig.2 Amplitude inter-correlation and inner-correlation for wavelet coefficients
假设g=f×u为1幅2维的SAR斑点噪声图像,其中:f为不含噪声部分的干净图像;u为乘积斑点噪声,与f不相关,则通过对数变换,将乘积斑图像转换为加性噪声图像模型。图像模型表示为
G=F+V
(1)
式中:G,F,V分别对应lgg,lgf,lgu。
将对数变换后的图像通过2维UDWT变换,变换尺度为J+1。LHj(n), HLj(n), HHj(n) 分别表示j尺度下3个不同的细节子图像,LLj(n)为相应的近似子图像。
为利用小波系数符号之间的相关性,产生一系列新系数,为
(2)
式中:j=0,1,…,J;sgn()为符号函数;k分别对应LH,HL和HH 3个不同的子图像,k=1,2,3。
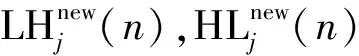
对于处理每个小波系数n,都会取1个以此像素为中心的邻域窗口(模板)Bj,k(n)。由于不同的细节子图像获取的图像细节特征不同,因此所取的Bj,k(n)也应有所不同。3个面积为3×3的邻域窗口如图3所示。图中:3个窗口分别对应3个不同类型的子图像,阴影部分的像素参与计算。

图3 三个3×3邻域窗口Fig.3 Three 3×3 neighborhood windows
在邻域窗内,利用尺度内各系数的幅度相关,得到公式为
(3)
式中:N为Bj,k的大小。利用尺度间小波系数幅度间的相关性可得
(4)
根据系数收缩准则,对系数进行收缩处理,表示为
LHj(n)=
(5)
HLj(n)=
(6)
HHj(n)=
(7)
式中:λLHj,λHLj和λHHj为3个门限值;LHj(n),HLj(n),HHj(n)为经过收缩后的新系数值。DONOHO[3]给出了1个简单的门限计算,即
(8)
式中:σ为斑点噪声标准差,表示为
σ=median(|HH1(n)|)/0.674 5
(9)
估计上述的3个门限值,公式为
(10)
本文首先对SAR图像进行平稳小波变换;接着在小波变换域内综合考虑尺度内和尺度间小波系数符号和幅度的相关性,采用相应的系数收缩准则,然后对各细节子图像的小波系数进行收缩处理,得到收缩后的小波系数,最后进行逆变换,得到去除斑点噪声后的图像。
计算步骤如下:
1) 对图像进行对数变换,并利用2维的UDWT 进行尺度为J+1的小波分解。
2) 根据式(2)考虑小波系数符号间的相关产生一系列新系数。
3) 根据式(3)和(4),考虑尺度间和尺度内小波系数幅度间的相关性。
4) 利用式(10)估计3个门限值。
5) 根据步骤4)得到的门限值,遵照式(5)、式(6)和式(7)的收缩规则,对各细节子图像的小波系数进行收缩处理,得到收缩后的系数。
6) 利用收缩后的小波系数进行逆小波分解,均值校正[11]。
7) 进行指数变换,得到去除斑点噪声的图像。
3 实验结果
为验证本算法的有效性,主要利用合成斑点噪声图像数据和真实SAR图像数据进行实验。将本算法处理后的结果和软阈值门限法[3]处理后的结果相比较。
根据乘积斑噪声模型从光学图像(见图4(a))中合成模拟的斑点噪声图像(见图4(b))。图4(c)和图4(d)分别为利用软阈值门限法和本文算法处理后的去斑图像。

图4 对合成斑图像的滤波实验Fig.4 Despeckling experiment for simulated speckled image

图5 对真实SAR图像的滤波实验Fig.5 Despeckling experiment for real SAR image
选取1幅真实的SAR图像(见图5(a)),该图像中包含了许多结构细节特征。图5(b)和图5(c)分别为软阈值门限法和本文算法对该SAR图像处理后的去斑图像。滤波性能主要从斑点噪声抑制程度和图像边缘保持两方面来评估,主要由ENL(等效视数)、EPI(边缘保持指数)[12]和η(边缘保持因子)[13]表示。其中:ENL是用来评估斑噪声抑制程度的指数,ENL越小表示斑点噪声抑制程度越大;EPI和η是用来评估图像边缘保持效果的指数,它们的值越大表示边缘保持越好。合成斑点噪声图像和真实SAR图像的去斑效果评估指数见表1,表2。由表可知:与软阈值门限法相比,本文算法在斑点噪声抑制程度和衡量细节保持方面均有所改善。

表1 合成斑点噪声图像去斑效果主要评估指数
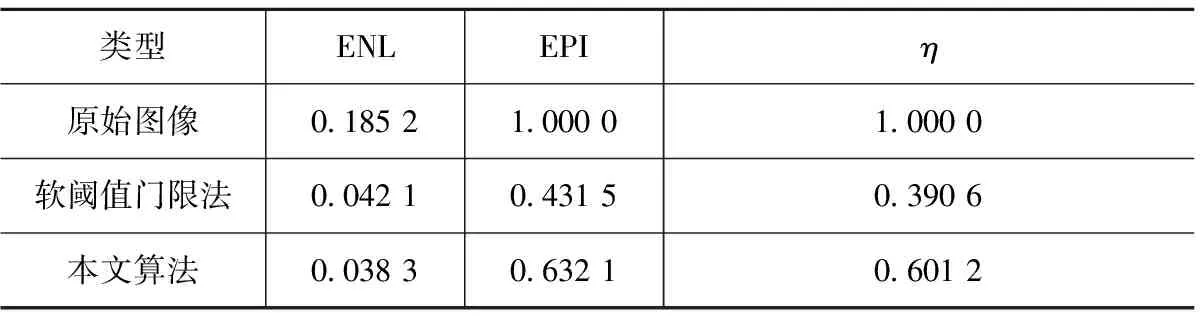
表2 真实SAR图像去斑效果主要评估指数
4 结束语
SAR图像小波分解后的小波系数符号之间存在强烈的相关性,本文将这种相关性引入到小波斑点噪声抑制算法中,提出了一种新的小波斑点噪声抑制算法。该算法充分考虑了小波系数幅度和符号之间的相关性。利用合成斑点噪声图像和真实SAR图像数据进行实验验证,与软阈值门限法的实验结果相比较。结果表明:本文算法在斑点噪声抑制程度、图像边缘保持上与软阈值门限法相比有了较大改进。本文对提高SAR图像辐射分辨率提供了一种有效的斑点噪声抑制方法,有助于提高SAR图像的应用水平。
[1] ULABY F, KOUYATE F, BRISCO B, et al. Textural infornation in SAR Images [J]. IEEE Transactions on Geoscience and Remote Sensing, 1986, 24(2): 235-245.
[2] RANEY R K, WESSELS G J. Spatial considerations in SAR speckle consideration [J]. IEEE Transactions on Geoscience and Remote Sensing, 1988, 26(5): 666-672.
[3] DONOHO D L. De-noising by soft-thresholding [J]. IEEE Transactions on Information Theory, 1995, 41(3): 613-627.
[4] 毛成林, 万寿红, 岳丽华, 等. 一种基于双树复小波变换的SAR图像边缘检测算法[J]. 中国科学院大学学报, 2014, 31(2): 238-242.
[5] CAI Z, CHENG T H, LU C, et al. Efficient wavelet-based image denoising algorithm[J]. Electronics Letters, 2001, 37(11): 683.
[6] CHEN G, LIU X. Wavelet-based despeckling SAR images using neighbouring wavelet coefficients [C]// IEEE International Geoscience and Remote Sensing Symposium. IEEE, 2005: 1764-1766.
[7] LU R, XING M, ZHENG B, et al. Adaptive despeckling SAR images based on scale space correlation [C]// IEEE International Conference on Acoustics, Speech, and Signal Processing, 2005. Proceedings. IEEE, 2005:ii/1013-ii/1016.
[8] BORRAN M J, NOWAK R D. Wavelet-based denoising using hidden Markov models [C]// IEEE International Conference on Acoustics, Speech, and Signal Processing, 2001. Proceedings. IEEE, 2001:3925-3928.
[9] CHANG S G, YU B, VETTERLI M. Spatially adaptive wavelet thresholding with context modeling for image denoising[J]. IEEE Trans Image Process, 2000, 9(9): 1522-1531.
[10] ARGENTI F, ALPARONE L. Speckle removal from SAR images in the undecimated wavelet domain [J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(11): 2363-2374.
[11] XIE H, PIERCE L E, ULABY F T. Statistical properties of logarithmically transformed speckle[J]. IEEE Trans. Geosci. Remote Sensing, 2002, 40(3): 721-727.
[12] HAN C, GUO H, WANG C. Edge preservation evaluation of digital speckle filters[C]// Geoscience and Remote Sensing Symposium, 2002. IEEE, 2002:2471-2473.
[13] YAN Y, ZHOU Y, LI C S. Quantitative assessment of speckle filters for SAR images [J]. Second International Conference on Image and Graphics, 2002: 428-433.
