能源平衡模型中工作模式判别方法

李 立，朱 野，陈 雨，张晓杰

(上海微小卫星工程中心，上海 201203)

0 引言

能源分系统是人造卫星的重要组成部分，为卫星各分系统的设备提供安全可靠的能源供给，是卫星必不可少的重要保障系统[1-2]。在卫星能源设计阶段，需要用能源平衡模型计算卫星能源消耗情况以确保卫星能源分系统能满足整星需求[3-6]，并确保卫星能源能满足载荷任务的顺利执行和卫星的健康运行。另外，由于星上能源有限，由地面或星上自主规划任务的卫星也需要利用能源平衡模型对规划的任务进行能源约束，防止星上能源出现不能支持任务完成的情况[7-10]。

当能源平衡模型用于指导电源设计及对卫星任务进行规划时，能源约束计算在地面执行，以确定任务能源消耗并决定任务是否上注。对于自主规划任务的卫星，能源约束计算在星上执行，用以决定任务是否要执行。能源约束计算依据卫星的工作模式，结合每个工作模式下的能源功耗计算能源消耗情况，其重点在于准确获取卫星在某时间段的工作模式。目前，工作模式判别时采取只考虑载荷工作期间的能源消耗以简化计算过程[11-12]，或者在仿真期间预先人工确定卫星工作模式作为输入[13-15]。非载荷单机功耗对能源影响较大时，只考虑卫星载荷的消耗会使能源平衡计算不准确。人工判别的方法需要人为干预，对多任务且姿态需要相应机动的卫星，多个任务和充电条件相互影响，姿态调整错综复杂，计算量大且易出错，只适用于工作模式简单的卫星。

为此，本文提出一种通过建立索引表及数据库查询的方式判别卫星工作模式的方法，该方法考虑了卫星光照条件、姿态调整策略以及载荷任务规划，保证了能源平衡计算的准确性，并在工程上可用软件实现。该方法首先综合卫星轨道时间序列和地面的规划任务时间序列信息，结合卫星姿态调整规则，判别不同时间序列工作状态下的卫星工作模式并建立索引表，再查阅某时刻数据库中各个时间序列的工作状态，结合索引表可得到此时整星工作模式。该方法操作简便，确定好每种卫星工作序列下的工作模式后建立索引表，可通过查表确定卫星工作模式，并可根据实际需要添加时间序列对工作模式进行约束，具有一定通用性和可扩展性。

1 卫星能源平衡模型

卫星能源平衡模型计算未来一定时间内卫星的能源消耗情况，用以评估执行一定任务状态下卫星能源能否充放电平衡，能源平衡模型原理如图1所示。

卫星能源平衡模型进行卫星能源消耗计算的流程为：获取卫星轨道时间信息和规划任务时间信息，综合判别卫星在某段时间内的卫星工作模式；获取卫星工作模式后，由卫星单机功耗列表可知当前工作模式下的整星功耗，根据时间间隔可计算出该段时间内的能源消耗情况；对时间进行累加后按照上述步骤继续计算，可得到整个仿真周期内的能源消耗情况，在仿真结束后，输出能源平衡计算结果。

在能源平衡模型中，关键在于正确判别某段时间内卫星的工作模式，以获取卫星的功耗。工作模式的准确判别直接影响卫星功耗的计算准确性。对于多任务且姿态需要根据任务进行机动的卫星，多个任务相互影响，还需要考虑卫星的轨道信息和姿态调整规则，卫星工作模式判别较为复杂。

2 卫星工作模式判别

对于多任务且姿态需要根据任务进行机动的卫星，其工作模式与卫星轨道信息、规划任务时间信息、姿态调整策略有关。卫星轨道信息决定卫星是否处于光照区，是否具备充电条件。规划任务和姿态调整策略确定卫星姿态和使能的载荷单机，决定卫星是否具备充电条件以及当前整星功耗大小。本文提出的卫星工作模式判别方法需要先综合轨道时间信息、规划任务时间信息，并考虑姿态调整策略得到卫星工作模式索引表，再将上述时间序列注入数据库，查询某时刻各时间序列的工作状态，由索引表得到整星工作模式。

2.1 时间序列工作状态

卫星时间序列包含轨道信息时间序列和规划任务时间序列。本文以低轨倾斜圆轨道，且姿态需要根据任务进行机动的卫星为例进行建模。卫星在轨运行且无异常情况时，可分为待命状态和任务状态。

在无任务需求时，卫星处于待命状态，只考虑轨道信息时间序列。卫星在光照区姿态为对日定向，以进行能源获取；在阴影区为对地定向，以维持卫星稳定运行。对地与对日切换需要执行姿态机动，由对日定向转为对地定向发生在卫星进入阴影后tmin，由对地定向转为对日定向发生在卫星出阴影前tmin。待机状态下轨道时间序列卫星工作状态如图2所示。卫星在待机状态下的工作状态有：对日充电状态、对地待机状态和姿态机动状态。

图2 轨道时间序列工作状态图Fig.2 Working state diagram of satellite orbit time series

当卫星需要执行任务时，进入卫星工作状态，考虑规划任务时间序列。本文建模的卫星有两个独立的载荷任务，都需要在执行任务期间维持对地定向。单独考虑载荷任务，在载荷任务开始前和结束后都需要执行姿态机动。载荷任务2还需要在任务开始前和结束后执行k(k>t)min的任务处理。载荷任务1和载荷任务2单独工作的工作状态如图3、4所示。载荷1工作状态有：姿态机动状态、对地载荷任务1状态、空闲状态。载荷2工作状态有：任务处理状态、姿态机动+任务处理状态、对地载荷任务2状态、空闲状态。

图3 载荷任务1工作状态图Fig.3 Working state diagram of payload 1

2.2 工作模式索引表

图4 载荷任务2工作状态图Fig.4 Working state diagram of payload 2

2.1节给出了待机和工作状态下的工作状态图。轨道信息时间表、载荷任务1时间表和载荷任务2时间表相互影响，整星工作模式由这3个时间序列共同确定。

由图2～ 4可见，卫星执行姿态机动的时机有6处，分别为进阴影时、出阴影时、执行载荷任务1前、执行载荷任务1后、执行载荷任务2前、执行载荷任务2后。姿态机动在下一步需要的姿态与当前姿态不符时才执行，其满足约束如下：

1) 进阴影时。当前正在执行的载荷任务已处于对地定向，不执行对地姿态机动。

2) 出阴影时。当前还有未执行的载荷任务，不执行对日姿态机动。

3) 执行载荷任务1前。当前阴影区为对地定向或在执行载荷任务2，不执行对地姿态机动。

4) 执行载荷任务1后。当前阴影区为对地定向或在执行载荷任务2，需要继续保持对地定向，不执行对日姿态机动。

5) 执行载荷任务2前。当前阴影区为对地定向或在执行载荷任务1，不执行对地姿态机动。

6) 执行载荷任务2后。当前阴影区为对地定向或在执行载荷任务1，需要继续保持对地定向，不执行对日姿态机动。

通过不同时间序列的工作状态，可得到所有时间序列工作状态组合下的工作模式，并建立二者对应关系的索引表。其建立过程如图5所示。

图5 工作模式判别示意图Fig.5 Schematic diagram of working pattern discrimination

对于图5中的时间点1，轨道时间序列为对日充电状态，载荷任务1序列为对地姿态机动，载荷任务2序列为空闲状态，则载荷任务1的姿态机动需要执行，综合工作模式为姿态机动。对于图5中的时间点3，轨道时间序列为对地姿态机动，载荷1序列为载荷1任务状态，载荷2序列为任务处理状态，由于载荷1序列处于对地状态，则轨道时间序列中的对地姿态机动不执行，最终的工作模式为载荷1任务+任务处理。同理，时间点2的工作模式为载荷1任务，时间点4、5为载荷1任务+任务处理，时间点6为载荷任务2模式。

3个时间序列的工作状态有限，其中，轨道时间序列工作状态有4个，分别为：对日充电、对地姿态机动、对地待机、对日姿态机动。载荷1工作状态有4个，分别为：对地姿态机动、对地载荷任务1、对日姿态机动、空闲。载荷2工作状态有6个，分别为：任务处理1、任务处理1+对地姿态机动、对地载荷任务2、对日姿态机动+任务处理2、任务处理2、空闲，上述6个姿态机动因为卫星的姿态不同可能不需要执行。3个时间序列可以通过穷举的方式判别卫星的工作模式，总共有4×4×6=96种工作状态组合，以此建立工作模式索引表。各个工作状态符号表示见表1。

表1 工作状态符号表示

工作模式索引表见表2，考虑篇幅只列出部分项。分别从轨道时间序列、载荷任务1序列和载荷任务2序列中得到各自的工作状态，对应表2中的“组合”项；判别出卫星在该状态下的整星工作模式，对应表2中的“模式”项。“模式”项中，由于6个姿态机动功耗一样，在“模式”一栏中姿态机动统一用P表示，载荷2的任务处理功耗一致，统一用T表示。

表2 工作模式索引表

2.3 工作模式查询

建立各时间序列工作状态与工作模式的索引表后，只需要知道某时刻各时间序列的工作状态，就能从索引表中查询到整星工作模式。为实现快速查询，可借助数据库的排序查询功能。其操作流程为：建立3个数据库表分别存储轨道时间序列、载荷任务1时间序列和载荷任务2时间序列各工作状态的起始时间、结束时间、工作状态；运用数据库查询语句得到某时刻3个数据库表中的工作状态，得到表2中的“组合”项，则对应的“模式”项即为整星工作模式；时间累加，继续进行上述查询步骤，可得到整个仿真周期内卫星的工作模式。

3 算法优化

3.1 索引表优化

前文给出了根据各时间序列工作状态确定卫星工作模式的过程。对于表2，需要从3个数据表中分别获取工作状态，比较3次以后得到综合工作模式，操作繁多。为此，工程实现时为3个序列中每个工作状态赋值，数据库查询后求得3个序列状态值的和，通过建立状态值和与工作模式对应关系索引表，只需要判别1次即可。工作状态赋值需要满足一个状态值和只对应一个综合工作模式。在本文建立的能源平衡模型中，状态值设定见表3，根据表2和表3得到状态值和与卫星工作模式对应表见表4。当从3个数据库表中获取到某一时刻3个序列的状态值和之后，可以从表4中得到当前卫星的工作模式。

表3 状态值设定

表4 状态值和与卫星工作模式索引表

3.2 计算加速

3.2.1 步进加速

能源平衡模型以初始时间累加步进时间模拟星上时间，步进时间长度决定了模型的计算量和仿真精度。步进时间长度过小，则相同时间段内需要查询次数多，计算量大；步进时间长度过大，则可能导致工作模式判别过于粗糙，影响计算精度，对步进长度的选择需要在计算量和计算精度上进行权衡。

为平衡计算量和计算精度，步进长度随着工作模式变化而变化，以最大计算误差小于设定的允许计算误差为原则。即在卫星消耗较低的工作模式下，步进长度可适当放大，在能源消耗较高的工作模式下，则缩小步进长度。例如，设定允许最大计算误差为能源满时的0.1%，当步进长度为N时，最大误差时间为(N-1)s。设步进长度缺省值为6，若当前为功耗最大的载荷1工作，其每秒功耗相当于满能源的0.02%，则N=(0.1/0.02)+1，即步进长度设定为6；若当前为功耗较低的待机模式，其每秒功耗相当于满能源的0.004%，则N=(0.1/0.004)+1，即步进长度设定为26。软件具体实现方式为：查询当前卫星工作模式后，根据当前工作模式功耗计算出下一次步进长度。为防止由低功耗模式转为高功耗模式时过大的步进长度增大误差，当检测到当前模式功耗大于上次功耗模式时，计算时间点退回到上次时间点并以缺省步进长度重新计算至当前时间点。

3.2.2 查询加速

卫星一种工作模式持续几分钟甚至几十分钟，只利用步进时间来获取工作模式会耗费大量计算时间。本文提出一种步进时间和查询时间共同工作的方式来进行计算加速。设定计算最大误差为e，当前时间为t1，能量值为v1，步进长度为h，查询长度为m(m≥0)。查询t1+h时的工作模式及功耗p1和t1+h+m时的工作模式及功耗p2。若二者工作模式相等，时间更新为t2=t1+h+m，能源更新为v2=v1-p2(h+m)，h更新为(e/p2)+1。否则，时间更新为t2=t1+h，能源更新为v2=v1-p1h，h更新为(e/p1)+1，并在t1+h至t1+h+m的时间范围内不进行模式是否相等的查询。

当卫星某种工作模式持续时间较短时，查询时间过大会使查询时间点跳过该工作模式段，没有起到加速效果，并可能导致跳过某些时间较短的任务段计算。查询时间过短，则加速效果不明显。步进长度的选取与卫星具体时间序列有关。为此，通过仿真计算确定如何针对具体的卫星任务特征选取查询长度。设最大计算误差为满电量的0.1%用于步进长度更新，并模拟了卫星执行载荷任务的时间段，仿真参数见表5。

表5 仿真参数

卫星光照时间约每隔2 h有40 min的光照时间。卫星姿态需满足第2.2节的6个约束。查询步长为0～240 s，以20 s为间隔进行组合，记录对24 h的轨道时间序列和载荷任务时间序列进行处理的计算时间，每个查询步长下测量3次取平均值，其结果如图6所示。

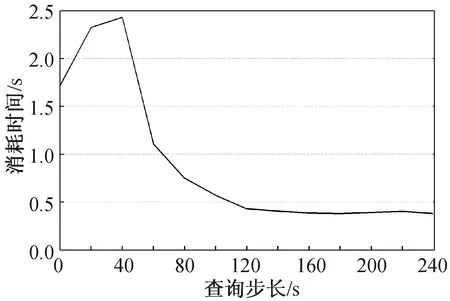
图6 不同查询步长下的计算时间Fig.6 Computing time versus query length

从图6看出，过小的查询长度步进不能起到加速效果，还会由于频繁查询导致计算时间变长。在该仿真任务类型中，随着查询步长增加，能源消耗计算所耗费时间呈减小趋势，在查询步长大于120 s后，消耗时间减少的能力有限，同时考虑到该模型中载荷任务2任务处理时间为3 min，过大的查询长度可能导致短时间的工作模式遗漏，故取120 s作为查询步长。

4 结束语

针对工作模式复杂的卫星能源平衡模型，提出了利用索引表和数据库查询确定工作模式的方法。该方法通过穷举方式建立时间序列工作状态和卫星工作模式的索引表，再查询时间序列数据库并参照索引表得到卫星工作模式。考虑了卫星的光照、姿态调整、载荷工作序列等因素，并根据实际需要添加时间序列对工作模式进行约束。该方法使卫星能源平衡计算更为准确，工程上利用数据库进行软件实现使工作模式判别能自主运行，有利于卫星的长期能源管理。该方法适用于工作模式判别较为复杂的卫星。然而，通过不同时间序列组合判断卫星工作模式，随着卫星时间序列约束的增加，其组合数会相应增大，从而使建立索引表的工作量过大。针对这种时间序列约束过多的情形，人工穷举的方式工作量庞大，可建立额外的模型，根据约束自动建立索引表克服该问题，并需要研究更为快速的查询方法弥补多次查询的时间开销。

[1] 闫蕾. 卫星电源测试评估系统的初步研究[D]. 北京：中国科学院研究生院(空间科学与应用研究中心), 2004.

[2] REMY F, BROSSIER C, MINSTER J F. Intensity of satellite radar-altimeter return power over continental ice: A potential measurement of katabatic wind Intensity [J]. Journal of Glaciology, 2017, 36(123): 133-142.

[3] WU J, CHENG Y, SRIVASTAVA A K, et al. Hardware in the loop test for power system modeling and simulation [C]// Pes Power Systems Conference and Exposition. IEEE, 2006: 1892-1897.

[4] 王涛，黄晓，郗志伟. 低轨道微小卫星电源系统研究[J]. 电源技术, 2012, 36(7)： 1011-1014.

[5] 鄢婉. 太阳同步轨道卫星电源系统设计计算方法研究[J]. 中国空间科学技术, 2001, 21(2)： 22-28.

[6] JARVENTAUSTA P, REPO S, RAUTIAINEN A, et al. Smart grid power system control in distributed generation environment [J]. Annual Reviews in Control, 2010, 34(2): 277-286.

[7] 王万玉，张志强. 多站多星任务调度模型及求解[J]. 电讯技术， 2011, 51(4)： 1-6.

[8] 陈英武，方炎申，李菊芳，等. 卫星任务调度问题的约束规划模型[J]. 国防科技大学学报, 2006, 28(5)： 126-132.

[9] 乔亦实, 田景峰, 李劲冬,等. 一种遥感卫星能源平衡约束分析系统及方法: 201610609295.1 [P]. 2017-01-11.

[10] LEE S, JUNG W C, KIM J. Task scheduling algorithm for the communication, ocean, and meteorological satellite [J]. ETRI Journal, 2008, 30(1)： 1-12.

[11] 高黎, 沙基昌. 基于合同网的分布式卫星系统任务优化分配研究[J]. 宇航学报, 2009, 30(2)： 815-820.

[12] 于海. 对地观测卫星成像调度与约束修正方法研究[D]. 长沙：国防科学技术大学, 2007.

[13] 崔文聪, 林宝军, 吕从. 近地卫星电源系统能量的仿真分析[J]. 计算机仿真, 2005, 22(8)： 35-36，44.

[14] 李小飞, 乔明, 陈琦. 倾斜轨道卫星能量平衡优化分析方法[J]. 航天器工程, 2014, 23(4)： 52-56.

[15] BIHL T, HEIDENREICH J, ALLEN D, et al. Specttra:a space power system modeling and simulation tool [C]// International Energy Conversion Engineering Conference. Colorado: AIAA, 2009： 1-14.