不同工况下的缸盖低周疲劳对比分析

张应兵，路明

（安徽江淮汽车集团股份有限公司，安徽 合肥 230601）

前言

缸盖作为发动机的核心零部件承受着复杂的载荷，随着近年来排放和油耗法规的升级，发动机的热效率逐步提升，缸盖的工作环境则进一步恶化，在高温环境中，缸盖材料的机械性能会有明显的下降。在高低温交替变化，同时又承受循环的机械载荷，缸盖的燃烧室部分很容易发生低周疲劳失效。目前对于车用发动机的缸盖低周疲劳问题研究较少，之前的研究一般针对稳态温度场下的疲劳寿命分析。但根据雨流计数法，中间工况的选择对于疲劳结果有很大的影响，本文将基于sehitoglu低周疲劳分析理论，研究稳态工况和瞬态工况下的某发动机的缸盖低周疲劳问题，对比两种工况下的低周疲劳寿命。

1 低周疲劳分析理论

根据sehitoglu损伤理论，总损伤为机械损伤（Dfat）、氧化损伤（Dox）以及蠕变损伤（Dcreep）之和，如式1所示。

机械损伤模型基于Coffin-Manson公式：

其中为剪切应变，E为弹性模量， 为泊松比，为疲劳强度系数，b为疲劳强度指数，为疲劳延展性系数，c为疲劳延展性指数，为机械损伤寿命。

氧化损伤模型为：

其中hcr为临界裂纹长度，δo为氧化物延展性，B、β为材料常量，α为应变率敏感性常量，Kpeff为有效氧化常量，为氧化应变，为氧化寿命，为氧化相位，。

蠕变损伤模型为：

其中 A、m为材料常量，K近似为屈服强度，α1、α2为比例因子，为活化能，为蠕变相位，。[1-7]

2 有限元模型

低周疲劳分析需要考虑装配载荷以及温度载荷，依据此模型包括缸体、缸盖、缸盖螺栓、气门座圈、气门导管以及缸垫。有限元模型如图1所示，为了减少计算时间，缸盖低周疲劳开裂一般发生在燃烧室位置，因此，在燃烧室位置需要划分较细密的网格，且在倒角位置要划分直角三角形的网格，保证计算精度，燃烧室位置的局部网格模型如图2所示。

图1 有限元模型

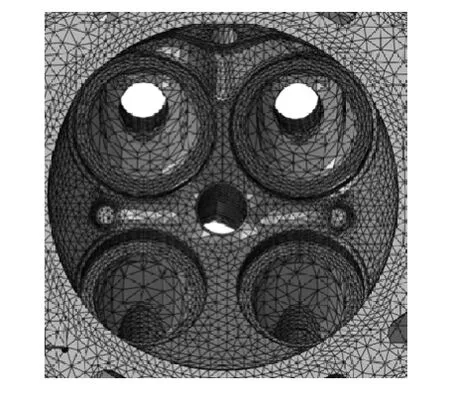
图2 燃烧室局部网格

3 低周疲劳分析温度边界

分析时同时考虑稳态温度场以及瞬态温度场两种工况，稳态温度场考虑怠速工况及全速全负荷工况，中间的过程结果按照线性插值得到，而瞬态分析工况如图3所示，温度场分析共分为五个循环，初始循环从室温到全速全负荷工况，再到怠速工况，每个循环持续360秒，中间过程考虑实际温度变化，稳态工况以及瞬态工况最后一个循环的全速全负荷温度场如图4、5所示，中间点的温度场由于篇幅的原因不贴出，从结果可以看出，两种工况的温度分布略有不同，瞬态工况最高温度较稳态工况低4℃。

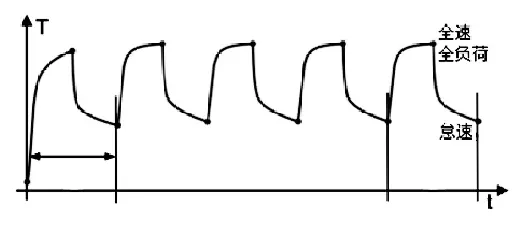
图3 瞬态温度场分析工况

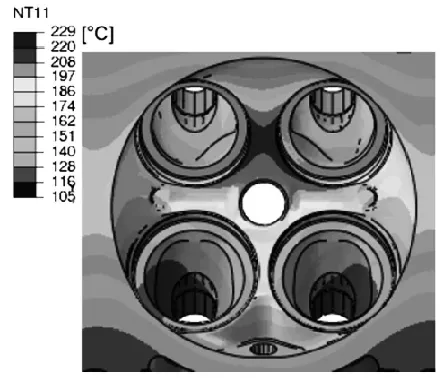
图4 稳态工况温度分布

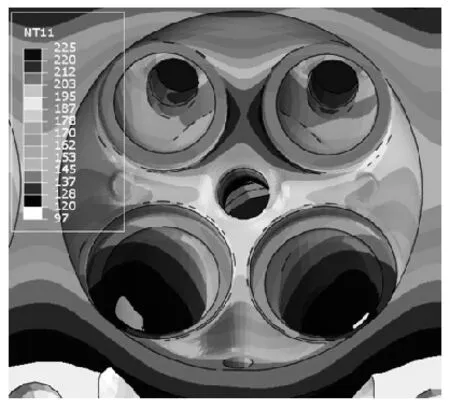
图5 瞬态工况温度分布

4 低周疲劳分析对比

考虑稳态温度场下的低周循环工况如图6所示，分析中一个疲劳循环工况持续360s，一个工况包括四个过程，从怠速到全速持续90s，保持全速90s，降低到怠速90s，保持怠速 90s，中间过程温度场为线性插值。由于考虑材料的塑性和蠕变等特性，开始几个疲劳循环中各节点中的应力和应变并不稳定，而在最后的疲劳分析中我们需要稳定的应力应变结果，因此分析又分为三个阶段，初始循环阶段包括两个疲劳工况，然后持续30小时，目的是使蠕变特性表现出来，最后稳定循环阶段包括两个疲劳循环工况，最后一个循环用于疲劳分析。

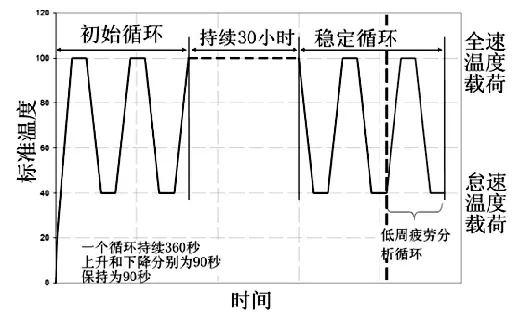
图6 稳态低周疲劳循环工况

考虑瞬态温度场下的低周循环工况如图7所示，一个循环工况同样持续360s，与稳态不同的是，中间工况点考虑瞬态的温度场分析结果。

图7 瞬态低周疲劳循环工况

根据两种不同工况的结果进行低周疲劳分析后，疲劳寿命结果如图8、9所示，从结果可以看出，稳态工况下的最低寿命为7473，而瞬态工况下的最低寿命为1589，瞬态工况下的结果远低于稳态工况，从安全系数的分布情况也可以看出，瞬态工况下的低周疲劳寿命更加危险。

图8 稳态工况低周疲劳寿命分布

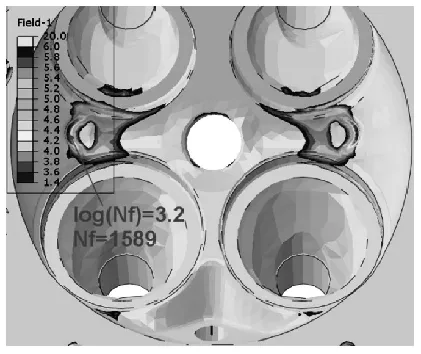
图9 瞬态工况低周 疲劳寿命分布

5 结论

1）本文基于稳态及瞬态两种工况对某发动机缸盖进行低周疲劳分析，从结果看，两种工况的疲劳结果分布基本一致，最小寿命位置均在进排气门之间。

2）稳态工况最低寿命为 7473，瞬态工况最低寿命为1589，瞬态工况远低于稳态工况，表明瞬态工况更加苛刻。

[1] Surech,S.Fatigue of Materials[M].国防工业出版社,1993,389-404.

[2] 聂宏.Miner公式和 Manson-Coffin公式的能量基础[J].航空学报,1993,14（5）:310-312.

[3] 赵帅帅,陈永祥等.基于修正 Coffin-Manson模型的加速寿命试验设计与评估[J].强度与环境,2013,40（4）:52-58.

[4] HU YanDong,HU ZhiZhong,CAO ShuZhen.Theoretical study on Manson-Coffin equation for physically short cracks and lifetime prediction[J].SCIENCE CHINA Technological Sciences,2012,55（1）:34-42.

[5] 胡延东,胡志忠,曹淑珍.物理短裂纹 Manson-Coffin公式的理论研究及寿命预测[J].中国科学:技术科学,2012,42（3）:272-281.

[6] 郭乙木,陈朝东,张仪萍.室温Manson-Coffin公式的一种修正[J].浙江大学学报,1998,32（6）:671-677.

[7] 杨俊,谢寿生,祁圣英等.基于等效应变的轮盘低循环疲劳寿命预测[J].空军工程大学学报,2010,11（6）:12-16.

[8] 新矢伸昭.铸铁气缸盖低循环寿命预测方法的开发[J].国外内燃机,2003,（5）:52-56.

[9] 朱小平,刘震涛,俞小莉.热-机耦合条件下气缸盖强度及疲劳寿命分析[J].机电工程,2011,28（10）:1176-1179.

[10] 刘勤,姬广振,侯新荣等.热固耦合条件下气缸盖结构可靠性设计分析[J].车用发动机,2011,（5）:68-71.

[11] 邓帮林,刘敬平,杨靖等.某缸盖热机疲劳分析[J].湖南大学学报,2012,39（2）:30-34.

[12] 胡定云,陈泽忠,温世杰等.某柴油机气缸盖疲劳的可靠性预测[J].车用发动机,2008,（176）:38-40.