基于EKF的电动方程式赛车动力电池容量试验研究

刘峰云，谭子胡，李学博，高奇

（长安大学汽车学院，陕西 西安 710064）

引言

电池作为电动赛车的核心之一，影响着电动赛车的动力性、经济性以及续驶里程。目前对于电动汽车动力系统匹配方面的研究[1][2][3][4]，并未考虑电池容量与整车质量的关系，缺乏电池容量方面的优化。因此，如何设计并优化电池容量，是本文主要考虑的问题。

本文以动力性、续驶里程设能量消耗效率为主要设计目标，基于比赛工况，对长安大学某型号纯电动方程式赛车电池参数进行匹配设计。由于目前阻容网络建立的简单动态电池模型[5]过于简化，其不能够良好的体现电池的非线性电动势、温度和电流影响下的容量变化等特性。所以本文考虑温度和电流对电池容量的影响因素，基于等效电路模型应用Simulink建立电池动态模型，基于EKF对电池容量进行仿真和放电试验对比分析，确定最优化电池容量。

1 电池设计

1.1 电池类型的选择

为了保证赛车顺利完成耐久动态项目，电池必须提供足够的能量。电池单体个数越多，则所能提供的能量越多，但同时电池质量增加，而电池作为赛车上占重比达 20%～25%的重要部件，其质量极大影响着赛车各项动力性能。直线加速赛方面，电池又必须具有高放电倍率。与其它类型电池比较，锂离子电池在比能量和比功率方面具有优异的表现，同时良好的充放电效率，且在高低温条件下性能良好[6]。

1.2 电池参数设计

本文电池参数设计主要包括总能量和单体电池数量两部分。首先计算出完成耐久赛所需总能量。电动方程式赛车以最大加速度行驶消耗的功率（忽略坡度阻力消耗功率）[7][8]为：

式中：du/dt为最大加速度。

基于往年比赛工况，即各时刻赛车车速和加速度（忽略坡度阻力消耗功率），可求得各时刻电机功率Pw由式（2）可求得电动方程式赛车完成耐久赛电机消耗总能量[9]E1：

考虑到电机和电机控制器效率、电池放电效率以及电池放电深度[9]，电池所需总能量为：

式中：ηm为电机和电机控制器效率；ηb为电池放电效率；k为电池放电深度，k=0.9。耐久赛是FSEC各赛中消耗能量最多的一项赛事，所以最终确定电池能量不得低于E2。计算电池单体数量时，主要考虑电机工作电压和电池最大放电电流，以保证电机稳定功率输出，并且符合FSE电机功率输出要求。根据所选用电池单体标称电压Un、最高电压Um和电机控制器工作电压，所以可求得电池单体数量N。

2 电池动态模型

目前工程应用上最常用的电池模型是等效电路模型。电池模型确立之后，其内部参数会随着工作电流、放电状态(SOD)、温度、循环寿命和自放电等因素的影响而变化。基于FSEC比赛实际情况，本文主要考虑电流、温度这两个对电池容量产生影响的因素。

本文电池模型选用戴维南等效电路模型[10][11][12]，其动态特性如图1所示。R1描述电池欧姆电阻，R2和C1组成的RC支路描述电池极化效应。UOCV作为电池开路电压，与电池放电状态SOD（4）的关系：

SOD(t)由式（5）计算得到：

图1 等效电路模型

图2 电池脉冲放电特性

图3 电池1C放电特性

图4 电池20℃放电特性

参考温度(20℃)和参考放电倍率(1C)脉冲放电曲线如图2所示。脉冲电流加载瞬间，欧姆内阻引起电池电压变化，根据式（6）可得到欧姆电阻初始值：

图5 温度影响因子

根据△U3，采用最小二乘拟合法得到R2、C1的初始值和。不同温度及不同电流条件下关系曲线如图 3-4所示。k1和分k2别作为温度和电流对SOD(t)的影响因子[13]：

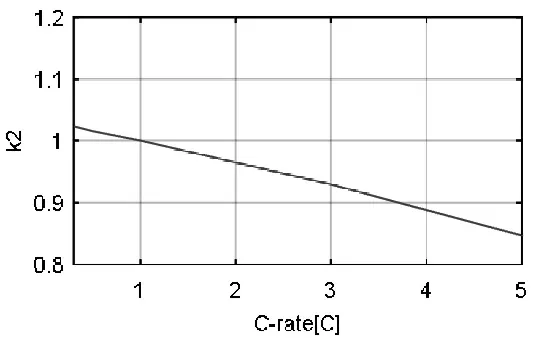
图6 电流影响因子

影响因子k1和k2由不同温度、电流下的终态SODf与参考温度、电流下的终态SODf的比值得到[14]，如图5-6所示。同时，不同温度、SOD状态下的R1、R2和C1也会随之变化。可得到温度和SOD对R1、R2和C1的影响因子[14]分别为k3、k4、k5、k6、k7、k8。根据电池工作温度、工作电流对SOD(t)的影响因子，以及温度和SOD(t)对R1、R2和C1的影响因子建立电池动态模型。

3 电池容量优化及试验验证

本文主要以耐久赛以及效率赛为目标设计电池，即要求在耐久赛瞬时功率高、时间长等极端环境下，电池依旧能够稳定可靠、安全的输出功率，并保证具备足够的能量以完成比赛。

3.1 EKF估计电池SOC

对于离散非线性系统：

式（8-9）分别为系统的状态方程和观测方程，均为非线性传递函数，同时 wk、vk为互不想关的系统噪声，Rw、Qv分别为它们的方差。xk为系统状态，yk为系统输出，uk为系统输入。

f(xk, uk)、g(xk, uk)由一阶泰勒展开线性化，并令

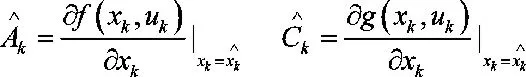
第一步：初始化k=0，给定、协方差矩阵P0和噪声方差Rw和Qv的初值。

第二步：首先预测系统当前状态值、输出和误差协方差，然后利用测量得到的物理系统输出更正状态预测和误差协方差。循环递推计算如式（10-14）：

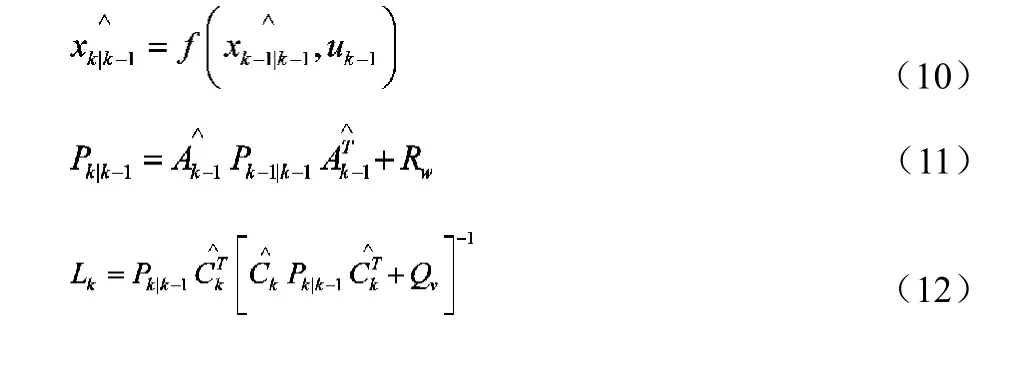
式中：k=1,2,3,…。

在使用EKF估计电池SOC时，SOC作为电池系统的一个状态变量，电流i作为系统的输入，电池工作电压U作为系统的输出。

系统状态方程为：

式中：T—采样周期

—采样k时刻R2上的电压估计值

τ1—RC环节时间常数

输出观测方程为：

式中：UOCV(SOCk)表示电池OCV与SOC存在的对应关系，通过式(4)得到。

3.2 基于比赛工况仿真优化

基于Simulink分别建立不同单体数量的电池动态模型，并利用比赛工况基于 EKF进行动力性仿真。仿真结果如图7-8所示。

图7 工况下电池电压仿真特性

图8 工况下电池SOC仿真特性

当电池单体数量达到N及以上，耐久赛结束时电池能够提供电机控制器稳定的工作电压；随着单体数量的增加，整车质量也相应增加，单圈时间相应的也就越长。所以本文选择N单体电池组，既保证顺利完成耐久赛，同时减轻整车质量，减少耐久赛用时，达到提高比赛成绩的目的。图 12-13表明当耐久赛结束时，电池组能够保证稳定可靠、安全的输出电机所需功率，同时电池剩余 SOC为 15%，满足本文耐久赛结束时电池剩余SOC高于10%的设计要求。

3.3 试验验证

试验环境温度为20℃。首先将电池充满至截止电压，静置后用新威尔电池充放电试验柜及电池组进行模拟比赛工况放电试验，试验过程中自动记录电池端电压及放电电流。持续放电至放电截止电压，利用安时计量法[15]计算电池放电容量并得到电池 SOC。放电试验现场图及结果图如图 9-11所示。

试验结果表明，在耐久赛时间段内，电池能够稳定安全的满足比赛需求，同时电池剩余 SOC为 14%，与仿真结果基本相符，仅相差1%SOC，验证了该电池容量的合理性。

4 结论

图9 电池放电试验现场图

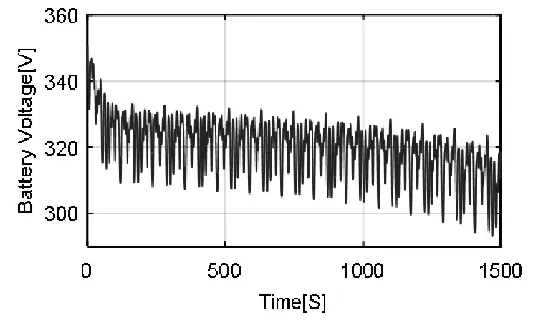
图10 电池放电试验电压特性

图11 工况下电池SOC试验与仿真

本文以FSEC比赛为背景，提出了一种基于EKF的电池容量优化方法。根据比赛要求，以动力性和续驶里程为主要设计目标，完成电动方程式赛车电池参数设计。通过对选用的单体锂离子电池进行不同条件下的放电试验，在Simulink中建立温度-电流影响的电池动态模型，并进行比赛工况下的仿真与试验对比。结果表明，本文所建立的电池动态模型能够满足试验分析要求，基于EKF建立以SOC为参考目标的方法也完成了蓄电池质量-电量的优化。

[1] 刘灵芝,张炳力,汤仁礼.某型纯电动汽车动力系统参数匹配研究［J］.合肥工业大学报,2007,30( 5):591-593.

[2] 查鸿山,宗志坚,刘忠途,伍庆龙.纯电动汽车动力匹配计算与仿真[J].中山大学学报（自然科学版）,2010,49(5):47-51.

[3] 吴发亮,阳林,邓仲卿,周永光.FSE赛车动力性参数的设计仿真与验证[J].公路与汽运,2013,（3）:6-9.

[4] 姜立标,吴斌,冯骁,杨彦哲.电动汽车动力性参数的仿真设计与试验验证[J].汽车工程,2011,33（12）:1013-1017.

[5] V. H. Johnson, A. A. Pesaran, and T. Sack, “Temperature-dependent battery models for high-power lithium-ion batteries,” Battery Ther-mal Manag. Assessment, 2002.

[6] M. Stanley Whittingham. History, Evolution, and Future Status of Energy Storage[J]. Proceedings of the IEEE, 2012,100:1518-1534.

[7] 余志生.汽车理论[M].北京:机械工业出版社,2009

[8] Wang Lifang,Xu Huiwen. Dynamic Match and Optimizing Design of Electric Vehicle Powertrain[J]. IEEE, 1999,1:387-390.

[9] Zhenpo Wang, Wenliang Zhang. Battery system matching and design for a formula student electric racecar[J]. Transportation Electrifi cation Asia-Pacific, 2014:1-6.

[10] Michalczuk M, Grzesiak L.M, and Ufnalski B. A lithium battery and ultracapacitor hybrid energy source for an urban electric vehicle[J].Przeglad Elektrotechniczny (Electrical Review), 2012,88(4b):158–162.

[11] Rahmoun A, Biechl H. Modelling of Li-ion batteries using equival-ent circuit diagrams[J]. Przeglad Elektrotechniczny (Electrical Review), 2012,88(7b):152-156.

[12] Chulsung P, Jinfeng L, and Chou P.H. B#: a battery emulator and power-profiling instrument[J]. IEEE Design & Test of Computers,2005,22(2):150-159.

[13] Lijun Gao, Shengyi Liu, Roger A. Dougal. Dynamic Lithium-ion Battery Model for System Simulation[J].IEEE Transactions of Components and Packaging Technologies, 2002,25(3):495-505.

[14] Marek MICHALCZUK, Bartłomiej UFNALSKI, Lech M. GRZE SIAK, Piotr RUMNIAK. Power converter-based electrochemical battery emulator[J]. Przeglad Elektrotechniczny(Electrical Review),2014,18-22.

[15] Yanhui Zhang, Wenji Song, Shili Lin, Ziping Feng. A novel model of the initial state of charge estimation for LiFePO4 batteries[J].Journal of Power Sources, 2014,248:1028-1033.