完美信息的期望价值理论及其在医药经济学评价和决策中的应用

陶立波

（中山大学药学院 广州 510006）

在传统的医药经济学评价中，由于现实条件约束，通常是采用抽样调查、文献研究等方法来得到参数的平均水平，然后据此建立经济学模型开展评价并支持相关决策[1]。基于平均数的分析和决策，其实会掩盖很多问题并导致不公平，因为个体间有差异，不同的参数取值会导致不同的取舍结果。因此，如果能获得个体水平的“完美”信息，从而可针对具体情况进行差异化决策，就可以比基于平均数的决策获得更优结果。这是信息所能带来的价值，也即是“完美信息的期望价值（Expect Value of Perfect Information，EVPI）”理论[2]的基本思想。

EVPI理论在工程建设、环境保护等领域已有长期的应用[3]，在近几十年间被引入到卫生决策领域，并在西方国家获得推广。但该理论方法在我国的传播和应用还很少。本文将对EVPI理论的基本思想及其在医药经济学评价中的应用方法进行概括性阐述，以帮助我国研究者和决策者了解该理论并在工作中加以探索和应用。

1 基于平均数进行决策的弊端

基于统计学理论，平均数是表征一组数据的集中趋势的常用指标[4]。采用平均数进行分析和决策是常用的方法，例如在一项医药经济学评价中，分别计算医药技术A与B应用于一组患者后的平均成本和平均健康效果，从而计算平均水平上的增量成本效果比：（平均成本A-平均成本B）/（平均效果A-平均效果B），来支持决策。

但是，由于个体差异，这组患者中不同个体的最优医药技术可能是不同的：某些人可能适宜采用A，另一些人更适宜采用B。无论基于平均水平选择了A或是B，都只是对一部分人正确，而对另一部分人错误，从而导致不公平和社会损失。

因此，这促使人们思考：如果能获得完全的信息，了解每个个体的适宜选择，那就可以进行个体化决策并在整体上达到最优效果，其价值显然会高于基于平均数的决策结果。

2 EVPI基础理论

完美信息的期望价值理论的基本含义，就是完整详细地掌握每个个体的具体信息，从而在决策中为每个个体量身定制适宜的方案，以获得最优结果[2]。在医药经济学评价中就可以理解为：掌握每一位患者及其每一种可能的疾病发生发展路径，对每位患者的每种可能路径的卫生成本和健康产出进行科学的估算，从而为每位患者均选择最适宜的医药技术。如此，每个个体都获得最优结果，其总和就是整体最优结果，相比基于平均数的决策结果，就会有更高的社会价值。这个价值的增量，就是获取完美信息所能产生的期望价值。

EV PI理论可以作如下公式表达：假定有K个医药技术进行评价，其目标人群有N人，NB表示净收益（在医药经济学中通常采用“增量效果×成本效果比临界值-增量成本”来计算）。基于平均水平进行评价的方法为：Max（Average(NB，K，N)），即对于N人群选择K个技术中平均净收益最大者。基于EVPI的评价方式则为：Average（Max(NB，K，N)），即对于N人群中的每个人都选择K个技术中净收益最大者，然后取其平均数。EVPI就是两者的差值：Average（Max(NB，K，N)）- Max（Average(NB，K，N)）。

以下以一个简单的医药经济学评价虚拟案例来对EVPI进行说明。假定要对医药技术A和B进行经济学评价，目标人群共有3人，每个人经A和B治疗后的成本(万元)和效果(QALY)如表1所示。从结果来看，根据每个患者的成本和效果，第1、3号患者的最优策略是A（因为其增量成本效果比为5万/QALY，低于5.5万/QALY的界值），而第2号患者的最优策略是B。然而，基于全部患者的平均成本和效果进行计算，得到增量成本效果比是7.7万/QALY，高于界值，因此最终评价结论是拒绝A而选择B。显然，这对于第1、3号患者都是错误的决策，他们因此错过了性价比更高的医药技术A。

在这个虚拟案例中，如果因为信息有限或计算能力不足而基于平均数进行决策，最终会选择B应用于整个群体：其平均成本20万，平均健康效果为7.7个QALY。但如果获得了完美的信息，就可以让第1、3号患者使用A，而让第2个患者使用B，这样得到的平均成本是27万、平均健康效果是9个QALY。人均多花7万而多获得1.3个QALY，增量成本效果比为5.3万/QALY（低于界值，具有经济性），而其净收益为1.3QALY×5.5万/QALY -7万 = 0.15万。这就是完美信息的价值，即：相比平均数决策，基于完美信息进行个体化最优决策，在临界值5.5万/QALY的情况下，能为群体增加0.15万的额外收益。

3 EVPI的局部分析

上述的EVPI是对所有个体的所有可能性进行全面掌握后（即完美信息）所能获取的额外价值。这可以看作是增加信息能够获取的额外收益的上限，因为已经穷尽了所有可能的个体变化信息。在具体研究和决策中，还可以对EVPI中不同的部分进行细分，从而可获得不同方面的信息、解决不同的问题。这其中比较常用的是参数信息的期望价值（Expect Value of Perfect Information for Parameters，EVPPI）和抽样信息的期望价值（Expect Value of Sample Information，EVSI）。

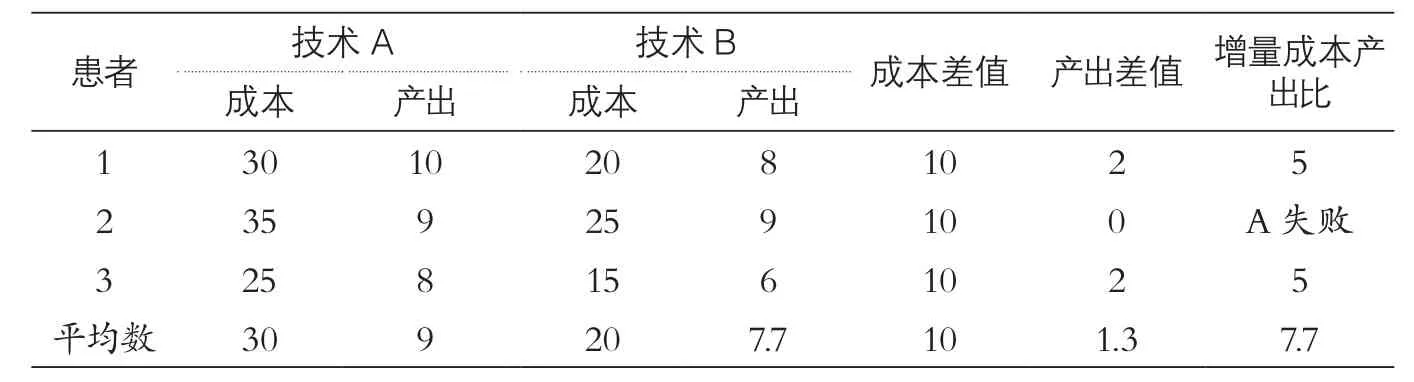
表1 医药技术A与B进行比较的医药经济学评价

EVPPI是指获得了研究中某一个或某一组参数的完美信息所得到的期望价值。在信息不充分时，人们会选择参数的某一个值（通常为平均数）进入分析和计算，得到的是该参数值水平下的结果。而在完美信息的情境下，可以对该参数所有可能的取值进行分析，获取在不同取值下的适宜选择，从而达到最优结果。类似于EVPI，EVPPI的公式表达为：EVPPI=Average（Max(NB，K，P)）-Max（Average(NB，K，P)）（其中P为参数值的集合），此处EVPPI的含义即为：不同参数值下K个技术中净收益最大者的均数，减去不同参数值下K个技术中净收益平均数最大者。

需要指出的是，EVPPI分析一般不推荐仅对单个参数开展，而是应该选择有关联的一组参数。例如，研究中各种卫生成本、各个状态下的健康效用，或患者的各种基线情况等。推荐成组分析EVPPI的原因，一方面是变量间有关联，应该一起分析；一方面是开展某个研究可以同时得到一组参数的情况，从而可以对不同研究的优先度进行分析，例如，开展成本研究可以得到一组成本参数信息，而开展健康效用调查可以得到一组健康效用值，通过分别计算成本参数组和效用参数组的EVPPI及其开展研究的成本，就可以判断哪个研究的成本和收益更佳，从而决定哪个研究应该优先开展。

EVSI是指对所需参数进行抽样研究所能得到信息的价值，例如开展一项临床研究所得到的疗效和安全性的价值。EVSI分析可探讨不同样本量所对应的价值：如果样本量较小，则其能体现的参数变化较少，因而样本信息的价值（即EVSI）也就较小；当样本量足够大时，参数的所有变化都能获得体现，此时EVSI就是所研究参数的EVPPI。所以说，随着抽样研究的样本量增加，EVSI也会不断增加，其上限就是对应参数的EVPPI。另一方面，样本量增加会导致研究的成本也增加，当研究成本超过收益（EVSI）时就意味着开展该研究是“不经济”的。基于这样的方法，就可以从经济学角度来探讨抽样研究的最佳样本含量。

基于上述EVPI理论的思想，还可以对不同方面的信息价值进行分析，例如探讨不同研究设计或不同对象人群的信息价值，从而可从经济学角度来帮助决策：研究是否值得开展，何种研究设计更合理，等等。具体的技术方法请参见相关文献和著作[5-7]。

4 总结与讨论

在传统的研究和决策方法中，通常是采用人群平均水平来开展分析，但EVPI理论提示我们，如果能掌握个体的完美信息、从而为每个个体选择适宜的决策，就能获得最优的结果。这事实上和“精准医疗”的思想是完全一致的，即应该为不同的个体量身定做适宜的医疗卫生方案以追求最优结果，这也是医疗卫生事业未来的发展方向。

基于EVPI理论的思想，在医药经济学评价及其相关的卫生、医保决策中，也不应该满足于仅根据人群平均水平进行评估和决策，而是应该尽可能获取信息、分析信息，为社会民众提供差异化乃至个性化的医疗服务和管理方案，从而追求社会获益的最大化。在卫生大数据的积累和分析能力不断提高的今天，事实上这方面的技术难度正在快速降低，更主要的困难可能会来自制度和管理方面。此外，EVPI理论也为相关的研究管理提供了启示，因为它可以提示不同研究方向、不同研究设计方法的期望价值，结合开展研究的所需成本，就可以对研究设计和方案选择进行更精细化的管理。

完美信息的期望价值理论在欧美国家的卫生体系中已有多年的应用，例如英国NICE就曾对不同卫生技术评估及相关的参数研究项目进行过分析，以探讨不同研究设计的期望价值和经济性[8]。我国这方面的探索和应用还较少，在全社会对卫生和医保的管理水平提出越来越高期望的今天，我们有必要对这方面的理论和技术进行深入的学习、研究和应用。

[1]中国药物经济学评价指南课题组，刘国恩，胡善联，等. 中国药物经济学评价指南(2011版)[J]. 中国药物经济学 ,2011(03):6-9.

[2]Briggs A, Claxton K, Sculpher M. Decision modelling for health economic evaluation[M].Oxford University Press,2006.

[3]Thompson M K, Evans J S. The value of improved national exposure information for perchloroethylene (perc): a case study for dry cleaners[J]. Risk Anal,1997(17):253-271.

[4]丁元林，王彤 . 卫生统计学 (第 2 版 )[M]. 北京:科学出版社,2017,434.

[5]Wilson E C, Mugford M, Barton G, et al.Efficient Research Design: Using Value-of-Information Analysis to Estimate the Optimal Mix of Top-down and Bottom-up Costing Approaches in an Economic Evaluation alongside a Clinical Trial[J]. Med Decis Making,2016,36(3):335-348.

[6]Claxton K P, Sculpher M J. Using value of information analysis to prioritise health research:some lessons from recent UK experience[J]. Phar macoeconomics,2006,24(11):1055-1068.

[7]Tuffaha H W, Reynolds H, Gordon L G, et al.Value of information analysis optimizing future trial design from a pilot study on catheter securement devices[J]. Clin Trials,2014,11(6):648-656.

[8]Claxton K, Eggington S, Ginnelly L, et al.A Pilot Study of Value of Information Analysis to Support Research Recommendations for NICE[M]. London:National Institute for Health and Care Excellence (NICE),2005.