共振梁法测量材料阻尼适用性的理论与试验研究

屈忠鹏, 盛美萍(西北工业大学 航海学院,西安 710072)

阻尼技术可在较宽频带内有效控制结构振动，因此广泛应用于飞行器、船舶和汽车等领域[1-2]。应用阻尼技术的关键前提是准确评估材料的阻尼性能，这主要依赖于试验测量，常用的测量方法有动刚度法、共振梁法等[3～5]。

共振梁法使用非接触式激振和拾振，可减小附加阻尼的影响。对于可自支撑的材料，直接使用单层梁进行测量，精度较高[6]。对于不能自支撑的材料，如粘弹性材料，则必须与可自支撑的材料组成复合梁进行测量，进而反演得到阻尼层材料的阻尼特性。测量标准[7-8]中的经典反演公式忽略了基底层阻尼，但未明确说明忽略基底层阻尼可能导致的影响，所以研究人员常会对经典公式的适用性感到疑惑，并且难以估计测量结果的精度。胡卫强[9]推导了一个方程组，对基底层阻尼的影响进行了简单讨论，但因方程组较为复杂，没能对误差的产生机理和影响因素进行系统分析。另一种计入基底层阻尼的方法是复模量计算[10]，这种方法不能显式表达阻尼层的损耗因子，所以也不适合用来分析基底层阻尼的影响。

本文基于复刚度法，得到了经典公式误差的理论表达式，通过数值仿真定量分析了阻尼比、模量比和厚度比等主要影响因素对误差的影响规律，从而明确了经典公式的适用范围。并分别使用钢和有机玻璃作为基底梁，测量了聚氨酯橡胶的损耗因子，对理论分析的结果进行了验证。

1 理论

图1为共振梁法试验试件的示意图。

(a) 基底梁

(b) 复合梁图1 试验试件Fig.1 Experimental specimens

试验中分别测量基底梁和复合梁的振动特性，根据两者的差异，即可反演得到阻尼层的材料参数。根据材料力学的定义，可得基底梁和复合梁的弯曲刚度分别为

(1)

(2)

式中：B1和Bc表示基底梁和复合梁的弯曲刚度；E1和E2表示基底层与阻尼层的杨氏模量；H1和H2表示基底层与阻尼层的厚度。两式相除可得复合梁与基底梁的弯曲刚度比为

(3)

式中：e和h表示阻尼层与基底层的模量比与厚度比。为考虑材料阻尼的影响，用ηc、η1和η2分别表示复合梁、基底层和阻尼层的损耗因子，那么式(3)可改写为

(4)

针对式(4)，若忽略基底层损耗因子η1，可得到阻尼层损耗因子的经典反演公式

(5)

为计入基底层阻尼的影响，仅忽略式(4)小括号(·)项内的高阶小量

(6)

(7)

将其代入式(4)，并分离实部和虚部，可得阻尼层损耗因子的修正反演公式

(8)

将式(5)与式(8)相减，可得到经典公式的误差函数

(9)

其中κ=η2/η1表示阻尼层与基底层的损耗因子比，α=Bc/B1表示复合梁与基底梁的弯曲刚度比，其值由式(3)决定。因ehα<<1，若忽略其影响，则误差函数化简为

(10)

2 仿真分析

为确定经典公式的适用范围，首先分析其误差的变化规律。由式(9)和式(10)可知，误差由阻尼层与基底层的损耗因子比κ、模量比e和厚度比h共同决定。

图2为误差随三个参数的变化曲线。图中横轴为损耗因子比κ，纵轴为百分比误差，连续曲线根据式(9)计算得到，离散点为式(10)近似计算的结果。图(a)中固定厚度比h为2，由图可见误差百分比与损耗因子比κ呈反比例关系，并且模量比e越小，误差越大。图(b)中固定模量比e为10-3，由图可见厚度比h越小，误差越大。由此可知，相比于基底层，阻尼层的损耗因子、模量和厚度越小，经典公式误差越大，可达到甚至超过100%。但当损耗因子比κ、模量比e和厚度比h这三个参数任意变化时，其组合方式较多，据此不易界定经典公式的适用范围。

对比图2中的连续曲线和离散点，可见式(9)和式(10)的结果几乎完全一致，由此可知，小量ehα可以忽略，那么模量比e和厚度比h的影响可由复合梁与基底梁的弯曲刚度比α这一个参数来反映。考虑到弯曲刚度比α是试验中应首先获得的参数之一，以下将使用弯曲刚度比α作为参数来界定经典公式的适用范围。注意这里损耗因子比κ、模量比e和厚度比h均指阻尼层与基底层之间的比值，而弯曲刚度比α是指复合梁与基底梁弯曲刚度之间的比值。

图3为误差随弯曲刚度比α的变化规律。可见弯曲刚度比α越小，经典公式的误差越大。当弯曲刚度比α接近1时，误差急剧增大。当弯曲刚度比α不变时，损耗因子比κ越小，误差越大。

(a) 固定厚度比h=2

(b) 固定模量比e=10-3图2 经典公式误差随各参数变化规律Fig.2 Classic formula errors for different parameters

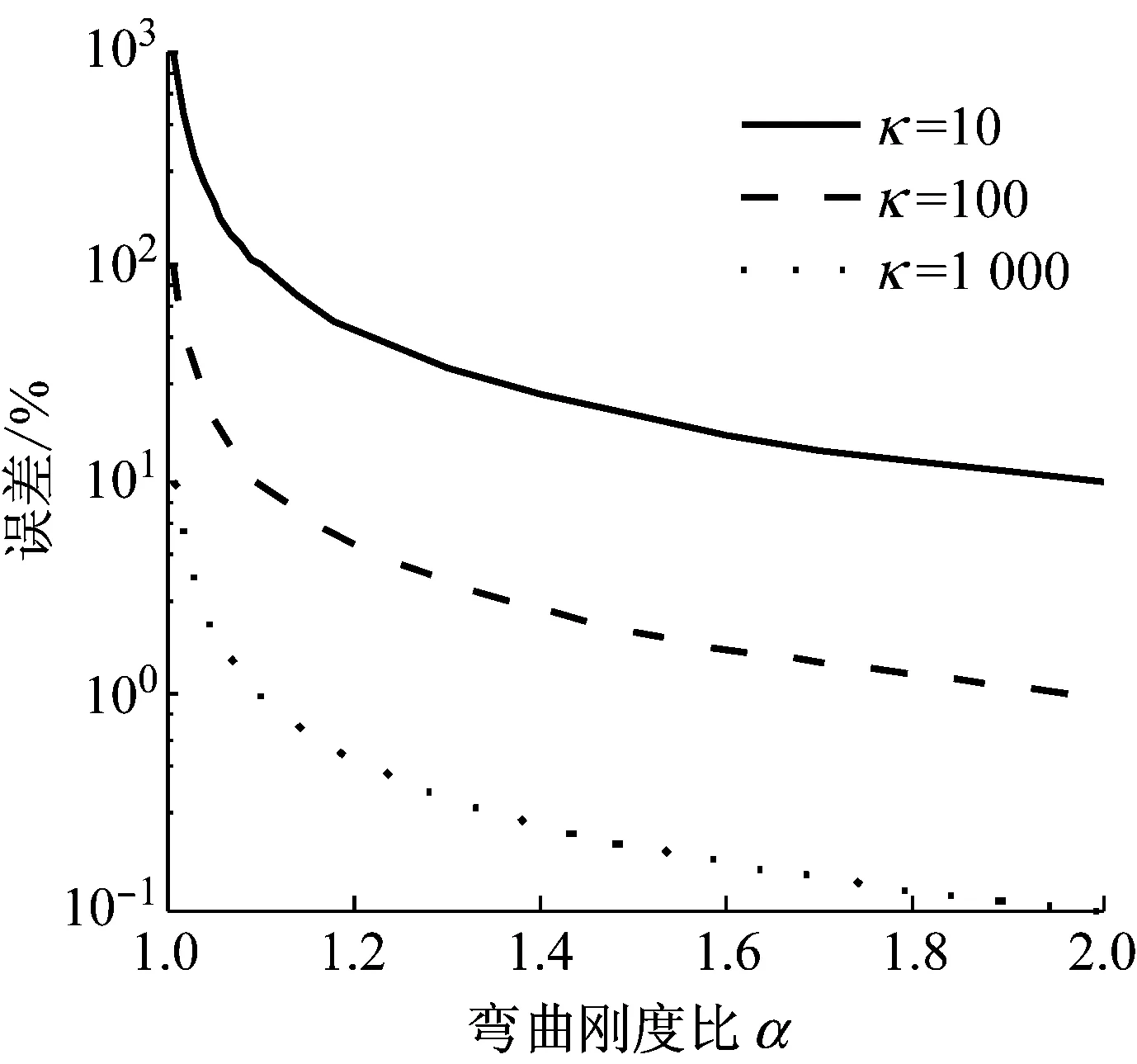
图3 经典公式误差随弯曲刚度比变化规律Fig.3 Classic formula errors varying with stiffness ratio

一般情况下，阻尼层损耗因子大于基底层损耗因子，其损耗因子比κ介于1～1 000；将阻尼层粘贴于基底梁后，所形成复合梁的刚度将略大于基底梁刚度，其弯曲刚度比α介于1～2。以下分析该区域内经典公式的适用性。

图4中横轴和纵轴分别为弯曲刚度比α和损耗因子比κ，粗实线表示经典公式的10%误差线。右上阴影区误差更小，左下空白区误差更大。可见对于弯曲刚度比α和损耗因子比κ较大的情况，误差很小，经典公式适用；反之则不适用。表1中列出了不同损耗因子比条件下，误差小于10%时对试件弯曲刚度比最小值的要求，这些值可用来界定经典公式的适用范围。

图4 经典公式10%误差线Fig.4 10% error line for the classic formula

表1 经典公式适用范围界定表Tab.1 Parameters to confine the classic formula

为更直接的指导测量，对照表1，分别针对钢和有机玻璃两种典型的基底层进行讨论。

(1)钢基底的损耗因子约为0.001。若阻尼层为橡胶等阻尼材料，其损耗因子一般大于0.1，那么损耗因子比大于100，对照表1，可知只要弯曲刚度比大于1.1，基底层阻尼影响即可忽略，经典公式适用。但若所测材料损耗因子较小、或试件弯曲刚度比较小，为减小误差，最好考虑基底层阻尼的影响。

(2)有机玻璃基底的损耗因子约为0.06。一般而言，阻尼层材料的损耗因子不超过1，那么损耗因子比为10左右或更小，为保证经典公式精度，需要弯曲刚度比超过2。这将使得复合梁阻尼过大，导致试件振动幅度过小，使得测量无法进行。因此，对于有机玻璃基底，一般应考虑基底层阻尼的影响。

3 试验验证

为对分析结果进行验证，分别使用钢和有机玻璃作为基底梁，对聚氨酯橡胶的损耗因子进行了测量。试件的形状如图1所示。按照测量标准，为方便夹持，将试件的一端制成阶梯状。将阻尼材料粘贴在基底梁的一边，制成自由阻尼复合梁试件。对于钢基底复合梁试件，基底层和阻尼层的厚度分别为1.0 mm和4.2 mm，其密度分别为7 725 kg/m3和1 128 kg/m3，试件有效长度(不含阶梯)为240 mm。对于有机玻璃基底复合梁试件，基底层和阻尼层的厚度分别为1.7 mm和2.1 mm，其密度分别为1 206 kg/m3和1 128 kg/m3，试件有效长度(不含阶梯)为225 mm。图5为试验系统的示意图。将试件的阶梯端进行夹持，使之呈悬臂梁状态。使用非接触式电磁激振器对试件产生白噪声稳态激励，同时使用非接触式电涡流传感器采集试件的振动位移信号。对所采数据进行FFT分析即可得到试件的频率响应曲线。

图6为试验测得两组试件的频响曲线。从中可直接识别出基底梁和复合梁的模态频率，使用半功率带宽法可识别出不同模态的损耗因子。两组试件模态频率和损耗因子值分别如表2和表3所示。因受电磁激振器附加刚度的影响，第一阶模态频率的结果可能产生较大误差，所以仅对第二～四阶模态频率的结果进行了计算。

图5 试验系统示意图Fig.5 The experimental system diagram

(a) 基底梁为钢

(b) 基底梁为有机玻璃图6 两组试件的速度频响曲线Fig.6 Velocity frequency response of the specimens

表2 钢基底梁和复合梁的模态频率及损耗因子Tab.2 Mode frequency and loss factor of steel base and composite specimens

表3 有机玻璃基底梁和复合梁的模态频率及损耗因子Tab.3 Mode frequency and loss factor of PMMA base and composite specimens

进而使用标准中的经典公式和本文计入基底阻尼的修正公式分别对阻尼层的损耗因子进行了反演，其结果如图7所示。

图7 两种基底测量聚氨酯橡胶的损耗因子

Fig.7 Loss factor of polyurethane rubber measured by two group of specimens

图7中实线表示经典公式的结果，虚线表示本文修正公式的结果。由图可见，对于钢基底试件，经典公式与修正公式仅有很小差别，忽略基底层阻尼影响不大。这是因为聚氨酯橡胶损耗因子大于0.1，并且试件的弯曲刚度比大于1.1，满足第二部分所得误差小于10%的条件。对于有机玻璃基底试件，经典公式的结果明显高于修正公式的结果，基底层阻尼不能忽略。计入基底层阻尼的影响后，两组试件的结果较为一致。

为进一步验证本文所得结论，分别列出了两组试件复合梁与基底梁的弯曲刚度比和阻尼层与基底层的损耗因子比，如表4所示。由表中可见，两组试件的弯曲刚度比和损耗因子比随模态阶数升高均有所增大。由表4数据，根据式(10)可估算忽略基底阻尼导致的误差，并与根据图7计算得到的实际误差比较，结果如图8所示。

表4试件各阶模态的弯曲刚度比和损耗因子比

Tab.4Stiffnessratioandlossfactorratioofdifferentmodesofthespecimens

钢复合梁有机玻璃复合梁第二阶第三阶第四阶第二阶第三阶第四阶弯曲刚度比1．111．141．161．241．281．32损耗因子比3915008745．037．649．14

图8为误差函数估计误差与测量实际误差的比较。可见两者几乎完全重合。此外，因为随着模态阶数升高，弯曲刚度比和损耗因子比均有所增大，所以高阶模态的误差较低阶模态更小，这与本文理论分析所得结论是一致的。

图8 经典公式两种基底测量聚氨酯橡胶损耗因子的误差

Fig.8 Loss factor errors of polyurethane rubber calculated by the classic formula

4 结 论

针对自由阻尼梁结构，推导了经典公式误差的理论表达式，基于此对基底层阻尼的影响进行了系统分析，进而明确了经典公式的适用范围。研究表明：

(1) 阻尼层与基底层的损耗因子比、模量比和厚度比越小，误差越大。

(2) 模量比和厚度比的影响可由复合梁与基底梁的弯曲刚度比反映，并且弯曲刚度比越小，误差越大。

(3) 对于钢基底，若阻尼层损耗因子大于0.1，且试件弯曲刚度比大于1.1，基底层阻尼可以忽略；对于有机玻璃基底，基底层阻尼不能忽略。

参 考 文 献

[1] JONES D I G. Handbook of viscoelastic vibration damping[M]. New York: Wiley, 2001.

[2] 黄志诚, 秦朝烨, 褚福磊. 附加粘弹阻尼层的薄壁构件振动问题研究综述[J]. 振动与冲击, 2014, 33(7): 105-113.

HUANG Zhicheng, QIN Zhaoye, CHU Fulei. A review about vibration problems of thin-walled structures with viscoelastic damping layer[J]. Journal of Vibration and Shock, 2014, 33(7): 105-113.

[3] 侯宏，余虎，孙亮. 基于共振法的黏弹性细棒力学参数宽频测试[J]. 振动与冲击, 2015, 34(9): 107-110.

HOU Hong, YU Hu, SUN Liang. Determination of dyanmic parameters of viscoelastic thin bar using resonance measurement method under pulse excitation[J]. Journal of Vibration and Shock, 2015, 34(9): 107-110.

[4] 王超, 吕振华. 黏弹性阻尼材料力学参数测试实验用双边附加自由结构阻尼试件设计方法研究[J]. 振动与冲击, 2014, 33(5): 102-108.

WANG Chao, LÜ Zhenhua. Research on the design of specimens damped both sides used in the measurement of viscoelastic material’s mechanical parameters[J]. Journal of Vibration and Shock, 2014, 33(5): 101-108.

[5] OYADIJI S O, TOMLINSON G R. Characterization of the dynamic properties of viscoelastic elements by the direct stiffness and master curve methodologies, part 1: design of load frame and fixtures[J]. Journal of Sound and Vibration, 1995, 186(4): 623-647.

[6] KORUK H, SANLITURK K Y. Identification and removal of adverse effects of non-contact electromagnetic excitation in Oberst beam test method[J]. Mechanical Systems and Signal Processing, 2012, 30: 274-295.

[7] Standard test method for measuring vibration-damping properties of materials: ASTM E756-04[S]. American Society for Testing and Materials, 2010.

[8] 声学材料阻尼性能的弯曲共振测试方法:GB/T 16406[S]. 北京:国家技术监督局,1996.

[9] 胡卫强. 阻尼材料动态性能宽频带测量关键技术研究[D]. 西安:西北工业大学, 2009: 17-19.

[10] LIAO Y, WELLS V. Estimation of complex Young’s modulus of non-stiff materials using a modified Oberst beam technique[J]. Journal of Sound and Vibration, 2008, 316(1): 87-100.