新型聚焦反共振式主减隔振系统性能分析

沈安澜， 刘续兴， 陈 静， 张鹏杰(中国直升机设计研究所，江西 景德镇 333001)

直升机从其研制成功之后就以其机动灵活、垂直起降、不受场地限制等特点在军事以及民用各个领域使用广泛。直升机独有的工作特性和结构形式使得直升机振动问题一直是制约直升机发展过程中的一个重要问题。振动问题直接影响机载设备的寿命、结构的可靠性以及乘员的驾乘舒适性。引起直升机振动问题的一个主要原因是旋翼，旋翼作为直升机一个最主要振源其产生的动载荷通过主减及其支撑结构传递到机身。为了降低直升机的振动水平，各国的直升机工程师采取了多种减振措施，主减隔振技术作为其中一种有效减振措施，其主要思路是将旋翼通过主减速器传递到机体的动载荷降低到最小，达到降低全机的振动水平的目的[1-2]。

1 聚焦反共振式主减隔振系统建模

1.1 动力反共振隔振器

动力反共振隔振器在常规的弹簧/阻尼隔振装置上附加惯性元件。这类隔振器将隔振与吸振巧妙的结合起来，形成具有反共振隔振特征与隔振特点的隔振器，在某个特定的频率上，附加的惯性元件产生的惯性力能够完全抵消振源向被隔振物体传递的动载荷。其最大的特点在于，理论上在无阻尼情况下传递率可以为零，即使在有阻尼的情况下传递率也很小。动力反共振隔振器原理和力学模型，如图1所示[3-5]。

1.2 聚焦反共振式主减隔振系统

聚焦式主减隔振系统主减采用聚焦弹性方法固定于机体上，即主减撑杆延长线聚焦于一点(虚焦点),主减底部通过弹性支撑与机体连接，主减/旋翼系统垂向的频率较高而绕虚焦点的摆动频率较低，从而在保证主减/旋翼系统垂向刚度的同时减小旋翼旋转平面内激励力或力矩的传递率，如图2所示[6]。

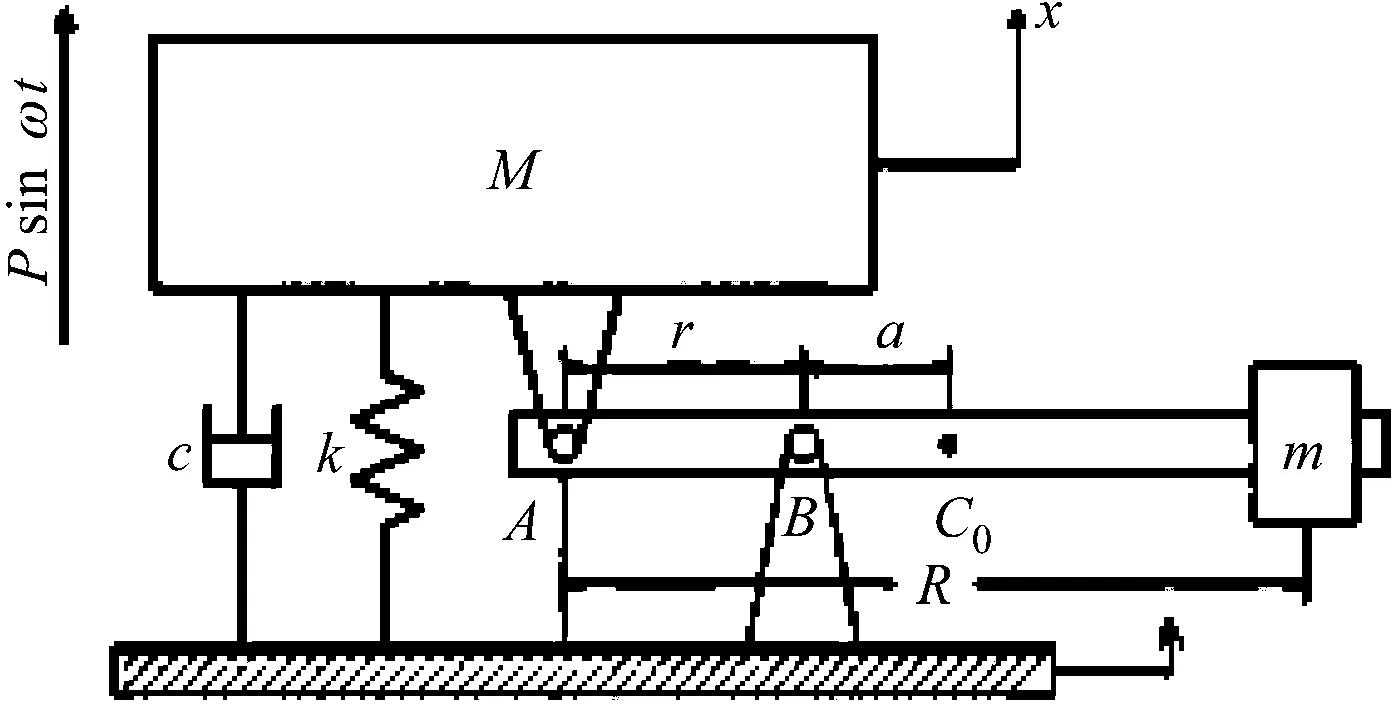
图1 动力反共振隔振器简化模型Fig.1 Anti-resonant vibration isolator

图2 聚焦式主减隔振系统简化模型Fig.2 Focal gearbox vibration isolation system

国外主减隔振技术发展至今已经非常完善和成熟，应用较为广泛的主减隔振系统为聚焦式主减隔振系统和聚焦反共振主减隔振系统。两种隔振系统区别在于聚焦反共振主减隔振系统在聚焦式主减隔振系统基础上增加了反共振隔振器设计，如图1和图2所示。聚焦反共振主减隔振系统在国外多型直升机应用并取得了较好的减振效果[8-13]，如虎式、茶隼等。相比国外国内主减隔振技术研究工作起步较晚，黄传跃、顾仲权、邓旭东、宋楚晨等人对直升机主减隔振装置进行研究并取得了一定的成果，但研究成果基本处于试验室阶段，由于技术成熟度的不足或缺乏装机可行性而没有进入型号应用。目前国产直升机大多仍使用聚焦式主减隔振系统。

本文以某型直升机为背景机，在原机聚焦式主减隔振系统基础上，设计了一种新型聚焦式反共振主减隔振装置，建立了三维参数化分析模型[14]，从隔振机理上对主减隔振装置的重要参数进行计算分析，并完成关键设计参数对主减隔振装置的隔振效率和动力学特性的影响进行分析评估。根据某型机的主减/机体安装接口完成新型聚焦式主减隔振装置的全尺寸工程样件设计与制造。经地面试验实测载荷传递以及振动水平验证，新型聚焦反共振式主减隔振装置在垂向、航向和侧向激励下减隔振效率达到了80%，为新研直升机以及现役直升机减隔振需求提供一条新的途径。

将动力反共振隔振器与聚焦式主减隔振系统结合起来，根据安装空间进行结构设计形成新型聚焦反共振式主减隔振系统，如图3所示。

图3 新型聚焦反共振式系统结构图与实物照片Fig.3 The structure of focal anti-resonant gearbox vibration isolation system

根据主减结构本身具有的对称性，将主减以及主减隔振装置进行适当简化，如图4所示。坐标xoz为整体坐标，O点为主减撑杆的虚焦点。对主减与机体做如下假设：假设主减有三个位移自由度z0，θ0，α0，直升机机体有五个位移自由度z1，θ1，α1，x1，y1。其中θ0与θ1分别为主减和机身以虚焦点为旋转中心绕X轴旋转的角度，α0与α1分别为主减和机身以虚焦点为旋转中心绕Y轴旋转的角度，z0，z1，x1，y1分别为主减和机体的沿着坐标系的平动位移。机身和主减的重量远大于撑杆的重量，为简化方程并突出系统的主要特性，忽略主减撑杆等杆件的质量和转动惯量。

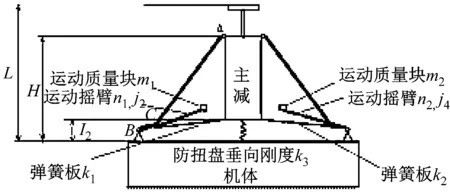
图4 聚焦反共振式系统简化模型Fig.4 Focal anti-resonant gearbox vibration isolation system

1.3 方程建立过程

1.3.1 由z0引起的运动方程

如图3所示A点坐标为：[-r1，-R1，H-L+z0]；B点坐标为：[-L11，-L2/2，-L+z1]；D点坐标为：[-r3，-R3，h-L+z0]；A′点坐标为：[r2，-R2,H′-L+z0]；B′点坐标为：[L12，-L2/2，-L+z1]；D′点坐标为：[r4，-R4,h′-L+z0]。

向量BA可以写为：[-r1+L11，-R1+L2/2，H+zz]，如图3所示在三角形ABC中，AC为l1，BC为l2根据三角形余弦定理，AB的长度由BA计算得出，则在三角形ABC中计算得到AB与BC之间的夹角记为β,BC与X轴的夹角记为β1。其中zz=z0-z1。

(1)

(2)

将向量BA单位化，得到单位向量n0

(3)

式中：

根据向量的旋转公式、BA向量的单位向量、BA和BC的夹角β以及BC与XOZ平面的夹角β1，根据向量旋转公式(旋转矩阵记为A)，得到BC方向的单位向量n1。

A=T1T2T3

(4)

根据BC方向的单位向量n1和B点坐标，以及BC长度l2，得到C点在运动时的坐标，即C点的位移。

C点的位移可简化表示为(cx1+Ox1z1+Px1z0，cy1+Oy1z1+Py1z0，cz1+Oz1z1+Pz1z0)。由于总体坐标系左边与右边C′点的位移不同，右边的C′点位移可以利用上述同样方法计算得到，简化表示为：(cx2+Ox2z1+Px2z0，cy2+Oy2z1+Py2z0，cz2+Oz2z1+Pz2z0)，得到C点坐标后根据几何关系可以计算出运动质量块处m1与m2处的位移。

1.3.2 由θ0引起的运动方程

由θ0引起的运动方程与由z0引起的运动方程推导方法类似

A点的坐标为：[(H-L)sinθ0-r1cosθ0，-R1，(H-L)cosθ0+r1sinθ0]；

B点的坐标为：[-L11cosθ1-Lsinθ1-L2/2，L11sinθ1-Lcosθ1]；

D点的坐标为：[(h-L)sinθ0-r3cosθ0-R3，(h-L)cosθ0+r3sinθ0]；

A′点坐标为：[(H′-L)sinθ0+r2cosθ0-R2，(H′-L)cosθ0-r2sinθ0]；

B′点坐标为：[-Lsinθ1+L12cosθ1-L2/2，-L12sinθ1-Lcosθ1]；

D′点坐标为：[(h′-L)sinθ0+r4cosθ0-R4，(h′-L)cosθ0-r4sinθ0]。

可以得到C点的位移坐标并简化为

(dx1+Qx1θ1+qx1θ0，dy1+Qy1θ1+qy1θ0，dz1+

Qz1θ1+qz1θ0)

右边C′点可以简化表示为

(dx2+Qx2θ1+qx2θ0，dy2+Qy2θ1+qy2θ0，dz2+

Qz2θ1+qz2θ0)

1.3.3 由α0引起的运动方程

由α0引起的运动方程与由z0引起的运动方程推导方法类似：

A点的坐标为：[-r1，-R1cosα0-(H-L)sinα0，(H-L)cosα0-R1sinα0]；

B点的坐标为：[-L11，-L2/2cosα1+Lsinα1，-Lcosα1-L2/2sinα1]；

D点的坐标为：[-r3，-R3cosα0-(h-L)sinα0，(h-L)cosα0-R3sinα0]；

A′点坐标为：[r2，-R2cosα0-(H′-L)sinα0，(H′-L)cosα0-R2sinα0]；

B′点坐标为：[L12，-L2/2cosα1+Lsinα1，-Lcosα1-L2/2sinα1]；

D′点坐标为：[-r4，-R4cosα0-(h′-L)sinα0，(h′-L)cosα0-R4sinα0]。

可以得到C点的位移坐标并简化为

(ex1+Tx1α1+tx1α0,ey1+Ty1α1+ty1α0,ez1+

Tz1α1+tz1α0)

右边C′点可以简化表示为

(ex2+Tx2α1+tx2α0,ey2+Ty2α1+ty2α0,ez2+

Tz2α1+tz2α0)

系统总运动方程

综合上两节，通过各连接点的位移，可以计算系统各部分的动能，通过能量叠加得到由主减z0、θ0和α0运动引起的总动能T。根据弹簧板以及防扭盘的刚度，得到系统运动过程中的总势能U。为简化方程突出关键参数的影响忽略阻尼的影响，根据拉格朗日方程，建立聚焦反共振式主减隔振系统在三维空间内运动引起的振动方程。

(5)

总动能为：T=T1+T2+T3+T4+T5

(6)

(7)

(8)

(9)

(10)

总势能可以表示为：U=U1+U2+U3+U4+U5

(11)

(12)

(13)

(14)

(15)

将式(6)～式(15)代入式(5)，整理后得到

系统总振动方程为

(16)

在正弦激励条件下，可知式(16)的稳态解呈正弦形式。载荷传递率如式(17)、式(18)和式(19)所示

(17)

(18)

(19)

2 参数影响分析及优化

主减/机体以及主减与机体平台的接口尺寸，主减与机体上点A与点B坐标参数、主减的高度参数以及连接各点的杆件长度包括主减撑杆长度、弹簧板长度与运动摇臂长度等结构参数，如表1所示。

外载荷激励频率25.5 Hz。

表1 结构参数Tab.1 Structure parameters

2.1 各参数对系统性能的影响分析

受安装空间接口尺寸限制，实际结构设计中隔振系统的空间尺寸不能改变，故而选取运动质量块质量以及弹簧板刚度m1,m2,K1,K2作为设计参数，由于垂向动载荷是引起机体振动的主要载荷，因此分析了设计参数对隔振系统垂向载荷隔振效果的影响。结果如图5～图8所示。

图5 运动块质量对隔振系统频率的影响

Fig.5 Influence of the moving mass on the natural frequency of the vibration isolation system

图6 运动块质量对隔振系统传递率的影响

Fig.6 Influence of the moving mass on Z-force transmissibility of the vibration isolation system

运动质量块质量和弹簧板刚度对隔振系统的固有频率以及主减隔振装置的反共振频率有比较大的影响，系统垂向固有频率和主减隔振装置反共振频率随着运动质量块质量的增加而减小，如图5和图7所示。系统垂向固有频率和主减隔振装置反共振频率随着弹簧板刚度的增加而增大。根据图6和图8所示的传递率曲线中，反共振频率随前后质量块质量以及前后弹簧板刚度的变化并不沿着对角线变化，说明前后质量块质量和前后弹簧板刚度对主减隔振反共振频率的影响程度是不同的。系统固有频率低于主减隔振装置反共振频率，两者相差不大，且同时与m1,m2,K1,K2四个参数有关。为了使三向传递率在激励频率下达到最小，对m1,m2,K1,K2这四个参数进行优化，转化为典型的多目标多参数的优化问题。在进行参数优化时，需将弹簧板刚度进行适当约束，弹簧板刚度对主减安装系统刚度有较大影响，弹簧板刚度太弱会直接导致主减系统在旋翼拉力载荷作用下产生较大的变形，对传动和操纵系统产生不利的影响。

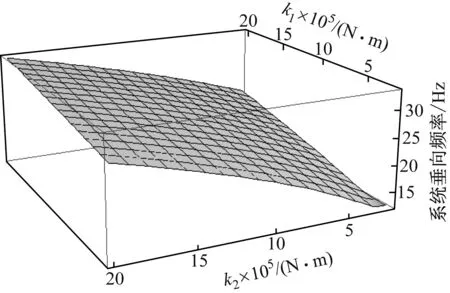
图7 弹簧板刚度对隔振系统频率的影响

Fig.7 Influence of the spring stiffness onthe natural frequency of the vibrationisolation system

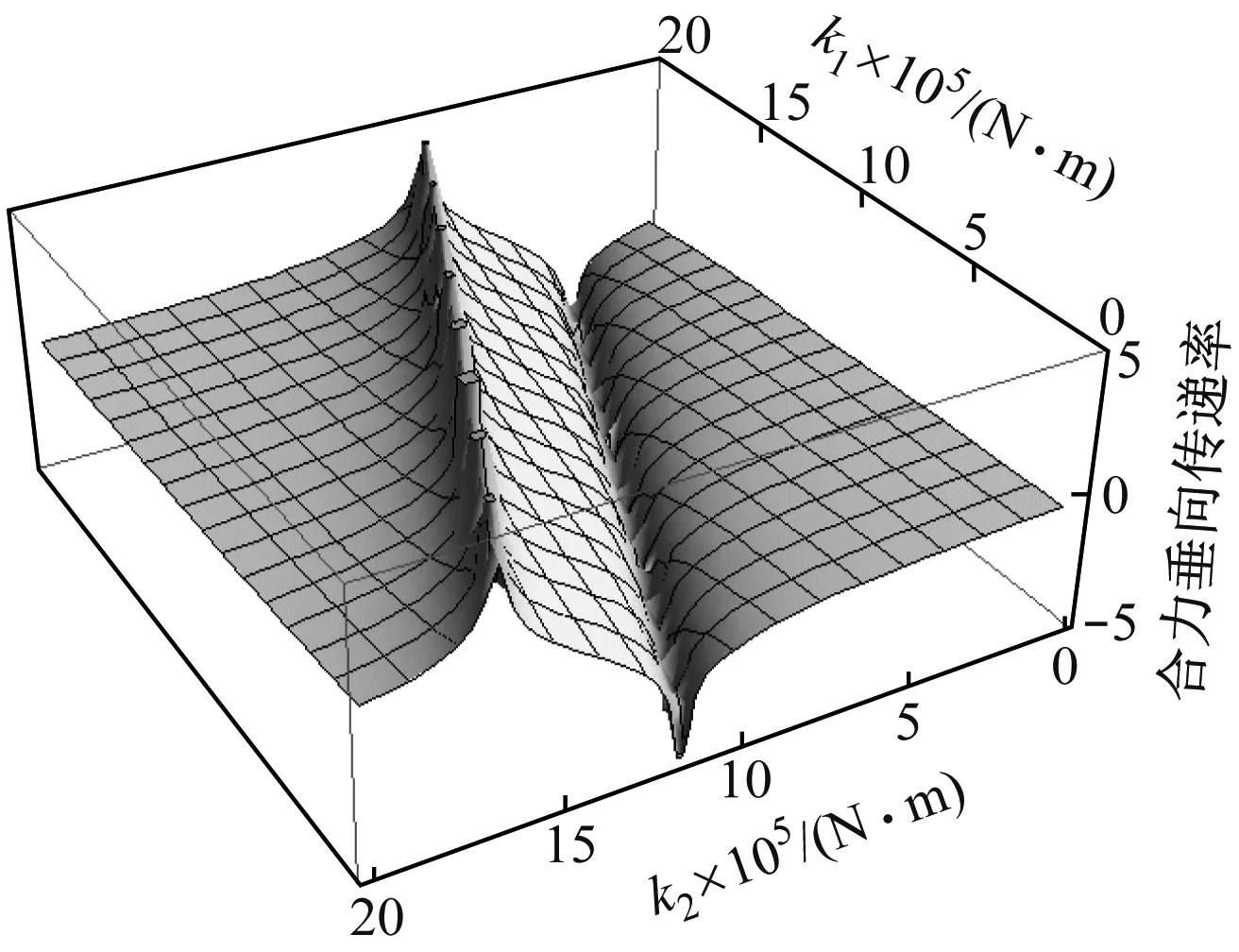
图8 弹簧板刚度对隔振系统传递率的影响

Fig.8 Influence of the spring stiffness on Z-force transmissibility of the vibration isolationsystem

2.2 参数优化

综合考虑在激励频率下三向传递率，对主减隔振装置设计参数进行优化，以f1(X)、f2(X)和f3(X)分别表示三向传递率的目标函数。通过统一目标函数法中的线性加权和法将三个子目标函数构造为一个新的目标函数f(X),新的目标函数成为统一目标函数，以新目标函数作为该多目标函数的评价函数，从而将多目标函数转化为单目标函数求解[15-17]。

(20)

式中：D为可行域。

由于设计变量值相差较大，先将各子函数进行无量纲归一化处理，再对各子目标函数进行线性加权处理，得到新目标函数

(21)

式中：各权系数ωi满足归一性和非负性条件，可根据各子目标函数的极小值应用α方法确定权重，得到ω1=0.34，ω2=0.33，ω3=0.33。

该优化问题设计参数为X=(m1,m2,K1,K2)，各分量上下限范围，如表2所示。

表2 设计参数限值Tab.2 Limit values of design variables

以主减安装刚度为约束条件，推导安装主减隔振装置后主减安装刚度表达式，得到主减安装刚度与弹簧板刚度之间的关系，在保证主减安装刚度与原机相当的约束条件下进行优化。根据式(16)所示，去除质量和加速度项后，转化为静力学问题

Kxi=fi

(22)

根据式(22)计算在主减载荷fi作用下主减和机体的位移xi，得到在垂向载荷作用下主减和机体的垂向位移分别z0和z1。主减垂向安装刚度表示为K′=fi/|z1-z0|，得到刚度约束表达式为

K′=fi/|z1-z0|≥K原机

(23)

2.3 参数优化结果

遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化搜索算法。通过MATLAB软件编制优化程序，采用遗传算法进行优化计算，得到目标评价函数随迭代次数变化的迭代图，如图9所示。由图9可知，目标评价函数随着迭代次数的增加有明显的降低，最终收敛为0.037。同时得到在目标评价函数达到最小值时m1,m2,K1,K2的值，为了便于结构设计将计算得到的m1,m2,K1,K2取整后作为实际结构设计值，如表3所示。将实际设计值代入式(17)、式(18)和式(19)即可求得传递率随频率Tz,Tha,Tce变化曲线，如图10～图12所示。

表3 设计参数优化结果Tab.3 Optimization values of design variables

图9 目标评价函数迭代图Fig.9 Variation of evaluation function values

图10 垂向力传递率频域计算曲线Fig.10 Z-force transmissibility calculated curve of vibration isolation system

图11 航向合弯矩传递率频域计算曲线Fig.11 X-moment transmissibilitycalculated curve of vibration isolation system

图12 侧向合弯矩传递率频域计算曲线Fig.12 Y-moment transmissibility calculated curve of vibration isolation system

3 试验结果验证

为了验证聚焦反共振式主减隔振系统性能，试验工作根据时间先后分为两个部分：地面台架试验与地面装机试验，地面台架试验采用力传感器实测垂向载荷、航向和侧向弯矩传递率，同时对比测试原机状态与隔振状态配重板(模拟机体)的振动水平。地面台架试验理论计算结果与实测主减安装频率及载荷传递率结果对比，结果如表4和表5所示。

表4模态频率计算与实测结果对比

Tab.4ComparisonoffrequenciesofexperimentandanalysisresultsHz

表5在25.5Hz处传递率计算与实测结果对比

Tab.5Comparisonof25.5Hztransmissibilityofexperimentandanalysisresults

模态实测载荷激励载荷实测传递率/%计算传递率/%垂向总合力41．5N306．2N13．64航向总弯矩28．3N·m559．6N·m4．73．6侧向总弯矩19．2N·m293．6N·m6．55．2

根据表4和表5结果，系统固有频率计算值与试验值比较接近，最大误差为6.3%。在25.5 Hz激励频率下传递率侧向和航向计算值与试验值比较接近，垂向合力传递率误差较大，其原因如下：根据图10～图12所示，在反共振点25.5 Hz频点处，垂向传递率较航向和侧向弯矩传递率隔振带宽较窄。垂向合力传递率隔振带宽与主减隔振装置阻尼有关，主减隔振装置为机械连接，阻尼较小。由于结构尺寸加工误差以及连接刚度等原因导致主减隔振装置与设计时有差异，反共振点发生移动，导致计算值与试验相差较大。由于隔振后载荷较小，测量误差也会导致计算值与实测值出现一定的偏差。

图13 实测垂向合力传递率幅频曲线

Fig.13 Z-force transmissibility practical frequency domain curve of vibration isolation system

图14 实测垂向传递合力时域曲线

Fig.14 X-moment transmissibility practical timedomain curve of vibration isolation system

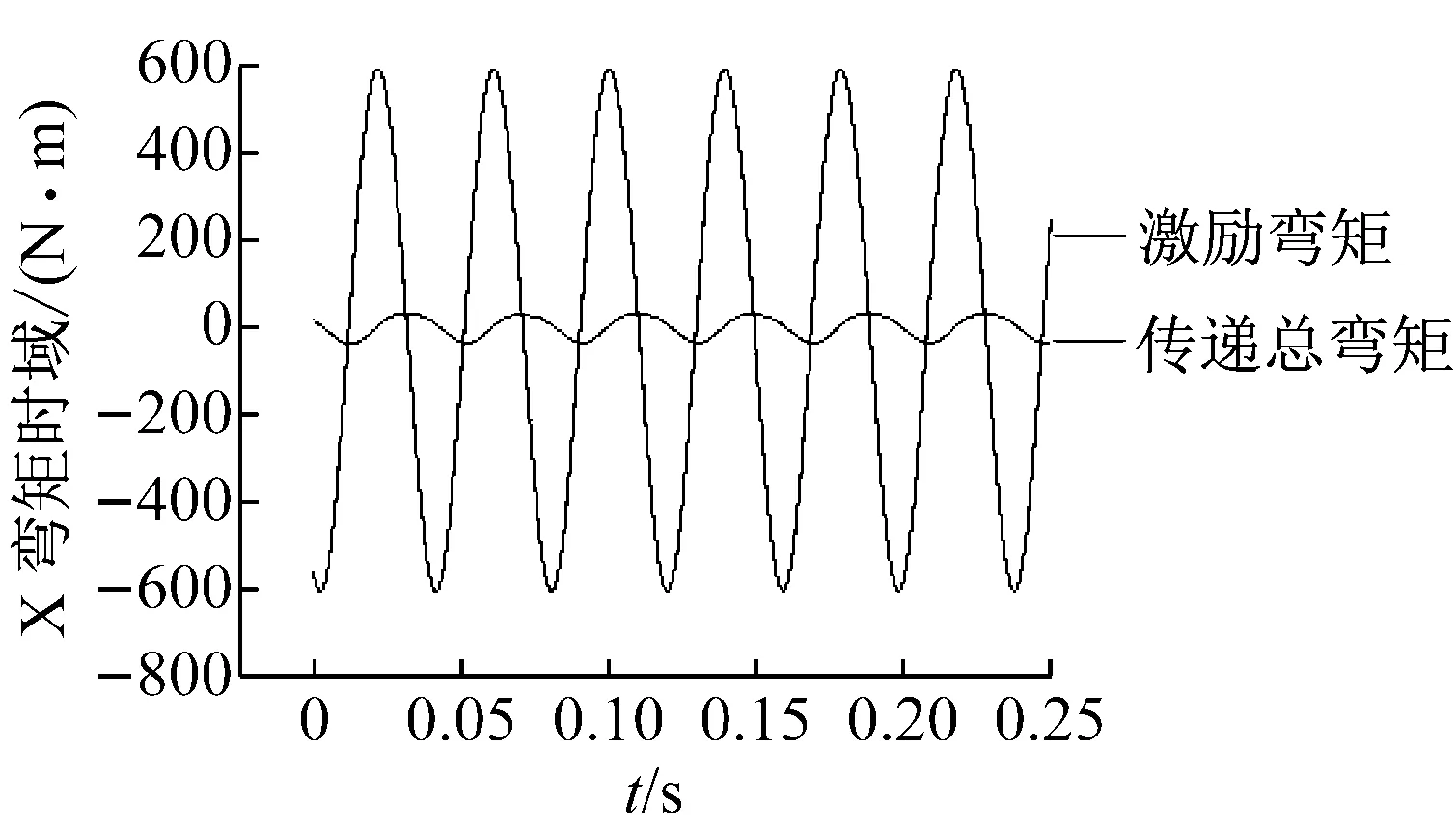
图15 实测航向传递合弯矩时域曲线

Fig.15 X-moment transmissibility practical timedomain curve of vibration isolation system

图16 实测侧向传递合弯矩时域曲线

Fig.16 Y-moment transmissibility practical time domain curve of vibration isolation system

图17 台架试验定频激励下隔振状态与原机状态实测振动水平对比

Fig.17 Comparison of the vibration level under vertical excitation in the ground bench test

完成地面台架试验后进一步考核聚焦反共振式主减隔振系统的性能，为后续型号应用奠定基础，装上某型机真机后进行地面全机振动水平对比测试，选取关键位置处振动水平进行对比。

表6 台架试验定频激励下隔振状态与原机状态实测振动水平对比Tab.6 Comparison of the vibration level under vertical excitation in the ground bench test unit g

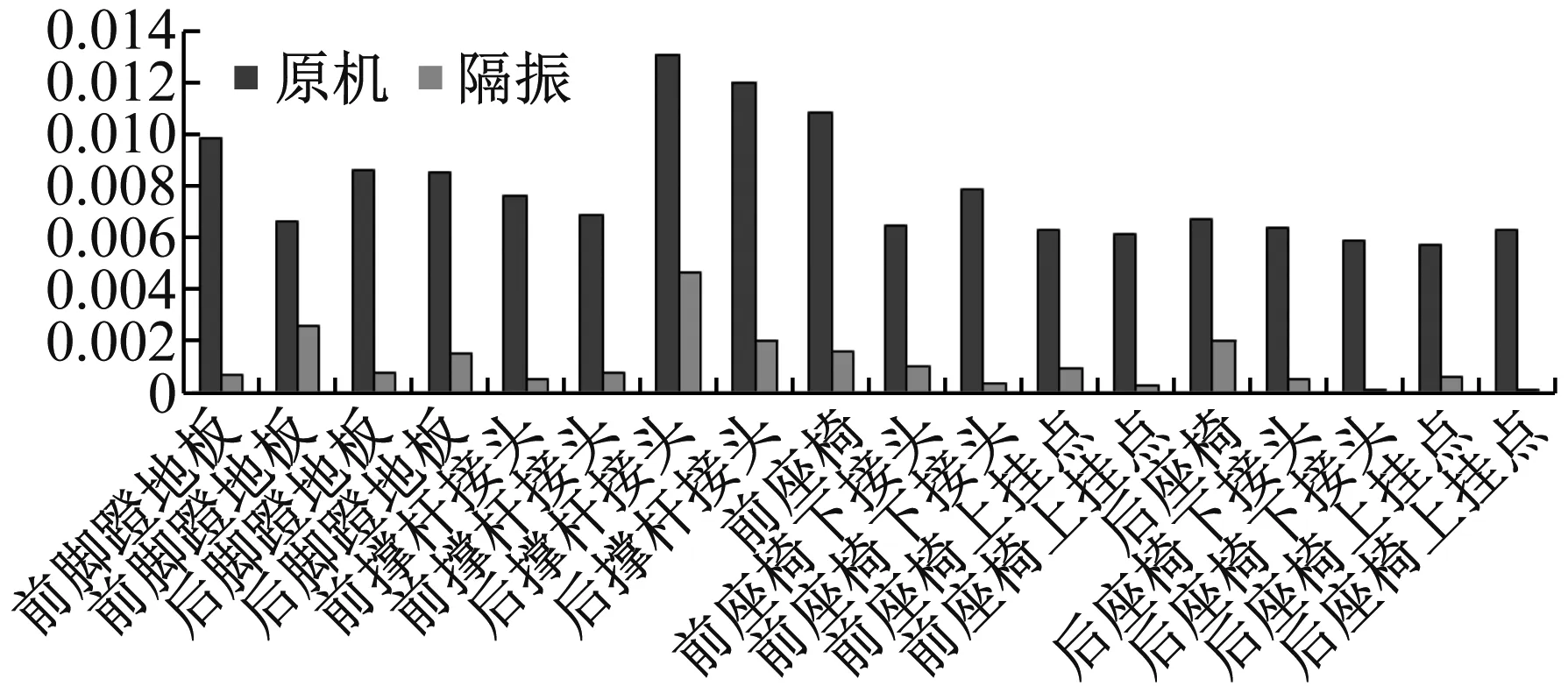
图18 装机状态下垂向定频激励时隔振状态与原机状态实测振动水平对比

Fig.18 Comparison of the vibration level under vertical excitation in the ground assembling test

图19 装机状态下航向定频激励时隔振状态与原机状态实测振动水平对比

Fig.19 Comparison of the vibration level under longitudinal excitation in the ground assembling test

4 结 论

本文从型号实际需求出发，以某型机为背景机，提出一种新型聚焦反共振式主减隔振装置，通过建模计算以及试验验证，得出如下结论：

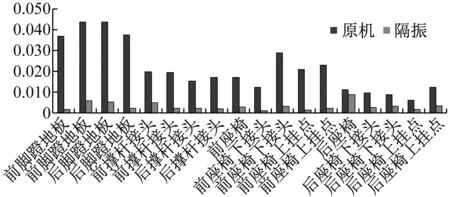
图20 装机状态下侧向定频激励时隔振状态与原机状态实测振动水平对比

Fig.20 Comparison of the vibration level under lateral excitation in the ground assembling test

(1) 将反共振隔振器与聚焦式主减隔振系统结合，形成聚焦反共振式隔振系统。聚焦反共振式隔振系统不仅可以隔离旋翼平面内的载荷，还可以隔离旋翼垂向载荷，同时保证主减垂向安装刚度要求。

(2) 聚焦反共振式主减隔振系统运动质量块以及弹簧板刚度m1,m2,K1,K2对系统频率以及隔振传递率有较大的影响，增大质量会降低系统的固有频率，增大弹簧板刚度会提高系统的固有频率，从隔振角度看固有频率降低对隔振是有利的，但质量和刚度的改变会带来反共振点的改变，引起隔振系统隔振性能的改变，同时减小刚度会引起主减的位移过大，所以在进行结构设计时应该综合考虑各参数的影响。

(3) 本文建立了聚焦反共振式主减隔振系统三维参数化计算分析模型，经验证其计算结果与试验结果有较好的一致性，并使用该模型分析了设计参数对隔振系统频率和传递率的影响；参数化模型可作为后续的结构优化设计分析模型，同时该模型可以克服因设计初期结构未确定而无法使用有限元计算的困难，有利于缩短设计周期。

(4) 本项目以某型直升机实际结构为设计边界，提出了一种新型聚焦反共振式主减隔振装置，通过计算、地面台架以及地面装机试验验证，充分说明新型聚集反共振式主减隔振系统有效地降低了机体的振动水平，三向减振效率>80%。聚焦反共振式主减隔振系统是一种有效的直升机减手段，通过本项目的研究工作实现了技术积累，为后续型号应用提供了一套有效可行的技术手段。

参 考 文 献

[1] 张晓谷.直升机动力学设计[M].北京：航空工业出版社，1995.

[2] 航空航天工业部科学技术研究院.直升机动力学手册[M].北京：航空工业出版社，1991.

[3] 顾仲权. 动力反共振隔振[J]. 噪声与振动控制,1989,21(6)：36-40.

GU Zhongquan. Dynamic anti-resonant vibration isolation[J]. Noise and Vibration Control,1989,21(6)：36-40.

[4] 宋楚晨. 直升机主旋翼半主动DAVI隔振系统设计[D]. 南京:南京航空航天大学,2014.

[5] 邓旭东. 直升机高性能主减隔振系统分析与仿真研究[D].南京:南京航空航天大学,2011.

[6] 王荇卫,程伟，诸德超，等.桅杆式瞄准具对直升机聚焦式隔振系统动态特性的影响研究[J]. 中国航空学报(英文版)，2003,16(4):217-222.

WANG Xingwei, CHENG Wei, ZHU Dechao, et al. Theoretical experimental and studies on the influence of the mast mounted sight (MMR) on the dynamic behavior of the focal isolation system(FIS) of helicopter[J]. Chinese Journal of Aeronautics,2003,16(4):217-222.

[7] 黄传跃,郭光海,李祖钊.一种新型旋翼/机身隔振装置及其性能分析[J]. 振动工程学报, 1999，12(3)：403-409.

HUANG Chuanyue, GUO Guanghai, LI Zuzhao. A new rotor fuselage vibration isolator and its characteristics analysis[J]. Journal of Vibration Engineering,1999，12(3)：403-409.

[8] KONSTANZER P. Recent advances in Eurocopter’s passive and active vibration control[C]//American Helicopter Society 64th Annual Forum. Montreal, 2008.

[9] HENDERSON J P. Vibration isolation for rotorcraft using electrical actuation[D]. Bath: University of Bath, 2012.

[10] KRYSINSKI T, MALBURET F. Mechanical vibrations: active and passive control[M]. New York: John Wiley & Sons,2010.

[11] KUMAR D. Design and analysis of composite rotor blades for active/passive vibration reduction[M]. Detroit, MI: The University of Michigan,2013.

[12] GUAN Y H, LIM T C, STEVE SHEPARD W. Experimental study on active vibration control of a gearbox system[J]. Journal of Sound and Vibration, 2005，282(3): 713-733.

[13] ASIRI S, BAZ A, PINES D. Periodic struts for gearbox support system[J]. Journal of Vibration and Control, 2005，11(6)：709-721.

[14] 沈安澜，陈静，刘续兴，等.直升机主减动特性三维参数化分析方法[J]. 直升机技术，2016(3)：18-25.

SHEN Anlan, CHEN Jing, LIU Xuxing, et al. A new three-dimensional mathematics analysis method of helicopter main gearbox dynamic characteristics[J]. Helicopter Technique,2016(3)：18-25.

[15] 杜恒，魏建华.基于遗传算法的连通式油气悬架平顺性与道路友好性参数优化[J].振动与冲击，2011，30(8)：133-138.

DU Heng,WEI Jianhua.Parameters optimization of interconnected hydro-pneumatic suspension for road comfort and road-friendliness based on genetic algorithm[J].Journal of Vibration and Shock，2011，30(8)：133-138.

[16] 吕彭民，和丽梅，尤晋闵.基于舒适性和轮胎动载的车辆悬架参数优化[J].中国公路学报，2007(1)：112-117.

LÜ Pengmin,HE Limei,YOU Jinmin. Optimization of vehicle suspension parameters based on comfort and tyre dynamic load[J]. China Journal of Highway and Transport,2007(1)：112-117.

[17] 杨荣山，黄向东，袁仲荣，等.多目标优化方法在悬架几何设计上的应用[J].华南理工大学学报(自然科学版)，2009(7)：85-89.

YANG Rongshan,HUANG Xiangdong,YUAN Zhongrong, et al. Application of multi-objective optimization methods to geometric design of suspension[J].Journal of South China University of Technology(Natural Science Edition),2009(7)：85-89.