弹性圆环在刚壁上的撞击回弹

李凤云， 吴志鹏， 郑宇轩， 周风华， 余同希,2(. 宁波大学 冲击与安全工程教育部重点实验室，宁波 352； 2. 香港科技大学 机械工程系，中国 香港 999077)

日常生活和工程实践中充斥着大量的碰撞事件。高速行驶汽车间的碰撞，汽车撞击护栏、树木等固定物，船舶间的碰撞及撞击桥墩等，诸如此类的碰撞事件给社会经济和人身安全都造成了巨大的危害。圆柱壳或圆环结构作为常用的缓冲吸能结构，其在撞击过程中的力学响应、结构的变形模式、能量的交换和吸收以及撞击后的回弹行为备受关注[1-8]。

早期对于圆环的研究中，主要方向在于塑性环状结构的大变形，分别从准静态和动载作用两方面进行了分析。Deruntz等[9]在分析准静态压缩下薄壁圆管结构时，最先提出了四铰机理。Yu[10]则从结构的角度上，对刚塑性圆环在一对径向拉力作用下进行了分析。Reid等[11-12]对于准静态和动态加载下的塑性圆环进行了系统性的研究，得到了大量的实验数据和理论分析，为工程设计提供可靠的依据。

作者前期研究工作表明弹塑性圆环撞击刚壁后，在较低初始速度下(0.2倍的圆环屈服速度内，通常小于10 m/s)，此时弹塑性圆环只有弹性变形，回弹速度与初始撞击速度成正比，恢复系数COR为定值，且其数值在3/4左右，表明仅有9/16的圆环初始动能转化为回弹后的平动动能，另外7/16的圆环初始动能以弹性波传播和弹性变形的形式存在。本文进一步研究了一个完全弹性的圆环在广泛的初始速度范围内撞击刚性壁后的动力学响应，利用Abaqus/Explicit动力学程序模拟理想弹性圆环撞击刚性壁后的运动过程。同时，在理论上将圆环等效成曲梁，对其撞击刚性壁后的动态响应进行分析。并且研究了完全弹性圆环的初始撞击速度、直径、横截面积、弹性模量等参数对弹性圆环撞击刚性壁过程中恢复系数COR的影响。

1 弹性圆环撞击刚壁的数值模拟

建立如图1所示的有限元模型，圆环外径D=200 mm，内径d=180 mm，横截面为a×b=10 mm×10 mm的正方形，圆环弹性模量E=210 GPa，密度ρ=7 800 kg/m3，泊松比μ=0.29。圆环以一定速度垂直撞击刚性壁，整个撞击及回弹过程均为弹性变形。

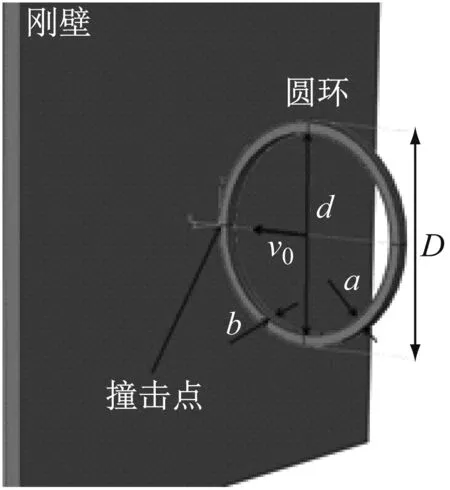
图1 有限元模型Fig.1 Finite element model

精确模拟圆环撞击刚壁及回弹过程需要网格尽可能精细，但过于精细的网格划分又需要过高的计算成本。为减少计算结果的网格依赖性，用不同尺寸的四面体(线性或二次)实体单元划分圆环。将圆环沿环向四等分切割，采用自由网格划分方式。通过指定4种不同的平均单元尺寸(在1/4圆环上布局数量分别为10，15，30，45的种子)，得到了8种不同单元密度及类型的有限元网格。采用Abaqus/Explicit动力学程序模拟初始速度为100 m/s的圆环垂直撞击刚性壁的过程，得到圆环的恢复系数值如图2所示，其中恢复系数COR为撞击回弹后的质心平动速度vr与撞击前的初始速度v0之比，即COR=vr/v0。可见，二次单元相对线性单元数值实验结果更加稳定。在下文的计算中，统一选取四面体二次网格进行计算，且1/4圆环上种子数量为30。

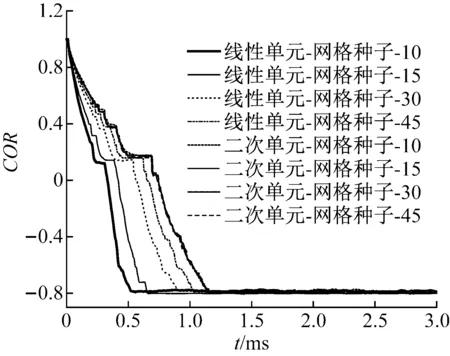
图2 不同网格密度及类型计算得到的恢复系数Fig.2 COR calculated using different meshes

图3给出了不同初始速度(0.01～600 m/s)的圆环垂直撞击刚性壁后的恢复系数，撞击速度小于200 m/s时，COR取值集中在0.75～0.8；当撞击速度达到400 m/s时，COR显著低于上述范围，其值在0.54以上。由此可见，日常的撞击情形(v0≤200 m/s)下，恢复系数与初始速度弱相关；而在更高撞击速度(v0≥400 m/s)时，恢复系数的变化有待进一步的研究。

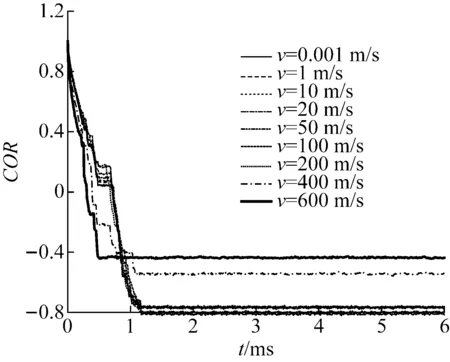
图3 圆环在不同初始速度下的恢复系数Fig.3 COR under different initial velocities

2 圆环撞击回弹理论分析

2.1 圆环自由振动方程[13-15]

圆环模型如如图4(a)所示，忽略转动惯量和剪切变形的影响，考虑如图4(b)所示的弹性圆环微元段abcd，其中u为径向位移，w为周向位移，P为曲梁轴力，F为曲梁剪力，M1为弯矩，f和p分别为沿径向和切向的外载荷，A为弹性圆环横截面的面积，R为圆环中性面的半径，ρ为圆环密度，得到在圆环面内的三个平衡微分方程。

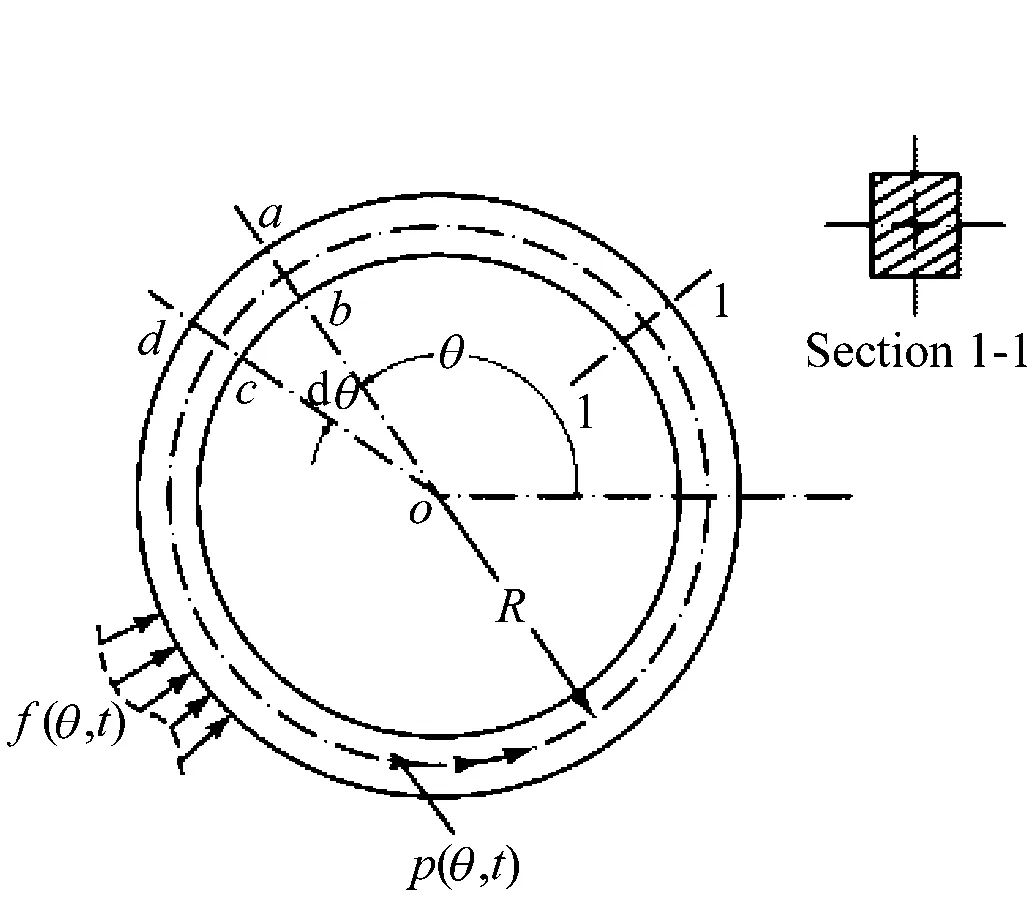
图4 弹性圆环微元Fig.4 Differential element of elastic-ring

(1)

几何方程

(2)

物理方程

σ=Eε

(3)

式中：ε为弹性圆环的径向应变；E为弹性模量；σ为圆环径向应力。

结合横断面力分析和周向中层不可压缩方程

(4)

并将平衡方程、几何方程以及物理方程都简化到关于周向位移w的方程，得到弹性圆环微元段的控制方程

(5)

式中：I1=∬AxdA，表示微元段横截面的转动惯量，式(5)即为圆环面内自由振动方程。

2.2 模态分析

对于圆环撞击后的自由振动过程，无外力f和p作用，即f=0以及p=0，振动方程简化为

(6)

假定圆环撞击后为谐波振动，则式(6)解的形式为

w(θ,t)=W(θ)eiωt

(7)

其中ω为圆环振动的频率。将式(7)代入式(6)可得

(8)

求解式(8)得

W(θ)=Csin(nθ+φ)

(9)

其中C和φ为常数。代入式(8)可得到圆环回弹后的振动频率

(10)

当n=1时，一阶振动频率ω1=0，表明圆环形状无变形，运动过程为刚体碰撞，故弹性圆环振动频率表达式从n=2开始。

2.3 圆环回弹后运动的频谱分析

圆环撞击刚性壁后，运动状态较为复杂，为平动加多模态振动形式，通过分析圆环回弹后径向和切向的速度规律，描绘圆环回弹后的运动形式。撞击之前，圆环无变形，以平动速度v0运动。垂直撞击刚性壁之后，各个位移分量的空间相位角为(轴对称碰撞)，圆环具有如下的周向和径向位移

(11)

其中，C1=vrt为圆环回弹后的质心水平位移，Cn为各阶模态系数，M为振形阶数，φn为时间相位。

将式(11)对位移进行一阶求导可得圆环的周向速度和径向速度

(12)

从式(12)可以看出，n=1时，圆环只有平动；n>1时，既有平动，又有更高阶的运动形式。由于圆环上任意截面的速度都能反应其频谱特点，故选取圆环撞击截面的径向速度进行频谱分析，考虑到COR与撞击速度的弱相关性，选取初始速度为v0=1 m/s、v0=10 m/s、v0=100 m/s和v0=200 m/s的四种圆环进行频谱分析。截取频率以内的点，去除回弹后平动速度vr(即圆环的平动)，频谱分析如图5所示。

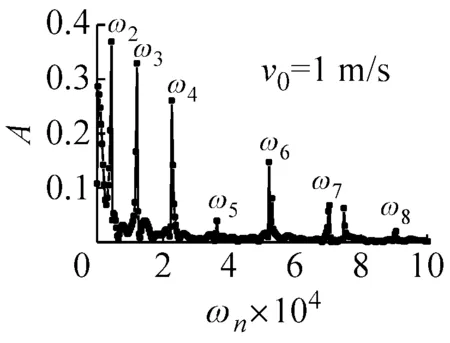
(a) 初始速度为1 m/s的圆环频谱分析

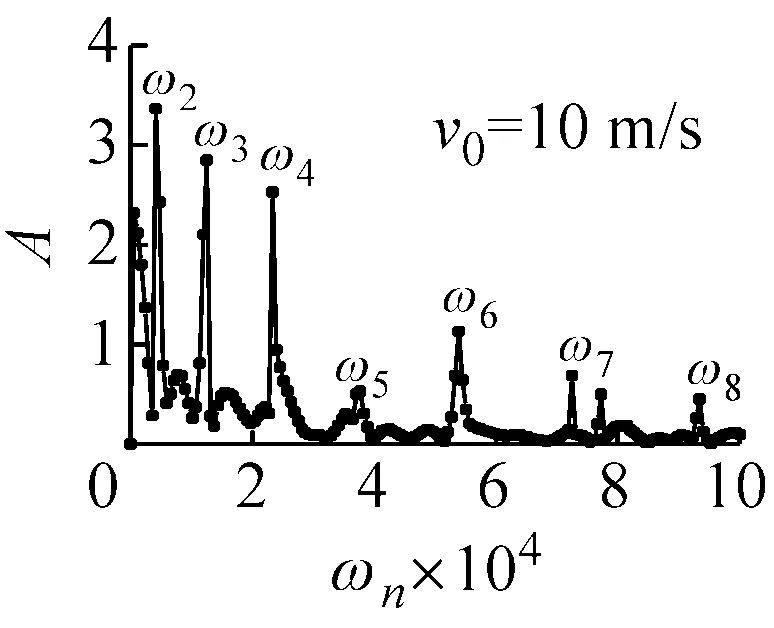
(b) 初始速度为10 m/s的圆环频谱分析

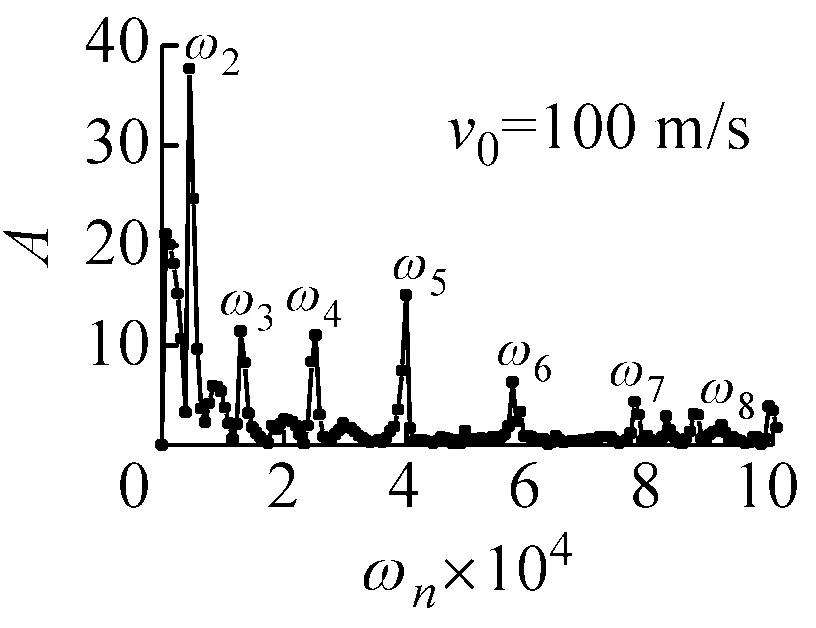
(c) 初始速度为100 m/s的圆环频谱分析

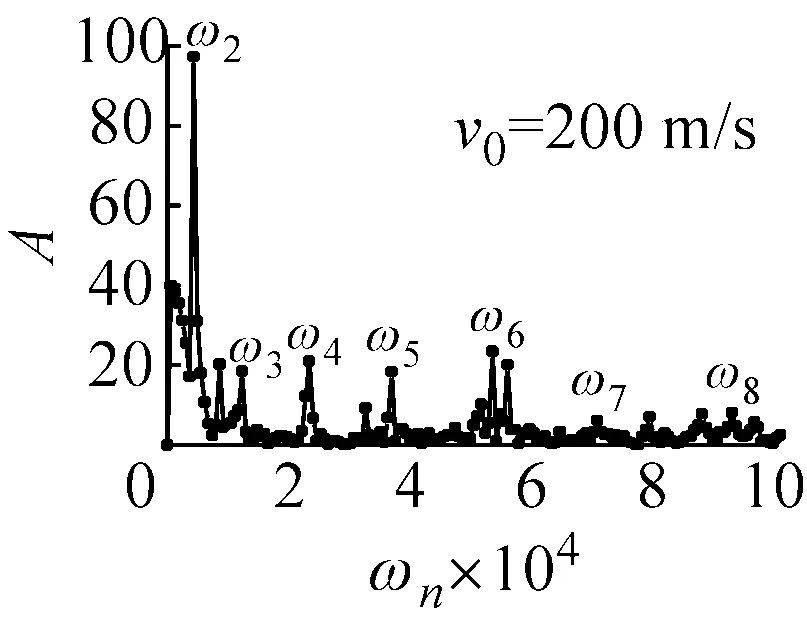
(d) 初始速度为200 m/s的圆环频谱分析图5 弹性圆环回弹后频谱分析图Fig.5 Spectral analysis of the elastic ring

根据式(10)，得出数值计算中弹性圆环回弹后各阶的振动频率，并结合上述数值模拟后的结果(选取v0=1 m/s)，得到表1所示的圆环回弹后振动过程中ω2～ω8的振动频率对比情况。

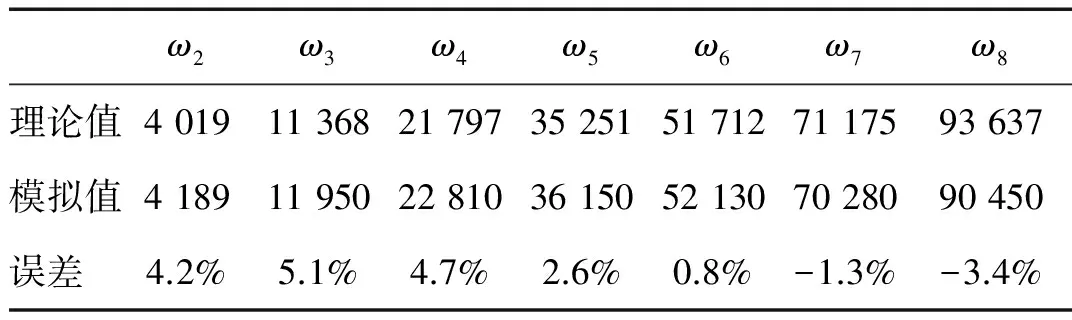
表1 各阶振型振动频率ωnTab.1 The frequency ωn in the various modes of vibration

图5中纵坐标表示各频率对应的幅值An，由An=nωnCn推出各频率对应的Cn的值，从而得到各阶模态的系数分布。以v0=1 m/s的情况为例，对比C1和各阶模态系数(如图6所示)可以看出，2阶及后续模态呈递减趋势，且2阶之后的频率占比非常小，其总和远小于前两阶所占比。所以圆环回弹后的运动是以1阶和2阶振动模态为主的自由振动，故振动的模态主要集中在低阶状态，与数值模拟现象一致。

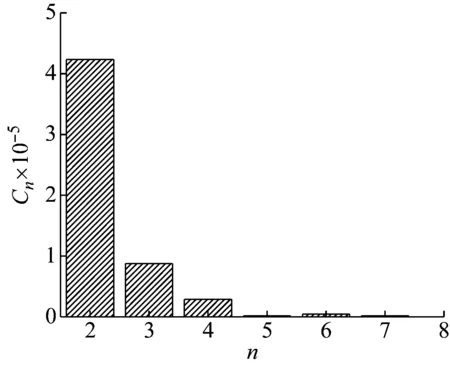
图6 初始速度为1 m/s的圆环Cn分布Fig.6 The distribution of Cn at the rate of 1 m/s

2.4 弹性圆环恢复系数的解析解

圆环撞击回弹后动能为

(13)

圆环各点的弯曲曲率表示为径向位移的微分形式，有

(14)

则势能

n2)]2sin2(ωnt+φn)

(15)

将式(10)代入式(15)，得到圆环动能T、势能U和总能量E的表达式分别为

(16)

(17)

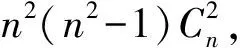
由能量守恒有

(18)

脱离时的几何条件：在圆环脱离刚性壁面瞬时(t=0)，圆环接触点(θ=0)的瞬时速度为0，则有

(19)

对于脱离时的物理条件，假定在圆环脱离壁面瞬时(t=0)系统势能最小，则有

sinφn=0⟹φn=0

(20)

代入式(19)，得

(21)

联立求解方程

(22)

式(22)为无限自由度系统，2个方程无法求解，只能做预估。M为最高振型，取M=2，即只存在平动和2阶振型，则有

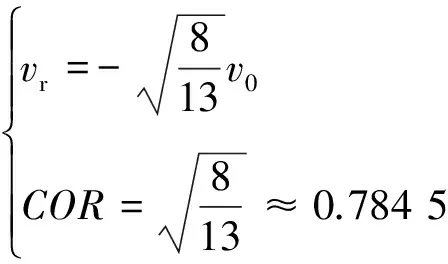
(23)

而对于高阶振形，M≥3，式(22)无法给出确定解(高阶振幅与撞击过程相联系)。假定存在n阶孤立振形，则有

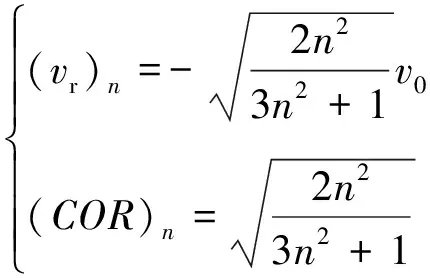
(24)

(25)

3 圆环几何及材料参数对COR的影响

3.1 圆环几何参数对COR的影响

同一模型，给定圆环速度v0=100 m/s，分别改变圆环的截面尺寸(a×b)和圆环外直径(D)，其它参数保持不变，COR对比如图7所示。

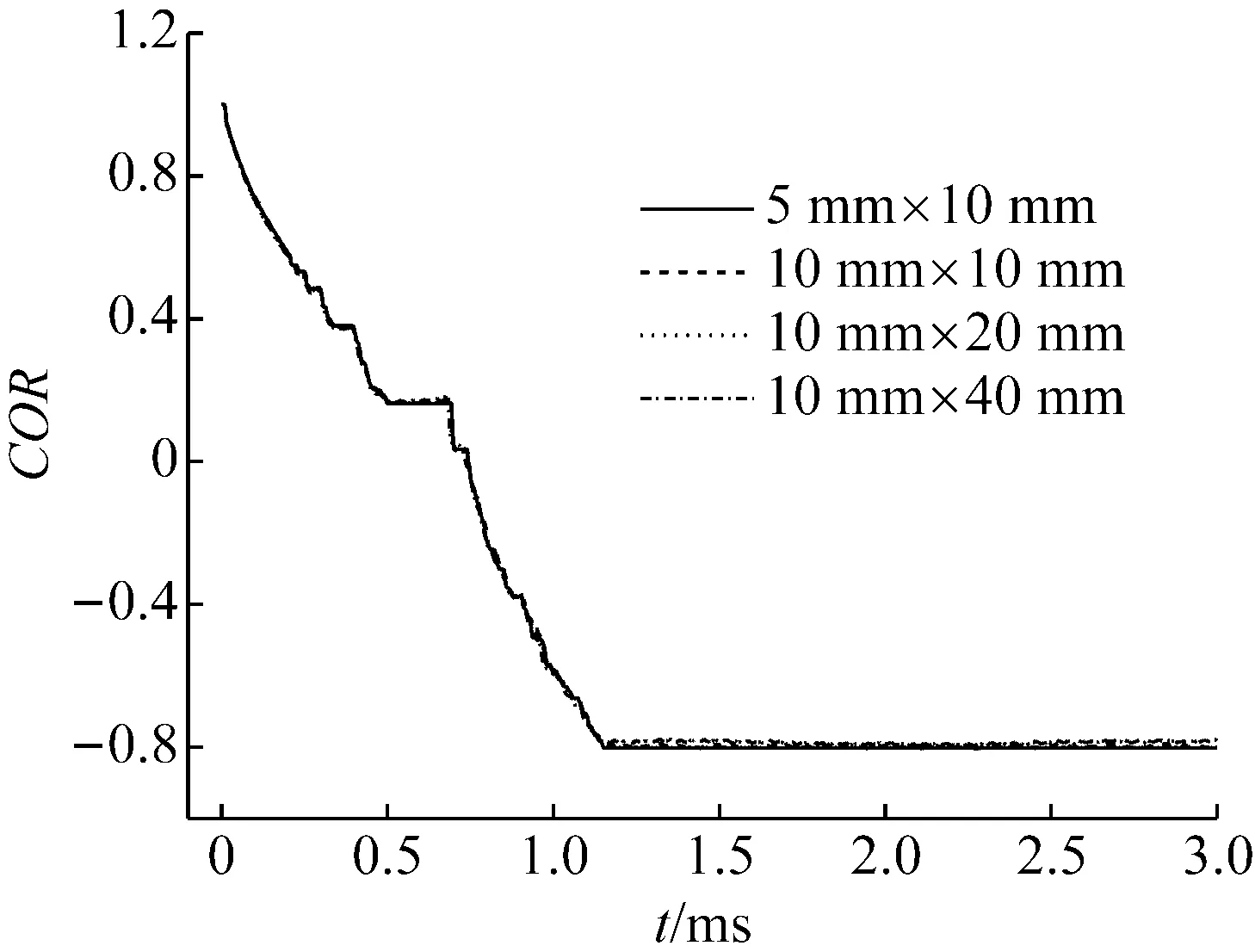
(a) 不同截面圆环的COR对比

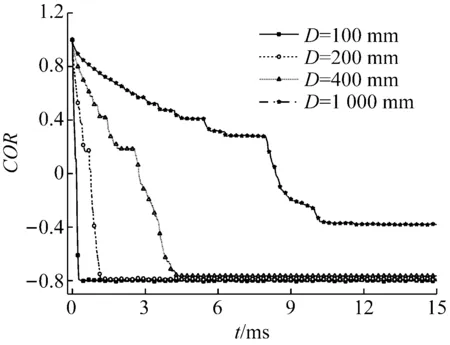
(b) 不同直径圆环的COR对比图7 不同尺寸圆环的COR对比Fig.7 The contrast of COR in different measurement

由图7(a)看出，其它参数不变，只改变截面尺寸，当a∶b在一定范围内(a∶b<1∶4)，不同截面尺寸的圆环COR变化趋势基本重合，且COR值在0.8附近，故COR与圆环截面尺寸呈弱相关关系。由图7(b)看出，其它参数不变，只改变直径大小，在一定的直径范围内(D<400 mm)，不同直径尺寸的圆环COR值稳定在0.8附近；但直径尺寸增加到一定范围时(如D=1 000 mm)，其COR值会明显降低。所以圆环COR值与圆环截面尺寸、圆环直径尺寸在一定范围内弱相关。

3.2 圆环弹性模量对COR的影响

保持模型其它参数不变，只改变材料弹性模量E(将圆环材料的E扩大或减小特定倍数)，COR对比如图8所示。

由图8可知，在一定条件下(E≥21 GPa)，弹性模量的改变对圆环COR无影响，其值同样落在0.75～0.8，可以近似看做与材料的弹性模量弱相关。但E减小到一定量(如E=2.1 GPa)，COR取值有显著的改变，曲线最后在0.2附近震荡，与前者有明显的差别。

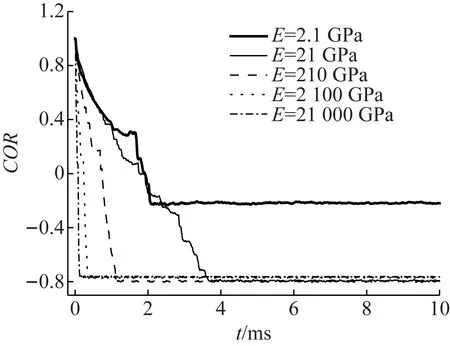
图8 不同弹性模量下的COR对比Fig.8 The contrast of COR in different elastic modulus

3.3 结果讨论

通过对上述情况的分析看出，在较广泛的参数范围内，如速度、截面、直径和弹性模量等的变化，对圆环COR值的影响很小，可以近似看作是弱相关。但在某些极端条件下，如高速、直径大幅增加或弹性模量的大幅减小等都会使COR的值显著下降。为此对撞击速度v0=400 m/s、圆环直径D=1 000 mm、弹性模量E=2.1 GPa三种情况下的圆环径向速度作频谱分析，如图9所示。

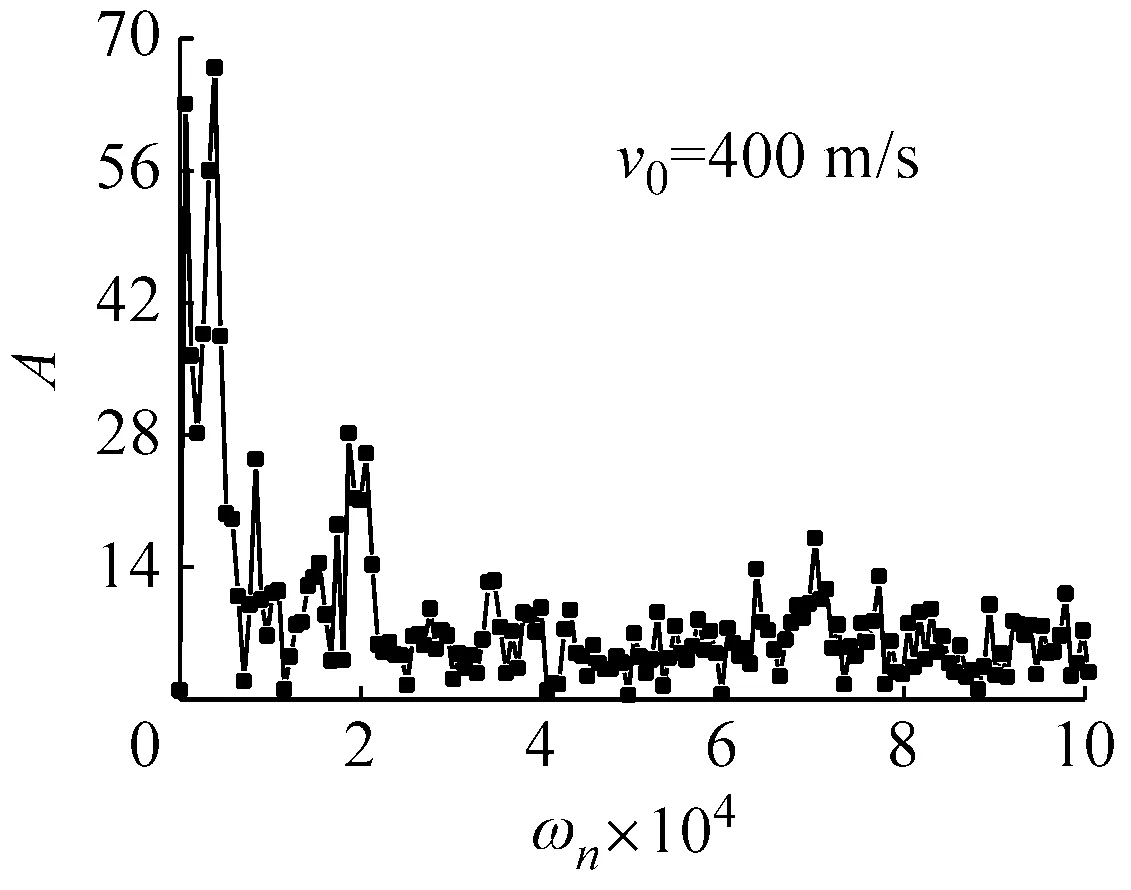
(a) 初始速度为400 m/s的圆环频谱分析

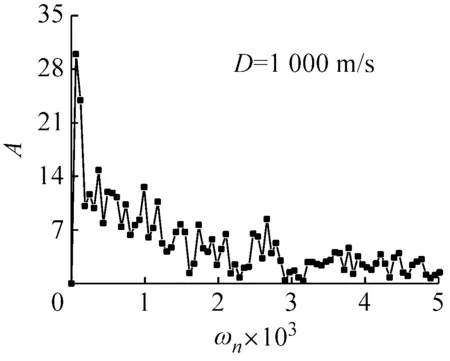
(b) 直径为1 000 mm的圆环频谱分析

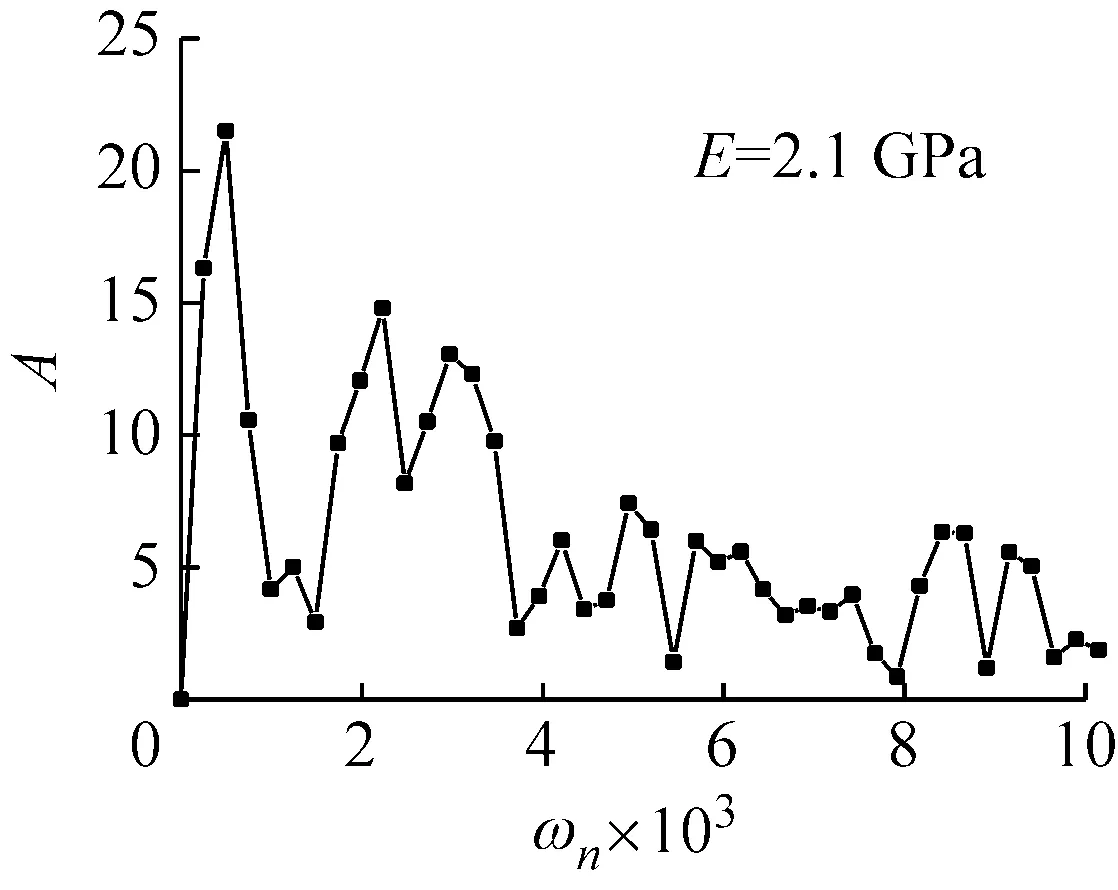
(c) 弹性模量为2.1 GPa的圆环频谱分析图9 三种情况下的圆环频谱分析Fig.9 Spectral analysis of three different situations

从图9中可以看出，在上述极端情况下，圆环径向速度的频谱分析中，振动频率显得杂乱无章，与图5所示的频谱分析结果有着显著差别，说明圆环回弹后振动形式异常复杂，从而造成COR值的显著改变。

4 结 论

数值计算了弹性圆环在不同初始速度下垂直撞击刚性壁回弹的过程，发现在一般情况下，恢复系数COR的值主要集中在0.76～0.8的狭窄范围内。

将弹性圆环等效成曲梁进行理论分析，得到圆环回弹后面内振动的各阶振型及相应频率的解析解。结合数值模拟的结果发现，在一般情况下，圆环在撞击刚性壁后的回弹是以一阶平动和二阶振动为主的运动形式。

在较广泛的参数范围内，如速度、截面、直径和弹性模量等的变化，对COR的影响很小，可以近似看作是弱相关。但在某些极端条件下，圆环的振动过程异常复杂，恢复系数发生了显著改变。

考虑到实际振动是由所有模态按一定的权重进行叠加组合，虽然低阶模态的所占比重比高阶模态高得多，但是也绝不仅仅是一阶模态能够完全描述的。从另一方面来讲，弹性圆环不同的入射速度所激发出来的振动模态比重必然也是不同的，所以恢复系数也存在着差异。再者，实际弹性圆环撞击中，弹性圆环与刚性壁分离的过程非常复杂，有限元模拟结果显示某些碰撞过程中，圆环和刚性壁完全分离之前会发生多次的分离和接触，且接触点随速度的不同也会有所变化。因此，后续工作将进一步分析多次碰撞是否会影响圆环的振动模态及恢复系数。

参 考 文 献

[1] ZHOU F H, YU T X, YANG L M. Elastic behavior of ring-on-foundation[J]. International Journal of Mechanical Sciences, 2012, 54(1):38-47.

[2] BAO R H, YU T X. Impact and rebound of an elastic-plastic ring on a rigid target[J]. International Journal of Mechanical Sciences, 2014, 91:55-63.

[3] XU S, DONG R, LU G, et al. Collision and rebounding of circular rings on rigid target[J]. International Journal of Impact Engineering, 2015, 79(3):14-21.

[4] 张铁光, 郭晓刚. 受横向冲击圆环的粘塑性大变形分析[J]. 爆炸与冲击, 1990(1):57-64.

ZHANG Tieguang, GUO Xiaogang. The large viscoplastic deformation of a ring subjected to lateral impulsive loading[J]. Explosion and Shock Waves, 1990(1):57-64.

[5] 余同希. 利用金属塑性变形原理的碰撞能量吸收装置[J]. 力学进展, 1986, 16(1):28-39

YU Tongxi. Impact energy absorbing devices based upon the plastic deformation of metallic elements[J]. Advances in Mechanics, 1986, 16(1):28-39.

[6] 赵凯, 沈建虎, 刘凯欣,等. 圆环列系统吸能特性研究[J]. 北京大学学报自然科学版, 2007, 43(3):312-316.

ZHAO Kai, SHEN Jianhu, LIU Kaixin,et al. Research on energy absorption feature of ring systems[J].Acta Scientiarum Naturalium Universitatis Pekinensis, 2007, 43(3): 312-316.

[7] ALGHAMDI A A A. Collapsible impact energy absorbers: an overview[J]. Thin-Walled Structures, 2001, 39(2):189-213.

[8] 余同希，邱信明. 冲击动力学[M]. 北京：清华大学出版社, 2011.

[9] DERUNTZ J A, HODGE P G. Crushing of a tube between rigid plates[J]. Journal of Applied Mechanics, 1962, 30(3):391-395.

[10] YU T X. Large plastic deformation of a circular ring pulled diametrically[J]. Acta Mechanica Sinica, 1979, 11: 88-91.

[11] REID S R, REDDY T Y. Effect of strain hardening on the lateral compression of tubes between rigid plates[J]. International Journal of Solids and Structures, 1978, 14(3): 213-225.

[12] REDDY T Y, REID S R. Lateral compression of tubes and tube-systems with side constraints[J]. International Journal of Mechanical Sciences, 1979, 21(3):187-199.

[13] 赵跃宇, 康厚军, 冯锐,等. 曲线梁研究进展[J]. 力学进展, 2006, 36(2):170-186.

ZHAO Yueyu, KANG Houjun, FENG Rui, et al. Advances of research on curved beams[J]. Advances in Mechanics, 2006, 36(2):170-186.

[14] 童根树. 薄壁曲梁线性和非线性分析理论[M]. 北京：科学出版社, 2004.

[15] RAO S S. Vibration of circular rings and curved beams[M]. New Jersey: John Wiley & Sons Inc., 2007: 393-419.

[16] ABAQUS 6.12 user reference manual[S].2011.