适用于模块化多电平储能变流器的分布式控制策略

王 帅, 荆 龙, 吴学智,2, 李金科, 武 文, 姜久春,2

(1. 北京交通大学国家能源主动配电网技术研发中心, 北京市 100044;2. 北京电动车辆协同创新中心, 北京交通大学, 北京市 100044)

0 引言

储能系统作为交直流电网的中间环节,可以提高电网供电的可靠性,在必要时刻给予电网功率支撑[1-2]。模块化多电平变流器(MMC)作为一种多电平的功率变换装置,与电池结合可以组成新型储能装置,其模块化结构可以使储能电池运行在低电压模式下,具有开关器件电压应力小、谐波小、模块化程度高、输出电压高、易于拓展、可靠性高等优点[3]。目前,模块化多电平储能变流器(MM-ESC)已经引起国内外研究人员的关注,相关研究包括应用于中低压电网[4-5]、电动汽车充电站[6]、新能源发电[7]等领域,未来也适用于柔性直流输电、柔性变电站等应用场合。

MMC一般由上百个子模块组成,实现子模块间的协调控制是MMC控制的关键。目前,MMC大多采用集中式控制架构:由中央控制单元(CCU)完成所有的算法控制、子模块均衡、系统保护与冗余控制。该方法需要将所有的子模块信息、桥臂电流、电网电压电流、直流电压电流以及故障保护信息上传至中央控制器中,再由中央控制器向子模块下发开关脉冲信号,不可避免地需要使用大量的高速输入/输出(I/O)通道以及性能极好的处理器进行运算处理。文献[8]提出增加桥臂控制器的控制系统结构,由主控制器完成功率解耦控制,桥臂控制器完成最近电平逼近调制(NLM)的调制控制,在一定程度上可以有效减少光纤通道数,为缓解通信压力提供了一种解决方案。文献[9]提出了三级控制系统架构,增加了子模块控制器,实现子模块故障信息返回,但并未降低控制系统对通信及运算性能的需求。文献[10]提出将原来由主控制器承担的电容电压均衡控制转移到子模块控制器中,降低了主控制器的控制压力,但仍需主控制器采集各个子模块电压,没有缓解系统内部的通信负担。文献[11]同样采用三级控制,但是提出子模块控制器可以实现脉宽调制(PWM),与此同时,辅助控制器则用来实现全部子模块的互联、子模块均衡、冗余保护等功能。该方法可以将光纤使用量降低,但该控制系统中对中央处理器要求很高,在控制架构设计方面值得进一步进行研究。

在基于MMC实现的电池储能系统中,由于子模块荷电状态(SOC)初始值、子模块系统自身损耗以及系统外部参数不一致等因素,会导致每个子模块连接的电池包SOC出现差异,不利于储能系统容量的充分利用。因此,类似于子模块的均压控制,子模块电池包的SOC均衡控制是必不可少的。文献[12-14]都提出了子模块SOC均衡控制:文献[12-13]通过控制环流实现相间和桥臂间SOC均衡,调节各个子模块的输出工频分量,实现桥臂内SOC均衡;文献[14]则从控制相、桥臂、子模块功率的角度研究了三级SOC策略,同样可以实现控制的目的。但是以上文献都遵循了MMC通用的子模块集中式控制思想:中央控制器采集各子模块电池包信息;依据上述信息,估算电池包SOC;根据不同子模块电池包SOC差异,进行计算处理,得到各子模块SOC均衡补偿量,再将脉冲分发至各子模块。这种方式相对传统MMC的控制,增加了每个子模块的SOC估算处理,在子模块数量很多的情况下,大大加重了中央控制器的负担,整个系统运行性能严重依赖通信和运算能力。

针对以上问题,本文提出了一种基于MM-ESC的新型控制系统架构以及相应的控制策略,在此基础上,分析子模块相间功率差异化特性以及相内功率差异化特性;设置相应下垂曲线,实现子模块相间下垂控制以及相内下垂控制,有效地避免大量信息上传带来的通信和计算压力;同时为了避免调制波发生过调制的现象,利用调制比和实时交流电流确定下垂系数。最后,通过仿真和实验平台对控制架构及算法的有效性进行验证。

1 MM-ESC工作原理

图1为MM-ESC及半桥式储能子模块(ESM)的拓扑结构图。

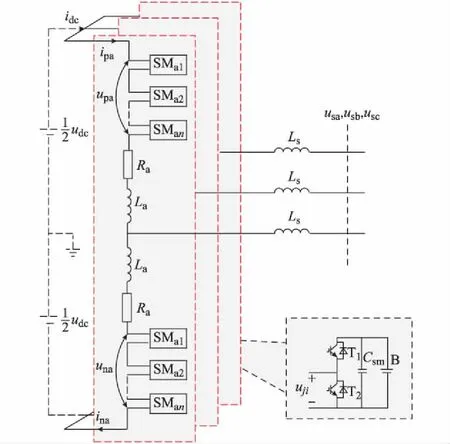
图1 MM-ESC及半桥式储能子模块的拓扑结构Fig.1 Topological structure of MMC-ESC and ESMs with half bridge

图中:Ra为桥臂等效损耗电阻;La为桥臂电感;Ls为交流滤波电感;Csm为储能子模块电容；B表示子模块储能电池;ipj和inj分别为j相上、下桥臂电流;usj为j相交流电压;j取a,b,c。

由于储能电池电压usm随SOC变化较为缓慢,故本文假设储能电池在正常充放电过程中,其电压始终保持为常量。另外,在理想情况下,MM-ESC的相单元参数完全一致,桥臂单元参数完全一致,储能子模块参数完全一致。储能子模块采用电池直接并联在电容两端的连接方式,电容电压被限制为电池电压。通过合理地投切储能子模块,可以在直流侧等效形成虚拟的稳定直流电压udc,即如图1所示的虚线部分。

根据基尔霍夫电压定律,上、下桥臂电压可以表示为:

(1)

设j相环流为icirj,于是j相上、下桥臂电流、环流以及交流电流之间的关系如式(2)所示。

(2)

由于子模块电池电压波动受充放电影响较小,因此桥臂电流中由于充放电形成的二倍频等偶次电流分量很小[14],在本文分析中认为稳态工况时的内部环流为0。故在MM-ESC中并不需要常见的均压控制和环流抑制的闭环控制系统,取而代之的是为避免造成系统储能容量配置浪费的SOC均衡控制。

2 MM-ESC的分布式控制系统

2.1 MM-ESC集中式控制系统

传统MMC普遍采用集中式控制系统,即利用CCU实现对MMC控制。在MM-ESC中,需要在CCU中完成的闭环控制包括:功率解耦控制和SOC均衡控制。功率解耦控制在不同工况实现不同的控制目标:在离网工况下实现对交流电压的控制;在并网工况下实现对交流电流的控制。SOC均衡控制可以分成相间均衡控制和相内均衡控制:相间均衡控制需要保证某相SOC均值跟随其平均参考值;相内均衡控制则保证子模块SOC跟随相平均参考值,该方法可以实时对SOC进行调节,精度很高[15]。

与此同时,为了实现对子模块开关器件动作的控制,还需要加入相关调制策略。在MM-ESC中为保证子模块储能电池充放电一致性,一般采用载波移相的调制策略;采用载波移相PWM(CPS-PWM)的情况下,只有每个储能子模块的载波之间相位发生偏移,每个子模块投切次数相同,也就保证了子模块储能之间的SOC均衡。

采用集中式控制系统架构示意图如附录A图A1所示,ubatjk和ijk分别为j相第k个子模块电池电压和流经电池的电流;PWMjk表示中央运算单元下发至每个子模块的PWM波;k=1,2,…,2n。

采用集中式控制系统控制MMC,需要CCU采集所有子模块储能电池的电压、电流用于估算SOC以及桥臂电流、交流电压/电流等电气量,对CCU的通信量和运算量要求极高。为了降低对中央运算单元运算量的要求,本文提出一种适用于MMC储能变流器的新型分布式控制系统架构。

2.2 MM-ESC分布式控制系统

适用于MM-ESC的分布式控制系统由CCU和子模块控制单元(SCU)两部分组成。CCU中进行电压电流控制,并将各相调制波分发至每个子模块;此时,同相内的子模块接收到的调制波相同,每相仅需要一根与CCU连接的通信线;SCU接收来自CCU的调制波,完成子模块SOC估算和自均衡控制,并根据重组后的调制波进行载波移相调制;此时可以利用时钟脉冲将同相内子模块的本地时钟进行同步,使载波移动相同的相位角度。使用分布式控制系统架构示意图如图2所示,uj表示中央运算单元分发至各相子模块的调制波。

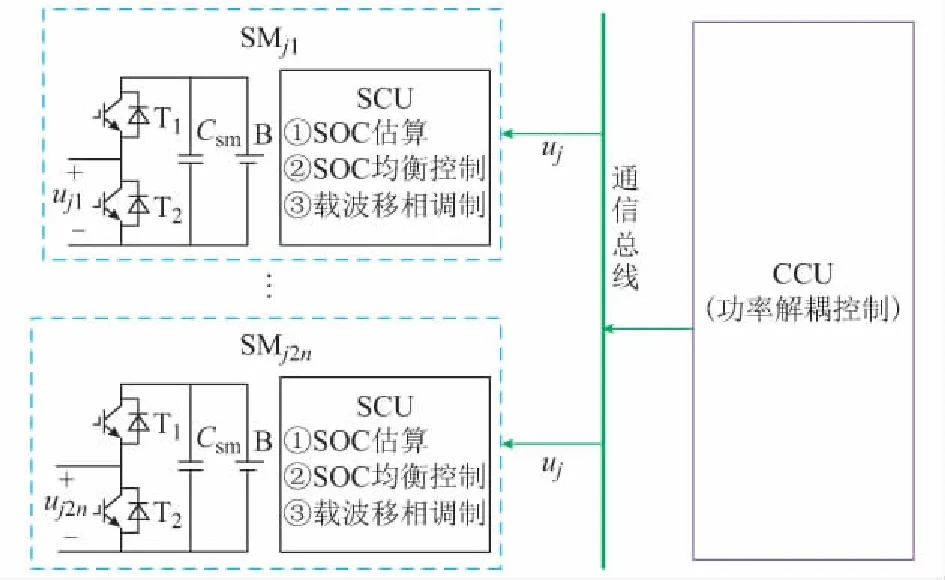
图2 分布式控制系统架构示意图Fig.2 Architecture schematic of distributed control system

两种MM-ESC控制系统架构的通信和计算需求的比较如表1所示,其中n表示一个桥臂内子模块的数量。对比容易发现,采用分布式控制系统在降低系统内部通信量的同时,也可以充分利用SCU的运算能力。

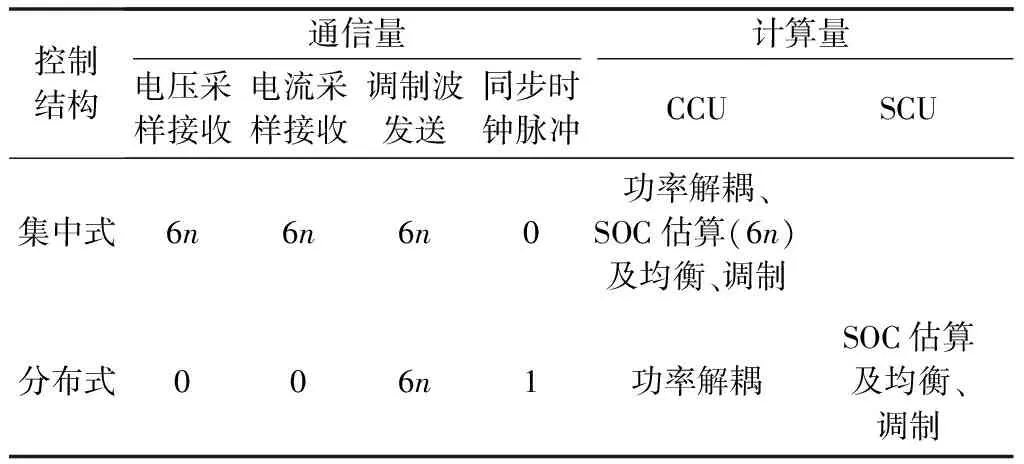
表1 集中式控制系统与分布式控制系统通信量及运算量比较Table 1 Comparison of communication and computation between centralized and distributed control systems

3 适用于MM-ESC的SOC均衡控制

3.1 MMC子模块功率差异控制分析

为了实现MM-ESC不同子模块之间电池SOC的均衡控制,需要让不同子模块输出的功率产生差异,即放电时,控制SOC高的子模块输出功率大,SOC低的子模块输出功率小,充电时则相反,这样不同子模块SOC便会趋于一致。本节将分析子模块传输功率产生差异的机理。

环流作为MMC内部能量传输的载体[16];不同幅值、相位的调制波并由此产生的环流也不相同,会造成各个子模块传输功率的差异,可以利用这种特征进行子模块下垂控制,实现系统能量均匀分配。

稳态工况下的交流电压、电流可以表示为:

(3)

式中:Um为采样得到的交流电压幅值;Im为采样得到的交流电流幅值;ω为采样的电网角频率;φ为交流电压与交流电流相位差。

以a相为例,a相桥臂电流可以表示为:

(4)

忽略桥臂电感、滤波电感等杂散参数的影响,a相上、下桥臂调制波表达式为:

(5)

从电路拓扑结构的角度看,MMC是一个由多个子模块级联形成的电路拓扑,每个子模块都可以等效为一个小型DC/DC变换器;其输入电压是电池电压,经过常规的PWM即可以得到开关器件的脉冲信号;对多个这种小型变换器的协调配合控制,即可以使MMC处于安全稳定运行的状态。因此,将调制波分配至每个子模块即可以得到子模块的等效调制波,如式(6)所示。

(6)

式中:i表示子模块在桥臂中的位置,且1≤i≤n。

每个子模块的输出电压与子模块调制波之间存在如下关系:

(7)

式中:usm为子模块电容电压,在本文中应为子模块电池组电压。

此时,a相子模块功率可以表示为:

(8)

同理,可得b相和c相子模块功率,并表示为:

(9)

为使不同相的子模块功率产生差别,一般可以向各相调制波中叠加直流分量或者三倍频分量,促使各相发生功率流动,但是都会产生基频或者其他频次的功率波动,这种情况是无法避免的。另外,为了加快能量在各相均分,叠加少量的直流分量Ud是合理的解决方式。叠加少量的直流分量Ud后,此时该相调制波可以表示为:

(10)

此时,该相子模块等效调制波可以表示为:

(11)

同式(7),a相子模块等效输出电压则可以表示为:

(12)

假设桥臂等效电阻为Ra,并由此可以得到此时桥臂等效电路如附录A图A2所示。

由于a相调制波叠加的直流分量,此时需要对各相环流进行修正并可以表示为:

(13)

各相桥臂电流也随之修正为:

(14)

因此,同样可以得到叠加直流分量时a相子模块功率,如式(15)所示。

(15)

其中

同理,可以得到b相和c相子模块功率为:

(16)

其中

对比式(8)和式(9)、式(15)和式(16)可知,调制波叠加直流电压分量后,三相子模块功率中增加基频交流分量(A1′,B1′,C1′)和直流分量(A2′,B2′,C2′):基频交流分量对子模块实际功率输出不产生影响,而且这种基频功率波动会以充放电的形式被电池吸收,此时由于电容电压被电池限制为稳定的电池电压,子模块外部特性与传统子模块不同,电容电压波动极小,可忽略不计,因此增加的基频功率不会影响系统外部输出特性;a相直流分量导致a相子模块功率增加,b和c相直流功率分量导致b和c相子模块功率减小,且同相上、下桥臂子模块功率变化相同,实现了相与相子模块功率差异化的目的。

同样,要使相内子模块发生功率差异化,可以向上、下桥臂子模块调制波注入与所在桥臂电流同相位的交流分量,以a相为例,其注入交流分量的算法如式(17)所示。

(17)

式中:k1和k2为向调制波注入与桥臂电流同相位交流分量的比例系数。

a相子模块等效调制波则表征如下:

(18)

a相子模块等效输出电压可以表示为:

(19)

此时,桥臂等效电路如附录A图A3所示。a相环流表达式为:

(20)

其中

此时,a相桥臂电流可以相应的修正为:

(21)

同样可以得到a相子模块功率的表达式为:

(22)

其中

对比式(8)和式(22)可知,调制波叠加交流分量后,a相子模块功率中增加基频、二倍频交流分量(A1″,A2″)和直流分量(A3″,A4″,A5″):基频、二倍频交流分量对实际功率输出不产生影响;直流分量导致a相上、下子模块功率发生不同程度变化,且其变化功率与比例系数k1和k2有关,调整比例系数k1和k2可以促使同相子模块功率不同。

3.2 子模块分布式下垂控制

根据以上关于子模块功率差异化的分析,以及分散控制可减少通信量及运算量的优势,本文使用下垂控制来实现子模块SOC均衡控制,包括相间SOC下垂控制和相内SOC下垂控制。

子模块SOC下垂曲线见附录A图A4所示,其中图A4(a)表示相间SOC下垂曲线,图A4(b)表示相内SOC下垂曲线。S1和S2为不同子模块的SOC;Ud1和Ud2为子模块叠加在调制波中的直流分量;Δu1和Δu2为子模块叠加在调制波中的交流分量;Ud1,Ud2和Δu1,Δu2分别为根据下垂曲线得到的相间、相内下垂补偿量。其中

(23)

(24)

式中:S*为子模块电池包的SOC参考值;kp和ka分别为相间和相内下垂系数。

具体流程框图如附录A图A5所示。其中,Sa1,Sa2和Sb1,Sb2分别为a相和b相子模块的SOC;Uda和Udb分别为a相和b相由于相间下垂控制补偿的直流电压分量之和;Δua1和Δua2为相内下垂控制补偿的交流电压分量。

对子模块调制波直接进行补偿,有一定不足:一方面桥臂电压会发生变化,导致交、直流侧输出产生误差,由于控制外环的存在,可以将误差降至最低,直至忽略；另一方面也会导致某些子模块出现过调制的问题,影响补偿量的因素主要与控制系统选定的下垂系数有关。本文接下来将对下垂系数的选择进行讨论。

3.3 下垂系数选择

采用下垂控制实现SOC均衡存在调制波过调制的问题,因此需要根据调制比和交流电流确定相间下垂系数和相内下垂系数。

根据前文分析,以a相为例,相间及相内下垂补偿量幅值可以表示为:

(25)

式中:S为子模块电池包的SOC。

为避免发生过调制,下垂补偿量与调制比之间的关系应满足:

Ud+Δu+m≤1

(26)

式中:m为调制比。

同时考虑到电池正常工作范围等限制因素,可以得到以下约束条件:

0≤|S-50|≤40

(27)

将式(25)、式(27)代入式(26),因此相间、相内下垂系数的约束条件表示为:

(28)

采用如式(28)所示的约束条件下的下垂系数,可以避免出现过调制的问题。

4 仿真及实验

4.1 仿真算例分析

为了验证本文所提出的控制系统和SOC均衡控制策略,搭建了一台10 kVA三相五电平MM-ESC样机并网工况模型进行仿真验证,采用载波移相调制策略,系统参数选取参照附录B表B1。

附录A图A6为未加入SOC附加下垂控制时SOC变化波形。此时由于子模块开关器件损耗以及开关状态的不一致,从0.5 s开始,SOC出现缓慢的发散现象。除此之外,在交流系统不对称的工况下(负载不平衡或电网不对称),子模块电池组SOC也会发生发散现象。因此加入SOC附加控制尤为关键。

仿真1——相间SOC不同:系统运行初始时,a相子模块SOC均为40%,b相子模块SOC均为60%,c相子模块SOC均为50%;在t1=1.5 s时,施加了本文提出的下垂控制算法。

采用相间下垂控制的三相子模块电池SOC变化波形如图3所示。

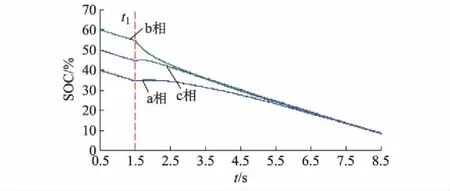
图3 相间下垂控制SOC仿真结果Fig.3 Simulation results of SOC with inter-phase droop control

由图3可以看出,在t1时刻以前由于未加入下垂控制策略,电池处于自由放电状态,三相电池SOC变化始终保持一致;在t1时刻后加入下垂控制的使能信号,由于a相子模块SOC偏低,b相子模块SOC偏高,两相SOC出现向上或向下的趋势,值得一提的是,c相受另外两相叠加调制波的影响,虽然出现一段时间先充电后放电的现象,但是不会影响系统外部输出特性,而且在一段时间后,三相电池SOC保持一致。附录A图A7为三相环流和桥臂电流仿真波形,可以看出,相间SOC不同时,叠加直流调制波分量的方法可以促使系统内部出现直流环流。

仿真2——相内SOC不同:系统运行初始时,a相上桥臂子模块SOC均为60%,a相下桥臂子模块SOC均为40%,b和c相子模块SOC均为50%;在t2=1.5 s时,施加了本文提出的下垂控制算法。

采用相内下垂控制的三相子模块电池SOC变化波形如图4所示,在t2时刻加入下垂控制的使能信号后,a相上、下桥臂电池SOC开始趋于一致,由于其他两相子模块受基频环流影响,出现一定的发散现象,但很快消失,最后所有电池SOC保持一致。附录A图A8为三相环流和桥臂电流仿真波形,可以看出,同相电池组SOC不同时,叠加基频交流调制波分量的方法可以促使系统出现基频交流环流,随SOC相同后,环流中基频分量趋于0。

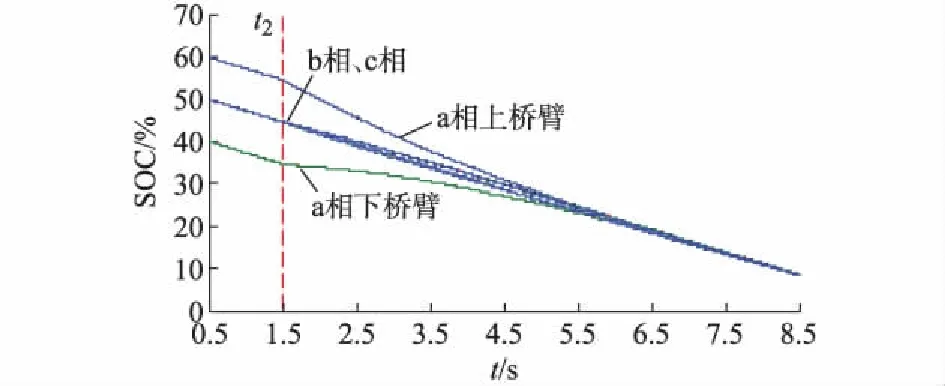
图4 相内下垂控制SOC仿真结果Fig.4 Simulation results of SOC with intra-phase droop control

图3、图4以及附录A图A7、图A8所示的仿真结果表明,本文提出的SOC下垂控制策略能够应用于子模块电池SOC不平衡的情况,可以实现较好的控制效果。

4.2 物理实验验证

物理实验采用了本文提出的控制系统架构,并对所提出的电池SOC均衡控制算法进行了实验验证。实验的研究对象依然采用并网的工作模式。

对于MM-ESC的物理样机,如附录A图A9所示,将SOC均衡算法和载波移相调制策略分布到SCU的复杂可编程逻辑器件(CPLD)中完成。CCU则由数字信号处理器(DSP)和现场可编程门阵列(FPGA)构成,实验所用开关器件采用三菱公司PS21765的智能功率模块(IPM),电池组SOC通过对电压、电流积分的方式进行估算,只用于对电池充放电趋势的统计。MM-CES样机系统参数如附录B表B2所示。

在通信需求方面,通过本文与文献[14]进行对比,当该硬件系统采用集中式控制结构时,下层传感器上传至CCU共有12n+9条数据,包括6n个电池组电压和电流、三相交流电压及6个桥臂电流;下发至每个子模块也有6n个脉冲信息;而分布式控制系统中CCU仅需要从下层采样9份数据信息,包括三相交流电压及6个桥臂电流;下发的通信量也仅仅只有6n个调制波信息,且同相内子模块接收到的调制波信息一致,仅需要外接一条同步时钟脉冲信号,保持各子模块时钟信息相同即可。根据两种控制系统所需通信量的对比,可以发现分布式控制系统对通信需求有较为明显的改善。

从计算压力角度看,同样进行与文献[14]比较,采用集中式控制时,CCU完成了所有的运算;采用分布式控制时,CCU仅进行上层功率解耦控制,下层子模块控制算法在SCU内进行。在中断周期250 μs的配置下,集中式控制系统一个运算周期时间为220 μs,已接近DSP运算极限,而分布式的运算时间不到180 μs,DSP计算能力还有充分的剩余,证明了本文所研究的控制系统可以降低中央运算单元的运算压力。

附录A图A10为稳态下并网电流峰值为4 A时,子模块电容电压和并网电流波形图。由于子模块采用电池组直接并联在子模块电容上,其电容电压始终与电池电压保持一致,电容在一定程度上可以吸收一定的高频电流,而且电池一般要通过电缆连接到储能单元,电缆会有感性分布系数,经过电缆流向电池的电流一般为直流量,对延长电池寿命有一定作用;同时三相并网电流波形保持对称,证明本文研究的分布式控制系统可以应用于MM-ESC系统中。

图5为两种不同情况下三相电池组的SOC均衡曲线。

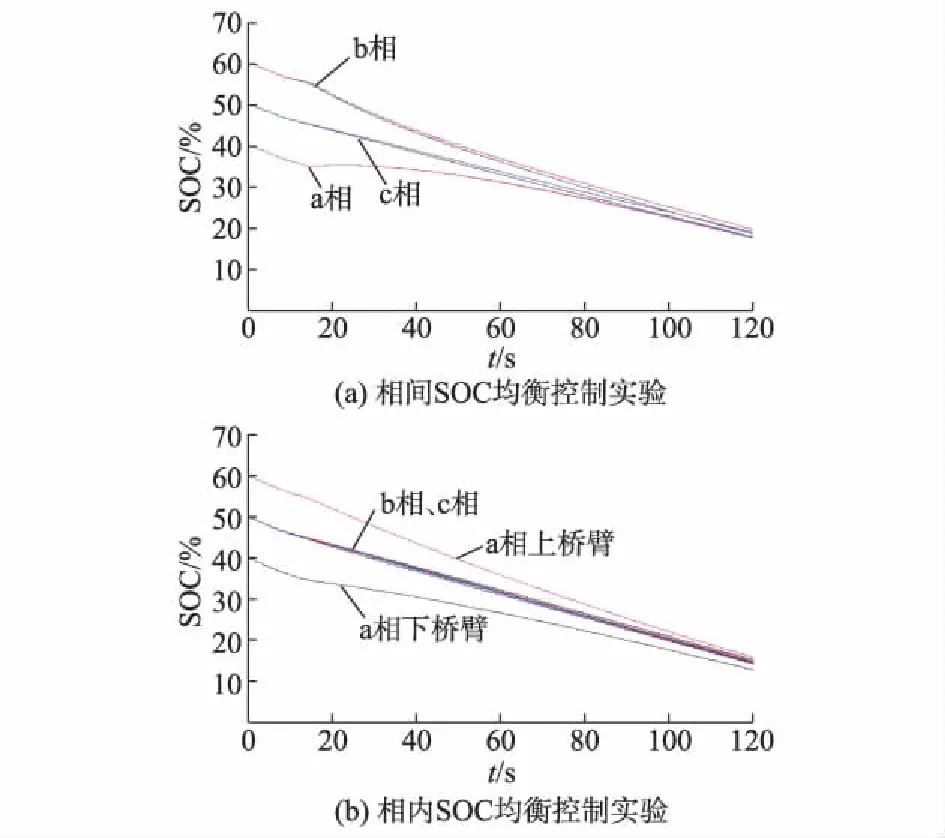
图5 SOC下垂控制实验结果Fig.5 Experiment results of SOC droop control

实验结果表明,本文提出的分布式控制系统架构以及SOC均衡控制策略可以有效实现SOC均衡,与图3、图4以及附录A图A7、图A8所示的仿真结果一致。

5 结语

本文针对MMC储能变流器提出了一种分布式的MMC控制系统架构及SOC下垂均衡控制策略。

1)采用CCU和SCU协同控制的分布式控制架构,CCU负责功率解耦等上层控制,SCU则负责独立子模块的SOC估算、均衡及调制控制,可以有效降低运算和通信压力,提高储能设备的经济性能。

2)对比稳态与叠加直流或交流调制分量后子模块功率变化,提出一种SOC下垂均衡控制策略,可以有效实现SOC均衡,同时还有助于实现子模块的独立控制,避免中央控制器大量信息交换带来的通信及运算压力。

在本文研究中,以采用所有子模块均接入储能电池的MM-ESC为背景,但是电池可能由于故障、SOC过低或过高退出运行,此时的运行状态和控制策略也要相应发生变化,这也是下一步工作的研究方向。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

参考文献

[1] 谭兴国,王辉,张黎,等.微电网复合储能多目标优化配置方法及评价指标[J].电力系统自动化,2014,38(8):7-14.DOI:10.7500/AEPS20130719005.

TAN Xingguo, WANG Hui, ZHANG Li, et al. Multi-objective optimization of hybrid energy storage and assessment indices in microgrid[J]. Automation of Electric Power Systems, 2014, 38(8): 7-14. DOI: 10.7500/AEPS20130719005.

[2] 丁明,陈忠,苏建徽,等.可再生能源发电中的电池储能系统综述[J].电力系统自动化,2013,37(1):19-25.

DING Ming, CHEN Zhong, SU Jianhui, et al. An overview of battery energy storage system for renewable energy generation[J]. Automation of Electric Power Systems, 2013, 37(1): 19-25.

[3] 韩雅帅,徐永海,曹炜,等.带储能系统的级联多电平逆变器的研究进展[J].电测与仪表,2016,53(11):25-31.

HAN Yashuai, XU Yonghai, CAO Wei, et al. Research progress on the applications of CMC with energy storage system[J]. Electrical Measurement & Instrumentation, 2016, 53(11): 25-31.

[4] REN Bin, XU Yonghai, LAN Qiaoqian. A control method for battery energy storage system based on MMC[C]// 2015 IEEE 2nd International Future Energy Electronics Conference (IFEEC), November 1-4, 2015, Taipei, China: 1-6.

[5] 张振华,冯涛.模块化多电平储能单元改善并网风电场稳定性研究[J].四川电力技术,2012,35(1):6-8.

ZHANG Zhenhua, FENG Tao. Study of used modular multilevel storage units to improve the stability of wind farms integrated to grid[J]. Sichuan Electric Power Technology, 2012, 35(1): 6-8.

[6] CICCARELLI F, del PIZZO A, IANNUZZI D, et al. An ultra-fast charging architecture based on modular multilevel converters integrated with energy storage buffers[C]// 2013 8th International Conference and Exhibition on Ecological Vehicles and Renewable Energies (EVER), March 27-30, 2013, Monte Carlo, Monaco: 1-6.

[7] 张卓阳,邓超平,凌志斌,等.基于MMC的光伏发电-电池储能系统控制策略[J].电气传动,2017,47(5):45-49.

ZHANG Zhuoyang, DENG Chaoping, LING Zhibin, et al. Control strategy for a photovoltaic generation-battery energy[J]. Electric Drive, 2017, 47(5): 45-49.

[8] 江道灼,郭捷,周月宾,等.49电平模块化多电平换流器样机设计与实验验证[J].中国电机工程学报,2013,33(27):88-95.

JIANG Daozhuo, GUO Jie, ZHOU Yuebin, et al. Design and experiment of modular multilevel converter prototype with 49-level output voltages[J]. Proceedings of the CSEE, 2013, 33(27): 88-95.

[9] 邵雷.模块化多电平变流器控制系统的研制[D].北京:北京交通大学,2016.

[10] 李建国,杨文博,宋强,等.模块化多电平换流器电容电压的分布式均衡控制方法[J].电力系统自动化,2016,40(17):197-203.DOI:10.7500/AEPS20151022008.

LI Jianguo, YANG Wenbo, SONG Qiang, et al. Distributed balancing control strategy of capacitor voltage for modular multilevel converter[J]. Automation of Electric Power Systems, 2016, 40(17): 197-203. DOI: 10.7500/AEPS20151022008.

[11] 申斐斐,施科研,吕栋,等.一种模块化多电平变流器的控制器架构[J].电源学报,2012(3):13-17.

SHEN Feifei, SHI Keyan, LÜ Dong, et al. Controller architecture of a modular multilevel converter[J]. Journal of Power Supply, 2012(3): 13-17.

[12] 李楠,张磊,马士聪,等.基于模块化多电平换流器的电池储能系统控制策略[J].电力系统自动化,2017,41(9):144-150.DOI:10.7500/AEPS20160707006.

LI Nan, ZHANG Lei, MA Shicong, et al. Control strategy for battery energy storage system based on modular multilevel converters[J]. Automation of Electric Power Systems, 2017, 41(9): 144-150. DOI: 10.7500/AEPS20160707006.

[13] GAO F, ZHANG L, ZHOU Q, et al. State-of-charge balancing control strategy of battery energy storage system based on modular multilevel converter[C]// 2014 IEEE Energy Conversion Congress and Exposition (ECCE), September 14-18, 2014, Pittsburgh, PA, USA: 14-18.

[14] 郭龙,梁晖,张维戈.基于模块化多电平变流器的电池储能系统荷电状态均衡控制策略[J].电网技术,2017,41(8):2688-2697.

GUO Long, LIANG Hui, ZHANG Weige. State-of-charge balancing control strategy for battery energy storage system based on modular multilevel converter[J]. Power System Technology, 2017, 41(8): 2688-2697.

[15] 王帅,荆龙,吴学智,等.基于MMC的储能系统SOC均衡控制[J].电力电子技术,2016,50(11):60-62.

WANG Shuai, JING Long, WU Xuezhi, et al. SOC balance control strategy of MMC energy storage converter[J]. Power Electronics, 2016, 50(11): 60-62.

[16] 周月宾,江道灼,郭捷,等.模块化多电平换流器子模块电容电压波动与内部环流分析[J].中国电机工程学报,2012,32(24):8-14.

ZHOU Yuebin, JIANG Daozhuo, GUO Jie, et al. Analysis of sub-module capacitor voltage ripples and circulating currents in modular multilevel converters[J]. Proceedings of the CSEE, 2012, 32(24): 8-14.